基于灵敏度分析的车门尺寸和拓扑优化*

胡启国，邓维敏，罗天洪

(重庆交通大学 机电与汽车工程学院，重庆 400074)



基于灵敏度分析的车门尺寸和拓扑优化*

胡启国，邓维敏，罗天洪

(重庆交通大学 机电与汽车工程学院，重庆 400074)

摘要：为了改善微型车X30的车门在使用过程中振动过大这一问题，利用Hypermesh建立该车车门的有限元模型，并对其进行模态分析。分析结果发现车门的一阶频率偏低，容易与白车身一阶弯曲频率发生共振。因此，基于灵敏度分析方法结合尺寸优化和拓扑优化方法对车门进行以提升车门一阶模态频率为目标的优化设计。首先，对车门各零部件进行质量灵敏度和一阶模态频率灵敏度分析，并定义相对灵敏度值；然后，根据相对灵敏度值结果选择合适的设计变量进行部件厚度的尺寸优化设计；最后，基于变密度法对相对灵敏值最大的部件进行拓扑优化，根据优化结果对该部件有限元模型进行修改。结果表明，在车门质量减少4.5%的情况下，车门一阶模态频率提高8.9%，有效地改善了车门的振动情况。

关键词：车门；模态分析；灵敏度分析；尺寸优化；拓扑优化

0引言

车门是车身上一个重要的覆盖件，主要由壳体、附件及内饰板等组成。其中，壳体主要是由外板和内板等部件通过粘胶、焊接、包边等工艺连接而成[1]。汽车在行驶过程中会受到各种外界激励的影响，如果车门与某一频率发生共振，就可能会对车门自身结构产生影响。基于此，本文以微型车车门为研究对象，首先对其进行模态分析，然后通过灵敏度分析选择合适的设计变量进行尺寸和拓扑的双重优化，从而改善车门的一阶频率，为车门轻量化及车门动态特性研究提供一定的参考。

1车门有限元模型的建立

1.1模型的导入和清理

将原始的车门CATIA模型通过Iges格式导入Hypermesh中[2]。注意观察模型是否合理，对于常出现的比如缺面、多余曲面、缝隙等错误进行修改。然后对三维模型进行中面的抽取。后期的网格划分均在中面上进行，此时的模型看不到厚度，厚度将在网格划分完毕后对其赋予属性时设置。抽取中面后的几何模型如图1、图2所示。

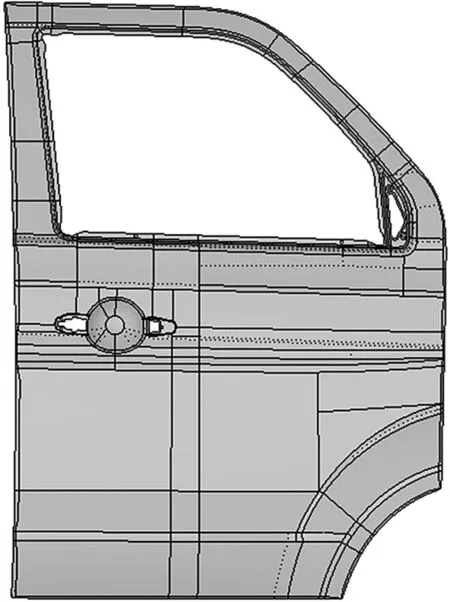
图1　车门外板

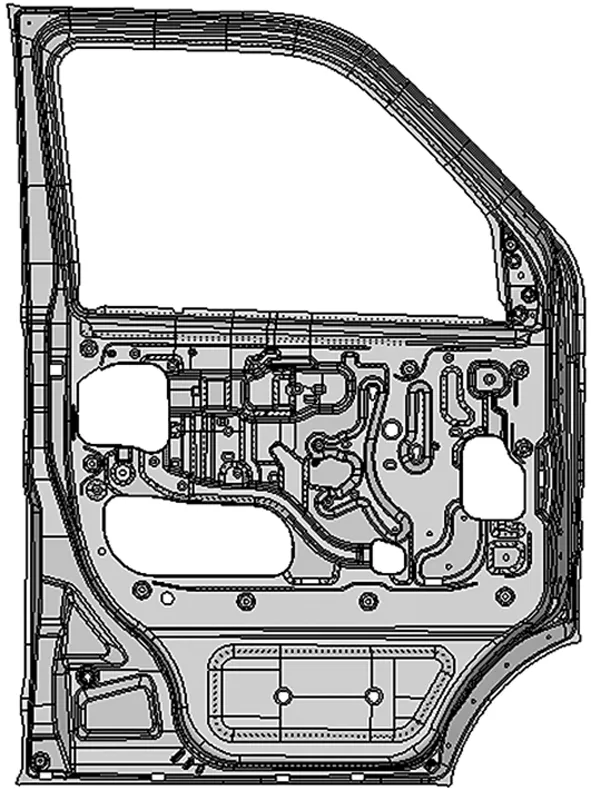
图2　车门内板

为了使有限元分析的效率更高，有必要对车门模型进行简化。本文做了以下规定：忽略R3以下的倒角；为了使孔洞的CAE外形更好，使用washer功能对孔洞(特别是螺栓孔)进行处理，将其周围的网格优化为正N边形结构[3]；R4以上的孔至少6个节点模拟且不能出现奇数节点。

1.2网格划分

车门模型中部件大部分为钣金件，少部分如防撞梁是长杆件[4]。因此使用壳shell单元来对钣金件进行网格划分。网格的大小会影响分析的效率和精确度。网格单元越小，有限元模型就越贴近实际，但同时会影响计算的效率。因此，选择既能表现实际的模型又有效率的单元尺寸很重要。本文选择10×10mm的四边形单元。车门的焊点采用reb2单元进行模拟。车门外板和内板采用包边的方式进行连接，包边仅有一层单元，厚度为T=2T1+T2。T1为外板厚度，T2为内板厚度。车门使用同一种材料，材料的弹性模量为2.0E+05MPa，泊松比为0.36，密度7.9e-09t/mm3。

表1　主要部件尺寸

网格质量的检查很重要。在很多分析中，往往由于网格质量的不过关而导致计算的终止或影响计算结果的准确性[5]。网格划分完成后以表2所示标准进行质量检查。质量检查合格后方能进行模态分析。

表2　车门网格划分质量标准

质量检查合格以后，得到车门最终有限元模型如图3所示。模型包含：69343个节点，51785个四边形单元，2161个三角形单元，15个五面体单元，386个六面体单元；质量18.31kg。

图3　车门有限元模型

2模态结果与分析

2.1模态分析

通过Optistruct求解器对车门进行自由模态分析[6]。因为车门的刚体模态频率极小，在求解过程中基本可以忽略。前四阶计算结果如表3、振型如图4～图8所示 。

图4　一阶模态振型图

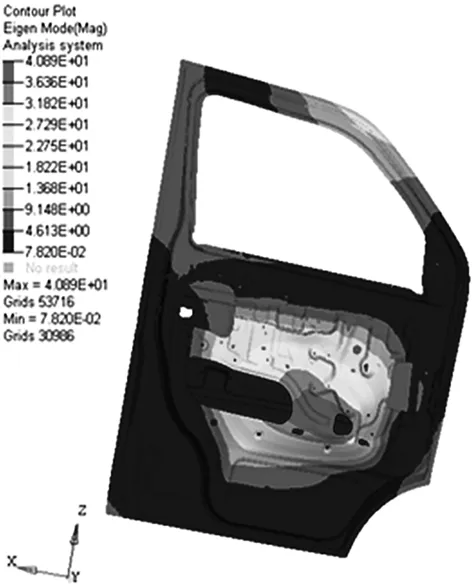
图5　车门二阶模态振型图

图6　三阶模态振型图

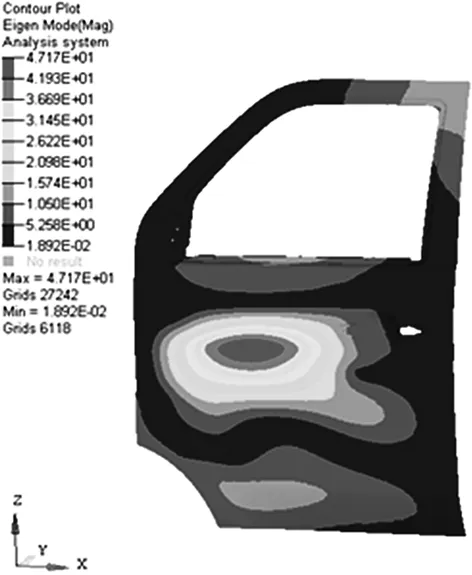
图7　四阶模态振型图

模态阶数固有频率/Hz振型描述135.63外板局部振动239.93内板局部振动346.91一阶扭转457.69一阶弯曲561.00二阶弯曲

2.2模态分析评价

一阶：固有频率为35.63Hz，车门此时的振型表现为车门外板的局部振动，位置处于车门的中下部。二阶：固有频率为39.93Hz，车门此时的振型表现为车门内板的局部振动，特征值最大的位置处于内板中较大的音响安装孔附近。三阶：固有频率为46.91Hz，车门此时的振型表现为车门外板的局部振动，位置处于车门的中下部，最大的特征值出现在车窗框处。同时车门也表现出整体结构的扭转变形。四阶：固有频率为57.69Hz，此时的振型表现为车门外板的局部振动，位置处于腰线附近；四阶模态同时还包括整体的弯曲变形。五阶：固有频率为61.00Hz，可以观察到车门此时的振型表现为整体的弯曲变形。最大的特征值处在窗框角处。

白车身前4阶频率分别为21.8Hz，25.5 Hz，30.5 Hz，35.4 Hz。因此，车门一阶模态频率容易与白车身第四阶频率发生共振。所以需要提高车门的一阶模态频率以避免共振。

3车门部件灵敏度计算

3.1灵敏度理论

在自由模态分析中，系统的振动方程可表示为：

(1)

式(1)对设计变量xi求偏导数得：

(2)

整理后：

(3)

式(3)中，ω=2πf，因此系统的固有频率对设计变量xi的灵敏度表示为：

3.2灵敏度分析

灵敏度分析可以确定优化过程中对目标性能响应最为灵敏的结构性能参数，从而可根据灵敏度分析结果选择关键部件作为优化设计变量。

本文以车门各部件的厚度作为设计变量，一阶频率作为响应，车门质量最小为目标，通过分析可以得到各部件的质量灵敏度和一阶频率灵敏度[7]，提交OptiStruct求解器求解，计算结果如表4所示。

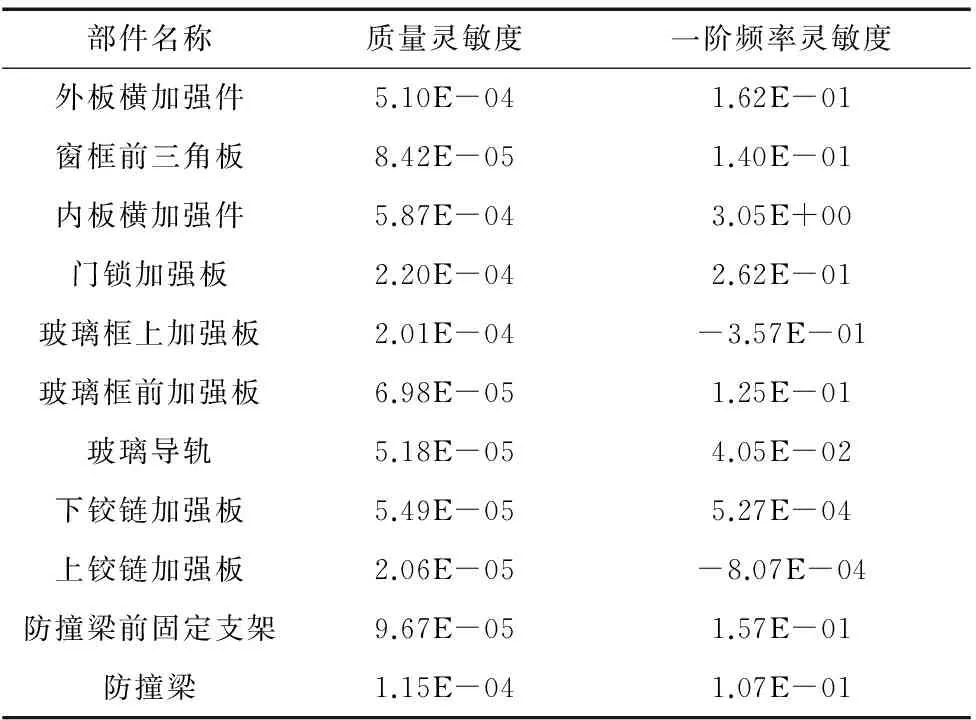
表4　部分车门部件灵敏度分析结果

由表4中可知，各部件的质量灵敏度值均为正值，这说明所有部件厚度增加，整个车门的质量也会增加。其中，内板和外板的数值较其他部件更大，这是因为这2个部件是车门中质量最大的两个部件，和其他部件相比，在厚度均增加1mm的情况下，内板和外板更能引起车门质量的增加。一阶频率灵敏度值有正有负，说明并不是只要增加部件厚度就能引起车门一阶频率的提升。

为了衡量各部件厚度变化对各工况的灵敏度的影响，定义衡量指标：LF=F/M。其中：M是车门质量对部件厚度的灵敏度，F是一阶频率对部件厚度的灵敏度。指标L值反映了一阶频率对车门质量的灵敏度。当L≤0时，说明增加该部件厚度反而会使响应值降低。因此在选择优化变量时应舍弃。当L>0时，说明在增加相同质量的情况下，厚度的改变对响应值的影响更大。图9为各部件的LF值。

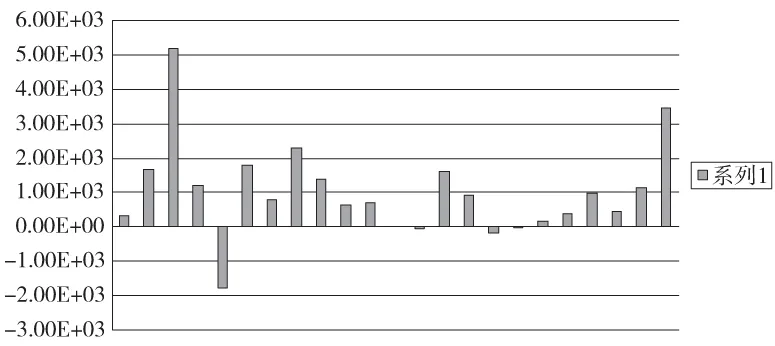
图8　各部件的LF值

由图8可知，门锁加强板、内板、铰链加强板、下铰链安装支架、下铰链加强板、防撞梁前固定支架、防撞梁加强横梁、中部加强板、横梁前支架、横梁后支架、外板等11个板件的数值均为正且数值较其他部件更大，故可选为尺寸优化设计的设计变量。

4车门模态优化设计

4.1优化方法介绍

在车门尺寸优化中，各部件的结构形状和拓扑结构不发生变化，仅通过优化改变结构的单元属性如截面面积、板的厚度等变量。本文以灵敏度分析选择的11个部件的厚度ti(i=1,2,…,n)作为优化设计变量，则优化模型可表示为：

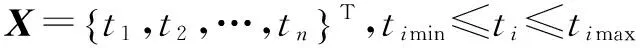
使F(X)→max(ormin)

满足Smin≤S≤Smax,gmin≤g≤gmax

其中，X为设计变量向量；n为设计变量的个数；timin和timax分别为部件厚度的下限和上限；F(X)为目标函数；Smax、Smin分别为结构模态约束上下限值gmax、gmin分别为结构刚度约束上下限值。尺寸优化过程就是一个不断迭代的过程，在满足约束条件下，使目标函数的解达到最优。

拓扑优化模型采用变密度法，通过引入一种假想的相对密度在0-1之间的材料，并假定相对密度与材料属性弹性模量之间的关系，通过优化结果将密度小的区域材料去掉，密度大的区域材料加强的方式来寻求材料的最佳布局。计算模型可表示为：

使F(X)→max(ormin)

满足gj(X)≤0，j=1,2，…，m

hk(X)=0，k=1,2，…，p

其中：X为设计变量；n为设计变量的个数；F(X)为目标函数；gj(X)(j=1,2，…，m) 为不等式约束函数；hk(X)(k=1,2，…，p)为等式约束函数。

4.2尺寸优化结果及分析

设置好相应的约束与响应条件，提交OptiStruct求解器进行计算[8]。经过6次迭代计算，目标函数收敛，优化完成，优化结果如表5所示。

由表5可知，优化后质量降低0.96kg，一阶频率提高2.08Hz。前五阶频率分别为：37.71Hz、42.99 Hz 、45.73 Hz、62.89 Hz、72.48 Hz。由分析结果可知，根据灵敏度分析结合尺寸优化方法能在车门模态频率不下降的情况下有效地减轻车门的质量。但一般轿车一阶频率的平均值为38Hz[9]，所以该车门的一阶频率仍较低，后续需要对其进行进一步的研究和分析。

表5　优化结果

4.3拓扑优化

针对尺寸优化后一阶频率仍较小的情况，采取如下策略：根据表5的一阶频率灵敏度结果选择对车门一阶频率影响最大的部件(即：内板横加强板，有限元模型如图9所示)进行拓扑优化。

图9　内板横加强板的原始有限元模型

文中以一阶模态频率最大化为目标函数，车门质量最小化作为约束条件。优化结果如图10所示，红色部分代表此处密度趋于1.0，表示该区域材料需要加固；蓝色部分代表密度趋于0.0，表示该区域材料可以删除。

图10　内板横加强板拓扑优化后的有限元模型

基于获得的拓扑优化结果，对部件716的有限元模型进行修改，在密度趋于1.0的区域增加了许多加强筋。对修改后的模型进行模态分析，一阶模态频率增加至38.71 Hz，质量增加0.15kg。

5结论

研究结果表明，对车门的自由模态进行分析，根据各部件对车门质量和模态频率的灵敏度确定需要优化的部件。结合尺寸和拓扑优化设计方法对车门一阶模态频率进行优化设计，实现了车门一阶频率提高了8.9%，车门质量减少4.5%。

综合本文研究可得，基于部件厚度的灵敏度方法选择合适的设计变量进行尺寸和拓扑优化能更高效率地实现车门模态性能和轻量化的优化要求。

[参考文献]

[1] 黄天泽，黄金陵．汽车车身结构与设计[M]．北京：机械工业出版社，1997．

[2] 宋海生，史文库，龙岩,等．整车模态分析中焊点模拟方法的研究[J]．汽车工程，2011，33(11)：920-923．

[3] 张坤，丁晓红，倪维宇,等．汽车座椅骨架构件布局设计方法[J]．工程技术学报，2015，22(2)，166-171．

[4] 解跃青，雷雨成．汽车前车门结构性能的计算机辅助分析与研究[J]．机械强度，2002，24(4)：539-542.

[5] 刘云刚．基于刚度和耐撞性的车门结构轻量化设计研究[D]．广州:华南理工大学,2013．

[6] 周鋐，刘浩，范昊天．基于模态和刚度的车门优化研究[J]．制造业自动化，2014，36(8)：93-96．

[7] S Kodiyalam, R J Yang,L Gu,et al. Multidisciplinary design optimization of a vehicle system in ascalable, high performance computing environment[J] . Structural and Multidisciplinary Optimization , 2004 , 26 (3-4): 256-263 .

[8] 朱茂桃，钱洋，顾娅欣，等．基于Kriging模型的车门刚度和模态分析[J]．汽车工程，2013，35(11)：1047-1050．

[9] 王宏雁,徐少英．车门的轻量化设计[J]．汽车工程，2004，26(3)：349-353．

(编辑赵蓉)

Size and Topology Optimization of Car Door Based on Sensitivity Analysis

HU Qi-guo, DENG Wei-min, LUO Tian-hong

(College of Mechatroics and Automobile Engineering,Chongqing Jiaotong University, Chongqing 400074,China)

Abstract：In order to improve the vibration problem of the micro car X30 in the using process, the finite element model of the door was built in Hypermesh and modal analysis was carried on the door. The analysis results showed that the first-order frequency of the door was low, which would easily resonate with first-order bending of the body. So, on the basis of the sensitivity analysis method combined with size optimization and topology optimization method to improve the first-order modal frequency of the door.First, the mass sensitivity and first order modal frequency sensitivity analysis were carried on the parts of the door, and defined the relative sensitivity values of every part. Then according to the relative sensitivity value to select appropriate components as the design variables of the size optimization design. Finally, the topology optimization that based on variable density method was used on one of the part of the door, which had the highest relative value. According to the result to modify the finite element model of the component. The results showed that under the premise of door quality decrease by 4.5%,the first order modal frequency of the door was increased 8.9%. This method effectively improves the vibration performance of the door.

Key words：vehicle door; modal analysis; sensitivity analysis; size optimization; topology optimization

文章编号：1001-2265(2016)05-0004-05

DOI:10.13462/j.cnki.mmtamt.2016.05.002

收稿日期：2015-06-10

*基金项目：国家自然科学基金项目(51275537)

作者简介：胡启国(1967—)，男，重庆人，重庆交通大学教授，博士，研究方向为振动与噪声，机械可靠性，(E-mail)swpihqg@163.com。

中图分类号：TH162;TG506

文献标识码：A