基于不同收缩曲线的圆射流流场拟序结构分析*

罗　静，李丙乾，李　健

(重庆理工大学 a.机械工程学院；b.汽车零部件先进制造技术教育部重点实验室，重庆　400054)



基于不同收缩曲线的圆射流流场拟序结构分析*

罗静a,b，李丙乾a,b，李健a,b

(重庆理工大学 a.机械工程学院；b.汽车零部件先进制造技术教育部重点实验室，重庆400054)

摘要：为了分析不同的收缩曲线对喷嘴外部流场中流场结构的影响，利用大涡模拟方法，对具有正弦曲线、双三次曲线、维多辛斯基曲线的收缩段的外部流场进行了数值模拟，通过对比分析，正弦曲线喷嘴出口处的速度分布、湍流强度分布均优于其余两种曲线，并且其初始剪切层较薄，外部流场中涡环的卷起、配对现象明显，正弦收缩曲线的收缩段的外部流场的模拟结果与实验图像结果基本相符。

关键词：大涡模拟；拟序结构；收缩曲线；数值分析

0引言

自由射流的能量传递、动量运输、流体的卷吸和混掺等过程与喷嘴出口处的存在的速度间断面所产生的自由剪切层中涡结构的发展和演变过程密切相关。由于射入静止环境中的流体与周围环境流体之间存在速度间断面，且此间断面是不稳定的，一旦受到扰动将失去稳定，进而产生漩涡，这些漩涡通过分裂、变形、卷吸和合并配对等过程，除形成大量的随机运动湍动涡体外，还存在着一部分有序的大尺度涡结构，即大涡拟序结构。通过研究发现，这些大尺度的涡拟序结构与剪切层的厚度有关，而且具有一定的频率，即大涡频率[1]。流程中通过涡结构对周围流体的卷吸、掺混等作用，极大的促进了射流与周围流体的混合。

随着流体主动控制技术的发展，人们对通过控制流场中的大涡拟序结构来控制流场的流动特性进行了大量的研究，取得了很好的成果。为了进一步更好地对圆射流的流动特性进行探讨，设计了一套射流实验装置，本装置在于探讨利用周向高频微射流控制主射流的相关流动特性的研究。图1为射流试验台结构图。

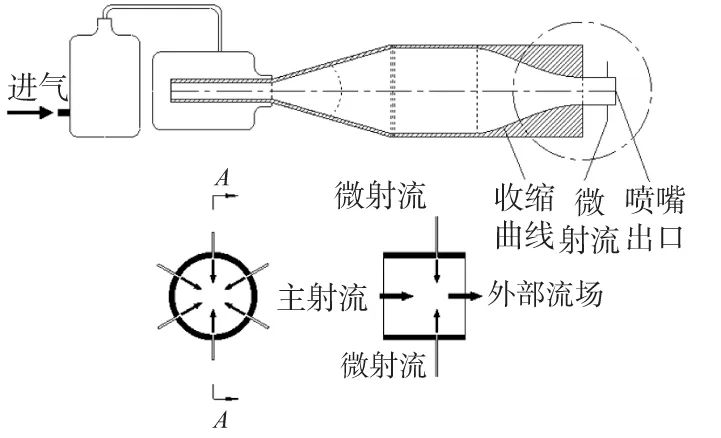
图1　射流试验台结构图

本实验台的实验原理即利用高频微射流对主射流初始流动状态进行控制，进而控制射流流场中的流动特性，包括衰减、卷吸与混合等。因此要求自由主射流外部流场具有明显的大涡拟序结构，通过MI等人的研究表明，射流的大涡拟序结构与射流喷嘴出口处流动的初始流动状态相关，湍流度过大，初始剪切层过厚都会影响外部流场中大涡的拟序结构，而喷嘴出口处的初始流动状态与收缩段收敛曲线的选择有关[1]。

文献[2-5]对各种已知的收缩曲线进行了详细的数值模拟与分析，着重分析了它们出口处气体流动的均匀性和稳定性等特性，但是没有分析它们对外部流场的拟序结构的影响，因此下面对双三次曲线、维多辛斯基曲线、正弦曲线三种收缩曲线进行数值模拟和分析，讨论不同曲线喷嘴出口处速度分布、湍流度分布以及剪切层厚度和外部流场的大涡结构。

1试验台收缩曲线结构和模型

1.1收缩曲线

收缩曲线可用图2来表示，图中： R1为进口半径;R2为出口半径；L为收缩段长度。

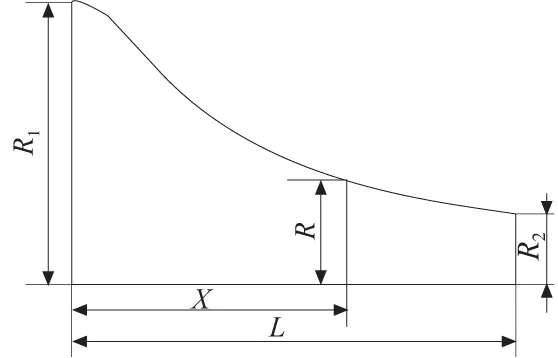
图2　收缩曲线

三种收缩曲线的函数表达式如下所示：

(1)双三次曲线

(2)正弦曲线

(3)维多辛斯基曲线

图3是绘制的三种收缩曲线轮廓图。从图中可以看出，在这三种曲线中，维多辛斯基曲线在进口段部分收缩很快，但是在出口段则很平缓，由于进口收缩过快，在出口处可能出现剪切层过厚，而双三次曲线和正弦曲线则在进口处收缩都较平缓，并且双三次曲线在进口段比正弦曲线平缓，而正弦曲线在出口段比双三次曲线平缓一些。

1.2数值计算模型

图4为数值分析的计算模型和网格，左边部分为收缩段，采用速度进口，速度均匀分布，速度为0.18m/s，右边为外部流场区域，四周设置为压力入口边界条件，出口设置为压力远场出口，表压力设置为零，其他部分均采用无滑移固体边界条件。外部流场尺寸为直径为10D，高10D的圆柱(D为射流喷嘴出口直径)，网格采用六面体网格，网格总数为440万。

图4　计算模型和网格划分

1.3数值计算方法

采用大涡模拟(LES)的方法对流场进行数值计算，首先对不可压缩流体N-S方程进行滤波，采用了盒式滤波器，滤波函数为：

其中：Δxi为i方向的网格尺度。滤波以后的N-S方程为：

对于亚格子模型，本文采用动力模型来模拟亚格子尺度效应。这种模型可以根据当时当地的湍流动力学性质来确定涡粘性模型中的常数，减少了亚格子模型中的人为因素。

计算过程中，对流项采用二阶迎风格式，扩散项的离散采用二阶精度的中心差分格式，压力方程采用中心差分格式离散。

2计算结果与分析

2.1喷嘴出口速度、湍流度分布

喷嘴出口处射流的初始流动状态，主要是指射流出口速度的均匀度、平均湍流度和剪切层的分布等，这些因素对射流近场的大涡拟序结构的产生有很大的影响。

图5为三种收缩曲线在喷嘴出口处的速度沿径向的分布情况。对数据进行无量纲化处理，其中U0为射流喷嘴截面中心处速度,UY为喷嘴出口沿Y轴方向上的速度值。横坐标以喷嘴半径R进行无量纲化。

图5　三种不同收缩曲线出口处速度分布

从图中三种收缩曲线喷嘴出口处速度分布对比情况可得到，正弦曲线出口的速度分布最均匀，其次是双三次曲线，均匀度最差的是维多辛斯基曲线。

图6为三种收缩曲线喷嘴出口处湍流度沿径向的分布情况，横坐标同样以喷嘴半径R进行无量纲化。三种收缩曲线喷嘴出口中心处的湍流强度均在0.02%左右，但是沿径向分布却截然不同，就湍流强度在0.02%的分布范围而言，以正弦曲线为收缩段的分布范围为-0.8≤Y/R≤0.8，而以双三次曲线为收缩段的分布范围为-0.6≤Y/R≤0.6，分布最差的为以维多辛斯基曲线为收缩段的情况，其分布范围为-0.5≤Y/R≤0.5。

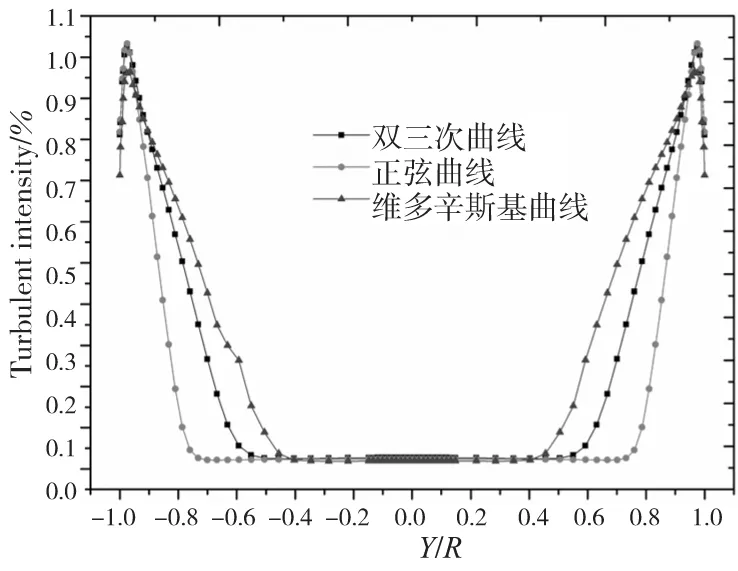
图6　三种不同收缩曲线出口处湍流强度分布

通过对三种收缩曲线喷嘴出口处速度和湍流强度的分布情况的分析，可以得到，正弦曲线相比其他两种曲线，速度的均匀性较好，初始剪切层较薄，湍流强度的分布情况较好。

2.2不同收缩曲线喷嘴射流近场的湍流结构

图7 为三种不同收缩曲线喷嘴流场瞬时涡量图，图中，横坐标与纵坐标均以喷嘴直径D进行无量纲化。三种收缩曲线喷嘴的外部流场中，正弦曲线的剪切层较薄，而维多辛斯基曲线的剪切层最厚。在模拟计算中，采用三种不同的收缩喷嘴时，流场中均出现了大尺度的涡结构，正弦曲线的流场涡结构最为明显，而维多辛斯基曲线的流场涡结构不是很明显。

图8为三种收缩曲线外部流场区域的瞬时涡量图，图8a为正弦曲线喷嘴外部流场的瞬时涡量图，从图中可以清楚地观察到涡环的卷起和配对的现象，涡环的卷起位置约在X/D=3处。双三次曲线喷嘴外部流场涡环卷起发生在X/D=3.5处，与正弦曲线外部流场的涡结构相比，比较混乱，而且观察不到涡环的配对等现象。维多辛斯基曲线喷嘴外部流场中基本观察不到明显的涡环的卷起现象，而且大尺度的结构发生在X/D=4.5处。

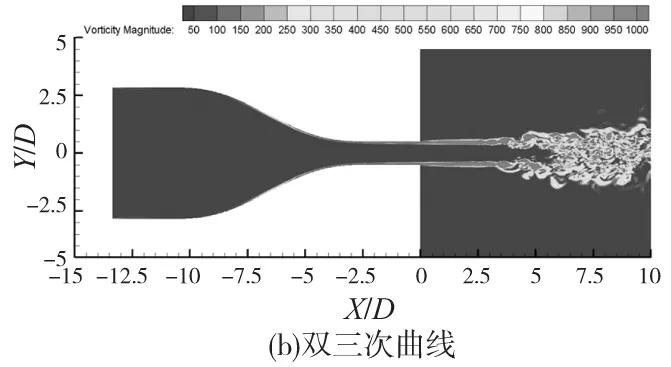
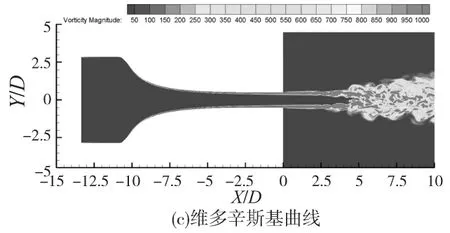
图7　三种收缩曲线喷嘴流场瞬时涡量图

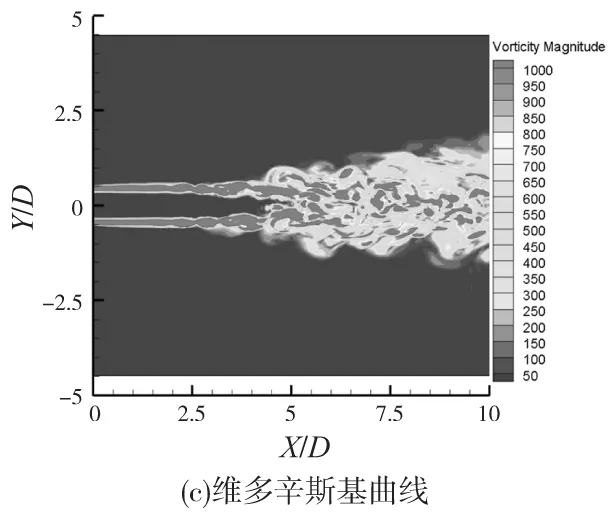
图8　三种收缩曲线外部流场瞬时涡量图

图9为采用正弦曲线作为收敛段曲线的实验装置外部流场流动显示结果，通过计算机数值模拟的得到的正弦曲线外部流场中涡环的卷起、配对现象与实验图像显示结果基本相符。

图9　正弦曲线外部流场实验结果

3结论

为了给一套射流装置选取合适的收缩段的收缩曲线，以便更好的利用该装置对圆射流外部流场中的大涡拟序结构进行研究，本文利用大涡模拟方法，对具有正弦曲线、双三次曲线、维多辛斯基曲线的收缩段的外部流场进行了数值模拟。通过对比分析，正弦曲线喷嘴出口处的速度分布、湍流强度分布均优于其余两种曲线，并且正弦曲线的外部流场中初始剪切层较薄，涡环的卷起、配对现象明显，符合实验装置的设计要求，可以利用该实验装置进一步对射流进行相关的研究。

[参考文献]

[1] 罗静，李健，申跃，等.高频微射流试验台的设计[J]，组合机床与自动化加工技术，2015(5):134-136.

[2] 王帅，刘小康，陆龙生. 直流式低速风洞收缩段收缩曲线的仿真分析[J]，机床与液压，2012,40(11):100-104.

[3] 宋立，田瑞，刘占峰，等. 基于CFD的低速风洞出口实验段流场速度均匀性分析研究[J]. 内蒙古农业大学学报，2011,32(2):199-201.

[4] 吴宗成，陈宴清，万曦. 水洞收缩段的数值模拟及优选[J]. 北京航空航天大学学报，2008, 24(3):315-318.

[5] 侯志勇，王连泽，周建和，等. 低湍流度风洞设计再探讨[J]. 实验流体力学，2011，325(1):92-96.

[6] DU Cheng , MI Jiachun , ZHOU Yu . Mini-Jet Controlled Turbulent Round Air Jet [J]. CHIN.PHYS.LETT.2011,28(12):124703.1-4.

[7] J Mi, G J Nathan . Statistical properties of turbulent free jets issuing from nine differently-shaped nozzles[J]. Flow Turbulence Combust，2010，84:583-606.

[8] 史万里，葛宁. 脉冲横向射流的大涡模拟[J]. 航空动力学报，2013，28(1):143-150.

[9] 赵平辉，叶桃红，朱旻天,等.圆形射流湍流场的大涡模拟研究[J].工程热物理学报，2012,33(3):529-532.

[10] 范全林，王希麟，张会强,等. 圆湍射流拟序结构研究进展[J]. 力学进展，2002，32(1):109-118.

[11] 李家军，王强.脉冲射流强化喷流混合的数值模拟[J].北京航空航天大学学报，2009，35(12):1491-1494.

(编辑赵蓉)

The Analysis of Coherent Structure in Round Jet Based on Different Contraction Curve in Contraction Section

LUO Jinga,b, LI Bing-qiana,b, LI Jiana,b

(a. School of Mechanical Engineering;b.Key Laboratory of Advanced Manufacturing Technology for Automobile Parts, Ministry of Education, Chongqing University of Technology ,Chongqing 400054,China)

Abstract：In order to analysis the effect of different contraction curve on the external flow field of round jet, a numerical simulation, large eddy simulation, is conducted to study the contractive section of external flow field with sine curve, bicubic curve, Witozinsky curve contractive nozzle. Based on the comparison, the nozzle with sine curve is superior to the other two nozzles, with bicubic curve or Witozinsky curve respectively, in the distribution of the velocity and turbulence intensity in outlet. The initial shear layer is thin in the external flow field, and the vortex ring rolled and paired is obviously observed in this field. In addition, the result of the simulation of the external flow field with sine contraction curve nozzle is almost in accordance with the image get from the experiment.

Key words：large eddy simulation; coherent structure;contraction curve; numerical simulation

文章编号：1001-2265(2016)05-0025-04

DOI:10.13462/j.cnki.mmtamt.2016.05.007

收稿日期：2015-07-14；修回日期：2015-08-11

*基金项目：国家自然科学基金(51275550)

作者简介：罗静(1974—)，女，重庆人，重庆理工大学教授，硕士，研究方向为集成制造技术及装备，(E-mail)luojing@cqut.edu.cn。

中图分类号：TH166;TG506

文献标识码：A