基于加权优化的机器人逆向运动学求解*
2016-06-16王光道刘荫忠孙维堂
王光道,刘荫忠,孙维堂
(1.中国科学院大学,北京 100049;2.中国科学院 沈阳计算技术研究所,沈阳 110168)
基于加权优化的机器人逆向运动学求解*
王光道1,2,刘荫忠2,孙维堂2
(1.中国科学院大学,北京100049;2.中国科学院 沈阳计算技术研究所,沈阳110168)
摘要:逆向运动学求解是实现机器人运动控制的关键问题之一。如何快速准确地确定最优解一直成为国内外研究的热点。为此,对MOTOMAN-MH6机器人逆向运动学的优化问题进行了研究。利用D-H矩阵建立了机器人运动学模型,分析了代数解析法的求解过程,得到了多重完整逆解。结合机器人的结构特点和实际需求,提出了加权“最短行程”准则,给定了权重函数的表达式,确定了逆向运动学的最优解。最后,通过机器人三维仿真系统以及试验对选取的最优解进行验证,仿真结果与试验结果验证了研究方法的正确性。
关键词:六关节机器人;逆向运动学;代数解析法;加权“最短行程”;最优解
0引言
六关节机器人结构紧凑、灵活性高、工作范围大,因而能很好地完成各种复杂任务并较早应用于工业领域。然而,六关节机器人的逆运动学求解具有一定的难度,在一定程度上制约着机器人工作效率的提高。目前机器人逆运动学求解的方法主要有代数解析法和数值迭代法:代数解析法运算速度快,实时性好,但机器人结构必须符合Pieper准则;数值迭代法可用于多数六关节机器人,但数值迭代法运算速度慢,且不能得到准确的逆解。工业六关节机器人结构比较规则,一般末端三个关节的轴线始终交于一点,符合Pieper准则,利用代数解析法求逆解具有优势。文献[5]比较了两种代数解析法的求解特点,却没有给出选取最优解的算法流程。文献[3]利用代数解析法求出8组逆解,利用“最短行程”准则选取了一组最优解。文献[1]在利用代数解析法求解时引用了复指数,虽然说明应根据实际情况选取最优解,却没有对如何选取最优解进行深入讨论。
本文在研究MOTOMAN-MH6机器人结构特点的基础上,利用D-H矩阵建立了机器人运动学模型,利用代数解析法得到了多重完整逆解,提出的加权“最短行程”准则能够根据MOTOMAN-MH6机器人的结构特点及实际需求选取最优解。
1MOTOMAN-MH6机器人运动学模型
图1为根据MOTOMAN-MH6机器人的结构特点,采用D-H方法建立的机器人各杆坐标系。
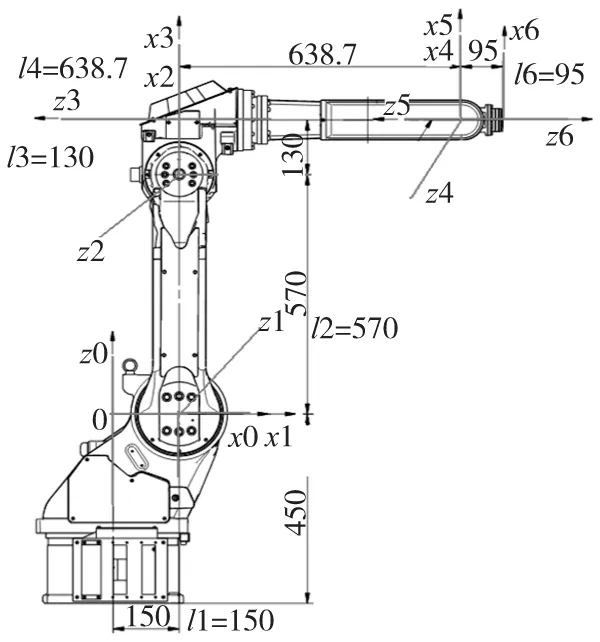
图1 MOTOMAN-MH6机器人结构及运动学坐标
坐标系{i-1}到坐标系{i}的变化矩阵为:

(1)
根据表1中MOTOMAN-MH6机器人运动学参数,其中θ值是各关节角处于初始状态的值,将各参数值代入式(1),可求出机器人末端姿态矩阵P和末端位置矩阵W。

表1 MOTOMAN-MH6机器人运动学参数
2代数解析法求逆运动学解
(1)求θ1。由L(3,4)=R(3,4)⟹
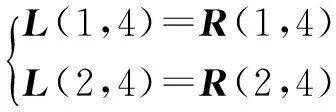
其中:
(3)求θ3。由第(2)步计算,可得:
θ3=Atan2(mL4+nL3,mL3-nL4)

其中:
h=sin(θ3-θ2)(αxcosθ1+αysinθ1)-αzcos(θ3-θ2)
(5)求θ4。由第(4)步计算,可得:
θ4=Atan2(f/sinθ5,g/sinθ5)
其中:
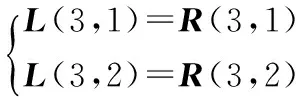

3多重逆解选取最优解
对于求出的多组逆解,首先判断其是否满足关节角的范围,剔除不满足条件的解或者将其转化为满足条件的解,将处理后的逆解代入式(1)进行验证,保证解的正确性和完整性。
目前机器人选取最优解一般采用“最短行程”准则,如图2所示。这种计算方法计算简单,却忽视了机器人各关节的差异性和实际需求,求出的最优解可能不是期望解。

图2 “最短行程”准则流程图
为了选出符合机器人结构特点的最优解,满足机器人实际工作需求,在基于“最短行程”准则的基础上,提出了一种加权“最短行程”准则,核心步骤就是通过求加权欧式距离最小值来选取最优解。加权“最短行程”准则如图3所示。

图3 加权“最短行程”准则流程图
给定权重函数的一种表达式为:
m为影响因子的个数,xk为第k个影响因子的值,pk为影响因子权重。
以MOTOMAN-MH6机器人为例,只考虑关节功耗和由关节转动引起后续连杆移动扫过的空间范围两个影响因子,此时m=2。转过相同角度各关节功耗之比为W1:W2:W3:W4:W5:W6,空间范围之比为S1:S2:S3:S4:S5:S6。此处,功耗之比经机器人测试可得出近似值,规定:
功耗影响因子的权重p1=0.3,杆移动空间范围影响因子权重p2=1-p1=0.7。此时,“最短行程”权重因子为:
将其带入加权“最短行程”准则公式中,可求出最优解。
在具体求解过程中,影响因子的个数和值应以机器人自身结构特点和运行状况为准,影响因子的权重根据实际需求给定。
4验证
MOTOMAN-MH6机器人逆运动学最优解的验证是通过实验室机器人三维仿真系统以及实体安川机器人来完成。将机器人末端三个连杆视为小连杆,其余为大连杆。当前机器人处于运动学初始状态,实验过程中期望机器人侧重移动小连杆以降低功耗、减少机器人连杆空间移动范围。依据实际需求计算出欧式距离的权重因子之比为:ω1:ω2:ω3:ω4:ω5:ω6=15:10:7:4:3:1。
如:输入6个关节角依次为:50,30,-50,50,100,-150。求出的末端位姿矩阵为:

按照“最短行程”准则选取的最优解为:-130.000000,38.961124,-47.832366,-52.608561,71.719043,40.621141。按照加权“最短行程”准则选取的最优解为:50.000000,30.000000,-50.000000,50.000000,100.000000,-150.000000。
表2为近似全局关节角试验数据,试验总组数为388962,按照“最短行程”准则和加权“最短行程”准则选出最优解不一致的组数为6392组,不一致组数占试验总组数的比例为1.64%。

表2 近似全局关节角试验数据
表3为局部关节角范围内的验证,试验总组数为15625,按照“最短行程”准则和加权“最短行程”准则选出最优解不一致的组数为11604组,不一致组数占试验总组数的比例为74.27%。
由加权“最短行程”准则公式可知:若六个关节角的欧式距离权重因子之比为1,加权“最短行程”准则将退化为“最短行程”准则,此时最优解不一致组数占试验总组数的比例为0%。因而,最优解不一致组数占试验总组数比例大小与末端位姿的范围以及欧式距离权重大小有关。
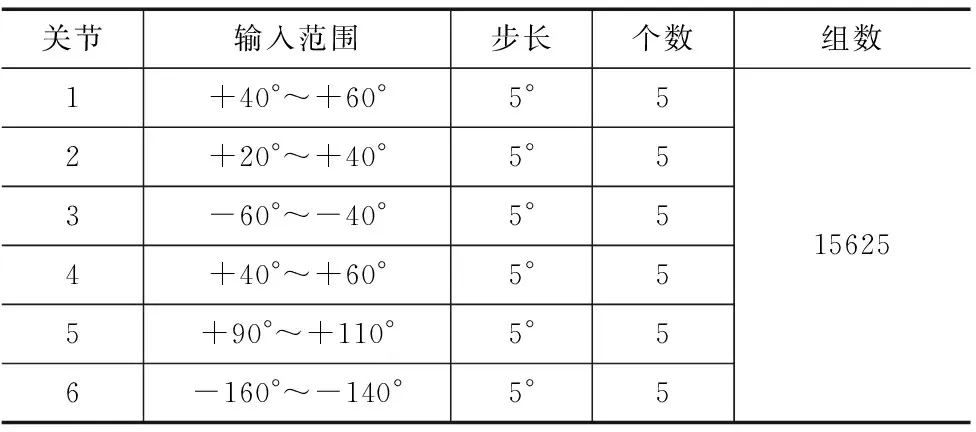
表3 局部关节角试验数据
假设“最短行程”准则选取的一组最优解为θ1,θ2,θ3,θ4,θ5,θ6;加权“最短行程”准则选取的一组最优解为θw1,θw2,θw3,θw4,θw5,θw6。令:
在局部关节角试验得到的11604组不一致最优解中均匀采取24组数据,具体分析如图4所示。
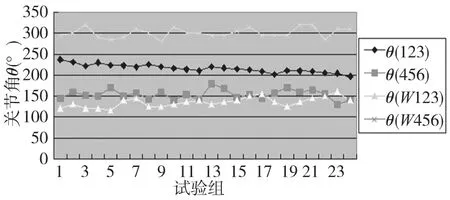
图4 加权优化前后效果对比图
由图4对比折线可以看出,加权“最短行程”准则在求逆解过程中侧重移动小连杆而不是大连杆,符合初始需求。
5结论
机器人逆运动学求解有一定的难度,利用代数解析法可以快速有效求出六关节工业机器人多重完整逆解;加权“最短行程”准则能够选取符合机器人结构特点和实际需求的逆解;机器人三维模型仿真系统和实体安川机器人对最优解进行验证,表明了研究方法的正确性,为进一步研究机器人轨迹规划奠定了基础。
[参考文献]
[1] 黎伯春,杨建宇,耿磊,等. 基于实时逆运动学算法的6R机器人三维仿真[J]. 组合机床与自动化加工技术,2014(3):45-48.
[2] John J Craig. 机器人学导论[M].北京:机械工业出版社,2012.
[3] 王其军,杜建军. MOTOMAN机器人逆运动学新分析[J].哈尔滨工业大学学报,2010,42(3):451-454.
[4] 张文明,云秀超,李晓旭,等. 六自由度弧焊机器人运动及位姿控制[J]. 制造业自动化, 2015,37(3):32-34.
[5] 程永伦. 钱江一号焊接机器人运动学研究及仿真分析[D]. 浙江:浙江大学,2008.
[6] 赵大旭,寿国忠,顾玉琦,等. 6自由度3P3R温室服务机械臂运动学分析[J]. 机床与液压, 2015,43(5):9-12.
[7] 林仕高. 搬运机器人笛卡尔空间轨迹规划研究[D]. 广州:华南理工大学,2013.
[8] Reza N Jazar. Theory of Applied Robotics: Kinematics, Dynamics, and Control[M]. 2rd.New York: Springer, 2010.
[9] 黎润伟. 面向复杂曲面加工的工业机器人离线编程系统研究[D]. 广州:华南理工大学, 2014.
[10] 王润. 串联机器人运动学分析、结构优化设计及仿真研究[D]. 天津:天津大学, 2012.
(编辑赵蓉)
Inverse Kinematics of Robot Based on Weighted Optimization
WANG Guang-dao1,2, LIU Yin-zhong2, SUN Wei-tang2
(1.Graduate University of Chinese Academy of Sciences, Beijing 100049, China; 2.Shenyang Institute of Computing Technology, Chinese Academy of Science, Shenyang 110168, China)
Abstract:Inverse kinematics is one of the key problems to realize the motion control of robot. How to determine the optimal solution quickly and accurately has been the hot spot at home and abroad. For this reason, the optimization of inverse kinematics for the MOTOMAN-MH6 robot is studied. The D-H Matrix is used to establish kinematics model, and the process of the algebraic analytic method is analyzed, and then the multiple complete inverse solutions are obtained. According to the structural features of robot and practical requirements, a weighted "shortest stroke" criterion is proposed, and the weight function is determined and a set of optimal solutions is selected. Finally, the optimal solution is verified by the robot 3D simulation system and the experiment, which proves the correctness of the research method.
Key words:six-joint robot; inverse kinematics; algebraic analysis; weighted "shortest stroke"; the optimal solution
文章编号:1001-2265(2016)05-0001-03
DOI:10.13462/j.cnki.mmtamt.2016.05.001
收稿日期:2015-06-14
*基金项目:“核高基”专项(2012ZX01029-001-002)
作者简介:王光道(1988—),男,河南漯河人,中国科学院大学硕士研究生,研究方向为数控技术,(E-mail)zezhen@126.com。
中图分类号:TH166;TP242.2
文献标识码:A
