基于遗传算法的多目标车间调度问题的研究*

张腾飞，马　跃,胡　毅，3，安　涛，王　帅，郭　安

(1.中国科学院大学，北京　100049； 2.中国科学院 沈阳计算技术研究所,沈阳　110004;3.沈阳高精数控智能技术股份有限公司,沈阳　110168)



基于遗传算法的多目标车间调度问题的研究*

张腾飞1,2，马跃2,胡毅2，3，安涛1,2，王帅1,2，郭安1,2

(1.中国科学院大学，北京100049； 2.中国科学院 沈阳计算技术研究所,沈阳110004;3.沈阳高精数控智能技术股份有限公司,沈阳110168)

摘要：文章讨论了一个多目标车间调度问题(JSP)。在JSP问题中我们考虑一个具有n个工件和m台机器的生产线，每道工序在不同的机器上完成且有各自的持续时间。JSP调度问题的目标是在所有工件的工序在m台机器上加工且不冲突的前提下找到一个最短的总调度时间。该文通过使用遗传算法来找到作业调度问题的最优方案。文中通过使用11种不同规格的标准测试用例来测试算法的性能。实验结果表明，实验的运行结果满足了调度要求，进一步证明了遗传算法的有效性和实用性。

关键词：作业调度；加工车间；遗传算法；启发式；多目标

0引言

在车间生产实际中，作业调度的好坏直接影响着企业的生产效率。车间作业调度问题[9](Job Shop Scheduling Problem，JSP)是组合优化问题中的一个典型的NP-hard问题，在过去的十多年中吸引了许多研究者的注意。文献[1]中作者研究了机器数目固定条件下的多目标车间调度问题，他们提出了一种两阶段的启发式方法来解决该问题。首先，基于优先级规则和禁忌搜索算法来得到一个可行解；然后，在此基础上用遗传算法来解决作业调度问题。文献[2]中作者研究了在有限的机器数目条件下求解车间调度问题的最短的总调度时间，他们提出了一种基于块邻域函数的高斯模糊启发式算法。遗传算法比较容易实现且可根据不同的调度问题相对容易地做出相应的调整，实验表明，它可以在可以接受的时间范围内求出理想的调度方案。有许多文献推荐使用遗传算法解决车间调度问题。文献[3]中作者实现了一种基于局部搜索算子的混合遗传算法。文献[4]中作者提出一种两阶段的算法实验方案，该算法分两阶段整合了基于规则的文化基因算法和转换瓶颈的再优化算法，实验结果表明该算法对车间调度问题正确且有效。

1车间作业调度问题描述

JSP问题是一个包含n个工件和m台机器的调度问题，其常用的数学描述如下：

Cmax≥ tij+ pijfor all (i,j)∈N

tkj≥tij+ pijforall(i,j)τ(k,j)∈A

tij≥tik+ pikforall(i,j)and(i,k)∈N

tik≥ tij+ pijforall(i,j)and(i,k)∈N

tij≥0forall(i,j)∈N

其中，Cmax表示完成所有工件加工后的最大完工时间，pij来表示工件j在机器i上的加工时间，tij表示工件j在机器i上的开始加工时间，N表示操作(i,j)的集合，A表示所有所有的工件j在机器k上加工前必须在机器i上加工操作依赖关系对(i,j)→(k,j)的集合。

2遗传算法简介

遗传算法是模拟、解决或优化问题的计算方法，它是受自然界中通过选择、交叉和变异来实现生物进化的启发而提出的。当遗传算法被应用到调度问题中，一个有效的调度序列被称作染色体或个体，每个个体都有自己的适应度值。遗传算法以迭代的方式运行，每次迭代代表了种群的一代。每一代种群个体包括上一代的幸存者和新的经过交叉、变异和选择后而新产生的比较优秀的个体。不同的染色体是否被选择是由它们的适应度值来决定的，适应度越值大，被选中的概率越大。在实验中这种选择机制一直被重复，直至满足给定的条件为止。

3遗传算法解决车间调度问题

本文中将分以下几个步骤来介绍遗传算法。

3.1问题建模

本文将用两个二维数组machineNoMatrix[][]和timeMatrix[][]来分别表示第i个工件的第j道工序所使用机器的机器号和所耗费的时间，数组的行号和列号分别代表了工件的工件号和工序号，当第i个工件的第j道工序不存在的话，令machineNoMatrix[i-1][j-1]=-1，timeMatrix[i-1][j-1]=0。

3.2编码

染色体序列的长度为n×m，n表示工件的数量，m表示机器的数量，染色体序列的每一个元素是[1,n]之间的一个随机数，该数字在序列中第几次出现表示它所代表工件的第几道工序，本文采用的是基于间接工序的编码方法[12]。例如，对于一个3个工件×4台机器的作业调度问题,其染色体的大小为12(3×4)。工件1可以用数字1来表示，它重复出现3次表示工件1有3道加工工序。

3.3解码

我们从左到右解码一个染色体序列，下面以一个3个工件×4台机器的车间调度问题为例来说明解码规则：

图1一个3×4车间调度问题的染色体实例

如图1所示，染色体序列的第一个元素为1，表示工件1，而工件1第一次出现表示是工件1的第一道工序。然后再以第六个元素1例，它表示工件1的第三道工序。我们可以从如图1所示的染色体编码序列中获得当前执行到哪个工件的哪一道工序。

3.4初始化种群

首先随机产生一个300条染色体大小的种群，每条染色体代表一个个体，即一个可行的作业调度序列。

3.5适应度值计算

本文的适应度值的取值为各个工件完成所有加工操作的最大完工时间(Cmax)。根据帕累托最优原则，每个染色体的适应度值代表该染色体的优势排名。

求解车间调度的最短的总调度时间的难点在于：一方面，各个工件不同的工序之间有严格的先后顺序；另一方面，同一台机器在某个时刻只可以加工一种工件。各个工件不同的工序之间有严格的先后顺序这个问题已经在染色体编码序列中已经被解决，因为染色体序列中各个工件出现的顺序就代表着各个工件的工序序列。而同一台机器某个时刻只可以加工一种工件这个问题可以通过维护一个机器数目大小的一维数组来实现，数组存储的值是该机器处理完当前工件后的空闲时间点。

车间调度执行的顺序是按染色体编码序列的顺序从左向右执行，由调度问题的执行位置和染色体编码序列可知要加工工件的工件号i，然后通过工件号在染色体序列的当前位置获得该工件所在的工序号j，由工件号和工序号从二维数组machineNoMatrix[][]和timeMatrix[][]获得第i个工件的第j道工序所使用的机器号和所耗费的时间，然后更新第i个工件第j道工序的开始时间为第i个工件第(j-1)道工序的结束时间或该工序将要使用机器的最近空闲时间点的之中的较大者，更新第i个工件第j道工序的结束时间为该工序的开始时间与加工时间之和，更新该工序所使用机器的最近空闲时间点为第i个工件第j道工序的加工完成时间。如果该工序的完工时间大于当前的最大完工时间，更新最大完工时间的值，直至染色体序列中的所有工序至所有工序被加工完毕，最终可以获得完成车间调度所需的最大完工时间，即适应度的值。

3.6选择

在每一个连续的父代子代中，父代的一部分被选择来产生新的一代，然后基于适应度值来选择新产生的个体，适应度越大的个体越有可能被选中，本文将轮盘赌策略和精英策略相结合的方式来选择交叉和变异步骤所需的候选染色体。

3.7交叉和变异

本文测试了三种交叉算子(顺序交叉：OX[5],循环顺序交叉：COX[6],混合顺序交叉：MOX[7])和两种变异算子(逆转变异：OBM[8]和互换的基因突变：SBM[8])，在完成这六种可能的交叉、变异对的测试后，本文保留了顺序交叉(概率P=0.95)和逆转变异(P=0.02)操作符。下面就分别简要介绍下本文所用到的交叉和变异算子。

3.7.1逆转变异算子

染色体中的两个值交换它们的位置，如图2所示。

图2　逆转变异算子示例

3.7.2顺序交叉算子

对于一个n个工件×m台机器的车间调度问题，首先产生范围在[1,n×m]的两个随机数且第一个随机数小于第二个随机数，n×m是染色体编码序列的长度，产生的两个随机树代表父代染色体的要遗传给子代染色体的染色体序列的起始和结束位置，在本例中的两个随机数分别为3和5。父代染色体的部分编码序列被子代继承：Father 1的编码序列(3 1 1)被Child 1继承，Father 2的编码序列(3 2 1)被Child 2继承。

Child 1:[_,_,_,3,1,1,_,_,_]，继承的工序分别为工件3的第二个工序和工件1的第一个和第二个工序。

Child 2:[_,_,_,3,1,1,_,_,_]，即：继承的工序分别为工件3第一个工序，工件2第二个工序和工件1第三个工序。

为了获得Child 1染色体的其它工序项：

(1)先我们以Father 2为模板从第二个随机数5所在的位置后面开始循环构造一个新的染色体序列：(2 3 3///2 1 1 3 2 1)。

(2)我们将已经从Father 1中继承的工件序列从新产生的染色体序列中移除(即：工件3的第二个工序和工件1的第一个和第二个工序)：由(2 3 X 2 X X 3 2 1)获得(2 3 2 3 2 1)。

(3)填充Child 1剩余部分 ：首先从第二个随机数所代表的位置后面开始填充得到[_, _ , _ , 3, 1, 1, 2, 3 , 2]，然后循环填充得到最终序列[3, 2, 1, 3, 1, 1, 2, 3, 2]。

同理可求得Child 2的其它工序项。顺序交叉算子的具体用法如图3所示。

图3　顺序交叉算子示例

3.8停止条件

遗传算法运行到最短的总调度时间达到给定下限或者迭代次数达到2000次。

4实验结果

本文的计算实验用MyEclipse 10完成，所用CPU为2.6GHz的Core i5处理器，内存大小为4G。为了评估遗传算法的性能，笔者使用了Muth & Thomson和Lawrence设计共11种不同规格标准测试用例来进行计算实验，工件的数目为6到30不等，机器的数目为5到15不等。如表1所示，本文比较了遗传算法、模拟退火算法和禁忌搜索算法的性能。本文所使用的遗传算法的参数为：交叉率：0.95，变异率：0.02，群体规模为200，迭代次数为2000。

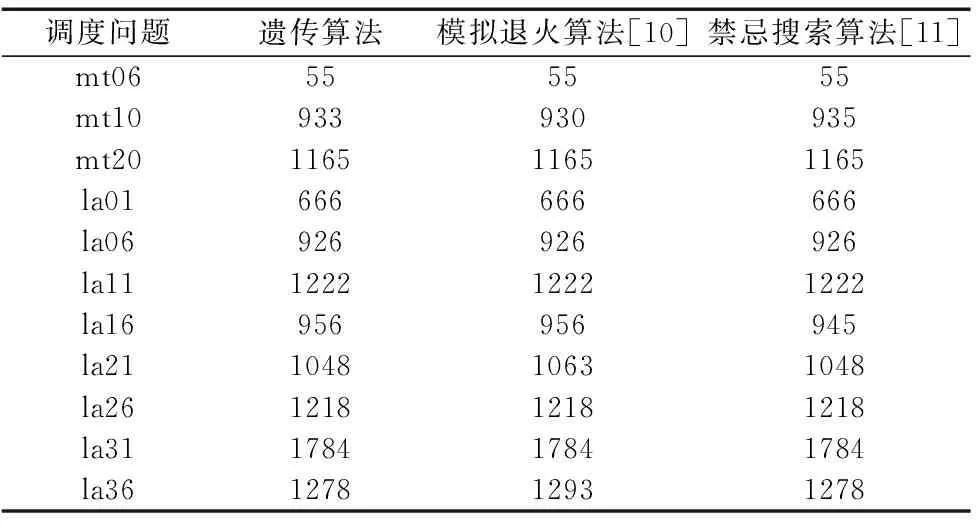
表1　遗传算法与文献[10-11]中的比较结果

通过对比，由表1中的数据不难得出结论：本文的遗传算法和文献[10-11]中的算法性能相当，几乎每个标准测试用例都能达到或接近于最优解。考虑到图片中文字的可读性，本文以小规模的作业调度问题mt06为例将其最佳调度以甘特图的形式展示出来。本文的甘特图是在mt06调度数据的基础上绘制的，其具体调度信息如图4所示。图中p(i,j)表示工件j在机器i上的加工时间，i表示机器i，j表示工件j。以机器M6上加工的第一个工件为例，比较各个机器的加工序列后可知，它属于工件3的第三道工序，p(6,3)=8表示在机器号为6的机器上加工的工件3所需的时间为8。

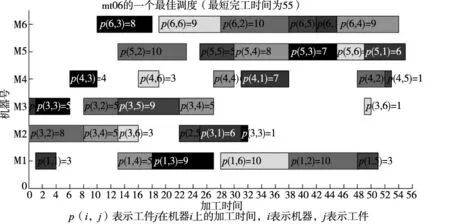
图4　mt06的一个最佳调度(最短的总调度时间为55)

5结论和后期工作

本文针对流程工业中的JSP问题，建立了相应的数学模型，在调度模型的基础上应用遗传算法，针对标准的测试用例求解车间调度问题的最优调度方案。大量的计算实验表明，在解决车间调度问题时本文所采用的遗传算法所求得的解和文献[10-11]中的最优结果相比性能优异，具有较高的求解质量和效率。尽管如此，由于遗传算法也有其固有的缺点，比如过早收敛和计算量大等，今后在这些方面仍需改进。下一步，我将通过以下三个方面来研究车间调度问题：

(1)用一种混合的选择标准来选择给定染色体群体中的最好个体。

(2)选择关键路径上的关键机器加工的工序来对染色体序列进行交叉。

(3)采用混合算法来解决遗传算法过早收敛和计算量大的缺陷。

[参考文献]

[1] N Zribi, A Kamel, P Borne. Minimizing the makespan for the MPM job-shop with availability constraints[J].International Journal of Production Economics, 2008, 112(1):151-160.

[2] Y Mati. Minimizing the makespan in the non-preemptive job-shop scheduling with limited machine availability[J]. Computers & Industrial Engineering, 2010, 59: 537-543.

[3] R Qing-dao-er-ji,Y Wang. A new Hybrid genetic algorithm for job shop scheduling problem[J]. Computer & Operations Research, 2012, 39: 2291-2299.

[4] H C Cheng, T C Chiang, L C Fu. A two-stage hybrid memetic algorithm for multi-objective job shop scheduling[J]. Expert Systems with Applications, 2011, 38: 10983-10998.

[5] Davis L. Adapting operator probabilities in genetic algorithms[C]. Proceedings of the third international conference on Genetic Algorithms, 1989:375-378.

[6] G W Woods. A hybrid genetic algorithm that adapts to binary and real coded operators[J]. 1997.

[7] M Ben Ali, M Sassi, M Gossa, et al.Simultaneous scheduling of production and maintenance tasks in the job shop[J]. International Journal of Production Research, 2011, 49(13): 3891-3918.

[8] Mattfeld D C. Evolutionary search and the job shop[J]. Investigations on genetic algorithms for production scheduling, 1995.

[9] 安晶,秦珂. 一种基于遗传算法的车间调度算法求解[J]. 盐城工学院学报,2007,20(1):33-36.

[11]Dell A M,Trubian M. Applying Tabu Search to the Job Shop Scheduling Problems[J]. Annual Operations Research, 1993, 40:231-252.

[12] 姜迪刚,叶尚辉. 基于遗传算法的车间作业调度[J]. 西安电子科技大学学报,2001,28(2):207-210.

(编辑赵蓉)

Multiobjective Genetic Algorithm-Based Method for Job Shop Scheduling Problem

ZHANG Teng-fei1,2, MA Yue2,HU Yi2,3, AN Tao1,2, WANG Shuai1,2,GUO An1,2

(1. Chinese Academy of Sciences, Beijing 100049, China;2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110004, China)

Abstract：In this paper we consider a multiobjective job shop scheduling problem (JSP). In JSP we consider m machines on a production line with n defined jobs, each job consists of different tasks for different machines and each of them has its own duration. The goal is to find the shortest scheduling in which none of the jobs' tasks collide on all of the m machines. This part uses the Genetic Algorithm to find the optimal solution for the job scheduling problem. Performance of the proposed heuristic is evaluated through computational experiments on 11 different sizes benchmarks. The result of the test shows the efficiency of search is increased and the convergence is improved in shop scheduling with the Genetic Algorithm.

Key words：scheduling; job shop; genetic algorithms; heuristic; multiobjective

文章编号：1001-2265(2016)05-0043-03

DOI:10.13462/j.cnki.mmtamt.2016.05.012

收稿日期：2015-06-09

*基金项目：“高档数控机床与基础制造装备”国家科技重大专项:基于二次开发平台的专用数控系统开发与应用(2013ZX04007-011)

作者简介：张腾飞(1989—)，男，河南商丘人，中国科学院大学、中科院沈阳计算技术研究所硕士研究生，研究方向为实时系统与数控技术，(E-mail)mnmlist@163.com；马跃(1960—)，男，中科院沈阳计算技术研究所博士生导师，研究员，研究方向为数据挖掘、信息系统。

中图分类号：TH165；TG506

文献标识码：A