Symmetries and Their Lie Algebra of a Variable Coefficient Korteweg-de Vries Hierarchy∗

Xiaoying ZHU Dajun ZHANG

1 Introduction

Nonlinear evolution equations with variable coefficients play important roles in applications,as in inhomogeneous plasmas,optical fibers,viscous fluids and Bose-Einstein condensates.Usually,these equations are not integrable,or are only nearly integrable.Although there is no exact definition for what the integrability is,there are many approaches to getting clues,such as integrable characteristics,which link a nonlinear system to being integrable.These integrable characteristics,including passing the Painlev´e test,having a Lax pair,having multi-Hamiltonian structures,in finitely many symmetries,in finitely many conserved quantities,having bilinear forms,multi-soliton solutions,and so on,are deeply linked to each other.Let us take the following vcKdV equation:

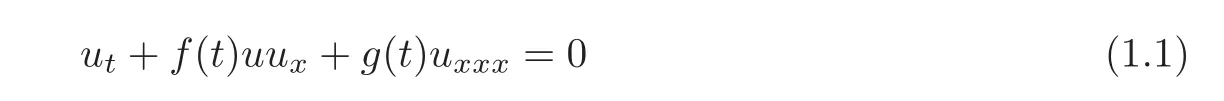
as an example.This equation was first proposed by Grimshaw[1]in 1979 and has been widely studied.As far as the integrability is concerned,the vcKdV(1.1)can pass the Painlev´e test under the condition,given by Joshi[2]in 1987,

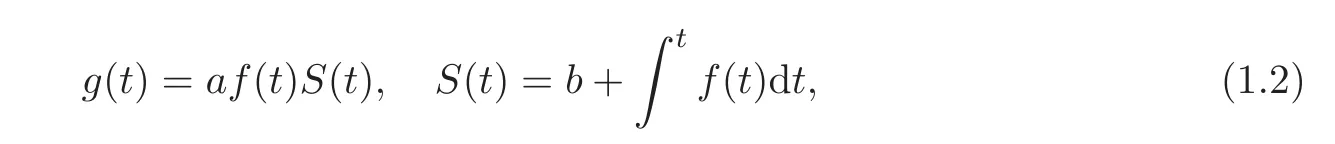
where a and b are real constants and a0.This is also the condition when the vcKdV equation(1.1)has a Lax pair,a bilinear form,N-soliton like solutions and in finitely many conservation laws(see[3–5]).There are also many results(see[6–7])on the integrability of(1.1)with special forms of f(t)and g(t)which agree with(1.2).

In this paper,we would like to construct the in finitely many symmetries of the vcKdV(1.1)under the condition(1.2).We will first start from the Lax pair of(1.1)to derive isospectral and non-isospectral hierarchies and the related formal recursion operator(which is not a rigorous recursion operator and contains t explicitly).Then we discuss the hereditary and strong symmetry properties of the formal recursion operator.By these properties we can construct a Lie algebraic structure of adjoint flows,and finally we get,for the isospectral vcKdV hierarchy,two sets of symmetries,which also form a Lie algebra.

The paper is organized as follows.In Section 2,we introduce some basic notions.In Section 3,we derive isospectral and non-isospectral vcKdV hierarchies.Finally,we investigate the symmetries and their Lie algebra for the isospectral vcKdV hierarchy.

2 Basic Notions

Let us first recall some basic notions and properties related to symmetries.

Suppose that V is a function space consisting of scalar functions f(t,x)which are C∞differentiable with respect to t and x,the functions u=:u(t,x),K(u)=:K(t,x,u,ux,uxx,···)∈ V,and Φ =:Φ(t,x,u)is an operator living on V.For the functions f(u),g(u)∈ V and the operator Φ,the Gateaux derivatives of f and Φ in the direction h w.r.t.u are defined as

Forwe define the product(a commutator)

By the commutator we define the symmetry,τ=:τ(t,x,u),of the nonlinear evolution equation

if

where bywe specially denote the derivative of τ with respect to t explicitly included in τ.If τ1and τ2are symmetries of(2.2),then[[τ1,τ2]]is also a symmetry for(2.2).

The operator Φ is called a strong symmetry(see[8])of the evolution equation(2.2),if

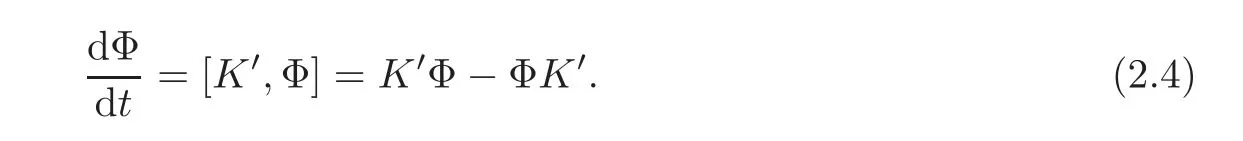
That Φ is a strong symmetry of(2.2)means that if τ is a symmetry of(2.2),so is Φτ.If Φ satisfies

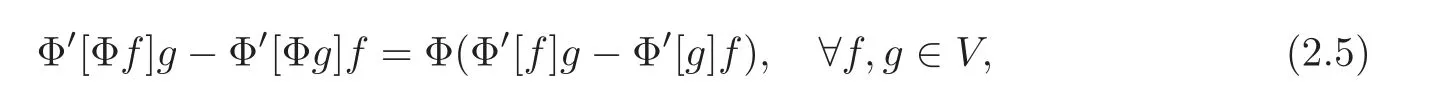
then Φ is called a hereditary operator(see[8–9]).For a operator Φ which satisfies Φ0=0 and does not explicitly contain tif Φ is hereditary and is a strong symmetry of(2.2),then it is a strong symmetry for all the equations(see[8])

Such Φ is referred to as a strong hereditary symmetry(see[8])for the hierarchy(2.6).For convenience of later use,we redescribe the property by the following proposition.

Theorem 2.1IfΦis a hereditary operator satisfyingΦ0=0and also

then

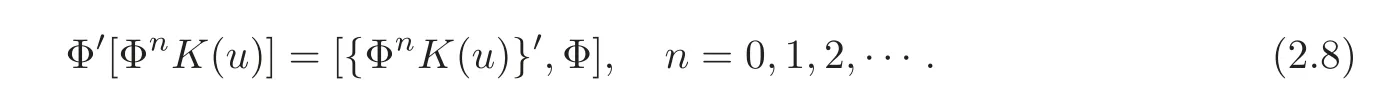
3 Isospectral and Non-isospectral vcKdV Hierarchies

In this section,we derive the isospectral and non-isospectral vcKdV hierarchies.We start from the spectral problem(see[5])

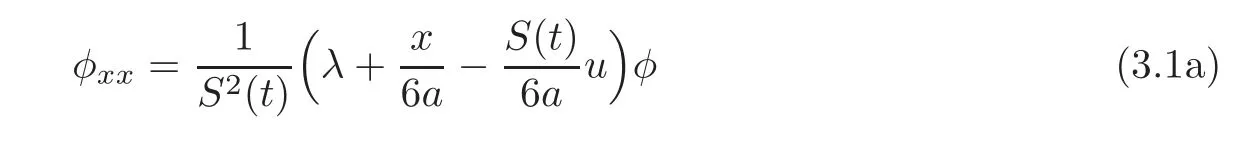
with the time evolution

The compatibility condition φxxt= φtxxyields

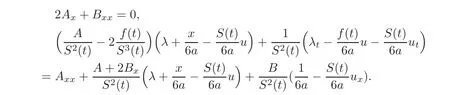
Further,we have

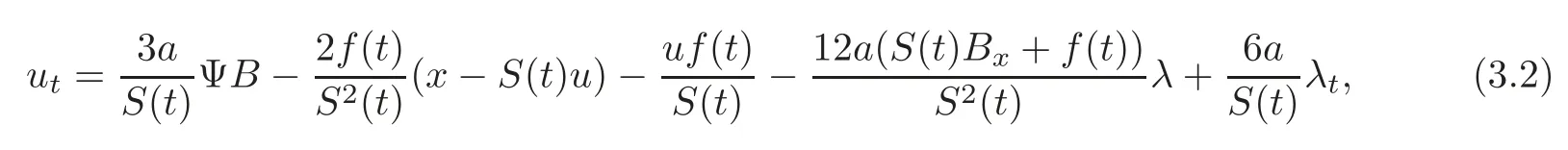
where Ψ is an operator defined by

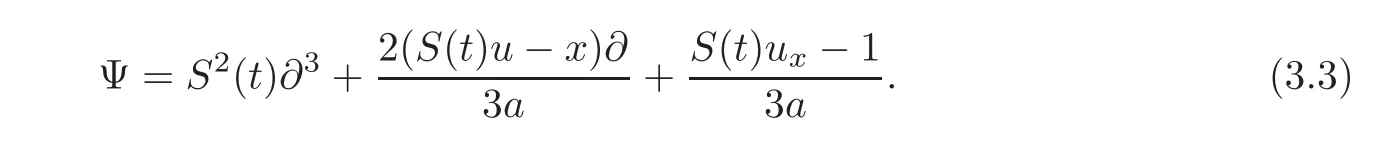
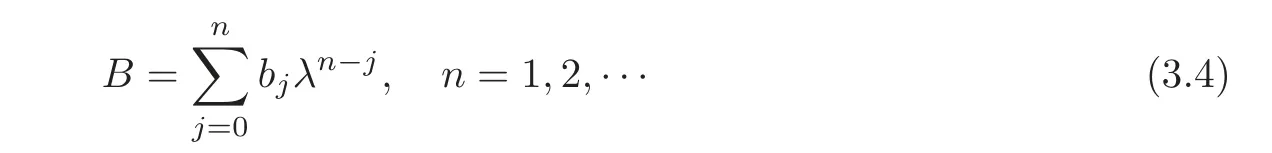
Substituting the expansion into(3.2)and comparing the coefficients of the same powers of λ yield

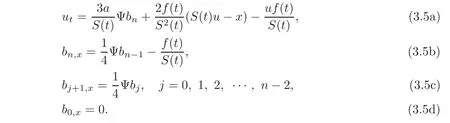
Taking λt=0 and

we have

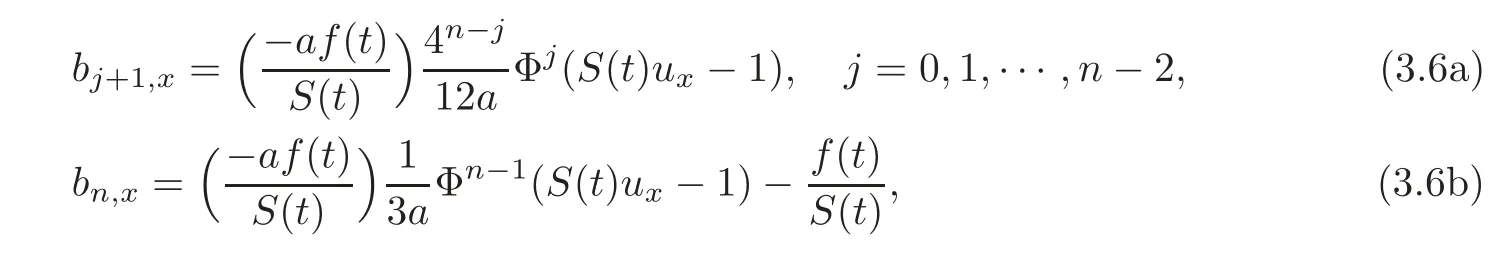
where

Then we get the isospectral vcKdV hierarchy

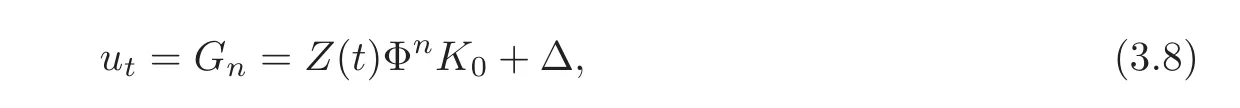
where

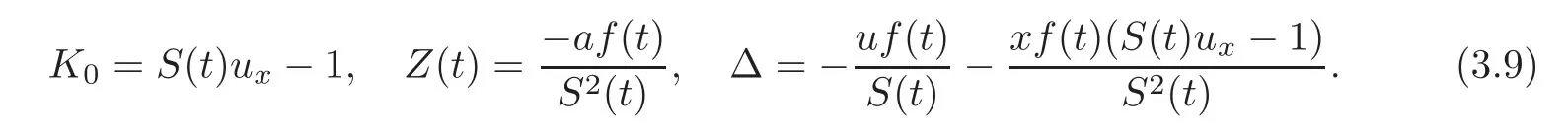
This hierarchy can be formally extended to starting from n=0.When n=1,it just gives the vcKdV equation(1.1).Besides,the Lax pair of vcKdV(1.1)is provided by(3.1)with

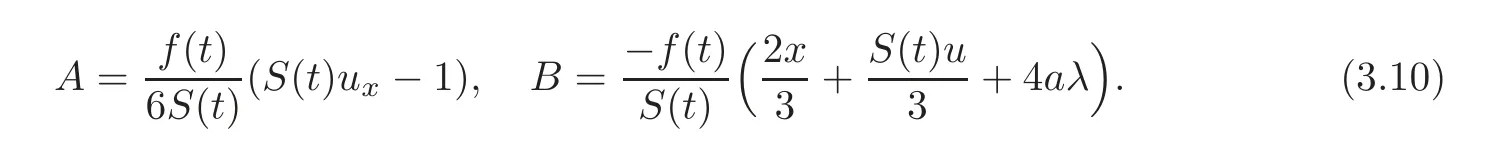
In the non-isospectral case,we suppose that

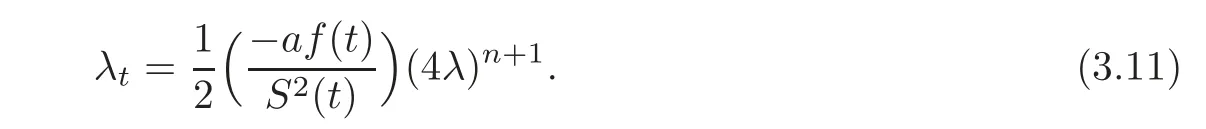
In this case,still using the expansion(3.4)but takingsimilar to the isospectral case,we can have the following non-isospectral vcKdV hierarchy:

where

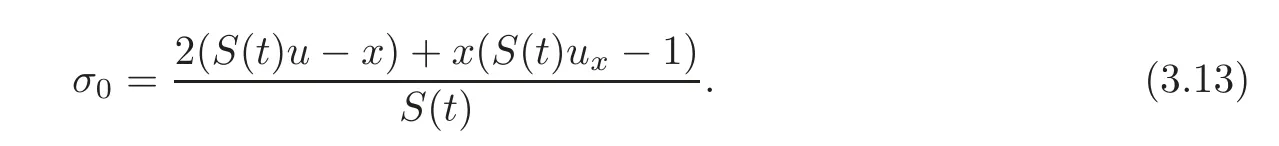
Now we have obtained the isospectral vcKdV hierarchy(3.8)and the non-isospectral hierarchy(3.12).Besides,as by-products,we get two sets of flows,

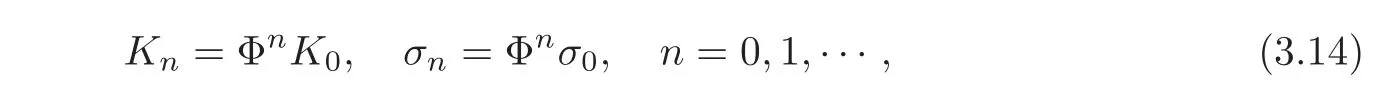
which we call adjoint flows in this paper.The recursion operator Φ for the adjoint flows is not a rigorous recursion operator,but a formal one for the vcKdV hierarchies.

4 Symmetries and Their Lie Algebraic Structures

In this section,we will derive two sets of symmetries for the isospectral vcKdV hierarchy(3.8),and we will also prove that these two sets of symmetries form a Lie algebra.

Our tactic goes as follows.First,we prove that the formal recursion operator(3.7)is a hereditary operator and is further a strong symmetry for the isospectral vcKdV hierarchy(3.8).Next we show that the adjoint flows{Kn}and{σn}form a Lie algebra with respect to the commutator(2.1).Then we prove that the arbitrary member ut=Glin the hierarchy(3.8)has two ground symmetries K0and,and also we can get two sets of symmetries by acting Φ.Finally we show that the obtained symmetries form a Lie algebra.In fact,there are many ways for deriving two sets of symmetries(usually called K-symmetries and τ-symmetries)starting from a Lax pair(see[10–17]).Our tactic copies these ideas more or less,while the procedure contains some generalization and specialization since Φ contains t explicitly and is not a rigorous recursion operator.

4.1 The strong hereditary symmetry Φ

Let us start from the following lemmas related to the operator Φ given by(3.7).

Lemma 4.1Φis a strong symmetry of the first equation in(3.8),that is,

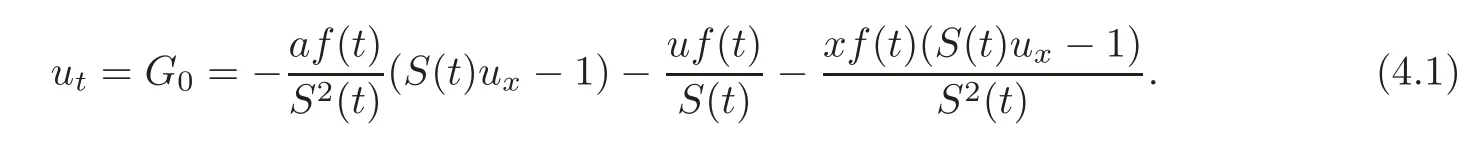
In fact,by a direct calculation we can find that Φ and G0satisfy

where we should make use of the fact=f(t)and the expression of utgiven by(4.1).

By the similar direct veri fication(but here we skip the tedious process),we find the following results.

Lemma 4.2Φis a hereditary operator satisfying(2.5).

Lemma 4.3Φsatisfies

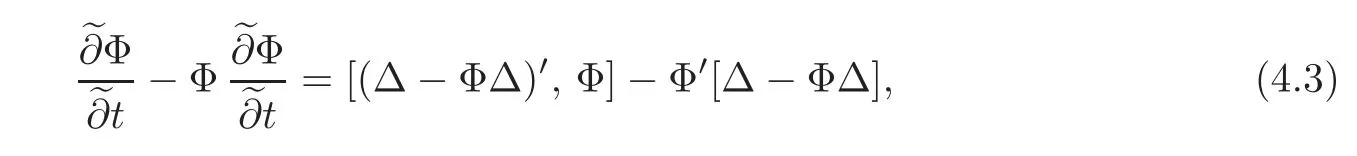
whereΔis given in(3.9).

With these lemmas in hand,we can reach the final results of this subsection.

Theorem 4.1The operatorΦgiven by(3.7)is a strong hereditary symmetry for the isospectral vcKdV hierarchy(3.8).

现阶段建筑施工当中仍然存在管理不规范的现象。比如：施工人员没有依照相应的用电与节电标准进行，并且在施工现场相应的安全警示标志较少，使施工现场的整体状况仍处于不规范的情形当中。除此以外还有很多建筑企业在制定施工方案以及制度的时候仍存在很多不规范的地方，特别是施工方技术交底情况，并且在这样的不规范情况下作业人员也无法记录真实的施工活动，最终使得施工安全管理工作受到影响。

ProofWe prove the theorem by the reductive method.By virtue of Lemma 4.1,we suppose that Φ is a strong symmetry of the equation ut=Gnsatisfying

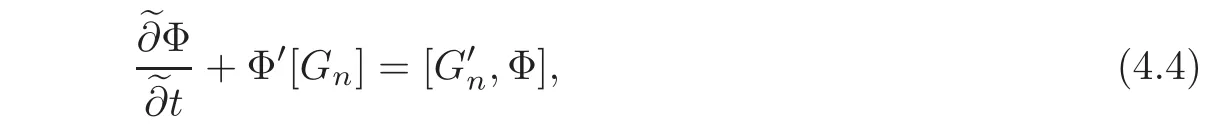
and we next go to prove

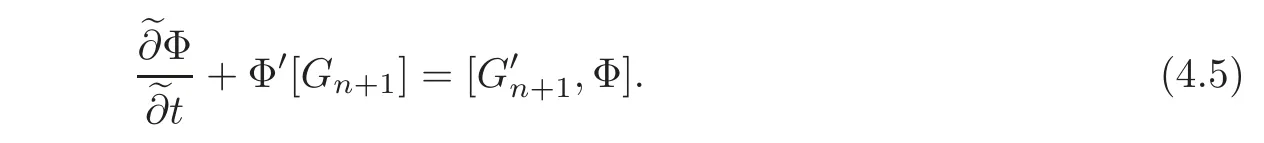
Since

(4.5)becomes

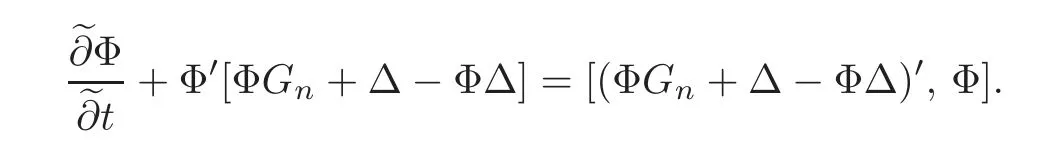
Further,

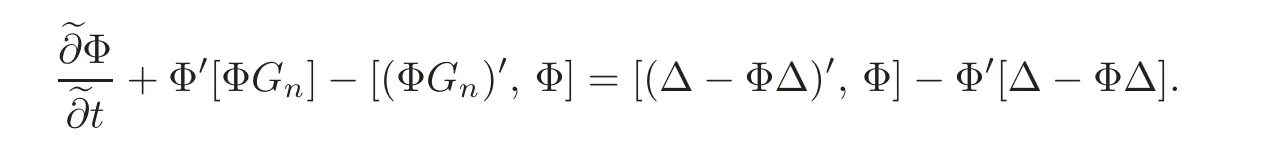
So by virtue of(4.3),we only need to prove

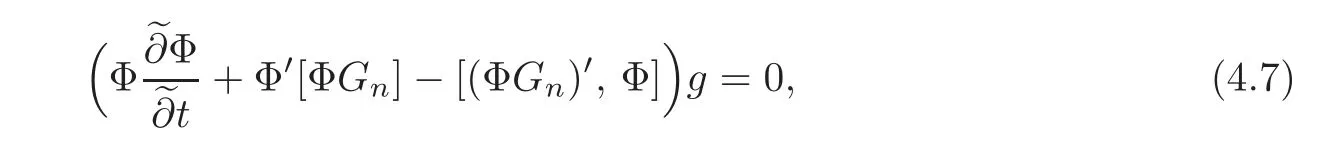
where g is an arbitrary function.Using(4.4)to replaceand then making use of the formula

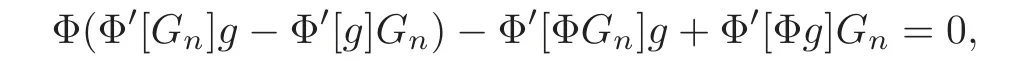
which is true due to the hereditariness of Φ.We note that in(4.8),Φ ◦a'[b]specially means that Φ applies to the function a'[b].The proof is completed.

4.2 Lie algebra of the adjoint flows

In this subsection,we discuss the algebra relationship of the adjoint flows{Kn}and{σm}which were given in(3.14).

Let us start from the relations of Φ and the flows{Kn}and{σm}.

Lemma 4.4For the adjoint flows{Kn}and{σm},we have

and

ProofWe only prove(4.10).From

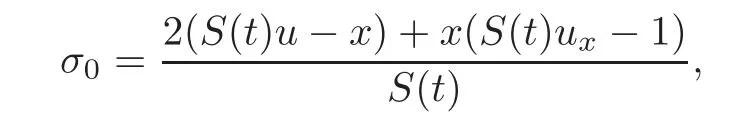
it is easy to see that

Then(4.10)holds for n=0.Now we suppose that(4.10)holds for n=k,as in the following form

Then,by the formula(4.8),for arbitrary ν∈V,we have

Thus we have completed the proof.

Now we can check some relations between simple adjoint flows.By calculations we find

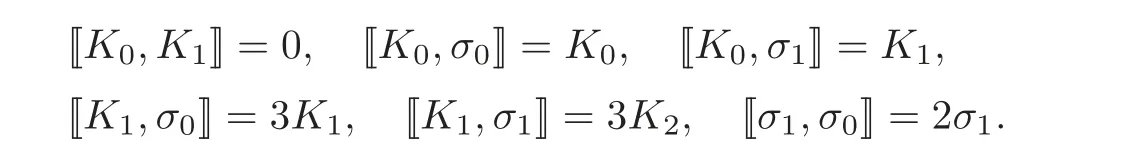
Starting with these relations and using Lemma 4.4,by the reductive method,we can prove the following general relations.

Theorem 4.2The adjoint flows{Kn}and{σn}form a Lie algebra with respect to the commutator(2.1)of the following structure:

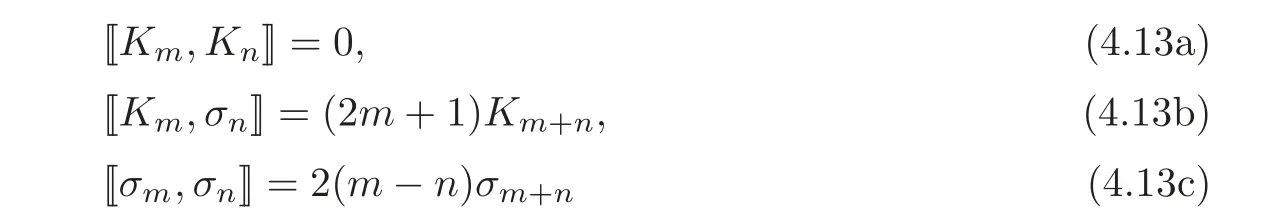
form,n=0,1,2,···.

4.3 Symmetries and Lie algebra

Now we consider symmetries for the arbitrary isospectral equation First,it is easy to check that

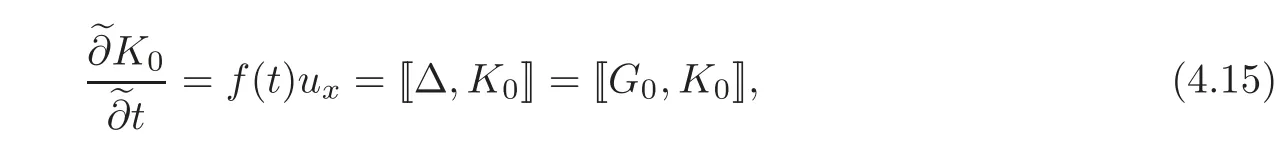
which means that K0is a symmetry of the equation ut=G0.Further,by virtue of(4.13a),we have

This means that K0is a symmetry for the equation(4.14).Since we have shown that Φ is a strong symmetry of(4.14)in Theorem 4.1,all the flows

are symmetries of(4.14).This further leads to

and from(4.13a),

Next we derive another set of symmetries of(4.14).

Lemma 4.5

are symmetries of(4.14)forl=0,1,2,···.

ProofSince Φ is a strong symmetry of(4.14),we only need to prove

is a symmetry of(4.14).Noting that

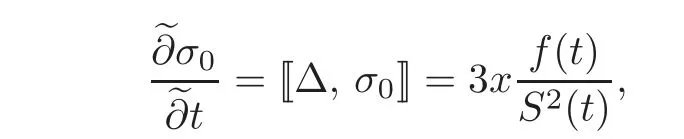
together with(4.19)and(4.13b),it is easy to get

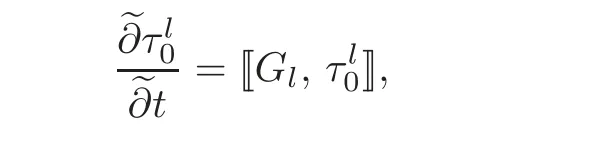
which means thatis a symmetry of ut=Gl.

As a by-product,we have

Thus we already have two sets of symmetries for the equation(4.14),i.e.,{Kn}and{},which are usually referred to as K-symmetries and τ-symmetries,respectively.These symmetries can form a Lie algebra by the algebra relation(4.13).We conclude these by the following theorem.

Theorem 4.3The equation(4.14)ut=GlhasK-symmetries{Kn}andτ-symmetries{},which form a Lie algebra with the structure

form,n=0,1,2, ···.

5 Conclusion

Under the Painlev´e-integrable condition(1.2),we have derived isospectral and non-isospectral vcKdV hierarchies.We proved that the formal recursion operator Φ is a strong hereditary symmetry of the isospectral hierarchy,although it contains t explicitly and is not a rigorous recursion operator.By the relation between Φ and the adjoint flows{Kn}and{σm},we proved that{Kn}and{σm}form a Lie algebra.Then,by constructing ground symmetries,we got two sets of symmetries for the isospectral vcKdV hierarchy.Finally,the two sets of symmetries are shown to form a Lie algebra.During the above procedure,the adjoint flows{σm}play the role of master symmetries(see[18]).

[1]Grimshaw,R.,Slowly varying solitary waves,I.Korteweg-de Vries equation,Proc.Royal Soc.Lon.A-Math.Phys.Engin.Sci.,368,1979,359–375.

[2]Joshi,N.,Painlev´e property of general variable-coefficient versions of the Korteweg-de Vries and nonlinear Schrödinger equations,Phys.Lett.A,125,1987,456–460.

[3]Zhang,Y.C.,Yao,Z.Z.,Zhu,H.W.,et al.,Exact analytic N-soliton-like solution in Wronskian form for a generalized variable-coefficient Korteweg-de Vries model from plasmas and fluid dynamics,Chin.Phys.Lett.,24,2007,1173–1176.

[4]Zhang,Y.C.,Li,J.,Meng,X.H.,et al.,Existence of formal conservation laws of a variable-coefficient Korteweg-de Vries equation from fluid dynamics and plasma physics via symbolic computation,Chin.Phys.Lett.,25,2008,878–880.

[5]Zhang,D.J.,Conservation laws and Lax pair of the variable coefficient KdV equation,Chin.Phys.Lett.,24,2007,3021–3023.

[6]Hong,W.and Jung,Y.D.,Auto-Bäcklund transformation and analytic solutions for general variablecoefficient KdV equation,Phys.Lett.A,257,1999,149–152.

[7]Fan,E.G.,Auto-Bäcklund transformation and similarity reductions for general variable coefficient KdV equations,Phys.Lett.A,294,2002,26–30.

[8]Fuchssteiner,B.and Fokas,A.,Symplectic structures,their Bäcklund transformations and hereditary symmetries,Physica D,4,1981,47–66.

[9]Fuchssteiner,B.,Application of hereditary symmetries to nonlinear evolution equations,Nonlinear Analysis,TMA,3,1979,849–862.

[10]Ma,W.X.,K-symmetries and τ-symmetries of evolution equations and their Lie algebras,J.Phys.A:Math.Gen.,23,1990,2707–2716.

[11]Ma,W.X.,The algebraic structures of isospectral Lax operators and applications to integrable equations,J.Phys.A:Math.Gen.,25,1992,5329–5343.

[12]Ma,W.X.,Lax representations and Lax operator algebras of isospectral and nonisospectral hierarchies of evolution equations,J.Math.Phys.,33,1992,2464–2476.

[13]Ma,W.X.and Fuchssteiner,B.,Algebraic structure of discrete zero curvature equations and master symmetries of discrete evolution equations,J.Math.Phys.,40,1999,2400–2418.

[14]Tamizhmani,K.and Ma,W.X.,Master symmetries from Lax operators for certain lattice soliton hierarchies,J.Phys.Soc.Jpn.,69,2000,351–361.

[15]Chen,D.Y.and Zhang,H.W.,Lie algebraic structure for the AKNS system,J.Phys.A:Gen.Math.Phys.,24,1991,377–383.

[16]Chen,D.Y.and Zhang,D.J.,Lie algebraic structures of(1+1)-dimensional Lax integrable systems,J.Math.Phys.,37,1996,5524–5538.

[17]Tian,C.,Symmetries,in Soliton Theory and Its Applications,Gu C.H.ed.,Springer-Verlag,Berlin,1996.

[18]Fuchssteiner,B.,Master symmetries,higher order time-dependent symmetries and conserved densities of nonlinear evolution equations,Prog.Theo.Phys.,70,1983,1508–1522.