On the GF(p)Linear Complexity of Hall’s Sextic Sequences and Some Cyclotomic-Set-Based Sequences∗

Xianmang HELiqin HUDong LI

1 Introduction

The linear complexity of a periodic sequence is an important standard to scale the randomicity of key streams,and plays an important role in the application of the sequence in cryptography and communication.The linear complexity of a periodic binary sequence is defined as the length of the shortest linear feedback shift register to generate the sequence.The periodic binary sequences with a low linear complexity(L)are not secure,since the Berlekamp-Massey algorithm(see[1])can be used to construct the whole sequences with only 2L consecutive elements of the sequence.

Klapper[2]demonstrated that there exists a class of binary geometric sequences of the period qn−1(q is a prime power pmand p is an odd prime)with the maximal possible linear complexity qn−1 when considered as sequences over GF(2),but these sequences have very low linear complexities when applied as sequences over GF(p).This pioneering work suggests that the binary sequences with high GF(2)linear complexities are not necessarily cryptographically secure,since they can not prevent the attacker to get the whole sequence over GF(p)whose GF(p)linear complexity is low.Thus,much effort has been paid to find out ways of determining the GF(p)linear complexities.Chen and Xu[3–4]proposed some constructions of the binary sequences with high GF(2)linear complexities but low GF(p)linear complexities,and gave some lower bounds of the GF(p)linear complexities of Blum-Blum-Shub,self-shrinking,and de Bruijn sequences,etc.He has done a study of the GF(p)linear complexity of Legendre sequences(see[5]).

For the cryptographic purpose,we should study the linear complexity of the binary sequence considered as a sequence over GF(p),whose elements happen to be 0 or 1.Motivated by this perspective,we study the problem of the GF(p)linear complexity of Hall’s sextic sequences and some cyclotomic-difference-set-based sequences.

At the beginning of this paper,we present several fundamental concepts and notations that will be used in the subsequent section.Let s(t)=s0,s1,···,sN−1be a sequence over a field GF(p),and p is an odd prime.The linear complexity or linear span of s(t)is defined to be the shortest positive integer l such that there are constants c0=1,c1,···,cl∈ GF(p)satisfying

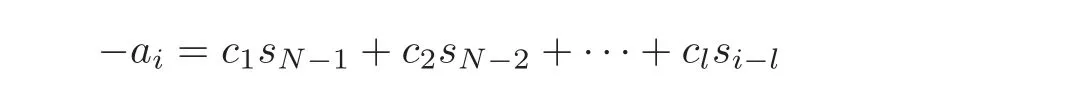
for all l≤ i≤ n

Such a polynomial c(x)=c0+c1x+c2x2+ ···+clxlis called the feedback polynomial of the shortest linear feedback shift register(LFSR for short)that generates s(t).

It is known that the feedback polynomial of s(t)is given by

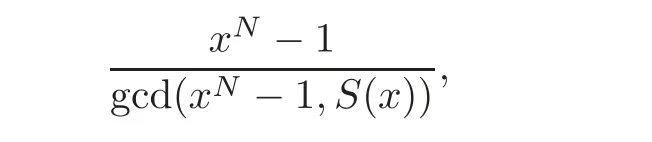
where

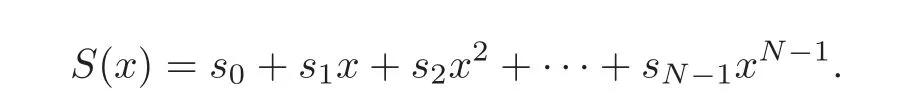
The linear complexity is calculated by

The rest of the paper is organized as follows.Section 2 will formally give the result of GF(p)linear complexities of the Hall’s sextic residues sequences,and the result of some cyclotomicset-based sequences will be given in Section 3.Section 4 summarizes our results and our future work.

2 Hall’s Sextic Residues Sequences

Let N=4u2+27=6f+1 be a prime and g be a primitive root modulo N.All the nonzero elements of the integers mod N can be partitioned into six residue classes Cl,l=0,1,···,5,as

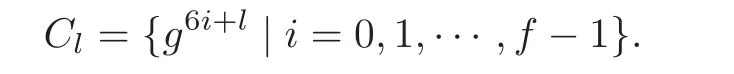
Hall’s sextic residue sequences with respect to the period N are defined as

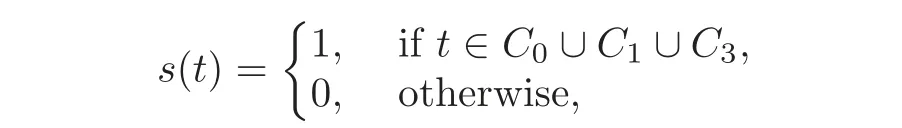
where t=0,1,···,N − 1.

Hall’s sextic residue sequences have a number of interesting properties,and we refer to[6–9]for details.Kim and Song[6]determined their GF(2)linear complexity and the characteristic polynomial.The trace representation of Hall’s sextic residue sequences of period N=7 mod 8 was given in[7].Dai etc.[8–9]explicitly described the trace representations of the binary sequences of the e-th(e ≤ 12)power residue cyclic difference sets,including the Hall’s sextic residue sequences.

For Hall’s sextic residue sequences with a period N,the corresponding S(x)is given by

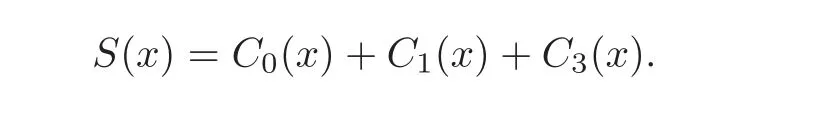
Then the linear complexity of a Hall’s sextic residue sequence s(t)(denoted by Lp(s))of the period N over GF(pm)is given by

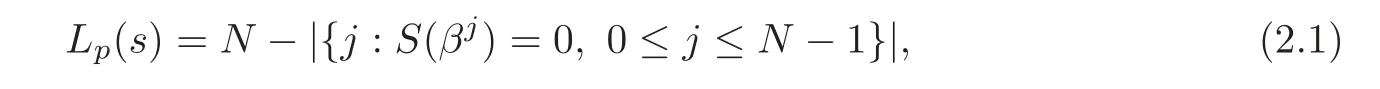
where β is a primitive N-th root of unity that is the splitting field of xN−1,and m can be determined by m=min{d|pd=1 mod N}.

In order to determine the linear complexity of Hall’s sextic residue sequences,we need the following two lemmas.

Lemma 2.1With respect to the above notation,we assume further thatN=−1 mod p.Letα,θ,γbe representing elements ofC0,C1,C2,respectively.Then

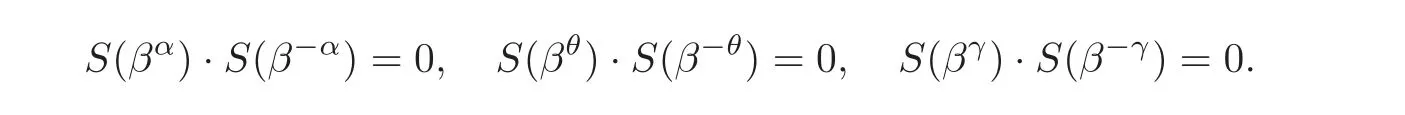
ProofWe first note that a Hall’s sextic residue sequence with a period N induces a cyclic Hadamard difference set D(v,k,λ)with parameters v=N,k=and λ =(see[10]).Consider that(−1)=(−1)2f=1 and N= −1 mod 4,so,−1∈ C3.Combining with the fact that D is a(v,k,λ)difference set,we have the following equation:

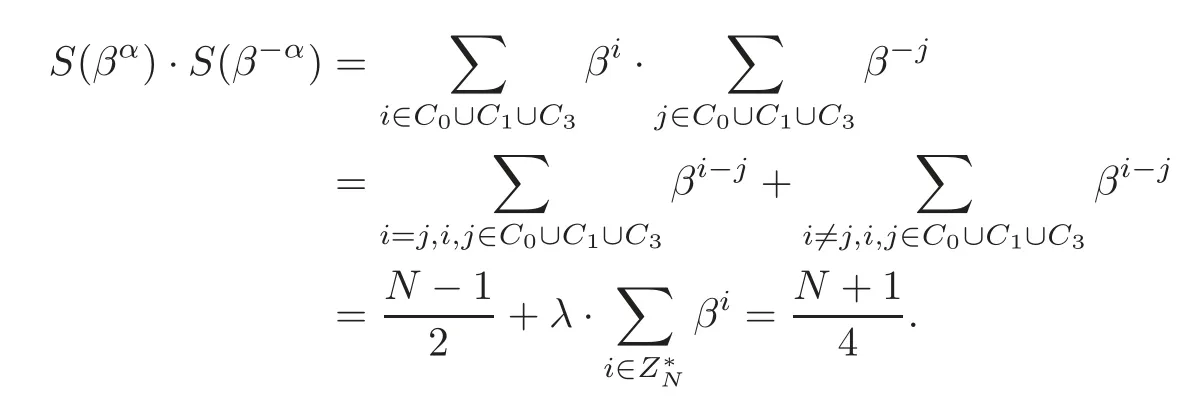
Evidently,if N=−1 mod p,we have

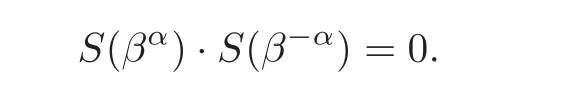
Similarly,S(βθ)·S(β−θ)=0,S(βγ)·S(β−γ)=0,so the lemma holds.

Lemma 2.2With respect to the above notation,we assume again thatN=−1 mod p,and then the equation

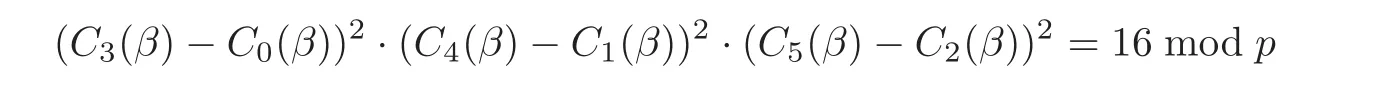
holds.

Lemma 2.2 can be conducted directly from the Theorem 1 in[11].That is,(C3(β) −C0(β))2·(C4(β)− C1(β))2·(C5(β)− C2(β))2=(−1)f+2·N ·M4.We know that the prime N can be uniquely expressed as 4N=L2+27M2if N=1 mod 3.For the Hall’s sextic residue sequences,M2=4.Noting that N=4u2+27,3f=2u2+13,f must be odd,and therefore,(C3(β)− C0(β))2·(C4(β)− C1(β))2·(C5(β)− C3(β))2=(−1)f+3·16 mod p=16 mod p.

The results of the GF(p)linear complexity are stated in the following theorem.

Theorem 2.1Lets(t)be the Hall’s sextic residue sequences of the periodNas before.Then theGF(p)linear complexityLp(s)is given as follows:

(1)IfN=−1 mod p,then

(2)Otherwise,

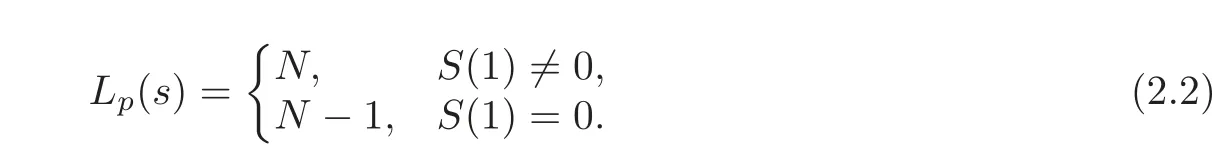
ProofThe proof of Theorem 2.1 is then completed by considering two cases depending on whether N=−1 mod p or not.

We first consider the case N=−1 mod p,which,according to Lemma 2.1,happens.It follows from Lemma 2.1 that S(βα) ·S(β−α)=0.By Lemma 2.2,it follows that either S(βα)=0 for all α ∈ C0,or S(β−α)=0 for all α ∈ C3.Clearly,the values of S(βα)and S(β−α)can not be 0 simultaneously.In this way,we can deduce that the values of S(βθ)and S(β−θ)can not be 0 at the same time and that is of S(βγ)and S(β−γ).Since S(1)=,it follows that S(1)=−1 mod p if N=−1 mod p.Hence,if N=−1 mod p,then by Lemma 2.1,

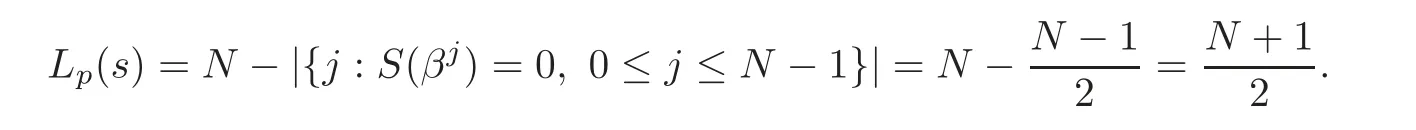
Secondly,we consider the case N−1 mod p.By Lemma 2.1,it follows that S(βα)·S(β−α)=0 mod p,which indicates that for all α ∈ C0∪ C3,S(βα)0.Similarly,we have that for all j∈ C1∪C4∪C2∪C5,S(βj)0.Thus,the linear complexity Lp(s)is N or N−1,which entirely depends on whether S(1)mod p is 0 or not.Here,we have completed the proof of the theorem.

3 Extension to Some Known Cyclotomic Diff erence Sets

In this section,we discuss how we can apply Lemma 2.1 to other binary sequences based on cyclotomic difference sets.In particular,we focus on some known cyclotomic difference sets,which were described in Table 1(see[12]).Note that the GF(p)linear complexity of Legendre sequecnes has been carefully studied in[5].Hence we focus on the following two cases:The quartic residue sequences and the 8-th power residue sequences.We omit the trivial cases for the 10-th power residue sequences,which only hold for the period N=31(see[8]).

Table 1 Some known cyclotomic difference sets

Allow us to give some notations firstly.Let N=ef+1 be a prime and g be a primitive root modulo N,and all the nonzero elements of the integers can be divided into e residue classes,l=0,1,···,f − 1,as

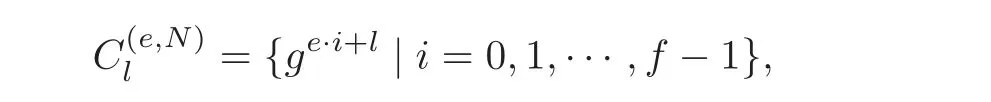
where e=4,8.

We define the quartic residue sequences and the 8-th power residue sequences as

With the goal of computing the GF(p)linear complexity,the issue is to decide the cardinality

3.1 The quartic residue sequences

In this subsection,Theorem 3.1 manifests our effort on the GF(p)linear complexity of the quartic residue sequences,while their GF(2)linear complexity was given in[8].In the following,we denoteas Clfor short,i.e.,Cl(x)=and S(x)=C0(x).

Theorem 3.1Lets(t)be the quartic residue sequences of the periodN,andN=4t2+1(tbeing odd)be prime.Then theGF(p)linear complexityLp(s)is given as follows:

(1)If3N=−1 mod p,thenLp(s)=

(2)Otherwise,

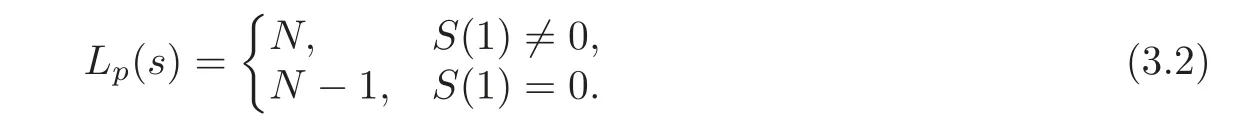
ProofThe quartic residue sequence with a period N induces a cyclic Hadamard difference set D(v,k,λ)with parameters v=N,k=and λ =.Consider that(−1)=1 mod N=1 and(−1)= −1 mod N,so,−1∈C2.Combining with the fact−1∈C2,it follows from Lemma 2.1 that C0(β)·C2(β)==0 mod p and C1(β)·C3(β)=

To finish the proof,notice the fact:(C0(β)−C2(β))2=(C0(β)+C2(β))2−4·C0(β)·C2(β)=(C0(β)+C2(β))2,and(C1(β)−C3(β))2=(C1(β)+C3(β))2.It follows that(C0(β)−C2(β))2·(C1(β)− C3(β))2=(C0(β)+C2(β))2·(C1(β)+C3(β))2.

We observe that C0∪C2,C1∪C3constitutes the quadratic and non-quadratic residue sets modulo N,respectively.Based on the two classical facts(see[13]):C0(β)+C2(β)+C1(β)+C3(β)= −1 and(C0(β)+C2(β)− C1(β)− C3(β))2=·N,it follows that(C0(β)− C2(β))2·(C1(β)− C3(β))2=mod p.We seek a contradiction to show that0 mod p under the condition 3N=−1 mod p.This condition implies p3,indicating that p=3 only happens in the second case of the theorem.If N=1 mod p holds,then 3N=3 mod p and−1=3 mod p,which gives a contradiction.It is clear that the values of C0(β)and C2(β−1)can not be 0 at the same time.So are the values of C1(β)and C3(β).Moreover,C0(1)=0 mod p,that is,we prove the result.The second part of this theorem is easy to see.

3.2 The 8-th power residue sequences

In this subsection,we will present our result of the 8-th power residue sequences.Suppose that N=8t2+1=64u2+9=8f+1(t,u are odd).To simplify the description,we use Clto denoteand

Now,we elaborate on the details of the Theorem 3.2.

Theorem 3.2Lets(t)be the8-th power residue sequences of the periodN,andNbe prime as before.Then on theGF(p)linear complexity,Lp(s)is given as follows:

(1)If7N=−1 mod p,thenLp(s)=

(2)Otherwise,

ProofWe first consider the case under the condition 7N=−1 mod p.The 8-th power residue sequences guide an-cyclic hadamard difference set.Apparently,=1 mod N,while= −1 mod N,so,−1∈C4.Therefore,we have the following 4 equations,indicating that at least four of the total eight residue classes make C0(βj)=0:C0(β)·C0(β−1)=C0(β)·C4(β)==0,C1(β)·C5(β)=0,C2(β)·C6(β)=0,C3(β)·C7(β)=0.

For convenience,let D0,D1,D2,D3represent C0∪C4,C1∪C5,C2∪C6,C3∪C7,respectively.In order to prove the final result,we need to examine the value of(D0(β)·D2(β))·(D1(β)·D3(β)).First,we compute the values of D0(β)·D2(β),D1(β)·D3(β)by the cyclotomic numbers of order 4(see[14]),respectively.

where x=−3 in the case of N=64u2+9=x2+4y2,x=1 mod 4.

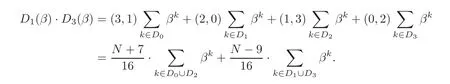
Observe that

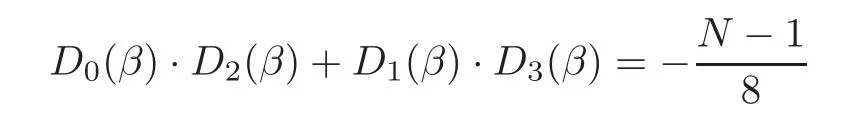
and

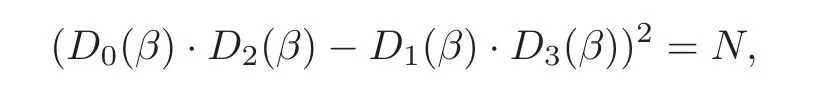
so

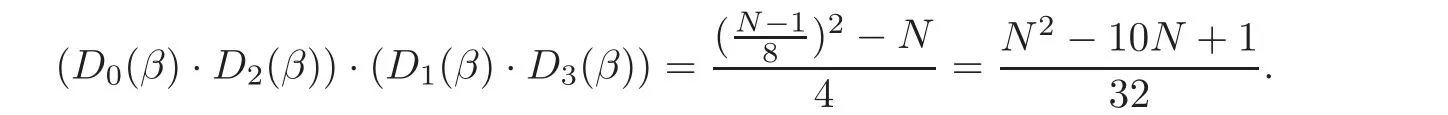
In the first case,7N=−1 mod p,which indicates that,so,

From the calculation of the value(D0(β)·D2(β))·(D1(β)·D3(β)),we know that there are four and only four of the total eight residue classes that make C0(βj)=0.In addition,mod p.Hence,the first part of the theorem holds.The second part of this theorem can be veri fied easily.

4 Discussions

In this paper,we give some results on the GF(p)linear complexities of Hall’s sextic residue sequences,and some known cyclotomic-difference-set-based sequences.These sequences share a common feature:The GF(p)linear complexity is as much as half of the sequence period N.From the view of practical use,any discussion of the GF(2)linear complexity requires a discussion of the GF(p)linear complexity for these binary sequences.A challenge is that the calculation of GF(p)linear complexity may be as difficult as or more difficult than developing the sequences themselves.

Unfortunately,despite that the GF(p)linear complexities of these known sequences have been determined,the feedback polynomial of these sequences has not been well addressed in this paper.Clearly,we are only interested in the sequences which are constructed based on the cyclic difference sets,but a plethora of sequences constructed by the cyclic almost difference sets(see[14])or the generalized cyclotomic sequences(see[15])on the GF(p)linear complexities are still open,which will be promising directions for future work.

AcknowledgementsThe authors wish to thank professor Hao Chen and professor Qin Yue for their patient discussions and constructive suggestions that considerably contributed to the fulfillment of this paper.

[1]Massey,J.L.,Shift-register synthesis and bch decoding,IEEE Transactions on Information Theory,15(1),1969,122–127.

[2]Klapper,A.,The vulnerability of geometric sequences based on fields of odd characteristic,Journal of Cryptology,7(1),1994,33–51.

[3]Chen,H.and Xu,L.,On the binary sequences with high gf(2)linear complexities and low gf(p)linear complexities,IACR Cryptology ePrint Archive,2005,2005,241.

[4]XU,L.Q.,On gf(p)-linear complexities of binary sequences,The Journal of China Universities of Posts and Telecommunications,16(4),2009.112–124.

[5]He,X.,On the gf(p)linear complexity of Legendre sequences,Journal on Communications,29(3),2008,16–22(in Chinese).

[6]Kim,J.H.and Song,H.Y.,On the linear complexity of halls sextic residue sequences,IEEE Transactions on Information Theory,47(5),2001,2094–2096.

[7]Kim,J.H.,Song,H.Y.and Gong,G.,Trace representation of Hall’s sextic residue sequences of period p ≡7(mod 8),Mathematical Properties of Sequences and Other Combinatorial Structures,Springer-Verlag,New York,2003,23–32.

[8]Dai,Z.,Gong,G.,Song,H.Y.and Ye,D.,Trace representation and linear complexity of binary e-th power residue sequences of period,IEEE Transactions on Information Theory,57(3),2011,1530–1547.

[9]Dai,Z.,Gong,G.and Song,H.Y.,Trace representation and linear complexity of binary e-th residue sequences,Proceedings of International Workshop on Coding and Cryptography,2003,24–28.

[10]Baumert,L.D.,Cyclic Diff erence Sets,Springer-Verlag,New York,1971.

[11]Lazarus,A.J.,The sextic period polynomial,Bulletin of the Australian Mathematical Society,49(2),1994,293–304.

[12]Colbourn,C.J.and Dinitz,J.H.,Handbook of Combinatorial Designs,CRC Press,Boca Raton,2010.

[13]Ireland,K.and Rosen,M.I.,A Classical Introduction to Modern Number Theory,Springer-Verlag,Boca Raton,1982.

[14]Ding,C.,Helleseth,T.and Lam,K.Y.,Several classes of binary sequences with three-level autocorrelation,IEEE Transactions on Information Theory,45(7),1999,2606–2612.

[15]Hu,L.,Yue,Q.and Wang,M.,The linear complexity of whitemans generalized cyclotomic sequences of period,IEEE Transactions on Information Theory,58(8),2012,5534–5543.