Geometrical Realization of Low-Dimensional Complete Intersections∗

Jianbo WANG Jianpeng DU

1 Introduction

Let⊂ CPn+rbe a smooth complete intersection of multidegree:=(d1,···,dr)and the product d1d2···dris called the total degree,denoted by d.The celebrated Lefschetz hyperplane section theorem asserts that the pairis n-connected.Thom showed that the complex dimension n and the multidegreedetermine the diffeomorphism type ofHowever,the multidegree is not a topological invariant.An interesting and challenging problem is to classify complete intersections by numerical topological invariants,such as the total degree,the Pontrjagin classes and the Euler characteristics,which usually are polynomials on the multidegree(see Section 2).

In dimension 1,the classification of complete intersections follows from the classical theory of Riemann surfaces.In dimension 3,appealing to general classification theorems in differential topology,the classification was established by Jupp[1]and Wall[2],while in dimension 2,the homeomorphism classification has been settled by Freedman[3].Ebeling[4]and Libgober-Wood[5]independently found examples of homeomorphic complex 2-dimensional complete intersections which are not diffeomorphic.In[6],Fang and Klaus proved that,in dimension n=4,two complete intersectionsandare homeomorphic if and only if they have the same total degree,Pontrjagin classes and Euler characteristics.Furthermore,Fang and the first author[7]generalized this homeomorphism result to dimensions n=5,6,7.

Theorem 1.1(see[6–7])Two complete intersectionsandare homeomorphic if and only if they have the same total degree,Pontrjagin classes and Euler characteristics,provided thatn=4,5,6,7.

With the help of Kreck’s modi fied surgery theory(see[8]),Traving[9]obtained partial classification results in higher dimensions under some restrictions on the total degree.Particularly,to the prime factorization of total degreeunder the assumption thatfor all primes p with p(p− 1)≤n+1,Traving proved the following result(see[8,Theorem A]or[9]).

Theorem 1.2(see[9])Two complete intersectionsandof a complex dimensionn>2fulfilling the assumption above for the total degree are diffeomorphic if and only if the total degrees,the Pontrjagin classes and the Euler characteristics agree.

It is well known all complete intersections of a fixed multidegree are diffeomorphic.On the other hand,there exist diffeomorphic complete intersections with different multi-degrees.For lower dimensions,such as complex dimensions 2,3,4,5,the diffeomorphic examples can be found in[10–13].

The aim of this paper is to give examples of diffeomorphic(or homeomorphic)complex n-dimensional complete intersections,mainly n7,which can be considered as a geometrical realization of the above Theorems 1.1–1.2.On the other hand,Libgober and Wood[13, §9]conjectured that there exist the diffeomorphic complex 3-dimensional complete intersections with different first Chern classes,which give an example of a disconnected moduli space.In this paper,the above conjecture will be con firmed by one of the listed examples.

These examples were partially found by computer searching.Note that,according to[13,Proposition 7.3],if Xn(d1,···,dr)⊂ CPn+rsatisfies n>2 and,then the total degree and Pontrjagin classes of Xn(d1,···,dr)determine the multidegree.Thus,it is impossible to find out such a homeomorphic or diffeomorphic example,in which the codimension r is small relative to the complex dimension n.It is worth stating that the degrees and codimensions in our examples will be as small as possible.

2 Characteristic Classes of Complete Intersections

For a complete intersection Xn(d),let H be the restriction of the dual bundle of the canonical line bundle over CPn+rto,andAssociate the multidegree=(d1,d2,···,dr)and define the power sumsThen the Chern classes,Pontrjagin classes and Euler characteristic are presented as follows(see[13]):

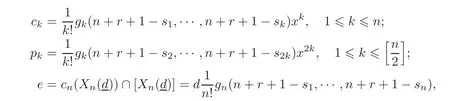
where gk(k≥1)are the polynomials with k indeterminates(s1,s2,···,sk)that can be iteratively computed from the Newton formula:

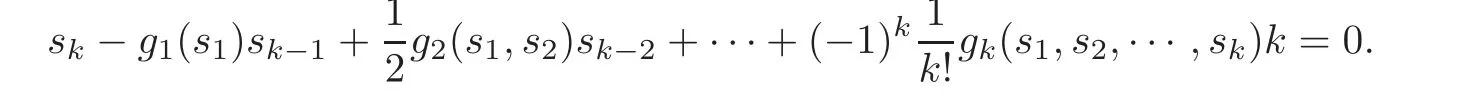
For example,here are the first seven gk’s.

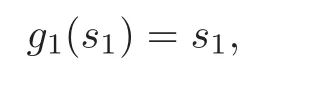
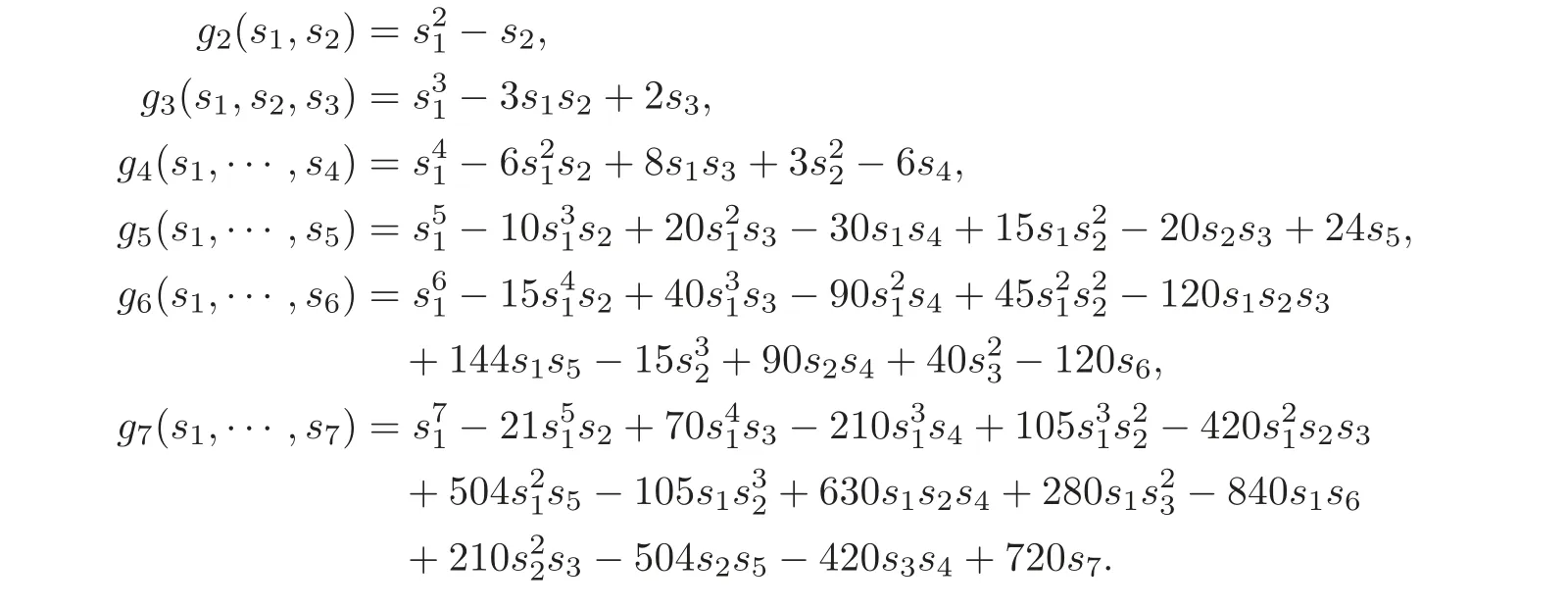
Note that the kthChern class ckand the Pontrjagin class pkare integral multiples of xkand x2k,so we can compare these invariants for different complete intersections.For convenience,throughout the rest of the paper,the Chern class ckand the Pontrjagin class pkofare viewed as the multiples of xkand x2k,respectively.

3 Examples of Diff eomorphic(Homeomorphic)Low-Dimensional Complete Intersections

In this section,some examples of diffeomorphic or homeomorphic complex n-dimensional complete intersections will be listed for n=2,3,···,7,and one of the examples will con firm the conjecture of Libgober and Wood[13,§9].

3.1 Complex 2-dimensional complete intersections

For the complex 2-dimensional complete intersection X2(d1,···,dr),the total degree,the first Chern class,the Pontrjagin class and the Euler characteristic are as follows:

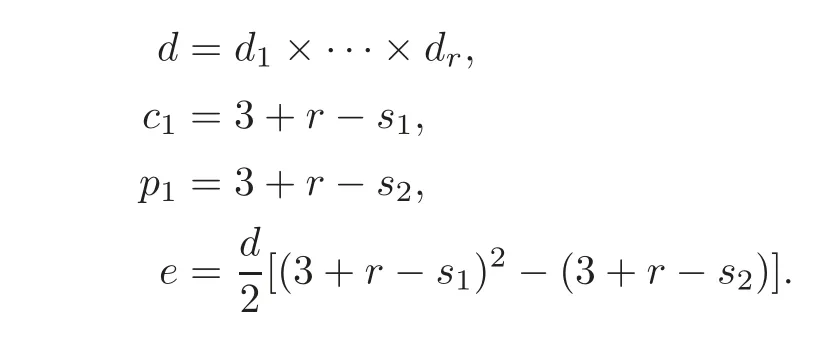
Theorem 3.1(see[4])Two complete intersectionsX2(d1,···,dr)andX2(,···,are homeomorphic,if and only if

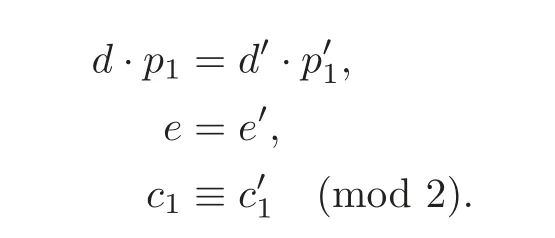
Theorem 3.1 is basically due to Freedman’s celebrated work on the topology of 4 manifolds(see[3]),which implies that the homeomorphism type of complex 2-dimensional complete intersections is determined by its intersection form.A more detailed description can be found in[4].

Two homeomorphic complete intersectionsandwithwill give an example of homeomorhpic but non-diffeomorphic complex 2-dimensional complete intersections(see[4–5]).Note that Ebeling[4]and Libgober-Wood[5]independently found that X2(10,7,7,6,6,3,3)and X2(9,5,3,3,3,3,3,2,2)are homeomorphic but not diffeomorphic.Here,some other examples with lower codimensions are listed.

Example 3.1The following invariants give seven examples of pairs of complex 2-dimensional complete intersections which are homeomorphic but not diffeomorphic.The two smoothings in each pair have distinct c1’s.

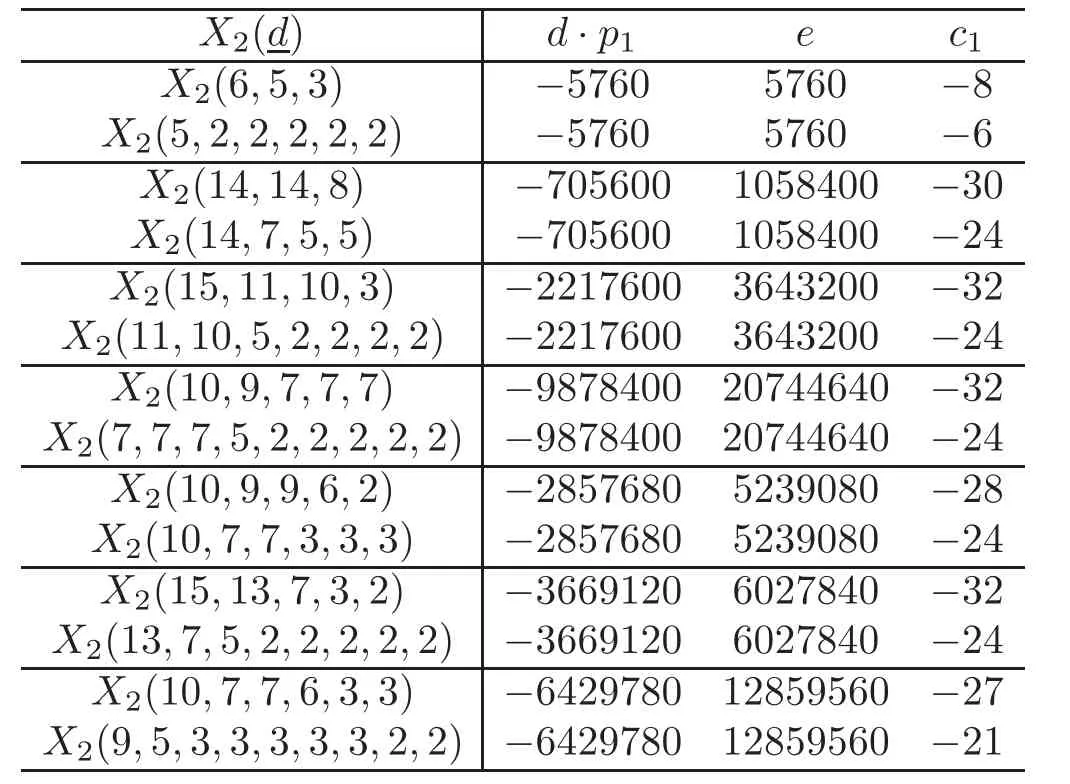
Table 1 Homeomorphic but non-diffeomorphic 2-dimensional complete intersections

3.2 Complex 3-dimensional complete intersections

For a complex 3-dimensional complete intersection X3(d1,···,dr),the related topological characteristic classes are as follows:

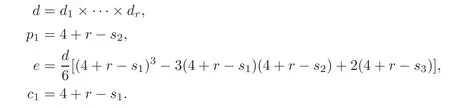
Theorem 3.2(see[1–2])Two complex3-dimensional complete intersections are diffeomorphic,if and only if they have the same total degreed,the first Pontrjagin classp1and the Euler characteristice.

In[13,§9],Libgober and Wood conjectured that there exist such examples of diffeomorphic complex 3-dimensional complete intersections with different first Chern classes,which would give an example of a disconnected moduli space.Brückmann[10]showed that there exist the diffeomorphic complex 3-dimensional complete intersections belonging to components of the moduli space of different dimensions,but with the same first Chern classes.In the following,some examples of diffeomorphic complex 3-dimensional complete intersections will be listed,and the conjecture in[13]is con firmed by Table 3.

Example 3.2The following invariants give some pairs of diffeomorphic complex 3-dimensional complete intersections,where the ones with different first Chern classes c1’s give an example of a disconnected moduli space.

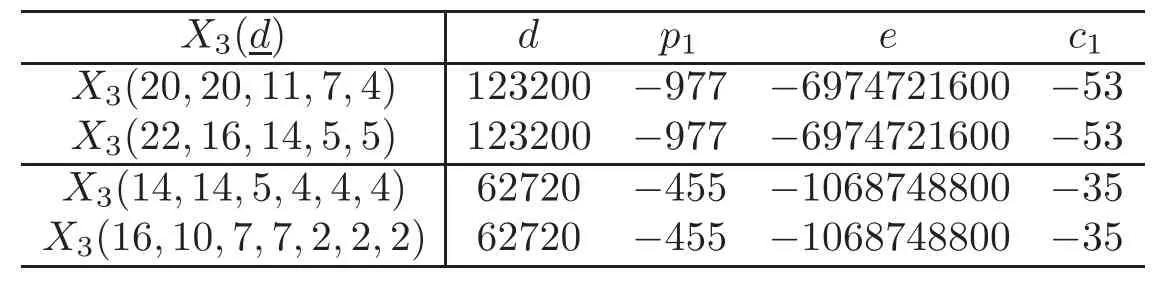
Table 2 Diff eomorphic 3-dimensional complete intersections with the same c1

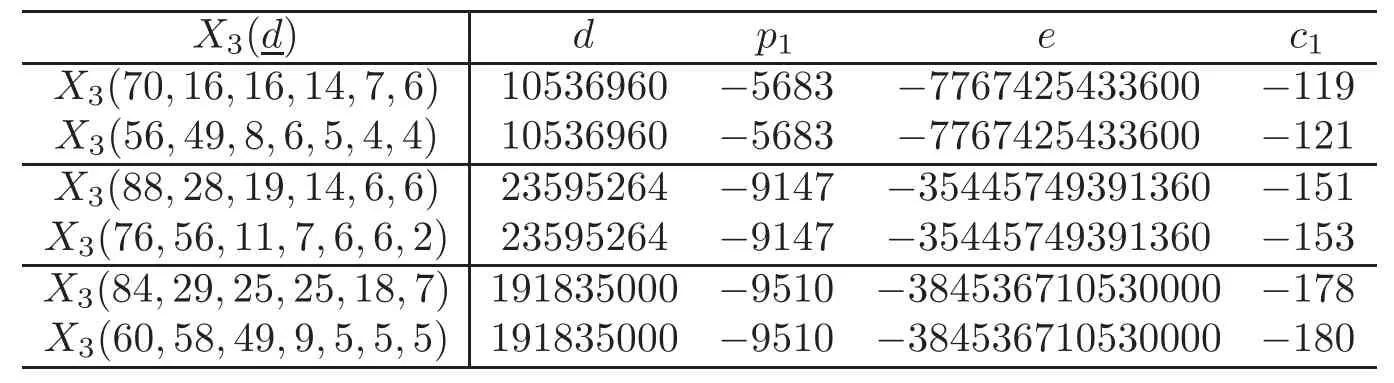
Table 3 Diff eomorphic 3-dimensional complete intersections with different c1’s

3.3 Complex 4-dimensional complete intersections

For a complex 4-dimensional complete intersection X4(d1,···,dr),we have the following invariants:

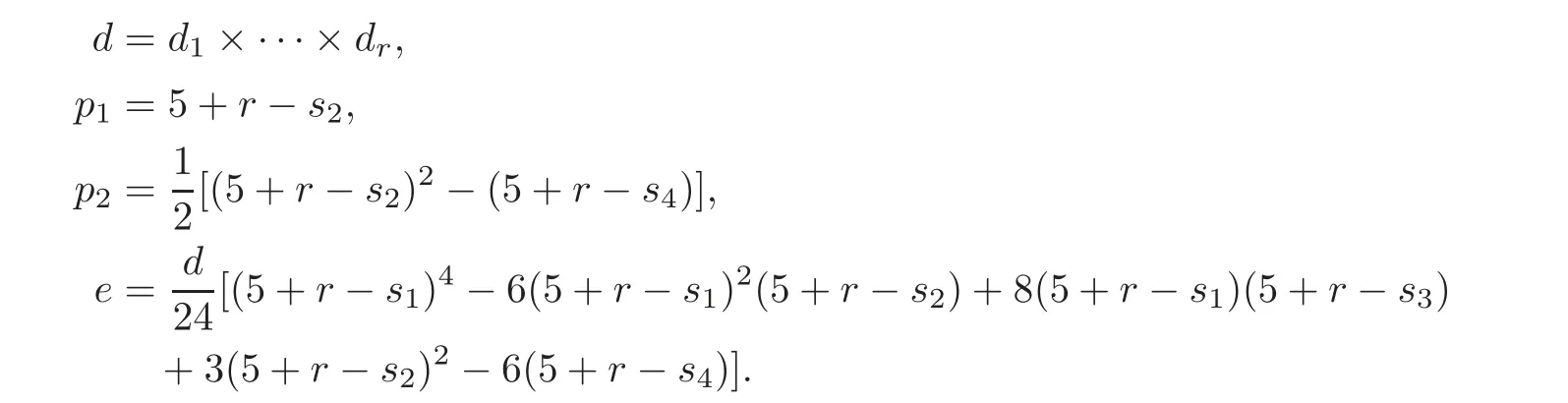
According to Theorem 1.2,to construct homeomorphic complex 4-dimensional complete intersections,we need to find out two different multi-degrees to satisfy that the above invariants all agree.Furthermore,by Theorem 1.2,if ν2(d)>5.5,then the homeomorphic 4-dimensional complete intersections are diffeomorphic.

Example 3.3Table 4 gives two pairs of homeomorphic complex 4-dimensional complete intersections.

Table 4 Homeomorphic 4-dimensional complete intersections

Example 3.4Table 5 gives two pairs of diffeomorphic complex 4-dimensional complete intersections,since the total degrees satisfy

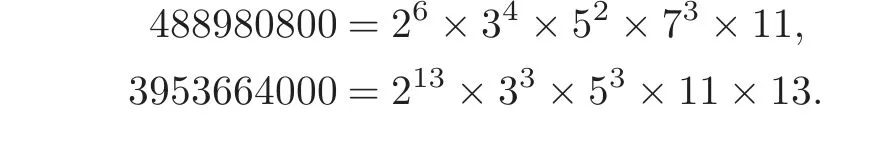
Table 5 Diff eomorphic 4-dimensional complete intersections

3.4 Complex 5-dimensional complete intersections

For a complex 5-dimensional complete intersection X5(d1,···,dr),we have the following invariants:

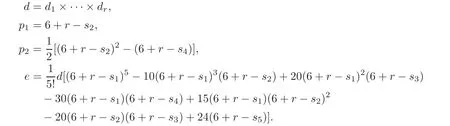
Two complex 5-dimensional complete intersections with the same d,p1,p2,e are homeomorphic.Furthermore,by Theorem 1.2,if ν2(d)≥6.5 and ν3(d)≥3.75,then they will be diffeomorphic.

Example 3.5Consider the following Table 6.

If the two pairs of multi-degrees have the same power sums s1,···,s5and the total degree d,then it is easily deduced that the corresponding complex 5-dimensional complete intersections have the same Pontrjagin classes and the Euler characteristics.Since the total degrees have the following prime factorization,

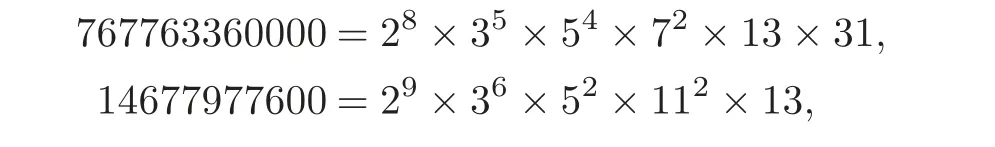
the corresponding two pairs of complete intersections are diffeomorphic.

Table 6 Diff eomorphic 5-dimensional complete intersections

Example 3.6The following table gives diffeomorphic complete intersections with distinct codimensions,where the diffeomorphism comes from the prime factorization of the total degree:d=104626080000=28×37×54×13×23.

Table 7 Diff eomorphic 5-dimensional complete intersections with distinct codimensions

3.5 Complex 6-dimensional complete intersections

For a complex 6-dimensional complete intersection X6(d1,···,dr),the related topological characteristic classes are as follows:

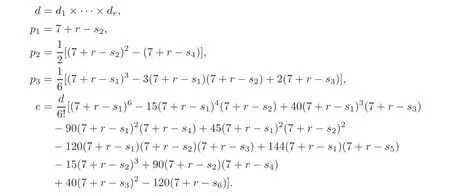
Two complex 6-dimensional complete intersections with the same d,p1,p2,p3,e are homeomorphic.Furthermore,by Theorem 1.2,if ν2(d)≥7.5 and ν3(d)≥4.25,then they will be diffeomorphic.

Example 3.7Consider the following two multi-degrees1The multi-degrees in Examples 3.7 and 3.9 were introduced by Guo Xianqiang on a mathematical BBS:http://bbs.emath.ac.cn/thread-5853-1-1.html.:

They have the same total degree d and power sums s1,···,s7:

Then the corresponding two complete intersections have the same total degree,Pontrjagin classes and Euler characteristics,so they are homeomorphic.Since the total degree has the prime factorization d=219×35×54×112×132×19×29×59,the corresponding two complete intersections

are diffeomorphic.

3.6 Complex 7-dimensional complete intersections

For a complex 7-dimensional complete intersection X7(d1,···,dr),the related topological characteristic classes are as follows:

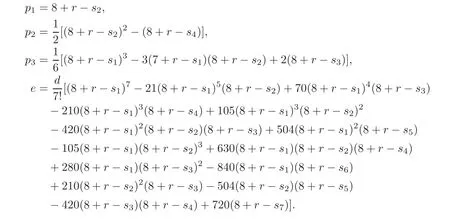
Two complex 7-dimensional complete intersections with the same d,p1,p2,p3,e are homeomorphic.Furthermore,by Theorem 1.2,if ν2(d)≥8.5 and ν3(d)≥4.75,then they will be diffeomorphic.

Example 3.8Consider the multi-degrees in Example 3.7,it is evident that the corresponding two 7-dimensional complete intersections have the same total degree,Pontrjagin classes and Euler characteristics.Thus complete intersections

are diffeomorphic by Theorem 1.2.

Example 3.9Consider the following two multi-degrees:

They have the same total degree d and power sums:s1,···,s7:

Furthermore,ν2(d)=28 and ν3(d)=13,so the corresponding two complete intersections

are diffeomorphic.

Example 3.10For the following two multi-degrees2These two multi-degrees firstly appeared in http://www.emath.ac.cn/ florilegium/r011n30.htm by Guo Xianqiang.:

they have the same total degree d and power sums s1,···,s11:

Then the corresponding two complete intersections are homeomophic.Since ν2(d)=51 and ν3(d)=18,the corresponding two complete intersections

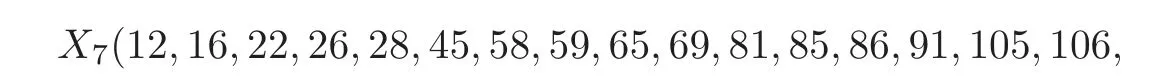
are diffeomorphic.

Remark 3.1Note that,just like Examples 3.7–3.8,for the multi-degrees that appeared in Subsection 3.6,the corresponding complex 6-dimensional complete intersections are also diffeomorphic.

Remark 3.2For higher-dimensional complete intersections,e.g.,n=8,9,10,11,multidegrees in Example 3.10 are still valid to satisfy that the n-dimensional complete intersections have the same total degree,Pontrjagin classes and Euler characteristic.However,because of the unknown classifications of complete intersections for higher dimensions,we can not give more examples of diffeomorphic or homeomorphic complete intersections.

AcknowledgementThe first author would like to thank Guo Xianqiang for his valuable and helpfuldiscussions.

[1]Jupp,P.,Classification of certain 6-manifolds,Proc.Cambridge Philos.Soc.,73,1973,293–300.

[2]Wall,C.T.C.,Classification problems in differential topology.On certain 6-manifolds,Invent.Math.,1,1966,355–374.

[3]Freedman,M.,The topology of four-dimensional manifolds,J.Diff erential Geom.,17,1982,357–453.

[4]Ebeling,W.,An example of two homeomorphic,nondiffeomorphic complete intersection surfaces,Invent.Math.,99(3),1990,651–654.

[5]Libgober,A.S.and Wood,J.W.,Uniqueness of the complex structure on Kähler manifolds of certain homotopy types,J.Diff erential Geom.,32(1),1990,139–154.

[6]Fang,F.Q.and Klaus,S.,Topological classification of 4-dimensional complete intersections,Manuscript Math.,90,1996,139–147.

[7]Fang,F.Q.and Wang,J.B.,Homeomorphism classification of complex projective complete intersections of dimensions 5,6 and 7,Math.Z.,266,2010,719–746.

[8]Kreck,M.,Surgery and duality,Ann.of Math.,149(3),1999,707–754.

[9]Traving,C.,Klassification vollständiger Durchschnitte,Diplomarbeit,Mainz,1985,http://www.info.de/Sta ff/traving.pdf

[10]Brückmann,P.,A remark on moduli spaces of complete intersections,J.Reine Angew.Math.,476,1996,209–215.

[11]Brückmann,P.,A remark on moduli spaces of 4-dimensional complete intersections,J.Reine Angew.Math.,525,2000,213–217.

[12]Wang,J.B.,Remarks on 5-dimensional complete intersections,Electron.Res.Announc.Math.Sci.,21,2014,28–40.

[13]Libgober,A.S.and Wood,J.W.,Diff erentiable structures on complete intersections,I,Topology,21,1982,469–482.