Exact Controllability with Internal Controls for First-Order Quasilinear Hyperbolic Systems with Zero Eigenvalues

Kaili ZHUANG

1 Introduction

Consider the following first-order quasilinear hyperbolic system:

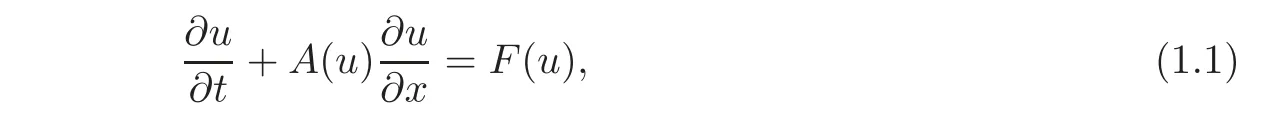
where u=(u1,···,un)Tis the unknown vector function of(t,x),A(u)is a given n× n matrix with suitably smooth components aij(u)(i,j=1,···,n),F(u)=(f1(u),···,fn(u))Tis a smooth vector function of u and

By hyperbolicity,on the domain under consideration,the matrix A(u)has n real eigenvalues λi(u)(i=1,···,n)and a complete set of left eigenvectors li(u)=(li1(u),···,lin(u))(i=1,···,n):

with

Suppose that there are no zero eigenvalues,namely,on the domain under consideration we have

For general first-order quasilinear hyperbolic systems with general nonlinear boundary conditions,Li Tatsien et al.[1–4]proposed a constructive method to establish the local exact boundary controllability by means of boundary controls.Since the speed of wave propagation is finite,the control time T>0 can not be too short.However,in many practical problems,we always hope to reduce the control time.For this purpose,Zhuang Kaili,Li Tatsien and Rao Bopeng[7]added some suitable internal controls,and established the local exact controllability in a shorter time by using the combined effect of boundary controls and internal controls.

In this paper,we will discuss the quasilinear hyperbolic system(1.1)with zero eigenvalues.Assume that on the domain under consideration,the eigenvalues of A(u)satisfy the following condition:

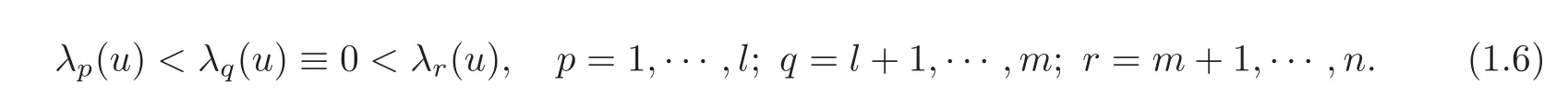
Consider the simplest equation with zero eigenvalue

It is easy to see that the exact controllability cannot be achieved only by boundary controls.Therefore,different from the situation that the eigenvalues satisfy(1.5),in order to realize the exact controllability for quasilinear hyperbolic systems with zero eigenvalues,we should use not only suitable boundary controls but also suitable internal controls.For general first-order quasilinear hyperbolic systems with zero eigenvalues together with the general nonlinear boundary conditions,by using boundary controls and adding internal controls to a part of equations corresponding to zero eigenvalues,Li Tatsien and Yu Lixin[5],Zhang Qi[6]established the corresponding local exact controllability.At this time,the control time T>0 should be suitably large,too.

In the present paper,we try to input some suitable internal controls to reduce the control time.To this end,it is necessary to rewrite the system(1.1)into the corresponding characteristic form

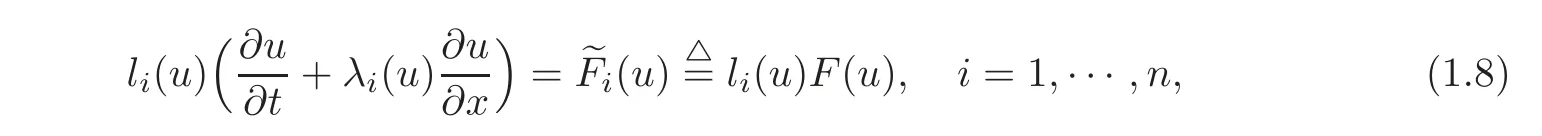
in which the i-th equation consists of only the directional derivative of the unknown function u with respect to t along the i-th characteristic direction=λi(u),and

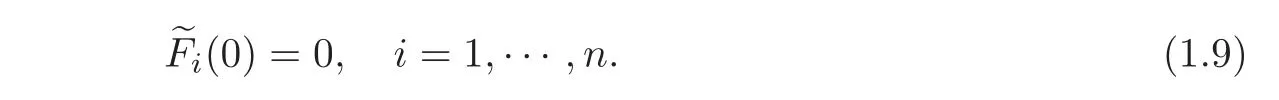
Adding suitable internal controls ci(t,x)(i=1,···,n)to(1.8),we have

where

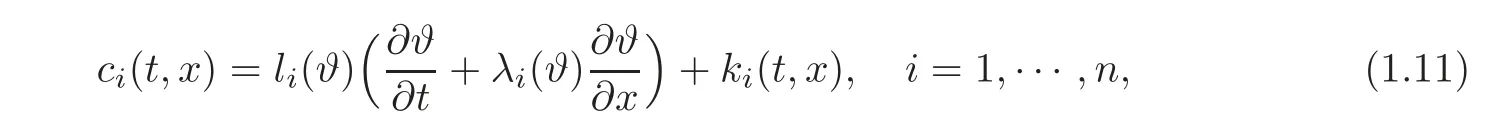
in which ϑ = ϑ(t,x)is a C1vector function of(t,x)and ki(t,x)(i=1,···,n)are C1functions of(t,x).

Let

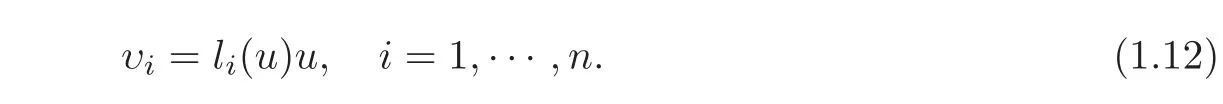
We consider the mixed initial-boundary value problem for the quasilinear hyperbolic system(1.10)with the initial condition

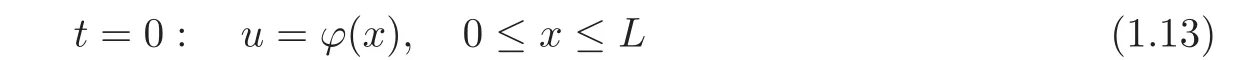
and the following boundary conditions:

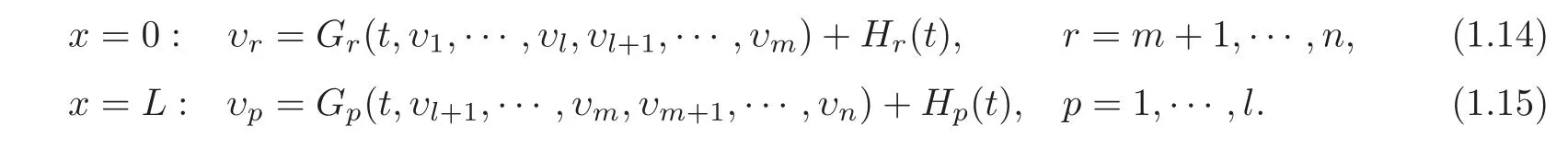
Without loss of generality,we assume that

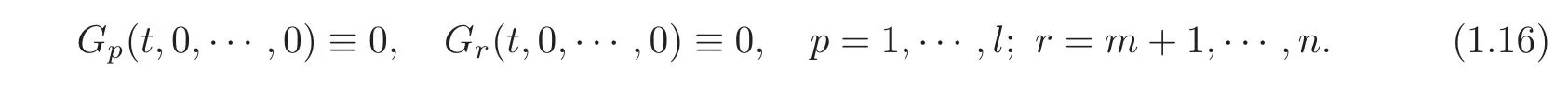
For any given initial data ϕ and final data ψ with small C1[0,L]norm,if there exists a T>0 such that,taking Hp,Hr(p=1,···,l;r=m+1,···,n)or a part of Hp,Hr(p=1,···,l;r=m+1,···,n)as boundary controls and ci(t,x)(i=1,···,n)as internal controls,the corresponding mixed initial-boundary value problem(1.10)and(1.13)–(1.15)admits a unique C1solution u=u(t,x)with small C1norm on the domain R(T)={(t,x)|0≤t≤T,0≤x≤L},which satisfies exactly the final condition

or

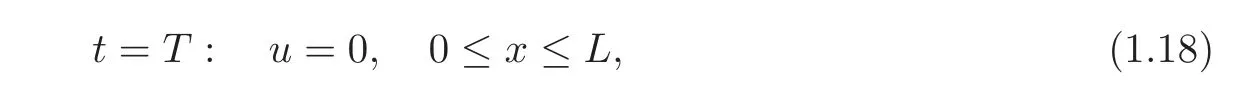
then we say that the mixed initial-boundary value problem(1.10)and(1.13)–(1.15)possesses the local exact controllability or the local exact null controllability,respectively.

2 Local Exact Controllability with Boundary Controls and Internal Controls

Theorem 2.1(Local Two-Sided Exact Controllability)Assume thatλi(u),li(u),(u),Gp(t,·),andGr(t,·)(i=1,···,n;p=1,···,l;r=m+1,···,n)are allC1functions with respect to their arguments.Assume furthermore that(1.6),(1.9)and(1.16)hold.For any givenδ(0< δ<),ifthen for any given initial dataϕand final dataψwith smallC1[0,L]norm,there exist boundary controlsHp,Hr(p=1,···,l;r=m+1,···,n)with smallC1[0,T]norm and internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the mixed initial-boundary value problem(1.10)and(1.13)–(1.15)admits a uniqueC1solutionu=u(t,x)with smallC1norm on the domainR(T),which satisfies exactly the final condition(1.17).

To prove Theorem 2.1,we construct the following system of the characteristic form:

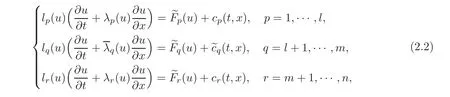
where(t,x)(i=1,···,n)are the corresponding internal controls and

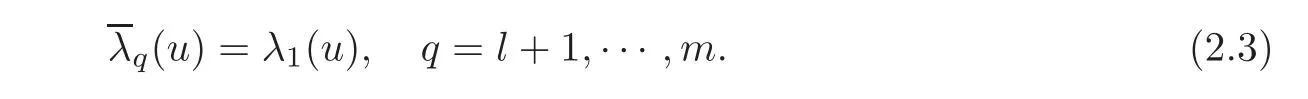
Obviously,(2.2)is a system without zero eigenvalues.Corresponding to(2.3),we give the following artificial boundary conditions:

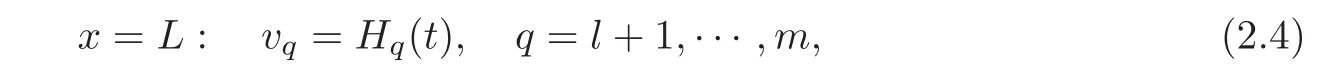
in which Hq(t)(q=l+1,···,m)are C1functions of t.

For the mixed initial-boundary value problem(2.2),(1.13)–(1.15)and(2.4),according to the result on local two-sided exact controllability in[7],we have the lemma.

Lemma 2.1Under the hypotheses of Theorem2.1,suppose furthermore that(2.3)holds.LetT>0be defined by(2.1).For any given initial dataϕand final dataψwith smallC1[0,L]norm,there exist boundary controlsHi(i=1,···,n)with smallC1[0,T]norm and internal controls

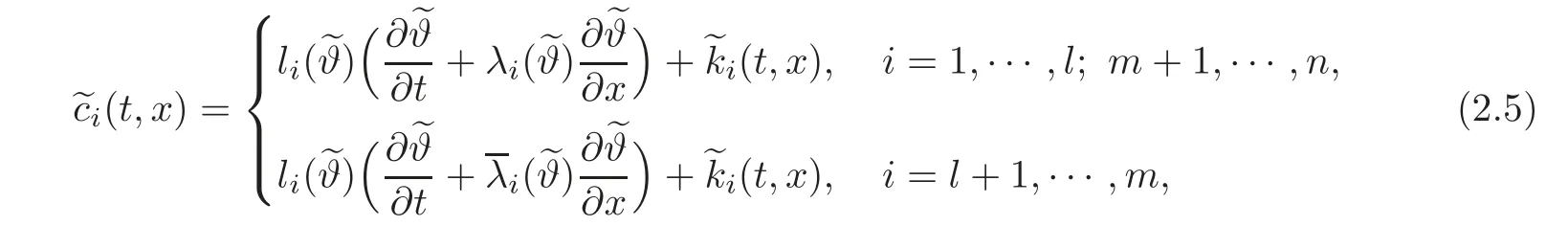
in which theC1[R(T)]norm ofand(i=1,···,n)is suitably small,such that the mixed initial-boundary value problem(2.2),(1.13)–(1.15)and(2.4)admits a uniqueC1solutionu=u(t,x)with smallC1norm on the domainR(T),which satisfies exactly the final condition(1.17).

By Lemma 2.1,we can prove Theorem 2.1.

In fact,substituting the C1solution u=u(t,x)given by Lemma 2.1 into boundary conditions(1.14)–(1.15),we get the desired boundary controls:

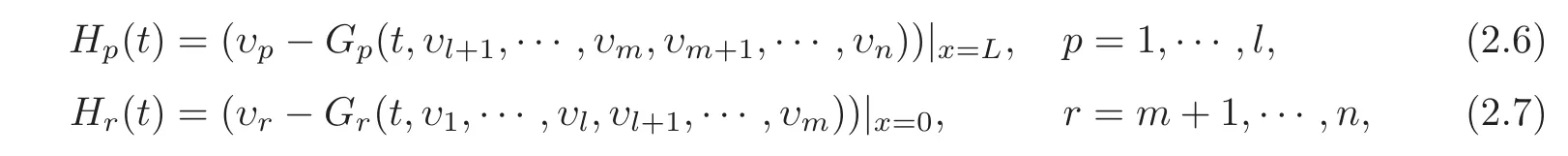
where υi(i=1,···,n)are defined by(1.12): υi=li(u(t,x))u(t,x)(i=1,···,n).Noting(1.16),the C1norm of Hpand Hr(p=1,···,l;r=m+1,···,n)is suitably small.On the other hand,substituting u=u(t,x)into system(1.10),we get the desired internal controls

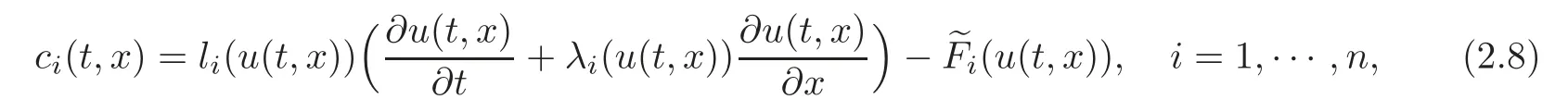
which correspond to(1.11)with

Noting(1.9),the C1[R(T)]norm of ϑ and ki(i=1,···,n)is also small.Thus,we obtain the desired exact controllability.

Theorem 2.2(Local One-Sided Exact Controllability)Under the hypotheses of Theorem2.1,suppose furthermore that the number of the positive eigenvalues is not greater than that of negative ones:

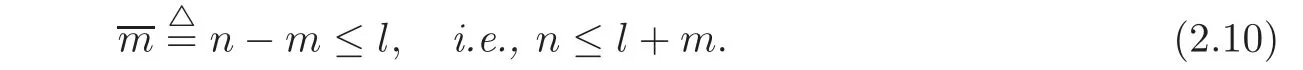
Suppose finally that in a neighborhood ofu=0,the boundary conditions(1.14)onx=0can be equivalently rewritten as

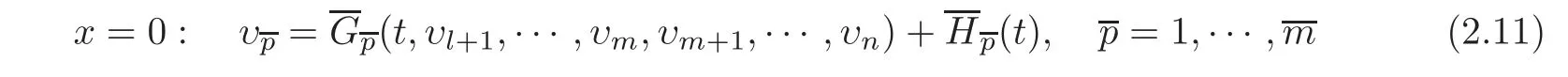
with

Then

For any givenδ(0< δ<),if

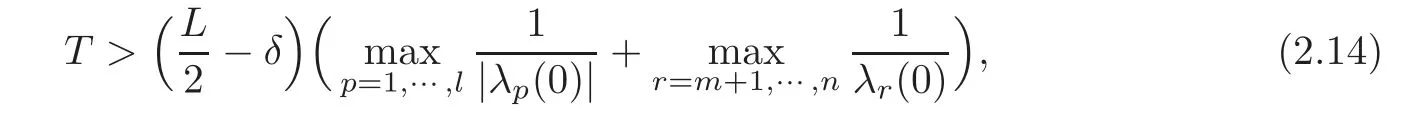
then for any given initial dataϕand final dataψwith smallC1[0,L]norm,and any givenHr(r=m+1,···,n)with smallC1[0,T]norm,such that the conditions ofC1compatibility are satisfied at the points(t,x)=(0,0)and(T,0),respectively,there exist boundary controlsHp(p=1,···,l)with smallC1[0,T]norm and internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the conclusion of Theorem2.1holds.

To prove Theorem 2.2,we construct the characteristic system(2.2),where(t,x)(i=1,···,n)are the corresponding internal controls and(u)(q=l+1,···,m)are given by(2.3).Obviously,(2.2)is a system without zero eigenvalues.Corresponding to(2.3),we give the artificial boundary conditions(2.4)on x=L,in which Hq(t)(q=l+1,···,m)are C1functions of t.

For the mixed initial-boundary value problem(2.2),(1.13)–(1.15)and(2.4),according to the result on local one-sided exact controllability in[7],we have Lemma 2.2.

Lemma 2.2Under the hypotheses of Theorem2.2,suppose furthermore that(2.3)holds.LetT>0be defined by(2.14).For any given initial dataϕand final dataψwith smallC1[0,L]norm,and any givenHr(r=m+1,···,n)with smallC1[0,T]norm,such that the conditions ofC1compatibility are satisfied at the points(t,x)=(0,0)and(T,0),respectively,there exist boundary controlsHpandHq(p=1,···,l;q=l+1,···,m)with smallC1[0,T]norm and internal controls(t,x)(i=1,···,n)given by(2.5),in which theC1[R(T)]norm ofand(i=1,···,n)is suitably small,such that the conclusion of Lemma2.1holds.

By Lemma 2.2,we can prove Theorem 2.2.

In fact,substituting the C1solution u=u(t,x)given by Lemma 2.2 into boundary conditions(1.15),we get the desired boundary controls Hp(t)(p=1,···,l)given by(2.6),where υi(i=1,···,n)are defined by(1.12).Noting(1.16),the C1norm of Hp(p=1,···,l)is suitably small.On the other hand,substituting u=u(t,x)into the system(1.10),we get the desired internal controls ci(t,x)(i=1,···,n)given by(2.8),which correspond to(1.11)with(2.9).Noting(1.9),the C1[R(T)]norm of ϑ and ki(i=1,···,n)is also small.Thus,we obtain the desired exact controllability.

Theorem 2.3(Local Two-Sided Exact Controllability with Less Controls)Under the hypotheses of Theorem2.1,suppose furthermore that the number of positive eigenvalues is less than that of negative ones:

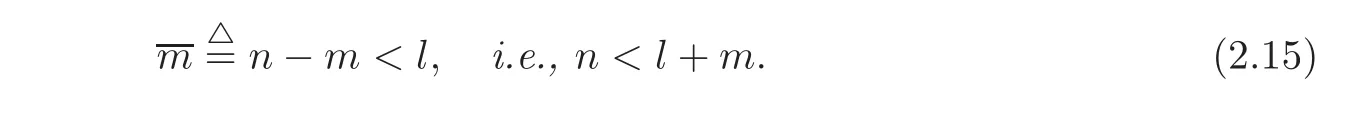
Suppose finally that in a neighborhood ofu=0,without loss of generality,the firstmboundary conditions in(1.15),namely,

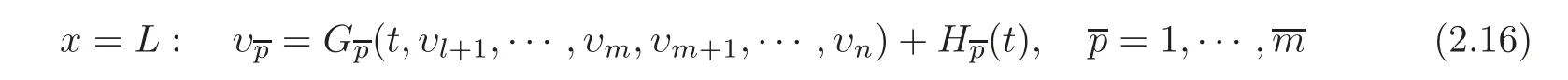
can be equivalently rewritten as

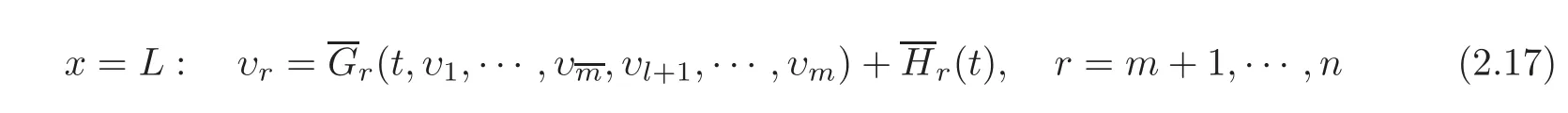
with

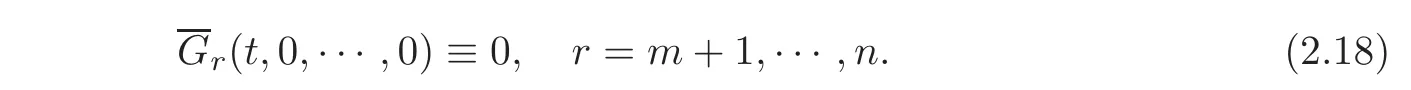
Then

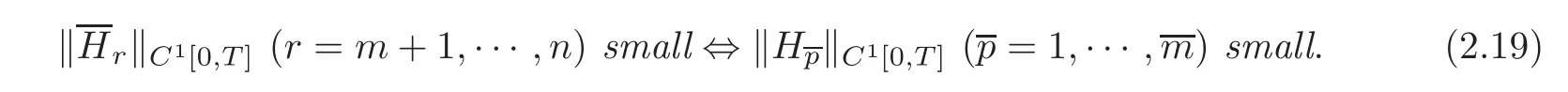
For any givenδ(0< δ<,ifT>0satisfies(2.14),then for any given initial dataϕand final dataψwith smallC1[0,L]norm,and for any givenwith smallC1[0,T]norm,such that the corresponding conditions ofC1compatibility are satisfied at the points(t,x)=(0,L)and(T,L),respectively,there exist boundary controlsandHr1,···,l;r=m+1,···,n)with smallC1[0,T]norm and internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the conclusion of Theorem2.1holds.

To prove Theorem 2.3,we also construct the characteristic system(2.2)without zero eigenvalues,where(t,x)(i=1,···,n)are the corresponding internal controls and(u)(q=l+1,···,m)are given by(2.3).Corresponding to(2.3),we give the artificial boundary conditions(2.4)on x=L,in which Hq(t)(q=l+1,···,m)are C1functions of t.

For the mixed initial-boundary value problem(2.2),(1.13)–(1.15)and(2.4),according to the result on local two-sided exact controllability with less controls in[7],we have the following lemma.

Lemma 2.3Under the hypotheses of Theorem2.3,suppose furthermore that(2.3)holds.LetT>0be defined by(2.14).For any given initial dataϕand final dataψwith smallC1[0,L]norm,and any givenHp(=1,···,)with smallC1[0,T]norm,such that the conditions ofC1compatibility are satisfied at the points(t,x)=(0,L)and(T,L),respectively,there exist boundary controlsandHr+1,···,l;q=l+1,···,m;r=m+1,···,n)with smallC1[0,T]norm and internal controls(t,x)(i=1,···,n)given by(2.5),in which theC1[R(T)]norm ofand(i=1,···,n)is suitably small,such that the conclusion of Lemma2.1holds.

By Lemma 2.3,we can prove Theorem 2.3.

In fact,substituting the C1solution u=u(t,x)given by Lemma 2.3 into boundary conditions(1.14)and the last l−m=l+m−n boundary conditions in(1.15),we get the desired boundary controls:

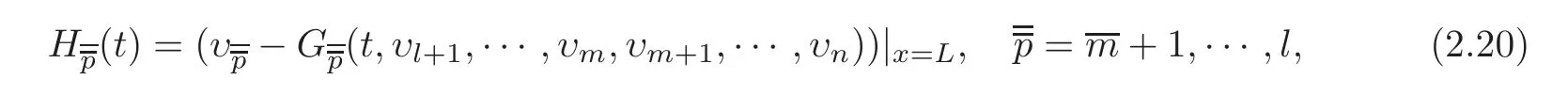
and Hr(r=m+1,···,n)given by(2.7),where υi(i=1,···,n)are defined by(1.12).Noting(1.16),the C1norm of Hpand Hr(+1,···,l;r=m+1,···,n)is suitably small.On the other hand,substituting u=u(t,x)into system(1.10),we get the desired internal controls ci(t,x)(i=1,···,n)given by(2.8),which corresponds to(1.11)with(2.9).Noting(1.9),the C1[R(T)]norm of ϑ and ki(i=1,···,n)is also small.Thus,we obtain the desired exact controllability.

3 Local Exact Null Controllability with Boundary Controls and Internal Controls

For the local exact null controllability,we can get the same conclusion(especially Theorem 2.2)as in the previous section under much less hypotheses.

Theorem 3.1(Local One-Sided Exact Null Controllability)For any givenδ(0< δ<),letT>0satisfy(2.14).

(A)Suppose that in boundary conditions(1.15)onx=L,we have

Then,for any given initial dataϕwith smallC1[0,L]norm,such that the conditions ofC1compatibility are satisfied at the point(t,x)=(0,L),there exist boundary controlsHr(r=m+1,···,n)with smallC1[0,T]norm and internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the mixed initial-boundary value problem(1.10)and(1.13)–(1.15)admits a uniqueC1solutionu=u(t,x)with smallC1norm on the domainR(T),which satisfies exactly the zero final condition(1.18).

(B)Suppose that in boundary conditions(1.14)onx=0,we have

Then,for any given initial dataϕwith smallC1[0,L]norm,such that the conditions ofC1compatibility are satisfied at the point(t,x)=(0,0),there exist boundary controlsHp(p=1,···,l)with smallC1[0,T]norm and internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the conclusion(A)of Theorem3.1holds.

We only prove the first part of Theorem 3.1.The proof of the second part is similar.To this end,we also construct the characteristic system(2.2),where ci(t,x)(i=1,···,n)are the corresponding internal controls and

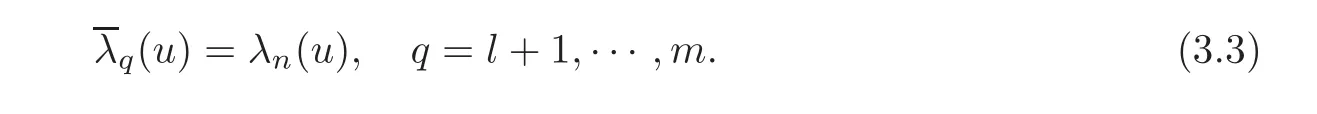
Corresponding to(3.3),we give the following artificial boundary conditions:

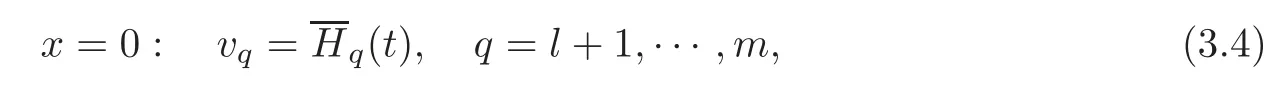
in which(t)(q=l+1,···,m)are C1functions of t.

For the mixed initial-boundary value problem(2.2),(1.13)–(1.15)and(3.4),according to the result on local one-sided exact null controllability in[7],we have the following lemma.

Lemma 3.1Under the hypotheses of Theorem3.1(A),suppose furthermore that(3.3)holds.LetT>0be defined by(2.14).For any given initial dataϕwith smallC1[0,L]norm,such that the conditions ofC1compatibility are satisfied at the point(t,x)=(0,L),there exist boundary controlsandHr(q=l+1,···,m;r=m+1,···,n)with smallC1[0,T]norm and internal controls(t,x)(i=1,···,n)given by(2.5),in which theC1[R(T)]norm ofand(i=1,···,n)is suitably small,such that the mixed initial-boundary value problem(2.2)and(1.13)–(1.15)and(3.4)admits a uniqueC1solutionu=u(t,x)with smallC1norm on the domainR(T),which satisfies exactly the zero final condition(1.18).

By Lemma 3.1,we can prove Theorem 3.1.

In fact,substituting the C1solution u=u(t,x)given by Lemma 3.1 into boundary conditions(1.14),we get the desired boundary controls Hr(r=m+1,···,n)given by(2.7),where υi(i=1,···,n)are defined by(1.12).Noting(1.16),the C1norm of Hr(r=m+1,···,n)is suitably small.On the other hand,substituting u=u(t,x)into the system(1.10),we get the desired internal controls ci(t,x)(i=1,···,n)given by(2.8),which correspond to(1.11)with(2.9).Noting(1.9),the C1[R(T)]norm of ϑ and ki(i=1,···,n)is also small.Thus,we obtain the desired exact controllability.

4 Local Exact Internal Controllability

Under some special but meaningfulassumptions,we may realize the local exact controllability only by internal controls.Suppose that the number of positive eigenvalues is equal to that of negative ones,i.e.,

Suppose furthermore that in a neighborhood of u=0,the boundary conditions(1.14)–(1.15)can be equivalently rewritten as

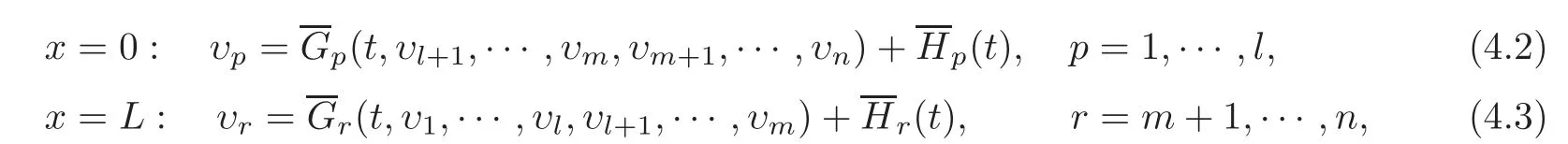
respectively.Without loss of generality,we may assume that

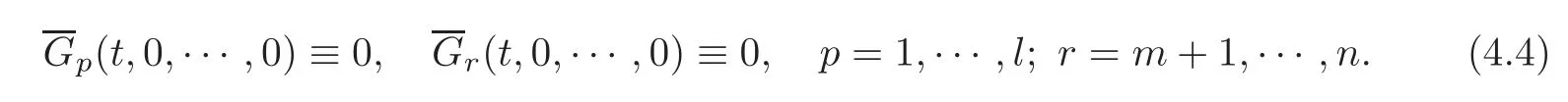
Then

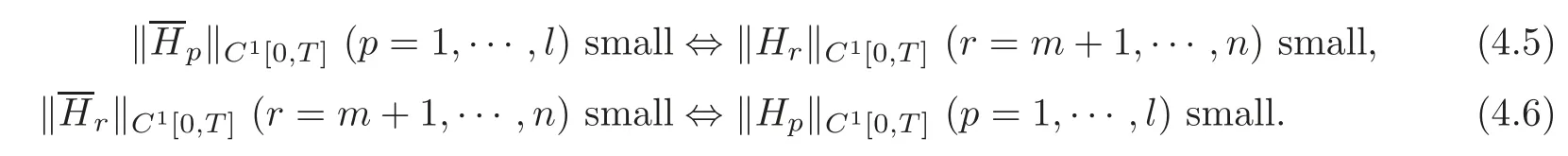
Theorem 4.1(Local Exact Internal Controllability)Under the hypotheses of Theorem2.1,suppose furthermore that(4.1)–(4.4)hold.For any givenδ(0< δ<),ifT>0satisfies(2.14),then for any given initial dataϕand final dataψwith smallC1[0,L]norm,and for any givenHpandHr(p=1,···,l;r=m+1,···,n)with smallC1[0,T]norm,such that the conditions ofC1compatibility are satisfied at the points(t,x)=(0,0),(0,L),(T,0)and(T,L),respectively,there exist internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the conclusion of Theorem2.1holds.

To prove Theorem 4.1,we introduce the following unknown vector function of(t,x):

and a set of(n+m−l)-D row vectors

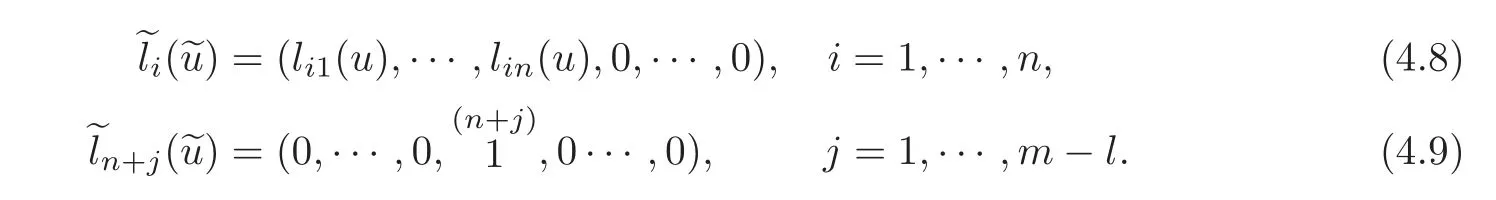
Obviously,is a set of linearly independent vectors.

We construct the following system of characteristic form:

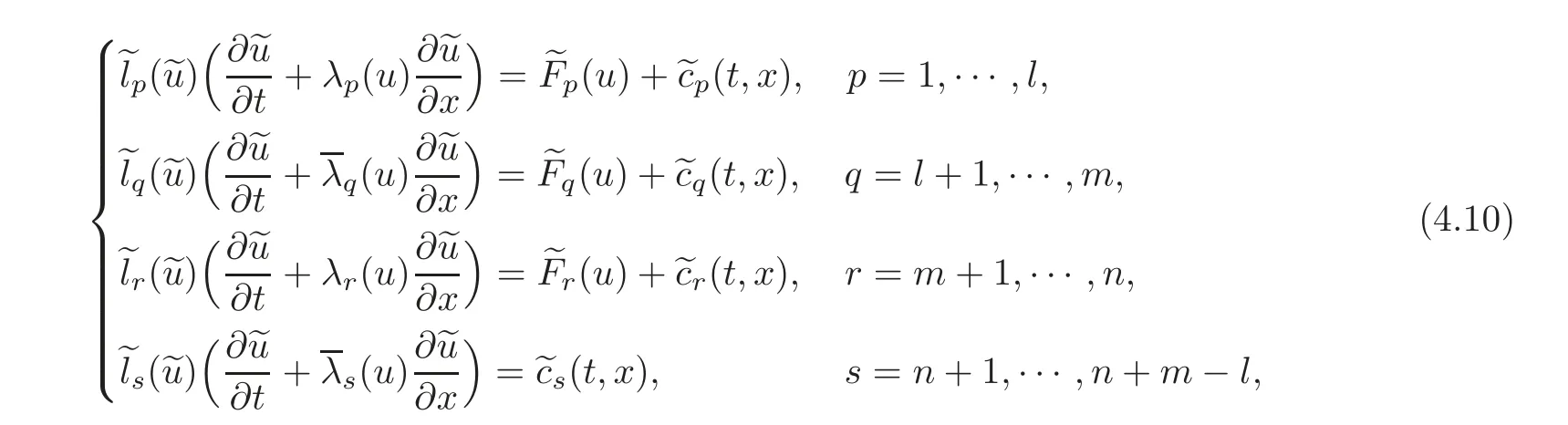
where(t,x)(i=1,···,n+m − l)are the corresponding internal controls and

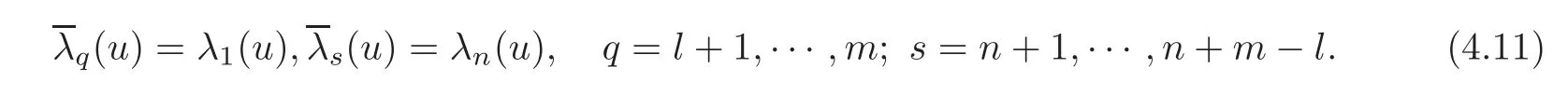
Noting(4.8)–(4.9),the system(4.10)can be simpli fied into

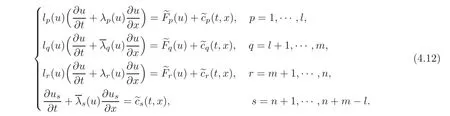
Obviously,(4.10)is a system without zero eigenvalues.Let

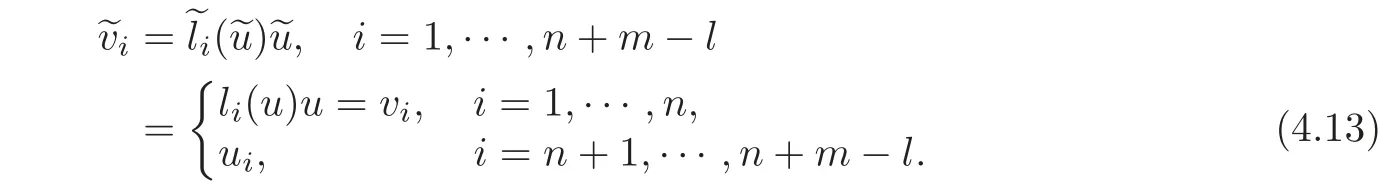
We give the initial condition

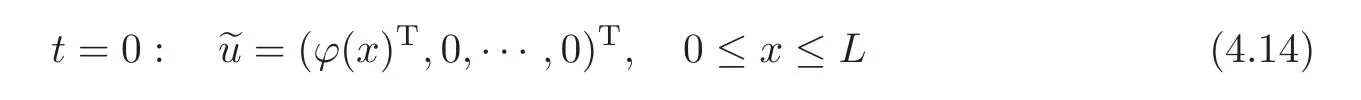
and the final condition

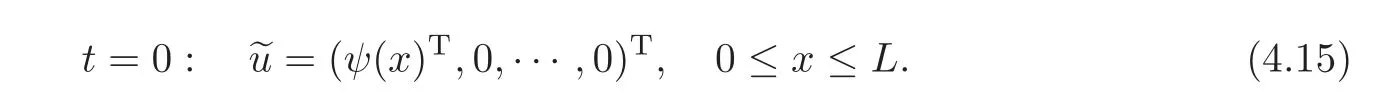
Corresponding to(4.11),we give the following artificial boundary conditions:

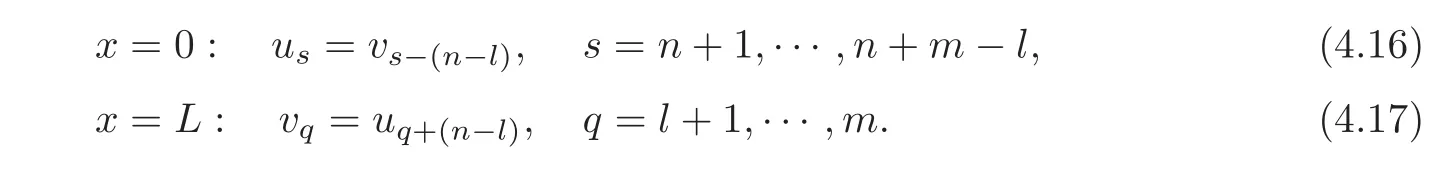
For the mixed initial-boundary value problem(4.10),(4.14),(1.14)–(1.15)and(4.16)–(4.17),according to the result on local exact internal controllability in[7],we have the following lemma.

Lemma 4.1Under the hypotheses of Theorem4.1,suppose furthermore that(4.11)holds.LetT>0be defined by(2.14).For any givenϕandψwith smallC1[0,L]norm,and for any givenHpandHr(p=1,···,l;r=m+1,···,n)with smallC1[0,T]norm,such that the conditions ofC1compatibility are satisfied at the points(t,x)=(0,0),(0,L),(T,0)and(T,L),respectively,there exist internal controls

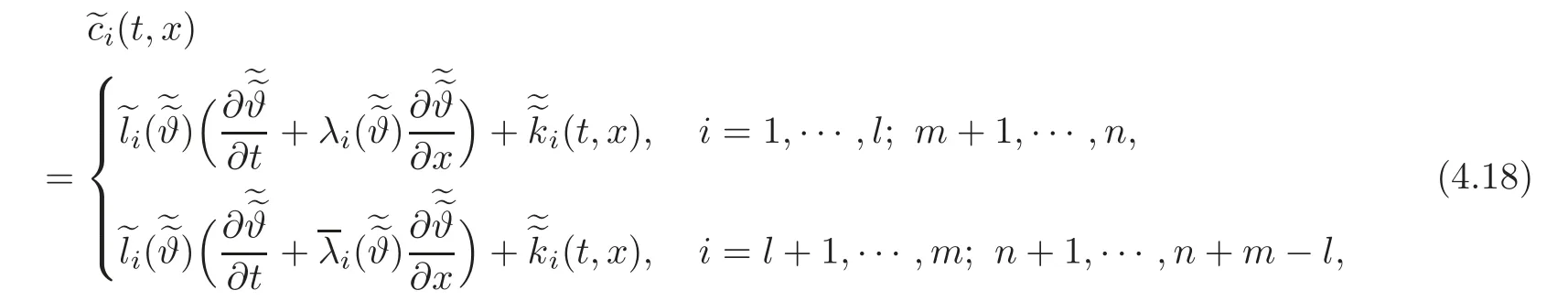
in whichanddepend only on the firstncomponents of,and theC1[R(T)]norm ofand(i=1,···,n+m−l)is suitably small,such that the mixed initial-boundary value problem(4.10),(4.14),(1.14)–(1.15)and(4.16)–(4.17)admits a uniqueC1solution=(t,x)with smallC1norm on the domainR(T),which satisfies exactly the final condition(4.15).

By Lemma 4.1,we can prove Theorem 4.1.

In fact,let u=u(t,x)=(u1,···,un)Tbe the column vector composed of the first n components of the C1solution u=u(t,x)given by Lemma 4.1.Obviously,u=u(t,x)veri fies boundary conditions(1.14)–(1.15),the initial condition(1.13)and the final condition(1.17).Substituting u=u(t,x)into the system(1.10),we get the desired internal controls ci(t,x)(i=1,···,n)given by(2.8),which correspond to(1.11)with(2.9).Noting(1.9),the C1[R(T)]norm of ϑ and ki(i=1,···,n)is also small.Thus,we obtain the desired exact controllability.

If we consider only the exact null controllability and assume that(3.1)–(3.2)hold,then we can still get the local exact internal controllability without assumptions(4.1)–(4.4).

Theorem 4.2(Local Exact Internal Null Controllability)Under the hypotheses of Theorem2.1,suppose furthermore that(3.1)–(3.2)hold.For any givenδ(0< δ<),ifT>0satisfies(2.14),then for any given initial dataϕwith smallC1[0,L]norm,such that the conditions ofC1compatibility are satisfied at the points(t,x)=(0,0)and(0,L),respectively,there exist internal controlsci(t,x)(i=1,···,n)given by(1.11),in which theC1[R(T)]norm ofϑandki(i=1,···,n)is suitably small,such that the conclusion of Theorem4.1holds for the zero final condition(1.18).

The proof of Theorem 4.2 is similar to that of Theorem 4.1.

5 Remarks

Remark 5.1The estimate given by(2.1)and(2.14)on the control time in Theorems 2.1–4.2 is sharp.By(2.1)and(2.14),the larger the value δ,the smaller the control time T.In particular,when δ→,the right-hand sides of(2.1)and(2.14)tend to zero.It shows that by means of internal controls one can realize the local exact controllability almost immediately in principle.

Remark 5.2By[7],for first-orderquasilinear hyperbolic systems without zero eigenvalues,the internal controls are acting only on the rectangle[ε0,T −ε0]×[−δ,+δ],where ε0>0 is suitably small.Thus,by(2.2)and the first n equations in(4.12),in the domains[0,T]×[0,−δ]and[0,T]×[+δ,L],the internal controls in Theorems 2.1–4.2 are added only to those equations corresponding to zero eigenvalues.

Remark 5.3The boundary controls and the internal controls given in Theorems 2.1–4.2 are not unique.

AcknowledgementThe author would like to express her sincere gratitude to Professor Li Tatsien for his effective instruction.

[1]Li,T.T.,Controllability and Observabilty for Quasilinear Hyperbolic Systems,AIMS Series on Applied Mathematics,Vol.3,American Institute of Mathematical Sciences&Higher Education Press,Spring field,Beijing,2010.

[2]Li,T.T.and Rao,B.P.,Local exact boundary controllability for a class of quasilinear hyperbolic systems,Chin.Ann.Math.,23B(2),2002,209–218.

[3]Li,T.T.and Rao,B.P.,Exact boundary controllability for quasilinear hyperbolic systems,SIAM J.Control Optim.,41,2003,1748–1755.

[4]Li,T.T.and Rao,B.P.,Strong(Weak)exact controllability and strong(weak)exact observability for quasilinear hyperbolic systems,Chin.Ann.Math.,31B(5),2010,723–742.

[5]Li,T.T.and Yu,L.X.,Exact controllability for first order quasilinear hyperbolic systems with zero eigenvalues,Chin.Ann.Math.,24B(4),2003,415–422.

[6]Zhang,Q.,Exact boundary controllability with less controls acting on two ends for quasilinear hyperbolic systems,Appl.Math.J.Chinese Univ.Ser.A,24(1),2009,65–74.

[7]Zhuang,K.L.,Li,T.T.and Rao,B.P.,Exact controllability for first order quasilinear hyperbolic systems with internal controls,Discrete Contin.Dyn.Syst.,36(2),2016,1105–1124.