Positivity of Fock Toeplitz Operators via the Berezin Transform∗

Xianfeng ZHAO

1 Introduction

Let dμ be the Gaussian measure on the complex plane C.It is well-known that,in terms of the standard area measure dA(z)=dxdy=drdθ on C,we have

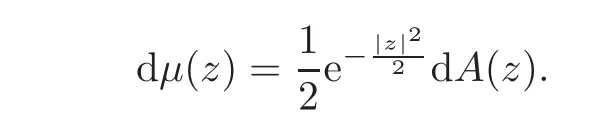
Recall that the Fock space F2is defined to be the subspace

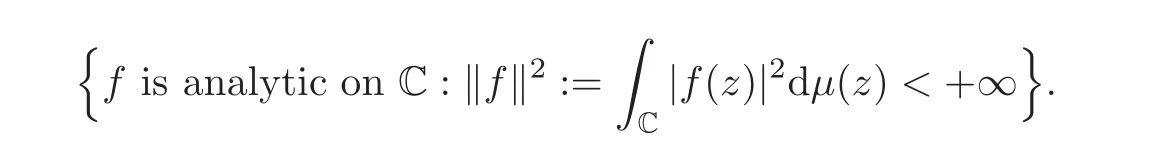
It is easy to check that the functions zn(n≥0)are orthogonal in F2and their linear span is dense in F2.Using polar coordinates we get that.Thus

2.1 BMI对肝癌术后OS的影响 Kaplan-Meier分析显示，在388例HCC患者中，消瘦组、体质量正常组与超重肥胖组的中位生存时间分别为21、66、81个月；在208例ICC患者中，消瘦组、体质量正常组与超重肥胖组的中位生存时间分别为8.3、18、26个月。

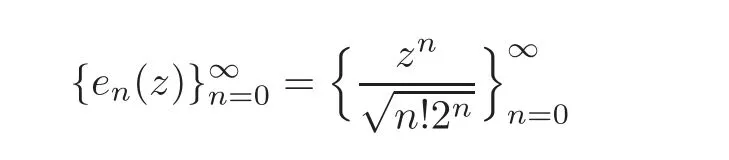
forms an orthonormal basis of the Fock space F2.

军队行政权力清单制度，是对行政权力进行标准规范、制约和监督，建立与运行涉及关系十分复杂。首先，将各级机关及其部门的行政权力详细罗列，把各机关部门之间的权力界面划分清楚，实现行政权力在军队内部合理优化配置。其次，查找本单位本部门行政权力不够明晰、存在交叉的地方，减少非军事权力事项，调整不合理权力事项，科学配置部门行政权力，优化权力运行流程。再次，严格按照各级各部门的行政权力清单和权力运行流程图来行使权力，使权力运行的各个环节符合法规要求，确保权力运行的全过程处于正常状态。最后，将制定的行政权力清单及权力运行流程图公布出来，接受广大官兵的监督，使权力置于公开、透明的阳光之下。

Given ϕ in L∞(C),the Fock Toeplitz operator with symbol ϕ is defined by

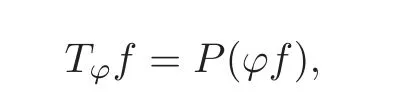
which shows that

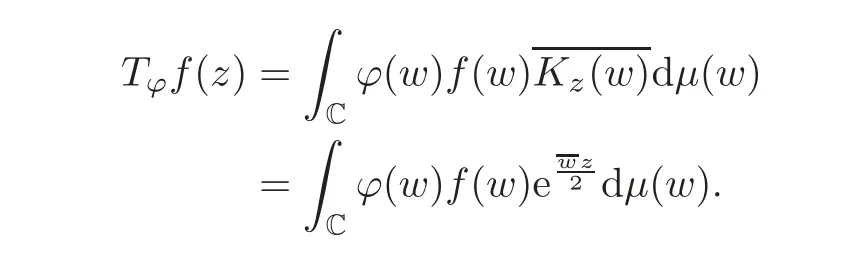
For more information on the topics of the Fock space and Fock Toeplitz operators,we refer to[2–3,9].

近年来，常州市委、市政府高度重视人才工作，深入实施创新驱动战略和人才强市战略，不断深化“龙城英才计划”改革创新，通过优化人才政策体系，完善人才创新创业平台，营造人才发展良好生态环境，积极助推人才队伍建设，尤其是科技人才梯队建设。目前，常州市科技人才队伍建设已取得了一定成效，初步形成了一只高水平、多层次的科技人才队伍，为实现产业转型升级、扎根常州“幸福树”、建设“强富高美”新常州提供了坚实的智力支持。

As usual,let kzdenote the normalized reproducing kernel for F2.That is,

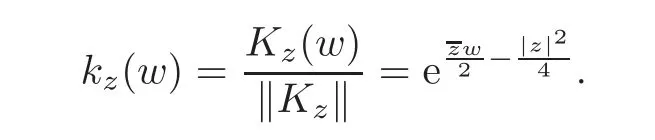
For a bounded operator A on the Fock space F2,the Berezin transform of A is the function A on the complex plane defined by

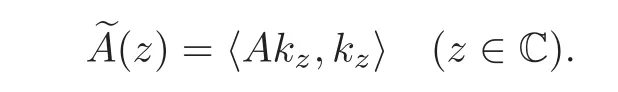
For ϕ ∈L∞(C),is called the Berezin transform of ϕ given by

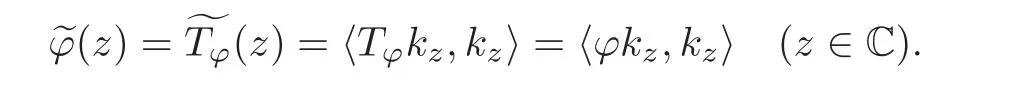
The Berezin transform is a very usefultool in studying Toeplitz operators on the Bergman space and the Fock space.For instance,the compactness,boundedness,positivity,invertibility and Fredholmness of the Toeplitz operators are partially or completely characterized by their Berezin transforms(please see[1,4–5,7–8]).

Recently,the author and Zheng[6]studied the positive Toeplitz operators on the Bergman space via their Berezin transforms.They showed that the positivity of a Toeplitz operator on the Bergman space is not completely determined by the positivity of the Berezin transform of its symbol.Indeed,they constructed a quadratic polynomial of|z|on the unit disk and showed that even if the minimal value of the Berezin transform of the polynomial is positive,the Toeplitz operator with the function as the symbol may not be positive.

从近些年的案例来看，在互联网领域，各商家应该遵守广电总局颁布的法律法规。2017年6月份，国家对新浪、凤凰网等下达了明确的规定，在这些网络新闻平台中如不符合相关的管理条例，就要停顿进行整改。2018年1月份，国家约谈了花椒直播软件的负责人，责令其对平台中不法行为进行全面整改。同年4月份，国家广播电视总局约谈了受社会舆论关注的“快手”“今日头条”两家网站的主要负责人，并责令“今日头条”网站关闭“内涵段子”板块，并且永久不能开启。

Motivated by this result,we try to study the positivity of the Toeplitz operators on the Fock space in the present paper.Observe that from the definition of the Berezin transform we see that the function ϕ is nonnegative on C provided that Tϕ≥0,and Tϕ≥0 if the function ϕ(z)≥0 for all z∈C.Thus,it is natural to ask the following question.

Question 1.1Is the positivity of a Fock Toeplitz operator completely determined by the positivity of the Berezin transform of its symbol?If not,then how to construct the “simplest”function ϕ which satisfies that ϕ is positive on the complex plane but the Toeplitz operator Tϕis not positive?

As we mentioned above,one can find an example from the set

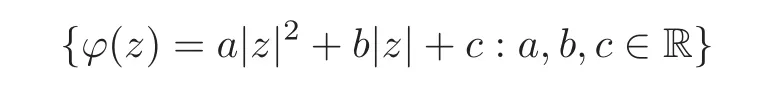
such that Tϕis not positive on the Bergman space but ϕ is strictly positive on the unit disk.So,it is natural to try to use the radial functions(i.e.,ϕ(z)= ϕ(|z|)for all z∈ C)of the formto construct a suitable example and give a negative answer to the above question.However,these simple radial functions are not bounded on the complex plane C.Our main idea in this paper is to simplify our calculations and estimations by the bounded radial functions e−λ|z|2(λ >0).More precisely,we will consider the bounded radial functions of the following form:

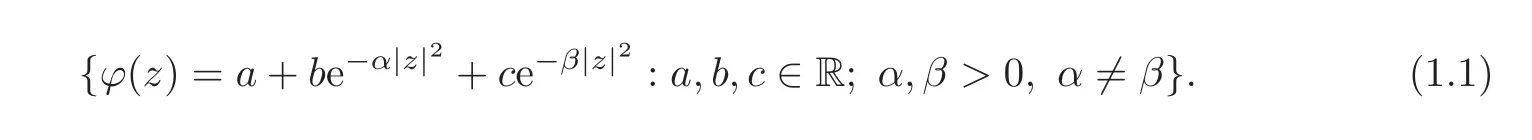
Question 1.2Is there a function ϕ in(1.1)such thatbut Tϕis not positive on F2for all 2α=β>0?

Based on the answer to Question 1.1,we will give a negative answer to Question 1.2 by taking 2α= β=and showing that Tϕis positive if and only if its Berezin transform is a nonnegative function in this case.That is,for this type of α and β,there do not exist a,b,c such that ϕ is positive but Tϕis not.The proofs will be given in the last section.

2 Preliminaries

It is difficult to study the positivity of the Toeplitz operators on function spaces in the general case even if the symbols are continuous functions.However,if ϕ is a radial function on C,we can find the relationship between the positivity of Tϕand the Berezin transform ϕ by its matrix,since the matrix representation of this type of Toeplitz operator is a diagonal matrix under the orthonormal basis.

Lemma 2.1Suppose thatϕis a bounded radial function onC.Then the matrix represen-tation of the Toeplitz operatorTϕunder the basisis

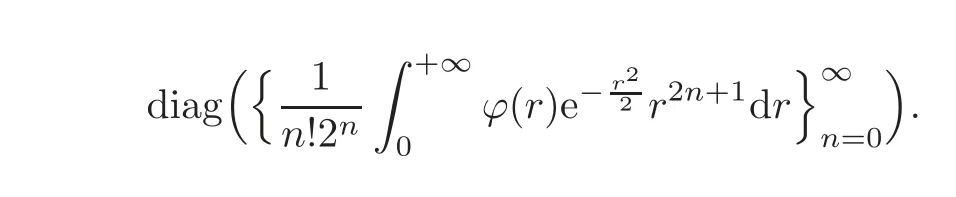
In particular,if

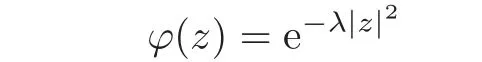
withλ >0,then the matrix representation ofTϕis given by

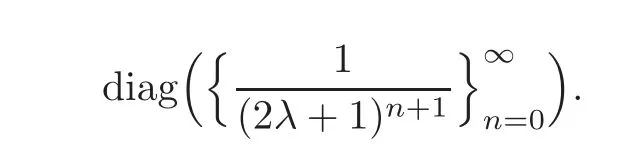
ProofFor each n≥0,we have

If ϕ(z)=e−λ|z|2(λ >0)and n≥0,then we have

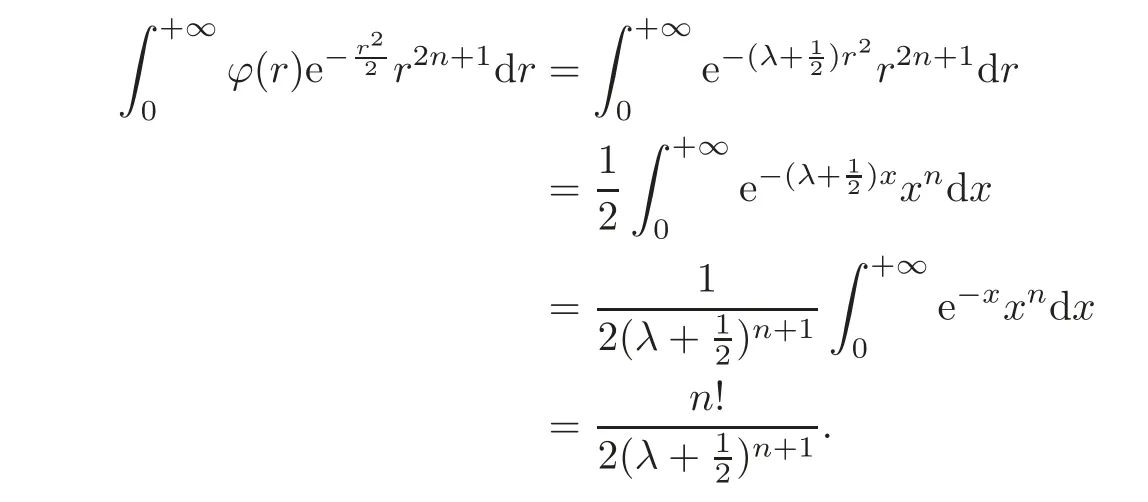
Thus,

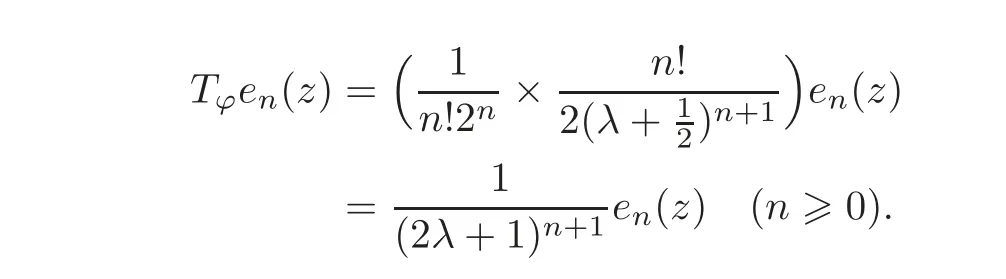
This completes the proof of Lemma 2.1.

Note that for the Bergman space case,the Berezin transforms of the functions|z|l(l≥0)are so complicated even if these functions are very simple(see[6,Lemma 3.3]).However,the Berezin transform of the function e−λ|z|2(λ >0)on C has a good expression,that is the following lemma,which is very usefulfor proving our main results.

Lemma 2.2Suppose thatϕis a bounded radial function onC.Then the Berezin transform ofϕis given by

for some N＞2.However,this is impossible.The contradiction shows that

In particular,ifϕ(z)=e−λ|z|2withλ >0,then

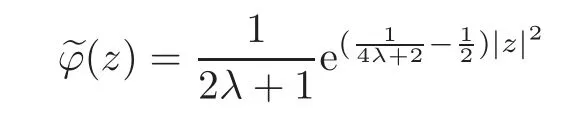
for allz∈C.

For the special case,we have the following simple calculations:

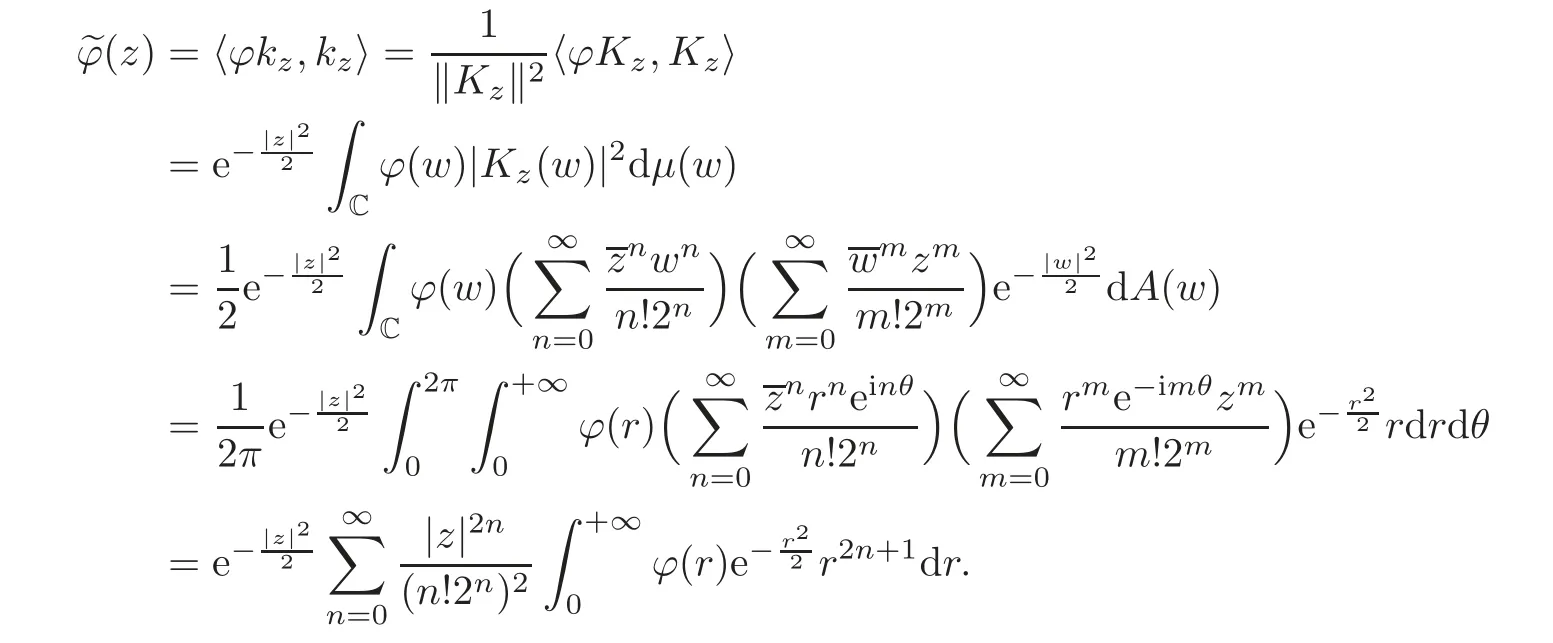
ProofBy the definition of the Berezin transform,we have

来旅游的男同学几年不见已秃顶成“地中海”模式，他摸着自己的“地中海”头顶自嘲道，自打娶了个小八岁的萌妹子，又当夫又当父的，因为操劳过度，导致提前步入“黄金老年组”。我们几个哄堂大笑。傲娇的萌妹子当场撒娇无极限，拿起手机向父母告状，乐极生悲的“地中海”同学赶紧接受手机里丈母娘的严厉批评，当着大家的面冲萌妹子又是鞠躬又是讨饶，我直觉身边的乔振宇浑身战栗了几下。

where the last“=”comes from the proof of Lemma 2.1.Therefore,

This gives that,so(3)⇔ (2).This completes the proof.

as desired.

Before studying the answer to Question 1.1,we first consider the function ϕ in(1.1)with c=0.Combining the above two lemmas,we get the following result.

Proposition 2.1Letϕ(z)=a − e−λ|z|2,wherea ∈ Randλ >0.Then the following conditions are equivalent:

(1)The Fock Toeplitz operatorTϕis positive;

(2)a

我和阿花去了中汕厂，直闯总经理室。中汕厂的老板江锋挺友善，非常客气地接待了我们。本以为江老板也像林老板那么老气横秋老奸巨滑呢，没想到江老板才三十来岁，仪表堂堂，高大挺拔，谈吐不俗，侃侃道来，讲商场上的道理，讲做人与做事的道理，哲理性很强。江老板说得冠冕堂皇，中汕厂中止和你们合作，不是慑服于谁，而是出于对合作单位的尊重，我们可以跟你们合作，给你们订单，但前提是，你们必须修复和大发厂的关系，否则我们只能求大舍小。

(3)The Berezin transformfor allz∈C.

图2中，短期修正在绿色区域为正常，也就是“6”代表的区域，一般来说长期和短期修正的叠加值在±15%以内。如果处于“5”代表的黄色区域，则有可能是发动机存在故障，如发动机转速不稳。从数值看，长短期修正叠加在+15%～+35%之间和-15%～-35% 之间，或者单独的短期修正在+15%～+20%之间和-15%～-20%之间，在这两个区域内发动机的尾气可以被修正补偿到合格范围内。此时，如果进行尾气检测，一般会合格，发动机抖动的原因只能通过数据分析才能查明。

ProofBy Lemma 2.1,we get that the matrix representation of Tϕis

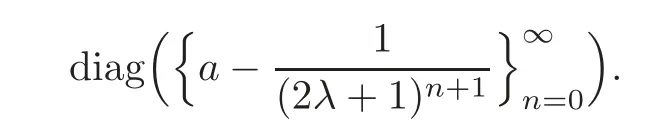
Thus,Tϕis positive if and only iffor all n≥0,which gives thatThis proves(1)⇔(2).Now Lemma 2.2 implies

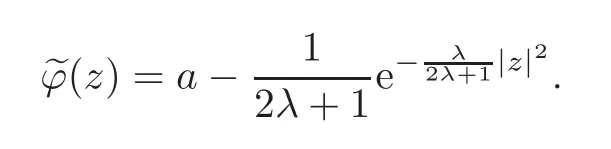
So we obtain thatis nonnegative on C if and only if

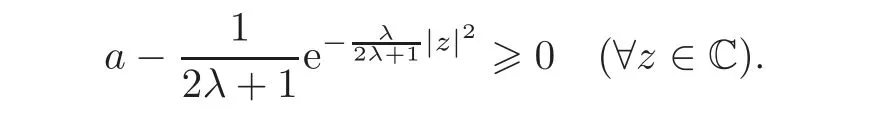
中心数据显示，目前中心日间手术床位28张，单个手术间单日日间手术最高可达22台。目前，全院共开设七大专科、130多种儿科日间手术，80余种妇科日间手术，这些手术使患者等待时间缩短了50%以上，住院时间由原来2～3天缩短为4～6小时。

Remarks 2.1The above proposition tells us that there exists a function ϕ ∈ L∞(C)such that the Fock Toeplitz operatobut ϕ is not a nonnegative function on C.To see this,we only need to takewith λ >0 in Proposition 2.1.Furthermore,this result also implies that to give a negative answer to Question 1.1,we only need to consider the case ofandin(1.1).

3 A Negative Answer to Question 1.1

In this section,we construct a function ϕ such that the Berezin transform of ϕ is positive on the complex plane but the corresponding Fock Toeplitz operator is not positive.To do so,we first consider the case 2α=β=1.Without loss of generality,we may assume c=1.Then we have the following theorem.

Theorem 3.1Suppose that,wherea,b∈ R.Then

艾瑞克眉毛处戴的金属环反射出刺眼的光。我似乎明白了他们的关系，艾瑞克把老四视为他职位的潜在威胁。我想起父亲说过：奢望权力并达到目的的人，整天提心吊胆，生活在对失去权力的恐惧中，这就是为什么权力应赋予不奢望权力的人。

(1)ifb−orb≤0,thenTϕis positive if and only ifis a nonnegative function on the complex plane;

(2)for eachb∈(−,−],there exists a real numberasuch thatfor allz∈C,butTϕis not a positive Toeplitz operator.

ProofUse Lemmas 2.1–2.2 and let λ =,1,respectively.Then we obtain that the matrix representation of Tϕis given by

and the Berezin transform of ϕ is

由表2可见，孵育45 min时，在NADPH启动的Ⅰ相孵育体系和UDPGA启动的Ⅱ相孵育体系中，ZG02的剩余百分比分别为（73.33±1.53）%、（50.63±3.42）%，t1/2分别为67.28、30.26 min，表明其在单相孵育体系中的代谢稳定性中等，且在Ⅱ相中的代谢稳定性较Ⅰ相差；在NADPH和UDPGA联合启动的两相孵育体系中，ZG02的剩余百分比为（45.81±2.56）%，t1/2为25.57 min，提示其在两相孵育体系中的代谢稳定性差。

ProofBy Lemma 2.1,we see that the matrix representation of Tϕis

for all,andif and only if

for all z∈C.Therefore,is equivalent to

Letting∈[0,1],thenis equivalent to

First,we prove part(1)of the above theorem.Now we are going to determine the minimal value of the functionand the minimal term of the sequenceTo do this,we consider the following two cases.

Case ISuppose that b≥0.It is easy to see that f(t)is increasing on[0,1]andis decreasing for n＞1.So we have

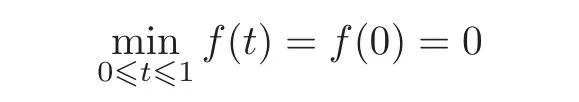
and

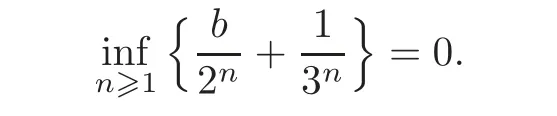
Case IISupposeA simple calculation gives that f(t)is decreasing ifand f(t)is increasing ifNote that,so

陕西省中小河流分布广、战线长、数量多，不仅直接关系到广大人民群众的生命财产安全，而且关系到全面建设小康，构建社会主义和谐社会、建设社会主义新农村等重大战略目标的顺利实现。

精确液体管理组1周内停用呼吸机的比率明显高于对照组，分析主要是因为通过PiCCO监测能更合理制定液体治疗方案，及时纠正休克和心衰，缩短液体正平衡时间，减轻因组织器官水肿、微循环障碍等继发的MODS[16]，实现早脱机的目标。

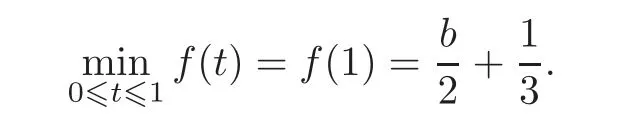
To find the minimal term of the sequence,observe thatand we claim thatis the minimal term.Indeed,if there exists some N>1 such that

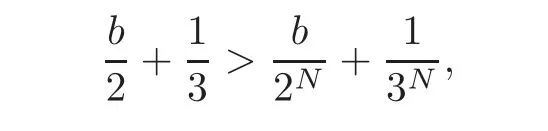
then we obtain

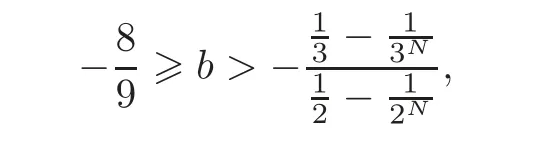
where P:L2(C,dμ)→ F2is the orthogonal projection.Using the reproducing kernel Kz(w)=,we express the Toeplitz operator as an integral operator:

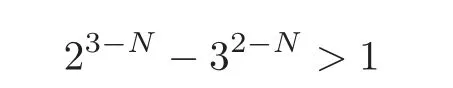
有机农业（Organic Agriculture）是遵照一定的有机农业生产标准，在生产中不采用基因工程获得的生物及其产物，不使用化学合成的农药、化肥、生长调节剂、饲料添加剂等物质，遵循自然规律和生态学原理，协调种植业和养殖业的平衡，采用一系列可持续发展的农业技术以维持持续稳定的农业生产体系的一种农业生产方式。

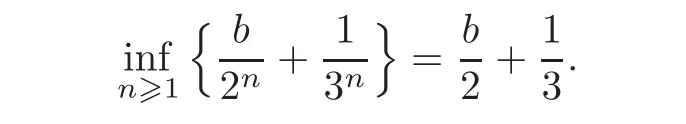
Combining the above two cases gives the conclusion in part(1).

For the second part,we turn to consider b ∈ (−,−].First,observe that Tϕis not positive if and only if

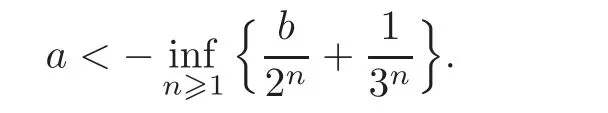
To finish the proof,it suffices to show that for each b ∈ (−,−],there exists a real constant a such that

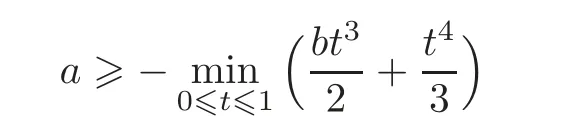
and Tϕis not positive.As shown above,we need the following inequality:

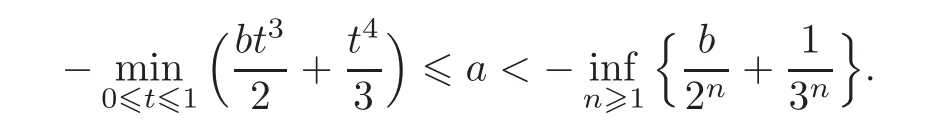
Indeed,we will show that

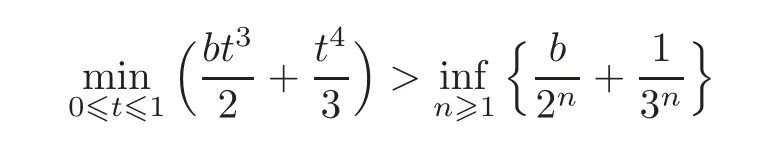
for each b∈ (−,−].To do this,we first find the minimal value of f(t).Note thatifUsing the monotonicity of the function f(see the argument in Case II),we get that

On the other hand,we have the following inequality:

for eachIndeed,if we consider the function

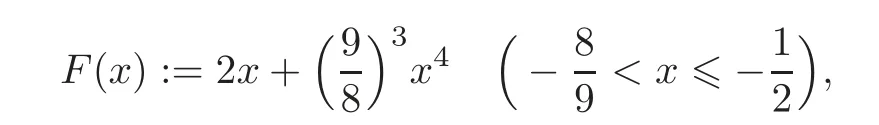
then the first inequality follows immediately from the mean value theorem.This finishes the proof of Theorem 3.1.

One may ask that if we remove the condition 2α = β,can we easily construct an example from(1.1)to give a negative answer to Question 1.1?Actually,we will show that the answer is yes by the following corollary,which can be proved by the same method as the one in the above theorem,so we omit its proof here.

Corollary 3.1Letwherea,b∈ R.Then for eachthere exists a real numberasuch thatfor allz∈C,butTϕis not a positive Toeplitz operator onF2.

4 A Negative Answer to Question 1.2

In Section 3,we study the radial function ϕ(z)=a+be−α|z|2+ce−β|z|2(a,b,c∈ R,α,β >0)and choose real numbers a,b and c such thatis nonnegative on C and Tϕis not positive under the assumption 2α= β=1.In the final section,we will show that this is not true for all 2α=β>0.More precisely,we have the following theorem,which gives a negative answer to Question 1.2 with the condition 2α=β=

Theorem 4.1Suppose thatwherea,b∈ R.ThenTϕis positiveif and only ifϕ(z)is a nonnegative function onC.

These imply thatif and only if

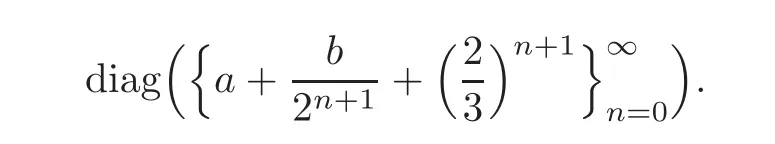
So,Tϕ?0 if and only if

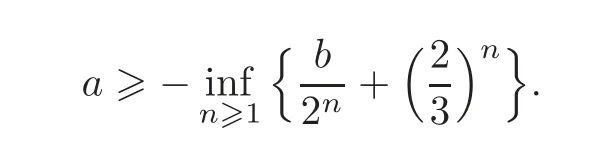
On the other hand,using Lemma 2.2 we obtain thatfor all z∈C if and only if for all z∈C.

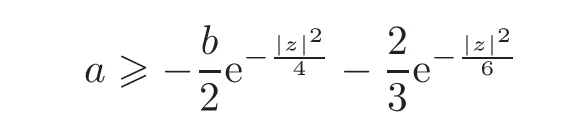
Letting[0,1]andwe see that the above condition on the positivity of ϕ is equivalent to

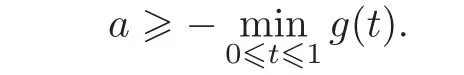
Using the same idea as the one in the proof of Theorem 3.1,we divide the proof into the following four cases.

Case IWe first consider the case.It is easy to see that

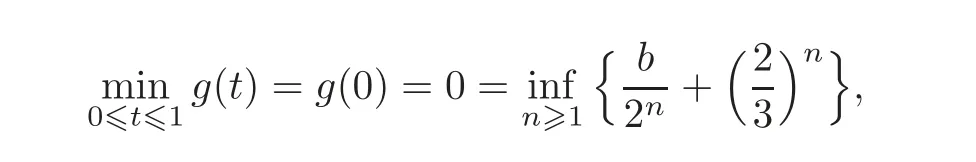
which shows that Tϕis positive if and only if ϕ is a nonnegative function on C.

Case IISuppose thatIt is easy to check that g(t)is increasing ifand decreasing ifObserve thatso we have

On the other hand,we have

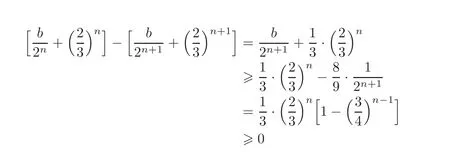
for allprovided thatThis implies that the sequenceis decreasing,so the minimal term isas desired.

Case IIIIn this case,we considerNote thatand

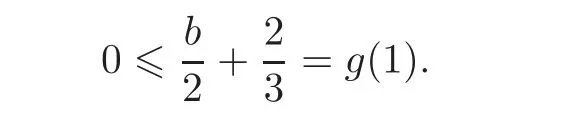
It follows from the argument in Case II that

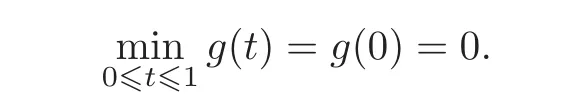
Also,it is easy to see thatfor allThis gives that

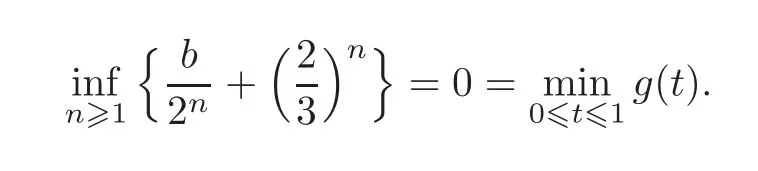
Case IVFinally,we deal with the caseThenandIt follows that

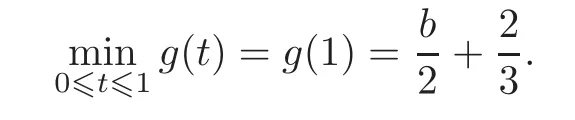
Now using the same techniques as the one in Case II of Theorem 3.1,we see that the minimal term of the above sequence is the first term.We conclude that

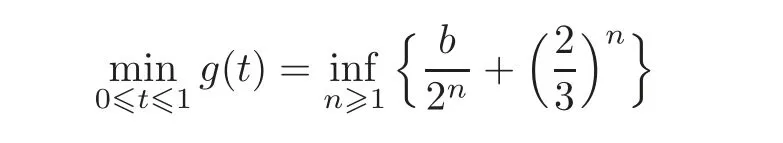
for all b∈R.This completes the whole proof.

AcknowledgementThe author thanks the referees for their many suggestions.

[1]Axler,S.and Zheng,D.C.,Compact operators via the Berezin transform,Indiana Univ.Math.J.,47(2),1998,387–400.

[2]Isralowitz,J.and Zhu,K.H.,Toeplitz operators on the Fock space,Integral Equations and Operator Theory,66(4),2010,593–611.

[3]Stroetho ff,K.,Hankel and Toeplitz operators on the Fock space,The Michigan Mathematical Journal,39(1),1992,3–16.

[4]Stroetho ff,K.,The Berezin Transform and Operators on Spaces of Analytic Functions,Banach Center Publications,38,Polish Academy of Sciences,Warsaw,1997,361–380.

[5]Stroetho ff,K.and Zheng,D.C.,Products of Hankel and Toeplitz operators on the Bergman space,Journal of Functional Analysis,169(1),1999,289–313.

[6]Zhao,X.F.and Zheng,D.C.,Positivity of Toeplitz operators via Berezin transform,Journal of Mathematical Analysis and Applications,416(2),2014,881–900.

[7]Zhao,X.F.and Zheng,D.C.,Invertibility of Toeplitz operators via Berezin transforms,Journal of Operator Theory,to appear.

[8]Zhu,K.H.,Operator Theory in Function Spaces,2nd edition,Mathematical Surveys and Monographs,138,American Mathematical Society,Providence,2007.

[9]Zhu,K.H.,Analysis on Fock Spaces,Graduate Texts in Mathematics,263,Springer-Verlag,New York,2012.