《完全平方公式》教学设计

♡牡丹江市田家炳实验中学　张慧英



《完全平方公式》教学设计

♡牡丹江市田家炳实验中学张慧英

一、学情分析：知识链接:1.同类项的定义；2.合并同类项法则的正确应用；3.多项式乘以多项式法则；4.平方差公式的内容。

二、教学目标：学生通过求面积的几何题了解完全平方公式的几何意义，经历探索完全平方公式（a+b）2= a2+2ab+b2的过程,并能运用公式进行简单的计算.通过自主探究，合作交流，让学生更好地理解公式内容，并为公式的应用打下坚实的基础.

三、教学重点：完全平方公式的准确应用，与平方差公式的区别.

四、教学难点：掌握公式中字母表达式的意义；灵活运用公式进行计算.

五、教学流程：问题情景—探究交流—得出结论—强化训练.

六、教学媒体：多媒体课件.

七、教学和活动过程:

（一）课前复习，巩固旧知（略）

（二）数形结合，分析问题

1.情境导入

去年，一位农民在一次“科技下乡活动中得到启示，将一块边长为a米的正方形农田改成试验田，一年来，收益很大，于是他想把原来的试验田边长增加b米，形成四块试验田，种植不同的新品种.

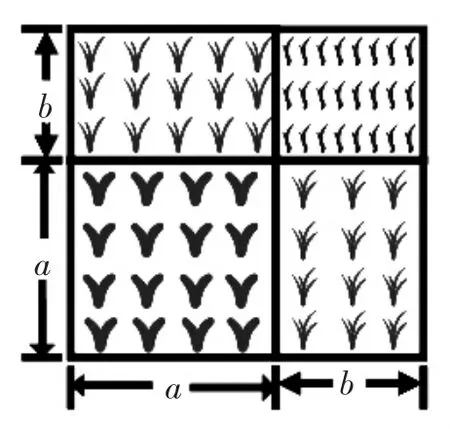
2.思考探索，引入新知

师：你能用不同的方法表示新试验田的面积吗？

生：直接求法：（a+b）2；间接求法：a2+2ab+b2.

设计意图：让学生感受到完全平方公式的几何意义.

由于所求面积相等，因此得出两数和的完全平方公式：（a+b）2=a2+2ab+b2；

语言叙述：两数和的平方，等于它们平方的和，加上它们乘积的2倍。

思考：小明写出了如下（a-b）2=[a+（-b）]2的算式:他是怎么想的?（由猜想引出另一种完全平方公式.）

生：有理数减法的法则——减去一个数等于加上这个数的相反数。

两数差的完全平方公式：（a-b）2=a2- 2ab+b2.

语言叙述：两数差的平方，等于它们平方的和减去它们乘积的2倍.

3.总结归纳

完全平方公式:（a+b）2=a2+2ab+b2；（a-b）2=a2- 2ab+b2.

（注：公式中的字母a、b可以表示数、单项式和多项式.）

两数和（或差）的平方,等于它们的平方和,加（或减）它们乘积的2倍.

为了让学生对所学知识熟练掌握，教师根据自己的理解，编制了一段合辙押韵的顺口溜，学生既感到新奇，又朗朗上口，激发了学生的兴趣，提高了学习效率.

记忆口诀：首平方、尾平方，积的2倍放中央，中间符号同前方.

（三）例题讲解

练习巩固，应用新知：

1.下列各式的计算错误在哪里？应该怎样改正？

（1）（a+b）2=a2+b2；（2）（a-b）2=a2- b2；（3）（a+b）2=a2+ab+ b2；（4）（a-b）2=a2+2ab+b2.

2.运用完全平方公式计算：（1）（x+6）2；（2）（y- 5）2；（3）（- 2x+5）2；（4）（-a-2b）2.

例2：运用完全平方公式计算：（1）1012；（2）992（利用公式可以简便运算）

练习巩固，应用新知：（1）1982；（2）60.22.

（四）拓展提升

1. x+y=4，则x2+2xy+y2的值是（）.

A.8 B.16 C.2 D.4

2.（a-b）2+M=a2+2ab+b2，则M的值为（）.

A. ab B. 0 C. 2ab D. 4ab

3.若使x2- 6x+m成为形如（x-a）2的完全平方形式，则m，a的值（）.

A. m=9，a=9 B. m=9，a=3

C. m=3，a=3 D. m=- 3，a=- 2

4.已知a+b=5，ab=6，求a2+3ab+b2的值.若求a2+ab+b2的值呢？

本环节采用竞技模式，每组选出做题最快的同学当“题长”，由他给本组其他同学进行试题的批改，对速度快的个人和小组分别进行奖励，在这一环节中，学生解题热情高涨，课堂气氛活跃.测试后由学生进行部分题目的讲解，对于本节课表现积极的学生给予表扬，鼓励该学生的同时，促进其他学生一起进步.

（五）课堂小结

问：通过本节课的学习，你有什么收获和感悟？

（六）作业

教材第112页第2题.

编辑/王一鸣

E- mail:51213148@qq.com