基于kNN的聚类算法研究
2016-05-18俞青云安徽大学计算机科学与技术学院安徽合肥230601
郑 诚,俞青云(安徽大学 计算机科学与技术学院,安徽 合肥 230601)
基于kNN的聚类算法研究
郑诚,俞青云
(安徽大学计算机科学与技术学院,安徽合肥230601)
摘要:聚类分析在数据挖掘领域中占有重要地位,到目前为止学者们提出了许多的聚类算法.本文提出了一种基于kNN的聚类算法k-NearestNeighborCluster(kNNC).该算法首先找到每个数据点的k个邻居点,然后设置匹配点数n,通过使用每个点的邻居点进行匹配进而达到聚类效果.本文通过三个实验去验证该算法,并且与k-means算法进行比较.实验结果表明,该算法具有稳定的正确率,而其最大的优点是不需要预先设定聚类簇数,它可以大致的找到聚类的簇数.
关键词:kNN算法;k-means算法;聚类分析;微博文本聚类
1 引言
在数据挖掘中,有两个重要的研究方向,一类是聚类算法的研究,还有一类是分类算法的研究.对于分类就是将贴过标签的对象按标签进行分类,而聚类则是指事先没有“标签”而通过某种成团分析找出事物之间存在聚集性原因的过程.
聚类分析又称为群分析,它是研究(样品或指标)分类问题的一种统计分析方法.当前,聚类(Cluster)分析的算法可以分为划分为以下几个大类:
(1)划分法(Partitioning Methods).它的代表算法为k-means算法[1],k-means算法通过随机的选取k个中心点,然后计算每个点到k个中心点的距离,进而达到聚类的效果.它的缺点是需要事先输入聚类簇数k,并且聚类的好坏与中心点的选取密切相关.
(2)层次法(Hierarchical Methods).层次聚类算法又分为层次凝聚和层次分裂,层次凝聚的代表算法为AGNES算法[2],该算法首先将每个对象看成一个类,然后通过合并直到达到要求的簇类数.而层次分裂的代表算法为DIANA算法[3],该算法首先将所有对象看成是一个簇类,然后通过分裂直到达到要求的簇类数.然而他们都需要事先输入簇类数.
(3)基于密度的方法(density-based methods).它的代表算法为DBSCAN算法[4],该算法将具有足够密度的区域划分为簇.然而当对象空间分布的不均匀是,它的聚类效果会很差.
(4)基于网格的方法(grid-based methods).它的代表算法是CLIQUE算法[5],该算法把每个维度划分为不重叠的空间,然后把数据分布在这些区间中划分成单元,然后通过设置的密度阈值识别稠密单元,从而达到聚类效果.然而该算法的效率和聚类质量不高.
(5)基于模型的方法(Model-Based Methods).它的代表算法为SOM算法[6],该算法通过将数据(n维)输出到平面(2维)的降维映射,其映射具有拓扑特征保持性质,使用竞争式学习网络实现聚类.但是该算法对数据的处理时间较长,所以不适合大量数据集.
本文提出了一种基于kNN的聚类算法.通过实验我们计算了实验的准确率(Precision)、召回率(Recall)以及F值(F-Measure),并且与k-means进行比较,表明该算法可以大致的找到聚类簇数.
2 相关工作
K最近邻(kNN,k-NearestNeighbor)算法是属于数据挖掘的分类算法之一,kNN算法的核心思想是计算出每个待分类对象的k个邻近对象,如果该带分类对象的k个邻近对象大部分属于一个类,那么该对象就属于那个类.近年来,学者们对kNN算法的研究层出不穷,kNN也被运用到不少聚类中. 2007年翁芳菲等人提出了一种基于KNN的融合聚类算法(KNNCE)[7],该算法首先对数据集运行N 次KNN算法构造similarity矩阵,然后对该矩阵使用single-link算法确定最终的聚类划分,该算法能够自动确定最佳聚类数.2013年廖礼等人提出了一种KNN-Potential-based算法[8],该算法首相对数据集使用KNN算法得到初始的密度图,然后在对初始的密度用Potential-based算法进行调整,最终确定聚类划分.2015年牛秦洲等人提出了一种基于MCL与kNN的混合聚类算法[9],该算法首先对数据集使用MCL算法进行聚类,然后对聚类结果中的小聚类簇使用KNN分类算法进行再分类,以提高聚类质量.2015年仰孝富等人提出了一种CF树结合kNN图划分的文本聚类算法[10],该算法首先使用KNN算法得到数据集初始的最小簇集合,然后对这些最小簇集合使用BIRCH聚类过程进行聚类.
对于kNN的研究基本上是结合其他算法进行的,而本文提出了一种不依赖于其他算法的kNN聚类算法.
3 k-NearestNeighborCluster(kNNC)
3.1基本定义
定义1待聚类集合S:S={X1,X2,…,Xn},其中Xi集合S的第i个对象,n为对象的个数.
定义2对象Xi={ai1,ai2,…,aij,…,aim},其中aij为对象Xi的第j个属性,m为每个对象属性的个数.
定义3对象之间的距离公式:D(Xi,Xb)=
定义4第i个对象的k个最邻近对象集合:
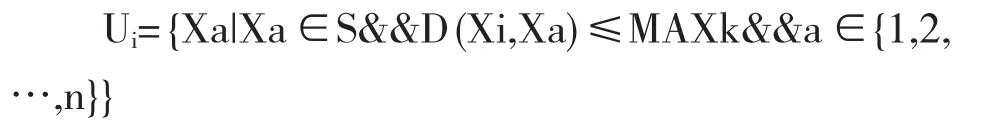
MAXk表示第i个对象与所有其他对象的距离按从小到大排序的第k个距离值.
定义5聚类输出集合SC={C1,C2,…,Ct,…,CK},其中K为聚类的簇数,Ct表示第t个类的对象集合.
3.2基本思想
k-NearestNeighborCluster(kNNC)的基本思想是通过每个点的邻居点的匹配,当两个点匹配数达到设置数目时,那么就判定它们是一个类的.
kNNC算法思想描述如下:
确定邻居点个数k和匹配点数目n.
(1)通过距离算法确定每个点的k个最进的邻居点.
(2)取出没有被划分的一个数据点,设定为类Cj的第一个点,并且把它的邻居点设为该类的初始邻居点.
(3)依次取出没有被划分数据点,用该点的邻居点与Cj的邻居点进行匹配,如果匹配到点的个数大于匹配点数目n,那么就将该点加入Cj类.
(4)重复步骤3,知道所有的点都被划分到一个类.
在该算法中,我们使用欧氏距离来计算两个点之间的相似度,欧氏距离公式如下:

其中D(Xi,Xb)表示点Xi到点Xb的距离.
算法kNNC(S,nn,nnm),S={X1,X2,…,Xn};
输入:n个数据对象集合S;
输出:K个聚类数据对象集合SC={C1,C2,…,Ct, …,CK};
Begin
Set nn,nnm;
k=1;
allcoord=n;//剩余需要聚类的点的个数
For i=1 to n do
begin
For b=1 to n do
Computer MAXk D;
Ui={Xa|Xa∈S&&D(Xi,Xa)≤MAXk&&a∈{1,2, …,n}};//找到所有点的k个最近邻居点
end;
Repeat
For i=1 to n do
If Xi∉Cj|| k=1 then
begin
Cj=Cj+Xi;
CNj=Ui;
allcoord--;
Break;
end;
for i=1 to n do
begin
if Xi∉Cjthen
begin
mn=match(CNj,Ui);
if mn>=nnm then
begin
Cj=Cj+Xi;
CNj=CNj+Xi;
allcoord--;
end;
end;
end;
until allcoord=0;
End;
在上面的算法中,nn为邻居点数目,nnm两个点邻居点匹配数.MINk为距离最小的k个对象.CNj为第j个类的邻居点集合.match(CNj,Ui)为第j个类的邻居点与第i个点的邻居点一一匹配的匹配数.
4 实验
4.1实验的数据集
数据集1:
从数据堂下载来的6200条微博数据.其中1—1000条是马航数据,1001-2000是昆明暴恐数据,2001-3000是反腐数据,3001-4000是两会数据,4001-5000是转基因食品数据,5001-6000是乌克兰事件数据,另外我们还加入了200条噪音数据.
处理数据:
(1)去除数据的无用符号,网址等;
(2)对数据进行分词;
(3)去除停用词;
(4)用BTM对数据进行建模;
数据集2:从UCI上下载的聚类数据集,一共有210条5维数据,数据分为3个类,每70条为一个类.
数据集3:从UCI上下载的聚类数据集,一共有600条60维数据,数据分为6个类,每100条为一个类.
实验采用准确率(Precision)、召回率(Recall)以及F值(F-Measure)来对比两个算法.
4.2邻居数与匹配数对kNNC的影响
我们首先使用数据堂下载的6200条微博数据对该算法进行实验,实验结果在下图中展示出来.
从图1、图2、图3中可以知道对于不同的邻居点数,匹配点数对他们的影响趋势是大致相同的.都是先随着匹配点数的增加然后达到一个最高点,最后下降.从上图中可以知道当邻居点为500时,匹配点数为130时,准确率达到最高.当邻居点为600时,匹配点数为150时,准确率达到最高.当邻居点为700时,匹配点数为160时,准确率达到最高.
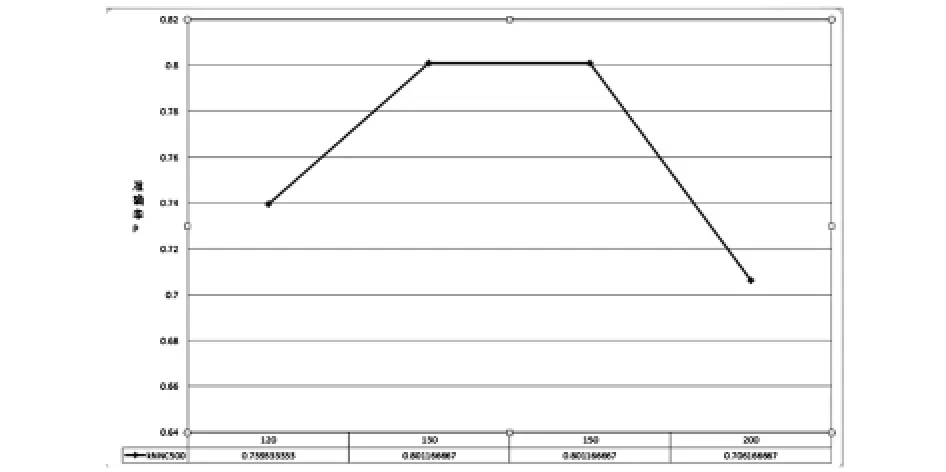
图1 邻居点为500时的匹配数对算法的影响

图2 邻居点为600时的匹配数对算法的影响
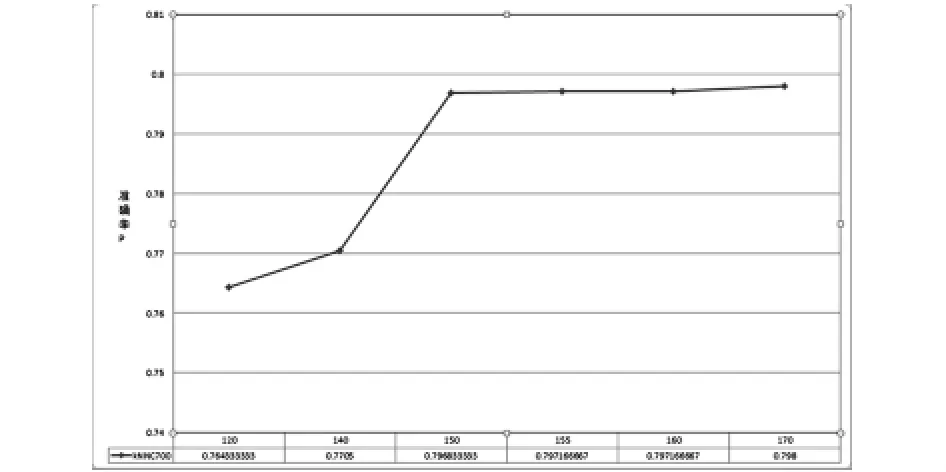
图3 邻居点为700时的匹配数对算法的影响
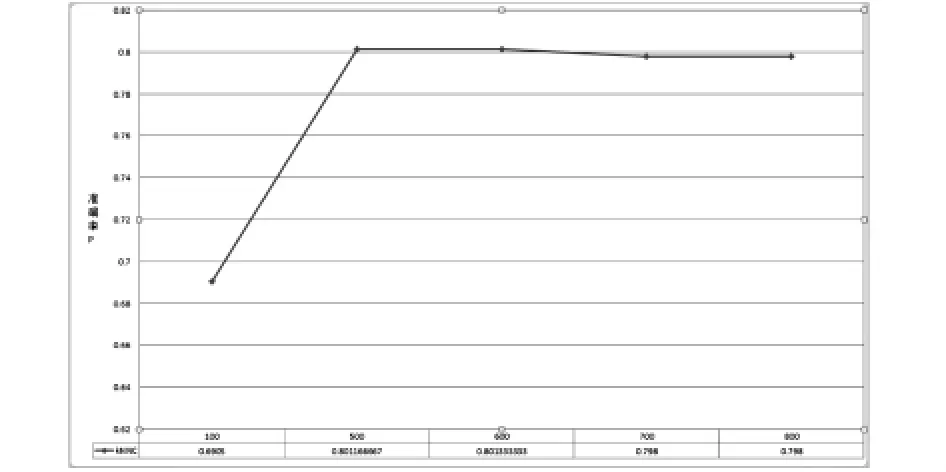
图4 邻居点数对算法的影响
图4给出了邻居点数对算法的影响,我们选取在各个不同的邻居点数下,最好的结果作为最终显示结果.从图中可知,随着邻居点数的增加算法的准确率成上升趋势,然后达到最高点以后,开始成下降趋势.从上图可知,当邻居点数设为600时,算法的准确率达到最大(0.801333).
4.3主题数的影响
对于微博6200条数据集我们使用BTM对其建模,我们对6200条数据,选取了不同的主题数用BTM建模.然后通过实验我们发现主题数对实验结果有着较大的影响.
从图5、图6、图7中可以看到随着主题数的增加,算法的准确率、召回率、F值都是先上升,达到一个最高点,然后下降.综合上图可知,在微博数据集上,当主题数达到7时,各项数值达到最优.
4.4其他实验
对于我们的算法能否正确的找到聚类簇数,我们做了下面三个实验:
1.对数据堂下载的6000条微博数据(weibodata)进行的实验(自己加入了200条杂数据).
2.对UCI下载的210条5维(uci210_5)数据进行实验.
3.对UCI下载的600条60维(uci600_60)数据进行实验.
实验结果在表1中给出了:

表1 算法确定的聚类簇数
从上表可知,该算法可以大致的找到数据的簇数.

图5 主题数对准确率的影响

图6 主题数对召回率的影响

图7 主题数对F值的影响
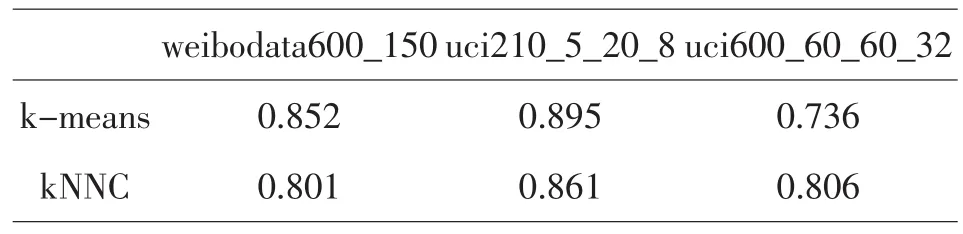
表2 算法的聚类准确率
在表2中uci210_5_20_8中的20_8表示当邻居点数设为20,匹配数设为8时,实验结果最佳.从表2可知,该算法的准确率很稳定,适合大部分的数据集.
5 结论
在这篇文章中,我们提出了一种基于kNN的聚类算法,该算法不需要预先设点聚类簇数,算法通过确定邻居点数和匹配点数,可以大致的找到聚类簇数.通过实验证明了该算法可以准确的将数据分类,并且具有稳定的准确率.该算法与k-means算法相比较,召回率有所提高,具有一定的实际应用价值.
参考文献:
〔1〕尹成祥,张宏军,张睿,等.一种改进的K-Means算法[J].计算机技术与发展,2014(10):30-33.
〔2〕姚宁,马青兰,张晶,等.基于AGNES算法优化BP神经网络和GIS系统的大气污染物浓度预测[J].中国环境监测,2015(03):3-5.
〔3〕徐克圣,王澜.一种自动获得k值的聚类算法[J].大连交通大学学报,2007(4):68-71.
〔4〕李双庆,慕升弟.一种改进的DBSCAN算法及其应用[J].计算机工程与应用,2014(08):72-76.
〔5〕项响琴,汪萍,李健.CLIQUE算法在信用卡审批模型中的应用研究[J].安徽建筑工业学院学报(自然科学版),2011,19(1):89-93.
〔6〕王志省,许晓兵.改进的基于SOM的高维数据可视化算法[J].计算机工程与应用,2013(17): 112-115.
〔7〕翁芳菲,陈黎飞,姜青山.一种基于KNN的融合聚类算法[J].计算机研究与发展,2007(44):187-191.
〔8〕廖礼.一种新的基于密度的聚类算法研究[D].兰州大学,2013.
〔9〕牛秦洲,陈艳.基于MCL与KNN的混合聚类算法[J].桂林理工大学学报,2015,35(1):181-186.
〔10〕仰孝富,齐建东,吉鹏飞,等.一种CF树结合KNN图划分的文本聚类算法[J].计算机工程与应用,2015(07):114-119.
收稿日期:2015-11-17
中图分类号:TP391
文献标识码:A
文章编号:1673-260X(2016)04-0014-04
