SIFT算法在木材纹理分类上的应用
2016-11-10陈宇臧美英李红波
陈宇 臧美英 李红波


摘要:为解决地板块纹理分类难度大的问题,提出了一种基于SIFT(scale-invariant featuretransform),尺度不变特征转换的地板块纹理分类方法,该方法首先采用SIFT算法提取地板块图像特征值,并采用K-means聚类算法降低关键点数目,得到用于分类的特征行向量,最后构造DEELM分类器进行分类.实验结果表明,该方法不仅减少了描述图片的关键点数目便于分类,而且提高了木材纹理分类的准确性,为地板块纹理分类的研究提供了一个新的思路.
关键词:木材纹理分类;SIFT算法;K-means算法;差分演化优化极限学习机
DOI:10.15938/j.jhust.2016.04.002
中图分类号:TP391.4
文献标志码:A
文章编号:1007-2683(2016)04-0007-06
0引言
随着人们生活水平的日益提高,越来越多的人在房屋装修时不单单追求美观而更加注重健康与环保,木地板具有无甲醛、防滑、美观、舒适等优点,受到了广大人民的喜爱,因此对木地板生产提出更大的挑战.如何提高生产效率和分选质量是实木地板生产过程中的一个重要环节,但自然纹理结构精细复杂,很难用数学公式精确表达,也是木材学术界的一大难题.国内外学者提出利用计算机视觉进行木材纹理分类,取得了不错的效果.我国对于木材纹理分类的研究起步较晚,初期主要是对国外的经验总结,优化传统的分类算法.现阶段我国的纹理分类技术发展较好,但也存在一定缺陷,主要由于实际应用的训练样本在个体之间存在着差异,导致分类结果的差异性较大.本文正是基于这种项目背景进行的木材纹理分类算法研究.
现实生活中每一幅图像中都包含着许多像素点,而且每幅图像中都具有其他像素点所没有的优点,这就是特征点,每个特征点都包含着大量的图像信息,可以说是整幅图片的骨架.David Lowe在1999年所提出,2004年完善总结的尺度不变特征转换算法(简称SIFT算法)是一种电脑视觉的算法,SIFT算法在特征点提取方面独具特色,它选择高斯残差在尺度空间上的极值点为特征点,并计算特征点局部邻域内的梯度方向直方图为描述子,对光线变化、尺度变化和视角变化都具有较强的鲁棒性,在计算机视觉领域得到一致认可.本文首先采用SIFT算法提取地板块图像特征值,并采用K-means聚类算法降低关键点数目,得到用于分类的特征行向量,最后构造DEELM分类器进行分类取得预期效果,不失为木材纹理分类提供一种有效方法.
1.算法原理
1.1 SIFT提取特征值
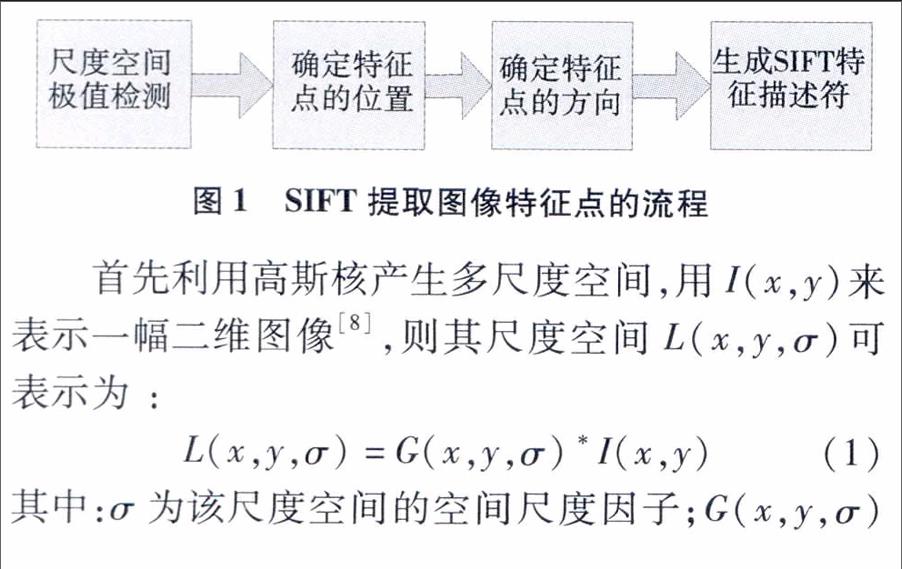
SIFT特征不只具有尺度不变性,即使改变旋转角度,图像亮度或拍摄视角,仍然能够得到好的检测效果.SIFT算法首先通过建立图像的尺度空间搜索该尺度空间中图像局部极值点,将所得极值点作为候选关键点,并将其中不稳定及对比度较低的点删除,从而最终确定关键点的主方向,进而生成每个关键点的特征描述符,SIFT算法提取图像特征点的流程如下图所示:
每一个采样点通过和它所有的相邻点相比较,这样就能够检测到DOG空间的局部极值点,如果该检测点为最大值或者最小值,则该点就作为图像在这个尺度下的一个候选关键点.
为了增强关键点的稳健性,需要去除低对比度的点和边缘点。
用海森矩阵求出主曲率,高斯差分算子的极值如果定义不好的话在横跨边缘的地方有较大的主曲率,而在垂直边缘的方向有较小的主曲率.
为了生成关键点描述子,让坐标轴方向与关键点的方向一致,以关键点为中心取16×16的窗口,最后在4×4的小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,这样就能形成一个种子点.对于每个关键点,16×16的邻域内可以形成4×4共16个种子点,每个种子点有8个方向的方向向量信息,因此每个关键点就获得了一个4×4×8=128维的特征描述符.
为进一步去除光照影响,将描述子向量归一化:
2.3 DE-ELM构造分类器
极限学习机(ELM)是一种单隐层前馈神经网络的学习算法,在算法执行过程中只需要设置网络的隐含层个数,不需要调整网络的输入权值以及隐元的偏置,就可以产生唯一的最优解.
由于ELM算法是在训练前通过设置网络隐含层的个数,训练过程中随机选取输入连接权值和阈值,最终获取目标值,这样会导致在选取中产生非最优或不必要的输入,且对未知测试数据响应较慢,针对这个问题利用差分进化算法(differential evolu.tion,DE)对ELM的权值进行优化,寻求全局最优解.本文提出用差分演化算法优化极限学习机(DE—ELM),来达到获得最优网络目的,实现较准确的分类,同时,差分演化优化极限学习机可以完成更紧凑的网络规模,且具有更好的泛化能力,速度较快,适用于木材纹理的分类实验.
差分演化优化极限学习机算法描述如下:
在实验过程中,训练、测试的时间与迭代次数、隐含层数成正比,继而选取木材纹理样本数NP=200,交叉概率cR=0.8,缩放因子F=0.02进行实验.实验发现当达到一定迭代次数时,目标值为0且保持不变,结果如图5所示.
当隐含层数确定,随着迭代次数的增加,目标函数最小值越收敛,当达到一定的迭代次数,目标函数最小值越稳定于O.而迭代次数一定时,增加隐含层数将可以降低算法的误差但会延长实验的完成时间,差分演化优化极限学习机算法的分类时间随隐含层比例增长,下图为迭代次数为20,样本数分别为20、40、80、100的分类时间随隐含层数增加的对比图:
同时为了使试验达到最佳效果,即误差最小,时间最短,又统计了随隐含层数增加的训练准确度如表1
在隐含层节点数为15时,DEELM算法达到误差最小点,并且趋于稳定.为了减短实验时间,因此,又在隐含层数为10的基础上增加隐含层数,设定隐含层数为11、12……,发现当隐含层数为12时误差最小,且时间相对最短.综上所述,选择隐含层数为12和迭代次数20的DEELM分类器进行分类.
3.实验结果
实验中选用了两种典型的地板块纹理进行分类,如图7所示,从图中可以看出,A类地板块的纹路横向走势,均匀分布,结构简单;B类地板块纹路环状走势,曲折蜿蜒,结构复杂.
实验中选取A、B两类样本共200个,每类100个,图片大小均为512。×512 bmp格式.首先在MATLAB平台上用SIFT算法分别提取每个样本的特征点,每幅图片生成一个K×128维(K为图片特征点的数目,每幅图片K值不同)的特征矩阵,此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响,对于每一个关键点,拥有3个信息:位置、尺度以及方向,完成特征提取的两类纹理图如下图所示。
利用K-means算法分别对每幅图片产生的特征矩阵进行聚类,得到描述显著目标的1×128维特征向量.选取其中100个地板块图像作为训练样本,其中A类训练样本50个,B类训练样本50个.将聚类后的数据保存在train_100之中,作为训练输入数据,如下图所示:
把训练样本输入DEELM分类器进行训练,本文所用方法与BP分类算法、SVM分类算法进行了比较,统计了测试样本数在20、40、80和100时的错误数,如表3.
从表3可以看出,不同算法在处理不同样本数的类别上的错误个数有较为明显差距,本文所用的DEELM分类器在分类本次样本上面的效果明显要优于BP神经网络SVM支持向量机.最后又统计了3种分类方法的准确率如下图所示,实验证明,DEELM分类器模型在木材纹理分类有一定的竞争性,效果明显.
4.结论
SIFT在图像的不变特征提取方面拥有无与伦。比的优势,该方法不但对于旋转、尺度缩放、亮度变化保持不变性,而且对视角变化、仿射变换、噪声也保持一定程度的稳定性,且该方法对特征点的个数和有效点的比例没有要求,当图片特征点数目不是很多时,甚至可以达到实时的要求.本文提出的基于SIFt木材纹理分类方法,利用SIFT算法提取木材图片的特征点,再用K-means聚类得到描述图片的特征行向量,最后训练DEELM得到分类器进行分类.实验结果证明了该算法适用于木材纹理分类,准确率高,有一定的实用性,为解决木材纹理分类问题提供了一种新的解决思路.
