高速移动环境下中导码插入的WiFi信道估计算法研究

彭春华， 姜植元， 吴 婧

（中南大学 信息科学与工程学院，湖南 长沙 410075）

随着高速铁路的迅猛发展，在飞速运行的列车上提供可靠、稳定的语音、数据通信已成为人们日益迫切的需要。目前高速列车上的公众通信质量并不乐观，提高通信服务质量是1个系统工程，有很多方面的问题亟待解决，信道估计就是其中之一。信道估计技术在某种程度上制约着移动通信系统性能的发挥，及时更新信道状态信息CSI（Channel State Information）对于扩大信道容量、降低系统误码率等具有重要意义。高速铁路中复杂多变的环境给通信技术带来了巨大考验，为此，研究适合高速移动环境下的信道估计技术是非常必要的。

Heath R.W［1］、朱文升［2］等提出了双 K 和单 K类的盲信道估计算法，其基本思想是：在不改变循环谱函数中频率变量的情况下，分析延迟变量z变换中的2个相关值而形成的算法，虽然估计精度较高，但是无论是单K还是双K算法，都需要构造多个Toeplitz矩阵，存在运算量大的缺点。李永会［3］等提出了一种适用于高速率和高速移动环境下的信道估计方法，通过利用经历相同衰落的两个独立信道联合估计出信道的冲激响应值，算法的优点是不需要利用导频符号，可以应用于高维的调制方式，但在高速移动的环境下，码字之间的正交性将遭到破坏，其应用也将受到限制。Myung［4］等使用Kalman滤波器实现半盲信道估计算法，然而这种算法是在假定信道变化较慢或是不变的条件下，因此这类算法不适用于快衰落信道。

文献［5］建立了信道估计凸优化模型，文献［6］系统而全面地总结了循环前缀的完整性对信道估计及接收端均衡恢复的影响。但此二者主要是基于时域上的研究。文献［7］给出了1个在LS估计框架下导频序列数量的选择对信道估计性能影响的方法，但在时域上的估计性能涉及很少。赵旺兴［8］等提出了在OFDM中循环前缀频域序列用于最小二乘信道估计的方法，充分利用循环前缀的时域和频域特征，但在高速移动环境下的性能还待进一步研究。

在高速移动环境下，传输信道由于时间选择性和频率选择性，使得信道状态在时域和频域上同时变化，如果不能在时域和频域上对信道进行实时跟踪与估计，会带来较大的估计误差，严重恶化系统的性能。为了实现高速移动铁路环境下信道的实时估计，本文结合Kalman滤波器提出了1种时频结合的WiFi信道估计方法。

1 改进的信道模型

1.1 信道特征分析

在移动通信的研究中，为了分析信道估计算法的性能，系统信道模型的搭建是不可或缺的一步。为了建立适用于高速铁路环境下的信道模型，首先要了解高速铁路环境下信道的特征。在高速铁路环境下，其传输信道除了具备基本移动信道的特征之外，还具备一些独有的特点，主要有：

（1）高衰耗

高速移动列车的车体是由完全封闭的金属车窗和面板组成，这样一个封闭的车厢可以看作一个法拉第金属小屋。其带来的路径损耗可达约20dB。

（2）列车移动速度变化引起信道的快速变化

一般移动通信系统中通信主体的移动速度远远达不到高速移动列车的运行速度。随着移动主体速度的增加，导致接收信号的多普勒频移增加，引起接收信号的快速衰落。在这种条件下，无线信道质量急剧恶化，传统的信道均衡技术，在这种快衰落信道下将很难实现信道的预测和均衡。而且列车由于进站等因素引起的移动速率极大变化导致无线信道的可用带宽和越区切换时间间隔变化等，也带来了切换、均衡、功率控制、信道估计等技术在高速移动环境下应用的挑战。

（3）运动路线和运行时间的可预测性

高速运行列车一般按照相同路径运动并在特定位置（车站）停止，运动时间也相对稳定。针对这一特点，可以预测列车移动网络的信道基本特征，并可据此预先进行策略设置。

（4）铁路沿线无线信号可实现视距传输

高速铁路沿线地形平坦，地面起伏较小，方便部署定向天线，实现视距接入。同时其周边区域复杂多变，经常通过平地、山区、隧道、路堑和深沟等不同的地形环境，各种无线信号的强度和覆盖范围变化较大，多径传输问题严重。因此，一般的公众移动通信网不适合于这种传输环境。

1.2 信道模型的改进

目前，广泛应用的信道模型主要是瑞利衰落模型和莱斯衰落模型。而在高速移动环境下，由于恶劣的周边环境带来多径效应以及列车快速移动导致的多普勒频移的影响，接收端收到的信号是直射波、反射波、散射波和绕射波等的叠加信号，而且不同场景所对应的信道特性也不同。为更好地描述高速铁路环境下的信道特性，引用COST207RA信道模型［9］，对其改进后，得到改进的COST207RA信道模型，见表1。改进后的模型一共有7个子径，原来的第1子径被分成了2个子径，分别为视距信道和瑞利信道［10］，根据COST207标准的规定，视距信道采用莱斯谱描述，其余6个子径均采用经典瑞利谱描述，功率也同时均分在第1、2条子径上。

表1 改进的COST207的RA信道模型参数

2 中导码信道估计

在高速移动环境下，由于周边环境的复杂多变以及列车的高速行驶等，发送的数据信号在无线传播时受多径效应、阴影衰落和空间传播损耗等影响而产生衰减，使得数据信号的幅度、相位等发生改变。在接收端，为了恢复出原始的发送信号，需要利用信道估计技术估计出信道状态信息。信道估计的精确度对于通信系统而言是至关重要的，主要取决于信道估计算法、通信环境和终端的移动速度等因素［11］。

为论述中导码信道估计方法，以IEEE802.11a为例，先说明基于前导码的信道估计方法CEOP（Channel Estimation On Preamble），此算法利用前导码（Preamble）估计出Preamble位置处的信道状态信息，再结合插值或滤波等计算出所有符号处的信道冲激响应值。

CEOP的帧结构见图1，由前导码、SIGNAL域和数据部分组成。图1中，t1～t10代表10个短训练序列，T1、T2代表两个长训练序列，GI为保护间隔，DATA代表数据符号。

根据图1的帧结构可以得知，利用CEOP进行信道估计的信道传输函数Hf可以表示为

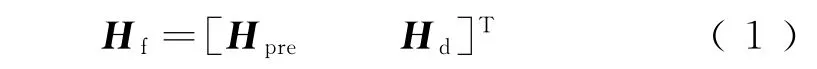
式中：Hpre代表前导码位置处的信道传输函数；Hd代表传输数据位置处的信道传输函数。

中导码信道估计MACE（Midamble Aided Channel Estimation）是在CEOP基础上的改进，在原OFDM帧中，前导码中的长训练序列T1、T2用来进行信道估计，将此训练序列进行全部或部分复制作为中导码，周期性地插入到数据符号中。插入的中导码可以是长码，也可以为短码，长码有两个OFDM块（8 μs）长度，见图2，短码长度为1个OFDM 块（4μs），见图3。

图1 CEOP的帧结构图

图2 长码结构的MACE帧结构

图3 短码结构的MACE帧结构

图2和图3中，Midamble表示被等间隔插入到数据符号中的中导码，用于估计信道状态值。因此，MACE的信道传输函数可以为

3 改进的中导码信道估计算法

本文信道估计技术应用场景：在高速铁路中，铁路沿线每隔500～1 000m布置一个无线接入点AP（Access Point），每节车厢放置2～3个路由器［12］，以保证可靠地传输数据，车－地通信以及车内通信均采用802.11a协议。

在高速移动状态下，无线移动信道不但具有时间选择性同时还具有频率选择性，信道的时域特性和频域特性都处于变化当中，简单的中导码估计无法获得信道的频域变化量。为此，结合导频估计，得到改进的中导码信道估计AMACE（Advanced Midamble Aided Channel Estimation）方法，将导频估计、中导码估计和Kalman滤波进行有效结合，给出1种适用于高速铁路环境下时域频域相结合的信道估计算法，方案见图4。

图4 信道估计方案

图4中，Hm为利用MACE得到的信道估计值，Hp为利用导频子载波进行估计的信道估计值，Hk表示由Hm和Hp通过Kalman滤波器后获得的信道估计修正值。

3.1 利用导频的估计

基于导频的信道估计方法是改进中导码信道估计算法的基础，而利用基于导频的信道估计方法进行信道估计时，主要步骤为：

Step1 根据移动信道的特征，进行导频结构的选择。

Step2 导频位置处信道状态信息的获取。

Step3 通过导频位置处的信道状态信息，估计所有符号处的信道状态信息。

导频的选取决定信道估计的精度和开销。在进行导频结构选取时，主要考虑一方面是要确保信道估计的精度，提高系统的性能；另一方面要尽量降低系统的开销，提高资源的利用率。常用的导频一般有块状、梳状和网状导频3种。梳状导频符号在时间上是连续的，比较适用于快衰落信道。

在高速铁路环境下，信道的状态信息是时变的，即使相邻的两个OFDM符号的信道冲激响应也会存在很大差异。Woong等针对3种导频结构进行了比较［11］，仿真结果表明：在快速移动环境下，利用梳状导频进行信道估计要优于其它两种。基于此，在高速铁路环境下梳状导频结构被选为导频的插入方式。梳状导频结构见图5。其中，Plj表示导频子载波lj位置处插入的导频，其中j＝1，2，…，n，n为插入导频的总个数，lj－lj－1＝d，d为两个相邻导频之间的间隔。

图5 梳状导频结构

假设导频为等间隔分布，利用导频，可通过一阶线性插值算法求出任意子载波处的信道估计值

式中分别为利用导频子载波进行信道估计得到第n个OFDM符号上第lj－1、lj、x 个子载波处的信道估计值；lj－1、lj为导频子载波，lj－1＜x＜lj且lj－lj－1＝d；k1，k2都是常数且满足0≤k1，k2≤1。

3.2 全部信道响应值的获取

根据Kalman滤波器的状态方程和输出方程，可以建立Kalman滤波方程

式中：H（i，k）表示第i个OFDM符号，第k个载波位置处的信道传输函数；Y（k）为H（i，k）的观测值，即输出值；A（i，k）为H（i－1，k）与 H（i，k）状态变量转移矩阵；C（i，k）为 H（i，k）与Y（i，k）之间的转移矩阵；V（i，k）为状态噪声向量；W（i，k）为观测噪声向量。假设当前状态是i，则改进的中导码信道估计算法具体更新和迭代过程如下 ：

Step1 第i时刻第k个子载波上信道的状态值估计值（i，k）为（i－1，k）经过一个乘法器得到的值，即（i，k）＝Α（i，k（i－1，k），其中（i，k）为i时刻第k个子载波上的信道状态估计值。

Step2 在忽略噪声V（i，k），W（i，k）的影响时，上一时刻的信道状态估计值（i－1，k）经过两个乘法器的作用而获得信道状态的输出估计值（i，k），即（i，k）＝C（i，k）Α（i，k（i－1，k）。

Step3 用误差e＝Y（i，k）－（i，k）修正信道的状态值估计值（i，k），即（i，k）＝Α（i，k）（i－1，k）＋Kj［Y（i，k）－（i，k）］，进而求出下一状态的信道值估计值（i＋1，k）。其中Kj为Kalman滤波器的增益矩阵，（i－1，k）和（i，k）的初始值分别为Hm和Hp。

Step4 依次不断迭代最后求出所有符号处的信道状态估计值，完成信道估计。

由于中导码的引入，可以把处于前导码与中导码、中导码与中导码之间的子载波信道状态看成不变，所以C （i，k）等于单位矩阵I，于是式（4）可简化为

根据矢量Kalman滤波算法，可得到基于矢量Kalman滤波算法的信道估计过程：

预测矩阵为

最小预测MSE矩阵为

式中：M（i，k）为在第k个子载波i－1时刻的条件下，第k个子载波i时刻的最小预测 MSE矩阵值；Q（i，k）为V （i，k）的协方差矩阵；P（i，k）为最小 MSE矩阵。

令

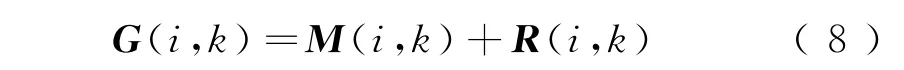
式中：R（i，k）为W（i，k）的协方差矩阵。

则Kalman增益矩阵为

式中：K（i，k）为Kalman滤波器在第k个子载波i时刻的增益矩阵值。

令

则修正矩阵为

最小MSE矩阵为

3.3 Kalman滤波器参数估计

在实际应用中，系统参数Α（i，k）、Q（i，k）、R（i，k）以及Kalman滤波的初始值待定，下面说明待定参数的估计。

（1）参数Α（i，k）的估计

由于状态变量时刻变化，所以要对Α（i，k）进行实时估计以降低估计误差。Α（i，k）表示状态变量转移矩阵，假设各个子载波之间不相关，计算方法为式中：diag（）为对角矩阵；a（i，k）为对角矩阵对角线上的元素值；Hp（i，k）为第i时刻第k个子载波利用导频子载波估计得到的信道状态值。

（2）参数Q（i，k）的估计

Q（i，k）为V（i，k）的协方差矩阵，计算方法为

当子载波之间不相关时

式中：σ2（v（i，k））为过程噪声V（i，k）的方差

于是有

式中：a（i，k）可以由式（14）求得。

（3）参数R（i，k）的估计

R（i，k）为观测噪声向量＾W（i，k）的方差矩阵

当子载波之间不相关时，R（i，k）为对角阵

式中：σ2（v（i，k））为观测噪声＾w（i，k）的方差。

（4）Kalman滤波初始值

信道的初始值为

4 仿真与分析

为评估所提算法进行信道估计的误符号率SER性能，在COST 207RA信道模型下进行了Matlab仿真分析。设定系统工作频率f＝5GHz，系统带宽B＝20MHz，数据子载波数N＝48，导频子载波数Np＝4。OFDM数据符号长度T＝4μs，其中数据符号长度Td＝3.2μs，循环前缀长度TGI＝0.8μs，长训练序列符号长度为8μs。采用Gray编码的矩形16QAM调制方式，数据符号数量为106个，每个OFDM帧包含200个数据符号。假设16QAM符号能量与中导码符号能量相等，系统同步已完成，并且频偏值为0。COST 207RA信道模型由抽头延迟线TDL（Tapped Delay Line）模型和过滤后的高斯白噪声FWGN（Filtered White Gaussian Noise）模型产生，采样周期Tsam＝0.1μs，信道衰落功率归一化为1。中导码采用两种插入间隔：短间隔SI（Short Interval）和长间隔LI（Long Interval）。SI每间隔10个数据符号插入1个Midamble，LI是每间隔20个数据符号插入1个Midamble。

图6（a）为每间隔10个数据符号插入1个中导码，即短间隔插入，调制方式为16QAM，移动速率为200km／h的条件下，误符号率SER 与信噪比SNR之间的曲线关系图；图6（b）是在与图6（a）相同条件下，采用长间隔LI方式插入中导码后SER与SNR的关系曲线。

图6 SER与SNR之间的曲线关系图

图6（c）是短间隔插入，调制方式为16QAM，移动速率为300km／h的条件下，SER与SNR之间的曲线关系图。图6（d）是在与图6（c）相同条件下，采用长间隔LI方式插入中导码后SER与SNR的关系曲线。从图6（a）、图6（d）中可以看出，在同条件下，AMACE方式比CEOP方式有更好的估计性能。在SNR＞10dB时，AMACE方法比MACE方法有较好的信道估计性能，但随着SNR的进一步增大，这种优势不断减弱。随着移动速度的提高，比较AMACE与MACE，可以看出：以短间隔插入中导码比长间隔插入有更好的信道估计性能，但当SNR＞30dB后，AMACE相对MACE而言，没有明显优势。

为了进一步分析插入中导码后系统的性能，引入中导码插入比参数k

图7是调制方式为16QAM，移动速率为200km／h时，采用MACE方式，不同中导码插入比为k时，SER与SNR之间的曲线关系。从图7可见，当k越小，同条件下，SER越低，其估计性能越好，插入的中导码数越多，传输效率越低。要兼顾估计性能和传输效率，需要寻找合适的插入比。

图7 插入比变化时SER与SNR之间的关系（16QAM，200km/h）

为此，在不同的移动速率下，对采用不同插入比的中导码，分别仿真其信道估计性能。图8为调制方式为16QAM，SNR ＝20dB，SER ＝10－2时，采 用MACE方式，中导码插入比k与移动速率的关系。从图8可见，当移动速率为200km／h时，k＝20。但要获得理想的估计性能，要适当减少k值。

图8 移动速率与中导码插入比之间的关系（16QAM，SNR=20dB，SER=10-2）

5 结束语

为解决高速移动环境下时变信道的估计问题，本文提出插入中导码的信道估计方法。仿真结果表明，中导码的引入，使得信道估计性能比利用前导码估计的要更具优势。为进一步提升估计性能，结合时域和频域估计，提出了Kalman滤波算法，把中导码和导频估计值进行滤波，得到精确度更高的信道估计值。仿真表明，Kalman滤波提高了估计精度，更适用于高速移动环境下的信道估计。但随着移动速度的增加，要维持一定的估计精度，中导码的插入间隔将变短，将导致数据传输效率的降低。如何让系统自适应选择中导码插入比，兼顾估计精度和传输效率，是下一步研究的重点。

参考文献：

［1］HEATH R W，GIANNAKIS G B.Exploiting Input Cyclostationarity for Blind Channel Identification in OFDM Systems［J］.IEEE Transsction on Signal Processing，1999，47（3）：848－856.

［2］朱文升，李有明，俞建定，等.基于循环平稳特性的OFDM盲信道估计算法［J］.宁波大学学报：理工版，2010，23（4）：62－66.ZHU Wensheng，LI Youming，YU Jianding，et al.Cyclostationarity－based Blind Channel Estimation Algorithm for OFDM System［J］.Journal of Ningbo University：Science and Technology Edition，2010，23（4）：62－66.

［3］李永会，张其善，李道本，等.一种适用于高数据速率和高速移动环境的新型信道估计方法——双正交通道信道估计方法［J］.电子学报，2002，30（4）：467－470.LI Yonghui，ZHANG Qishan，Li Daoben，et al.Novel Channel Estimation Method Applied to High Data Rate and High Speed Mobile Communications－channel Estimation by Using Two Orthogonal Channels［J］.Acta Electronica Sinica，2002，30（4）：467－470.

［4］MYUNG S B，YOUNG H Y，HYOUNG K S.Semi－blind Channel Estimation and PAR Reduction for MIMO－OFDM System with Multiple Antennas［J］.IEEE Transaction on Broadcasting，2004，50（4）：414－424.

［5］KOIKE A T，MOLISCH A F，DUAN C J，et al.Capacity，MSE and Secrecy Analysis of Linear Block Precoding for Distributed Antenna Systems in Multi－user Frequency Selective Fading Channels［J］.IEEE Transsactions on Communications，2011，59（3）：888－900.

［6］SU B.Blind Channel Estimation Using Redundant Precoding：New Algorithms，Analysis and Theory［D］.California：Institute of Technology Pasadena，2008.

［7］ZHAO W X，FANG F.A Diverse Proof of OFDM Channel Estimation Comparing CP－sequences and Training－sequences Methods Under LS Frame［C］／／Proceedings of IEEE International Conference on Information Theory and Artificial Intelligence Computing.New York：IEEE，2011.

［8］赵旺兴，万群，陈章鑫.基于OFDM循环前缀LS信道估计的构造方法［J］.通信学报，2013，34（3）：175－182.ZHAO Wangxing，WAN Qun，CHEN Zhangxin.Novel Restructuring Method for CP－based LS Channel Estimation in OFDM System［J］.Journal on Communications，2013，34（3）：175－182.

［9］HUISH P W.A Review of the Radio Propagation Work Undertaken Under the COST 207Programme［C］／／Proceedings of IEE International Colloquium on Propagation Factors and Interference Modelling for Mobile Radio Systems.London：IEE，1988：1－4.

［10］施荣华，蒋泽艳，彭春华，等.一种时频结合的中导码信道估计算法［J］.计算机应用研究，2013，30（6）：1 794－1 797.SHI Ronghua，JIANG Zeyan，Peng Chunhua，et al.Timefrequency Combination Channel Estimation Algorithm Based on Midamble［J］.Application Research of Computers，2013，30（6）：1 794－1 797.

［11］WOONG C，SANG I K，HYUN K C，et al.Performance Evaluation of V2V／V2ICommunications：the Effect of Midamble Insertion［C］／／Proceedings of 1stInternational Conference on Wireless Communication，Vehicular Technology，Information Theory ＆ Aerospace Electronic Systems Technology（Wireless VITAE）.New York：IEEE，2009：793－797.

［12］彭春华，蒋新华.高速移动环境下提高WLAN有效吞吐量方法的研究［J］.铁道学报，2012，34（1）：54－59.PENG Chunhua，JIANG Xinhua.Research on Improving the Effective Through Put of WLAN in High－speed Mobile Environment［J］.Journal of the China Railway Society，2012，34（1）：54－59.