让高中数学“难题”越做越“简单”

☉浙江省黄岩中学黄仙萍

让高中数学“难题”越做越“简单”

☉浙江省黄岩中学黄仙萍

在现行的高考模式下，高中数学在高考科目中占有重要的地位，这已经成为广大教师和学生的共识.解题教学是高中数学教学中的重要组成部分，笔者在平时的高中数学教学中发现，部分学生对于考题给出的标准答案容易看懂，但是难于理解答案中为什么会采取如此巧妙的处理手段与方法，在自己处理数学问题时感觉困难重重，其实每道数学题解法的背后都蕴藏着丰富的数学思想方法，只要对数学难题进行深入的思考与分析，便能将“难题”做得“简单”点！

一、思路受阻时转换新思路，回归起点，体现“简单”

在高中数学解题中，“无章可循，无路可走”可称为“难”题，当我们按照常规思想解决数学难题受阻时，不妨考虑采取“倒退”的思想，灵活转换新思路，从最原始的数学概念、数学原理为起点进行分析与探究，反而会实现“有章可依，有路可走”，对于高中数学教师值得注意的是，在解题教学中应该尽可能地避免“演播式”的教学，只是满足于将解题的每一步清晰地呈现给学生，忽视进行解法缘由的探索与分析，这对学生解题能力的提升成效不大.

分析：本例是一道高考试题中的一小问，部分学生接触到题目时不知所措，将题设中给出的条件进行变化，始终不能把握住解题的要领，主要体现出数学概念与解题目标不清晰，解题的思路也比较混乱.其实本题只要回归起点，从数列的概念出发进行处理：

二、洞悉命题意图，借数学背景打开解题通道，体现“简单”

随着新课改的不断深化，数学试题考查的形式也是推陈出新，命题专家们比较喜欢针对于数学文化背景中所蕴藏的问题进行加工，重新赋予新的内涵与意义，具有明显的数学新意.掌握丰富的数学背景知识能够有效实现从“生疏”到“熟悉”的转变，消除学生遇到难题而畏惧的心理障碍，有助于获取便捷的解题通道.

分析：根据题设提供的信息多数学生以角度为自变量，利用三角函数的有界性知识进行求解，运算量较大，计算繁杂，费时费力，效率不高.实际上命题者的意图是引入“阿波罗尼斯圆”进行处理，了解这样一个数学背景，该题就能够有效地将三角问题解析化：构建直角坐标系xOy，如图1所示，令A（-1，0），B（1，0），C（x，y），结合题意可得（x-3）2+y2=8，则动

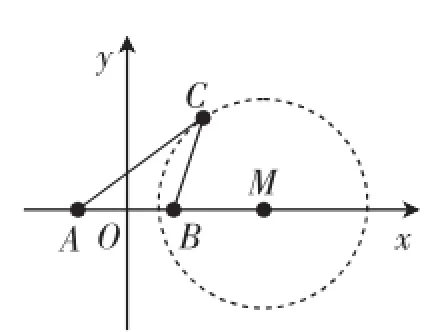
图1

在新课改背景下，高考数学命题考查倡导“多一点想，少一点算”的指导思想.本题中直接利用三角函数等知识也可以求解，但是与利用“阿氏圆”进行处理相比来说比较烦琐点.其实数学背景包含：文化背景、生活背景、学科背景、图形背景等等，可以说数学背景的有效揭示，为数学解题打开“一个通道，一扇窗”，让解题变得简便易行.

三、注重思维的灵活性，活用题设条件减少数学运算，体现“简单”

数学解题实质上是根据题设条件，借助于合理的数学变形，实现条件与结论之间的关联，达到预期的目标，在这一过程中涉及“等价转化与非等价转化、特殊与一般的转化、数形结合”等数学思想，在实际问题处理过程中，常常遇到非常规的难题，这就需要学生发挥思维的灵活性；解析几何是高中数学教学中的重点和难点，灵活运用题目中提供的已知条件，大大简化解题过程，避免复杂的数学运算，提高解题效率.

分析：本例是根据高考真题改编而来，若采取代数方式进行处理，运算相当复杂，而且部分学生难以准确完成.若能紧扣题设中的已知条件，加以灵活运用，即可简化解题过程，减少数学运算，提高解题的正确率.具体为：根

图2

代入椭圆方程可得［（1+λ）x-λ］2+2（1+λ）2y2=2，［（1+ λ）x+1］2+2（1+λ）2y2=2λ2.综合两式简化1，即动点M的轨迹为椭圆，且焦点坐标分别为（-1，0），

从上述解法中可以感觉到“简捷利落”，关键是灵活运用题设中AF1∥BF2这样一个条件，借助于向量的定比分点数学规律进行处理，采取待定系数法探讨出动点M的轨迹.当然本题根据解决目标“MF1+MF2为定值”也可以联想到点M轨迹可能为椭圆，在某种程度上明确了解题思路的大方向，有助于快捷、高效解题.可见，在解析几何问题中，合理、巧妙地运用题设条件，表明感觉增加思维量，实际上大大减少运算量，正确率大大提升.这也提醒我们一线数学教师，在平时的课堂教学中，不断引导学生进行归类、分析、提炼、总结，让学生成为学习的有心人，促进学生处理实际问题能力的提升.

四、坚持在反思中总结与联想，实现解题方法的迁移，体现“简单”

部分学生奉行的“一题一法，灵活多变”的思想导致形成“谈数色变”的怪圈，主要原因是这部分学生在数学中不注重解题方法的归类、反思和总结.这也提醒我们数学教师在平时的教学中应该引导学生善于追根究底，探寻数学知识与方法之间的联系和规律，在反思中总结与联想，逐步实现“一题多解、多解归一、多题归一”，达到解题方法的迁移，解题能力的提升.

分析：本题题设内容简洁看似简单，其实并不容易解决，根据题设信息和所求问题，学生倾向于利用“拼凑”的方法进行处理，成功解题主要取决于“硬”配凑的这种特殊情形下的配凑是行之有效的方法，但是相对多数常规思维的学生来说还是比较困难的！其实3，2α-β=-4，则α=-1，β=2！

这里使用的“待定系数法”是数学课本教材中常见的一种解题方法，几乎每个学生都很熟悉，但是这种最常见的方法却容易被忽视，主要是学生对这种方法本质认识不到位，缺乏由“线性系数形式”向“幂结构形式”的联想意识，缺乏数学解题方法的迁移能力！

总之，对于高中学生而言，解题能力强通常是数学学得好的重要体现，但是数学教学并不仅仅是解题教学，学生也不是机械的、被动的“数学解题匠”.作为一线的高中数学教师，应该着眼于学生数学综合素养的提升，合理构建自主合作、轻松愉悦的情境，让学生感悟数学的魅力，自觉成为数学学习的研究者和受益者；在具体实施的习题教学中，尽可能地引导学生展示数学解题的思维过程，在清楚“如何做”的基础之上，更加要理解“为何这样做”，让学生感悟解题的思维过程，避免机械、盲目地生搬硬套数学公式；注重引导学生“察言观色”，进行合理的联想与思考，探寻多角度解决问题的途径，学会“举一反三、触类旁通”，培养学生发散思维能力，让学生在不断的总结反思中，真正达到“熟能生悟、悟中生巧、巧而创新”的理想境界.G