PBL模式下的高中数学微课教学研究
——以“不等式与数列求和教学”为例
2016-05-15江苏省口岸中学高国圣
☉江苏省口岸中学高国圣
PBL模式下的高中数学微课教学研究
——以“不等式与数列求和教学”为例
☉江苏省口岸中学高国圣
随着新课程改革的日益深入,传统的“满堂灌”“填鸭式”教学模式已经逐渐被“问题探究式”教学模式取代,PBL模式是一种新型教学模式,这是一种以问题为中心的教学模式,教师在“问题中心”下指导学生进行深入思考,结合自己所学知识提出新问题.微课教学与PBL模式相结合,能够有效提高课堂教学学习效率,也有利于培养学生的自主学习探究能力.
一、PBL模式与微课教学形式分析
1.PBL模式
PBL模式是一种以问题为基础的教学方法,教师围绕教学目标,在问题指导下设计教学步骤,PBL模式下的课堂教学主要分为四个阶段:课前准备阶段、课堂阶段、课后自学阶段、课堂总结评价阶段.下面我们将具体分析这种教学模式下的教学四阶段:(1)课前准备阶段.首先让学生了解PBL模式有关知识、特点,教授学生学会使用这种教学模式发现问题并解决问题,增强其对PBL模式的认识与理解.PBL模式最突出的一个特征就是学生进行分组学习,学生分组时,应将小组规模、学生搭配及组内结构等考虑进去,小组人数最好控制在6人左右,搭配好性别、性格及成绩比例,将知识与能力互补互助特点体现出来,小组学习讨论时应明确分工.[1]教师采用PBL教学模式,需要创设一种学习情境,在情境中教学,引导学生在情境中发现问题,并围绕问题获取知识与能力,教学情境中问题应精心设置,最好具有实践性、复杂性及层次性.(2)课堂阶段.教师将课本中需要解决的问题蕴含到现象或事件描述中,并结合有关教学大纲及问题编制成案例资料,然后将这些案例资料按照小组形式分发给学生,组长检查案例中是否有不懂的概念或术语,其次,进行案例解读,并从案例中提取问题,接着提出假设,从问题出发提出问题解决的假设,将可能涉及的原因及方法、后果等提出来,第四步是确定需要增加的案例资料,第五步是最终确定学习目标,小组成员经过商议后得出一致想要解决的问题,第六步是制定较详细的学习计划,分配给各小组学习任务,确定下一步学习内容及任务.[2](3)课后自学阶段.学生根据分配好的学习任务,通过查阅书籍、上网等方式收集资料,进行自主学习.(4)课堂总结评价阶段.该阶段主要是展示报告学习效果、反思并评价.
2.微课教学
微课主要是指那些以教学设计思想为基础,利用多媒体技术在短时间内针对性讲解某个知识点的视频或者是音频.微课在实际教学教育过程中,讲授内容大多数呈现出“点”状、碎片化,微课是新时期新技术的产物,是课堂教学的有效补充形式,有利于学习者进行个性化及深度化学习.教师使用微课教学形式,常常使用手机、相机或者是DV等设备进行录制与拍摄,也可以使用有关软件将其制作成视频或音频.
二、PBL模式下的高中数学微课教学实施策略分析
1.PBL模式下的高中数学微课教学实施策略陈述——以数列求和教学为例
这里以高中数学中的数列求和知识作为实例进行分析,首先,设置好要探究的课题:等差数列的前n项和,根据这一课时制定教学目标、教学重难点.然后,采用PBL教学模式:第一步设疑自探,教师在课堂教学中先创设一个问题情境,将17世纪莫卧儿帝国皇帝沙杰为爱妃建造的泰姬陵作为情境导入课堂,泰姬陵主要使用纯白大理石砌建,是世界古建筑的七大奇迹之一,其中陵寝被宝石镶嵌,图案精美绝伦,陵寝是一个三角形图案,它被大小相同的宝石镶嵌而成,一共有100层(如图1所示),教师这时提出问题:同学们知道这个图案一共用了多少颗宝石吗?

图1
教师应使用这个情境问题引出所要讲解学习的知识,吸引学生注意力,激发学生学习兴趣,问题情境应采取先进多媒体手段,以微课形式展示出来,可以在正式上课前让学生观看有关这个建筑图案的小视频.[3]接着教师提问学生:看到这个问题情境,同学们能想到哪些数学问题呢?学生会就这个问题进行思考,并提出了新问题,例如,这些镶嵌宝石有什么规律吗?也有的想到了怎样求1+2+3+…+100=?等差数列前n项和能使用高斯算法求解吗?这样教师帮助学生梳理问题,提出本课的学习目标.第二大步就是让学生分组合作讨论,小组成员先分层讨论,然后再群体讨论,并展示自己讨论成果,明确各小组课堂任务,选派不同小组在黑板上展示问题的解决方法,通过一系列问题探讨分析后,得出等差数列前n项和公式.
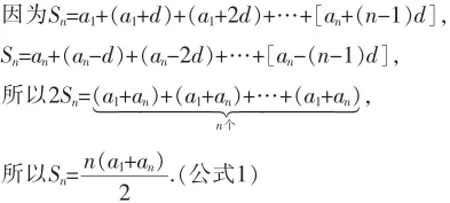
接着教师还要给学生进行有关知识补充,学生在此之前学习过an=a1+(n-1)d,因此,等差数列的另一种变形公式为
2.PBL模式下的高中数学微课教学实施策略陈述——以不等式为例
PBL教学模式以促进学生终身发展、培养学生创新能力为最终目标,因此,教师在课堂教学过程中,可以有目的、有针对性地引导学生就教师设置好的问题再提出新问题,通过改变条件、结论等形式来反复编题,培养学生逐渐形成良好数学思维,学生能逐渐掌握常用的数学方法解题,例如,分离常数法、配方法及数形结合法等,这里我们以高中数学中的不等式知识为例进行探讨分析,将PBL模式与数学方法分离常数法应用到不等式教学及解题过程中.[4]
针对这个题目,教师向学生提出问题:这个是什么函数?如何求这个函数的最值?求值方法的灵感来源是什么?
学生会依次回答问题,并得出结果、结论:这个是分式函数,分式函数求最值要先进行变形,从而得到f(x)=示,接着教师顺着学生受基本不等式启示引导学生由等号成立,所以当x=1时,函数的最小值为9.
教师解答出答案之后,再提出这道题的变形是非常重要的,那么哪些数学题也能这样变形呢?让学生以小组形式进行讨论,然后以微课形式在课堂上展示出来,最后进行总结得出结论.综合上述分析及具体题目解答,能够看出PBL模式是一种以问题促进问题的教学模式,学生只有自主探究、剖析数学知识及习题,才能提出有效问题,采取数学思维及数学方法成功解决问题.
三、结束语
PBL模式符合高中学生的认知规律及思维特征,也积极响应了新课程标准倡导的“自主”、“合作”等教学学习理念,是一种高效科学的教学方法.高中数学教师应在实际教学中就具体问题设置合理情境,引导学生提出问题,并激发学生的学习兴趣与积极性,使其自主学习探究、勇于提出疑问、学会反思,从而逐渐提升自主学习能力及创新能力.F
