山穷水复疑无路，柳暗花明又一村——例谈参数方程在高中数学中的运用

☉江苏省宜兴中学欧贺宏

山穷水复疑无路，柳暗花明又一村
——例谈参数方程在高中数学中的运用

☉江苏省宜兴中学欧贺宏

参数方程是曲线上点的位置的另一种表达形式，它把曲线上的点的横、纵坐标分别通过参数直接表示出来，比较清楚地指出了曲线上的点的坐标特征.在处理解析几何问题时，恰当使用参数方程，把许多相关量统一放在一个参数下，就能起到减少变量、简化结构、优化运算的作用.笔者结合自己的教学实践，以详实的例证、深入的分析，谈谈参数方程在解题中的应用.

一、椭圆参数方程在高中数学中的运用

大纲对椭圆的参数方程的要求是理解层次，如果适当地引进一点简单的参数方程知识，可以起到拓宽视野，简化平面解析几何的运算的功效.

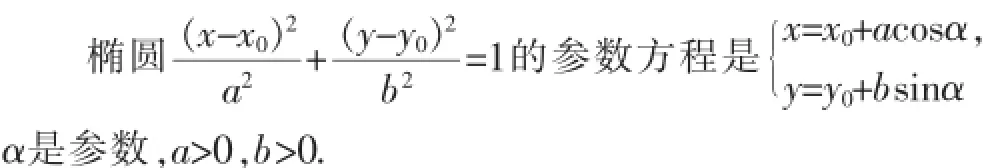
特别地，以点（x0，y0）为圆心，半径是r的椭圆的参数

1.利用参数方程求内接多边形的周长及面积的最值

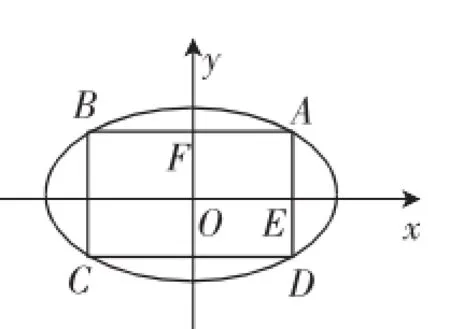
图1

S=4|FA|×|EA|=4acosα·bsinα=2absin2α≤2ab，当且仅

2.利用参数方程求轨迹问题

解：由题意，知B（0，9），设A（12cosα，6sinα），并且设点M（x，y），

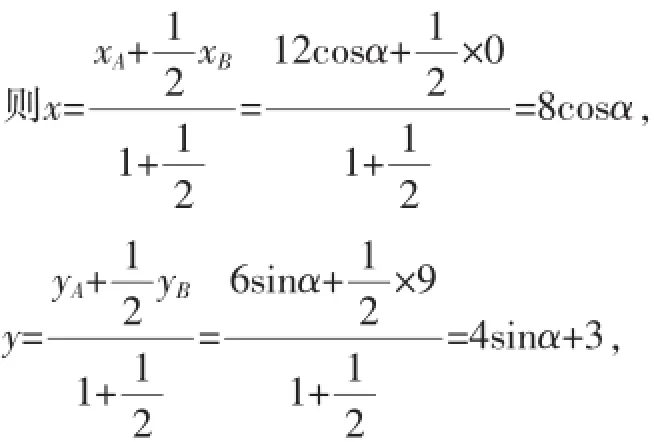
3.利用参数方程求式子的最值

分析：由于研究二元函数x+2y相对困难，因此有必要消元，但由x，y满足的方示出来的x或y，会出现无理式，这对进一步求函数最值依然不够简洁，能否有其他途径把二元函数x+2y转化为一元函数呢？方法是利用椭圆的参数方入x+2y中，即可转化为以θ为变量的一元函数.

分析：若用常规方法求解，涉及A，B两点和线段的中点M的坐标等多个参变量，头绪繁多，需要不断进行思维转移.若引入参数，就可以减少变量个数，简化运算.

解：根据椭圆参数方程，设A（3cosθ，2sinθ），B（3cosφ，2sinφ），P（m，0）.

由线段垂直平分线的性质可知，|PA|2=|PB|2.

于是（m-3cosθ）2+（2sinθ）2=（m-3cosφ）2+（2sinφ）2，

展开整理得5（cos2θ-cos2φ）=6m（cosθ-cosφ）.

又因为AB的垂直平分线与x轴相交，

故AB与y轴不平行，故cosθ≠cosφ，

4.利用参数方程求参数范围问题

例4已知椭

由此可见，在解题时，引入椭圆参数方程，不但可以使解题简化，通俗易懂，思路清晰，而且有利于启发学生思维意识，开拓学生的思维视野，全方位地培养学生探求问题，并能解决问题.

二、直线参数方程在高中数学中的运用

分析：由于该题结论中涉及的PM、PN均可看成直线上动点到定点的距离，因此该题可以设出直线PM、PN的参数方程，使问题迎刃而解.

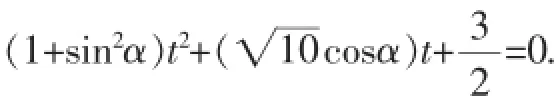
例5过点数），代入曲线方程并整理得设M、N对应的参数分别为t1、t2，而由参数t的几何意义得|PM|=t ，|PN|=t，

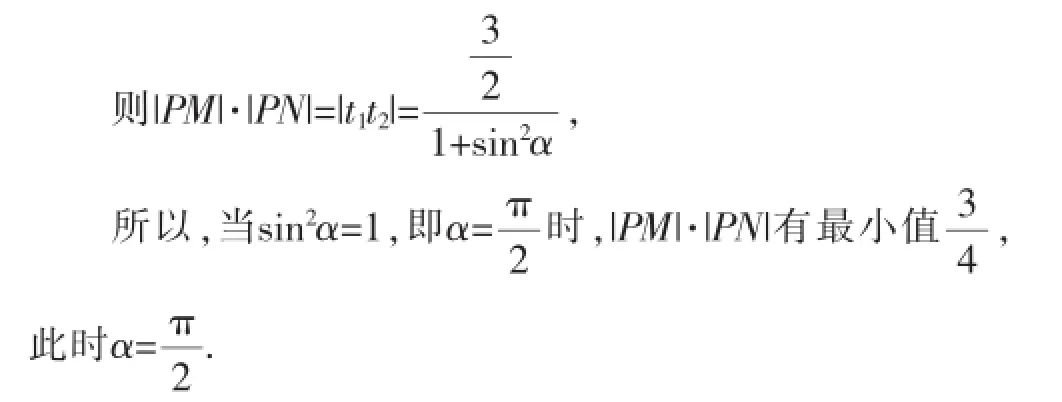
利用直线参数方程中的参数t的几何意义，处理两线段长度的积、和、差以及平方和等问题时有着普通方程无可比拟的优越性，可使求解过程变得简洁易算.

三、圆的参数方程在高中数学中的运用

例6若圆x2+（y-a）2=4与抛物线x2=2y有公共点，求实数a的范围.

由于二次曲线中的变量受到取值范围条件约束，涉及几条二次曲线公共点问题，使用参数方程往往比较严密、简捷.

几条二次曲线有公共点的问题，也可以采用联立方程组的方法来求解，但其中许多关系不是充要条件，很容易出现错误.此题若使用数形结合的方法也是非常困难的.此类问题使用参数方程，将问题转化为三角函数问题，利用三角函数的有界性能使得解答严密而又简捷.

四、综合使用有关参数解决有关问题

例7P（x0，y0）（x0≠±a）是双曲线

（Ⅰ）求双曲线的离心率；

（Ⅱ）过双曲线E的右焦点且斜率为1的直线交双曲线于A，B两点，O为坐标原点，C为双曲线上一点，满足O—→C=λO—→A+O—→B，求λ的值.

本题第一问求出双曲线的离心率从而寻找到字母a、b、c的关系，为第二问求λ的值做铺垫；第二问再利用A、B、C均在双曲线上，建立含有λ的方程式，化简后求出来.关键是利用整体思想设而不求，消去x1、y1、x2、y2、x3、y3等有关相伴变量，以达到化简之目的.

由此可知，参数方程是解决具体数学问题的一个重要方法.利用参数方程或引进参数主要借助于正、余弦和正切，将多个变元统一变量，即所设的参数，使得问题化繁为简、思路清晰、利于计算求值、易于掌握.历年高考都把解析几何作为一个极为重要的知识考查点，参数方法的应用在高考中也极为广泛.G