一道抛物线定直线问题的再探究
2016-05-11郑剑晖
一道抛物线定直线问题的再探究
福建省莆田第五中学(351100)郑剑晖
《数学通讯》2014年第5、6期(上半月)文[1]由2014年《福建省高考“集结号”最后冲刺模拟卷》中的一道压轴题给出了抛物线焦点与准线的关联性质及推广,即结论1、2、3、4,并发现了抛物线另一优美性质,即结论5、6. 读后颇受启发,但觉意犹未尽.本文拟对这些结论进行推广,并进一步探究抛物线在这一相同条件下的另一些优美性质. 先把结论1~6抄录如下:
已知点A、B为抛物线C:y2=2px(p>0)上的两个动点,点A在第一象限,点B在第四象限,直线l1、l2分别过点A、B且与抛物线C相切,点P为直线l1、l2的交点.
结论1 若直线AB过抛物线C的焦点F,则动点P在抛物线C的准线上.
结论2若动点P在抛物线C的准线上,则直线AB过抛物线C的焦点F.
结论3 若直线AB过定点Q(a,0)(a>0),则动点P在定直线x=-a(a>0)上.
结论4若动点P在定直线x=-a(a>0)上, 则直线AB过定点Q(a,0).
结论5若直线AB过抛物线C的焦点F,则以AB为直径的圆过点P.
结论6若以AB为直径的圆过点P,则直线AB过抛物线C的焦点F.
以上结论揭示了抛物线C的焦点与准线、类焦点与类准线的关联性质,下面对以上性质进行推广和再探究.
一、再探究1:探究结论的推广
上述结论1、2分别是结论3、4的特殊情况,而结论3与结论4、结论5与结论6互为逆命题 .能否把结论3、4,结论5、6推广到更一般的情形?
先看结论3、4,若把其中直线AB所过的“定点Q(a,0)”推广为“定点Q(a,b)”,那么动点P是否在某定直线上?
设动点P(x0, y0),则切点弦AB所在直线的方程为y0y=p(x+x0). 若直线AB过定点Q(a,b)(b2<2pa),则有by0=p(a+x0),即p(x0+a)-by0=0.这表明动点P(x0, y0)在定直线p(x+a)-by=0上; 反之,若点P(x0, y0)在定直线p(x+a)-by=0(b2<2pa) (在抛物线外部(不含焦点的区域)的部分)上,则有p(x0+a)-by0=0,即px0=by0-ap.代入直线AB的方程y0y=p(x+x0),得y0y=px+by0-ap,即y0(y-b)=p(x-a).这表明直线AB过定点Q(a,b).由此可把结论3、4推广为:
已知点A、B为抛物线C:y2=2px(p>0)上的两个动点,点A在第一象限,点B在第四象限,直线l1、l2分别过点A、B且与抛物线C相切,点P为直线l1、l2的交点.
结论7直线AB过定点Q(a,b)(b2<2pa),则动点P在定直线p(x+a)-by=0上.
结论8若动点P在定直线p(x+a)-by=0(b2<2pa)上,则直线AB过定点Q(a,b).
特别地,当b=0时,结论7、8分别为结论3、4.
对于结论5、6 ,其中“以AB为直径的圆过点P”,即两切线l1、l2的斜率k1、k2满足k1k2=-1.若把其中直线AB所过的“焦点F”推广为“类焦点Q(a,0)”,那么两切线l1、l2的斜率k1、k2应满足什么条件?
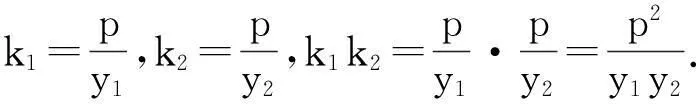
综上,可把结论5、6推广为:
已知点A、B为抛物线C:y2=2px(p>0)上的两个动点,点A在第一象限,点B在第四象限,直线l1、l2分别过点A、B且与抛物线C相切,点P为直线l1、l2的交点.
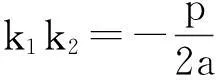
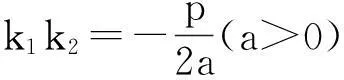
二、再探究2: 探究新结论
在上述结论的条件下,抛物线C还具有哪些优美的性质?经探究,抛物线C还具有如下一些优美的性质:
已知点A、B为抛物线C:y2=2px(p>0)上的两个动点,点A在第一象限,点B在第四象限,直线l1、l2分别过点A、B且与抛物线C相切,点P为直线l1、l2的交点.
结论11若直线AB过抛物线C的焦点F,则分别以PA、PB为直径的圆均过抛物线C的焦点F.
结论12若分别以PA、PB为直径的圆均过抛物线C的焦点F,则直线AB过抛物线C的焦点F.
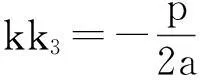
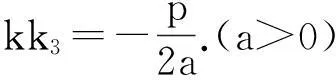
结论15若直线AB过定点Q(a,0)(a>0),且直线l1、PQ、l2的斜率k1、k2、k3均存在,则k1、k3、k2成等差数列,即k1+k2=2k3..
结论16若直线l1、PQ、l2的斜率k1、k3、k2均存在且成等差数列,即k1+k2=2k3.,则直线AB过定点Q(a,0)(a>0).
显然,结论11、12是结论13、14的特殊情况,下面只证明结论13、14、15、16.
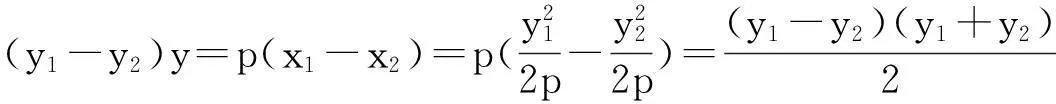
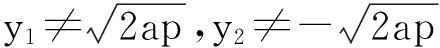
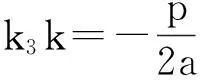
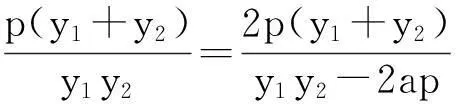
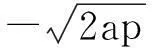
至此,我们完成了对文【1】的结论的推广和再发现.
参考文献
[1]卓文隆.一道抛物线定直线问题的推广[J].数学通讯,2014(5、6)(上半月).
