动中觅静，动静转换——例析妙解旋转类数学问题



动中觅静，动静转换
——例析妙解旋转类数学问题

浙江省温州中学(325014)刘旭飞胡浩鑫

从辩证角度看，动与静是相对存在的，仔细观察题目特点，动中觅静，以静制动，动静转换，不失为处理动态性问题的良策．面对旋转类问题，抓住旋转中的不变量或利用动静转换，常能帮助我们突破思维的屏障、找准切入点、明确解题方向．课堂教学中发现旋转类问题学生都感觉难以下手，本文想结合具体案例谈一谈解决这类问题常见的两种策略．

一、动中觅静，以静制动

自然界的一切事物都在不停的运动着，静止是相对的．反应在数学上就是数量关系和空间形式变换着，而在变中又蕴含着不变的因素，若能抓住这些不变的性质或不变量作为解题的突破口，问题便迎刃而解．

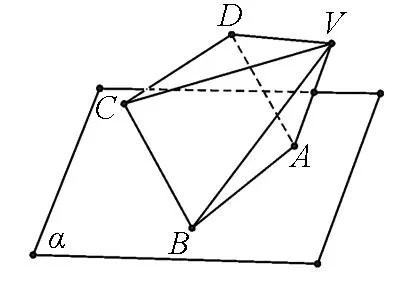
图1

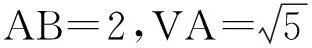
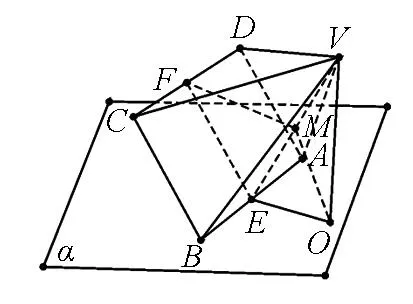
图2

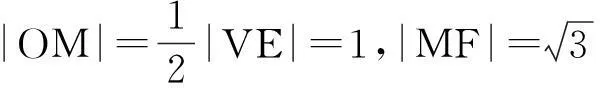
点评：本题难点在于旋转过程中，点O和C都不定，很难找到突破口.方法一从运动中找不变的量入手，动中觅静，以静制动，这是解决这类问题的常用手段.要留心错解：|OC|≤|OM|+|MF|=3，此时等号取不到，因为O,M,F三点不可能不共线.方法二借助向量工具，活用向量分解，把已知向量分解为模或向量之间夹角确定的向量，化动为静，从而达到问题的轻松获解.

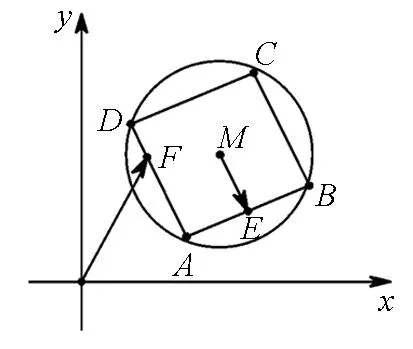
图3

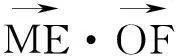
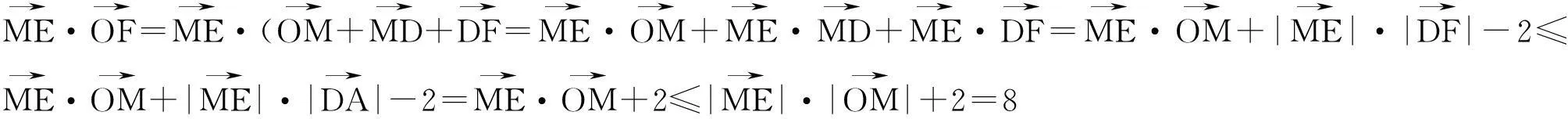
点评：该思路把所求的向量分解转化为模或向量之间夹角确定的向量，以相对确定的向量来表示变化向量，从而减少运算量、思维量，达到化变为不变，化动为静，以静制动的效果，使问题变繁为简.

二、动静转换，另辟蹊径

运动和静止是相对的，运动的A相对于静止的B，也可看成B动A静，利用动静之间的这种相对性来解决动态数学问题常能收到出人意料的效果．

例3(2011浙江省五校联考)将函数y=sinx(0≤x≤2π)的图像绕坐标原点逆时针方向旋转θ(0≤θ≤2π)角，得到曲线C.若对于每一个旋转角θ，曲线C都是一个函数的图像，则满足条件的角θ的范围是( ).

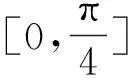
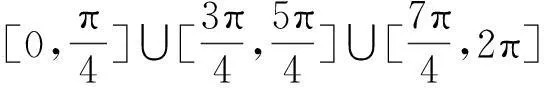
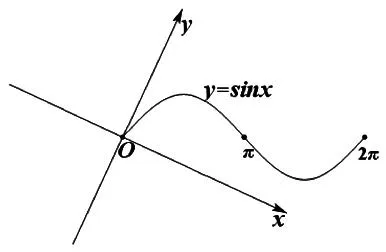
图4

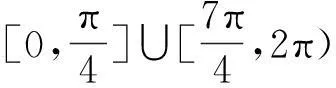
解析：正弦函数图像旋转很难看出它何时还是一个函数的图像，不如来个动静互换，即把正弦函数图像看作不动，如图4，让坐标轴绕坐标原点顺时针转动，只需看和y轴平行的直线是否和y=sinx(0≤x≤2π)的图像只有一个交点即可，易得到选项C．

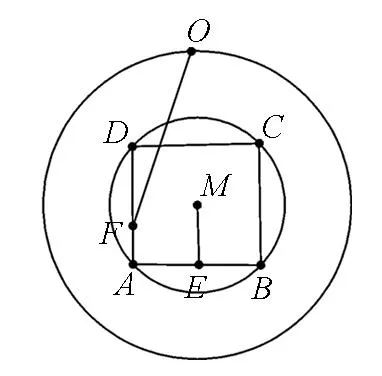
图5

例4同例2．

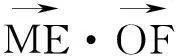
点评：该问题按常规思维去解决会显得复杂甚至束手无策，但换个角度，把多点运动转化为单点运动，脱掉复杂的外衣，使原本问题难度大大降低，真是“山穷水尽疑无路，柳暗花明又一村”．

例5同例1．

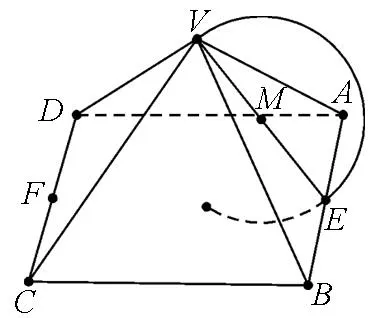
图6

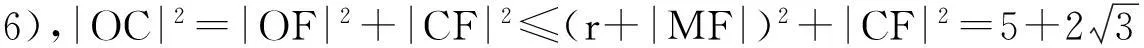
点评：该思路运用运动的相对性，突破常规，反客为主，进行动静转换，体现出思维的灵活性和广阔性，把化归与转化及数形结合的思想运用得淋漓尽致，可谓妙哉！

上述几例能给读者以抛砖引玉的启示，因此教师有意识地培养学生动中觅静、动静转换的策略，能帮助学生发展良好的个性品质，克服思维定势，善于从变换的角度看问题，从而发现问题的本质特征，有效地解决有关问题．