数学史融入高中对数概念教学中的实践与思考*



数学史融入高中对数概念教学中的实践与思考*

江苏省常熟市浒浦高级中学(215512)殷伟康

江苏省常熟市王淦昌中学(215500)唐洁琼

《普通高中数学课程标准》指出数学课堂教学应“努力揭示数学概念、结论发展过程，体会蕴涵在其中的数学方法，追寻数学发展的历史足迹，把数学的学术形态转化成学生容易接受的教育形态.”章建跃先生提出,教师必须十分重视数学概念教学，尤其是数学核心概念的教学.怎样合理、有效地设计、组织教学,有利于学生更好地理解数学概念，这是值得每一位教师思考和研究的课题.事实上，数学概念并非凭空而来.我们所学的数学概念,大都有着各自产生的背景和发展演变的过程，其间凝聚了数学家们的心血和智慧.“对数”是函数这一章节中的核心概念之一，但“对数”是一个比较抽象的概念，因而，学生对对数产生的必要性缺乏正确的认识，在对数概念本质的理解上存在障碍.如何揭开对数概念那“冰冷美丽而又神秘”的面纱，值得每位教师思考.

M.克莱因认为：“课本中的字斟句酌的叙述，未能表现出创造过程中的斗争、挫折，以及在建立一个可观的结构之前，数学家所经历的艰苦漫长的道路.而学生一旦认识到这些，他将不仅获得真知灼见，还将获得顽强地追究他所攻问题的勇气，并且不会因为他自己的工作并非完美无缺而感到颓丧.”因此，笔者从数学文化的角度出发，运用数学史的有效融入方式，结合学情，对教材进行“二次开发”，尝试“重构式”教学方法进行教学，促进学生理解对数概念.

一、创设情境，引出新知

情境某种放射性物质不断变化为其他物质，每经过1年，这种物质剩留的质量是原来的84%．写出这种物质的剩留量关于时间的函数关系式．

设该物质最初的质量是1，则经过x年，该物质的剩留量为y=0.84x．

问题1我们建立这个函数关系式可以实现计算预测的功能，只要知道时间x就可以计算剩留量y．比如，经过了4年，剩留量是多少？

问题2反过来，如果我们知道了该物质的剩留量y，怎么求出所经过的时间x呢？比如经过多少年，剩留量为0.5？

生：0.84x=0.5.(学生感到茫然，不知所措)

师：其实上述问题就是已知底数a和幂值N，求指数b.“已知底数和幂的值求指数”是一个新运算，这是本节课将要研究的问题．

教学意图：通过具体实例说明研究对数的必要性，从指数函数的实际问题入手，即从学生熟悉的指数形式着手，让学生发现“已知底数和幂的值求指数”新问题(解方程)，引发学生产生认知冲突，激发学生学习的兴趣.

二、以史为鉴，追根索源

师：我们首先来看看数学家们是如何来解决这个问题的.

对数的基本思想可以追溯到遥远的古希腊时代，那个时候，阿基米德(Archimedes，公元前287～公元前212年)就已经研究过几个10的连乘积和10的个数之间的关系，用现代的表达形式来看，就是研究了这样两个数列：

110102103104105106……0123456……

他发现它们之间有某种对应关系，但是阿基米德虽然发现了规律，却没有把这项工作继续下去，失去了对数破土而出的机会．

15、16世纪的欧洲，航海和贸易的迅速发展，极大地推动了天文学和三角学的进步.特别是地理探险需要更为准确的天文知识，为了确定行星的位置或制作天文数表，往往要花上几天甚至几个月的时间进行计算.对计算速度和准确性的要求与日俱增，人们希望将乘、除、乘方、开方归纳为简单的加、减、乘、除来实现.

15世纪，法国数学家许凯(N.Chuquet, 1445～1488)在两个数列中也发现了类似的对应规律.他在其著作《算学三部》中给出了双数列之间的对应关系：

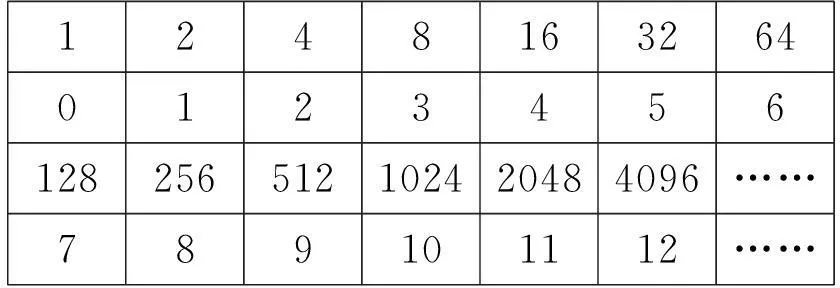
12481632640123456128256512102420484096……789101112……

上一列数之间的乘、除运算结果对应于下一列数之间的加、减运算结果，如4×32=128，对应于2+5=7.16世纪，德国数学家斯蒂菲尔(M.Stifel, 1487～1567)针对双数列更明确地提出了上一列数的乘、除、乘方和开方四种运算法则.还有其他很多数学家也发现了这样的规律，但是由于种种原因，特别是分数指数还没有得到认识，所以他们也没有发明对数.

我们已经学习了分数指数幂，比这些古时候的大数学家们掌握了更丰富的数学知识，我们是不是一起来发明对数呢？

请学生观察以上的两组数，研究阿基米德、斯蒂菲尔等数学家发现了怎样的规律呢？组织学生进行分组讨论，教师适当引导，要求结合指数运算法则.

得出结论：下面一列数的加减运算结果与上面一列数的乘除运算结果有一种对应关系.

师：能否用一个指数的运算法则来表述这个关系？

生：同底数幂相乘，底数不变，指数相加.

如果M=ac,N=ab，那么M·N=ac·ab=ab+c.

上述第二组数据中，第一行表示2的对应幂，第二行表示2的指数，那么，如果我们要计算第一行中两个数的乘积，就可以通过第二行中对应数字的加和减来实现．比如，计算16×64的值，就可以先查询第二行的对应数字：16对应4，64对应6，然后再把第二行中的对应数字加起来4+6=10，第二行中的10对应第一行中的1024，所以有16×64=1024．

也就是说如果我们有类似这样一张表格，就可以通过指数的加减运算来得到幂的积或商.那在具体实施的过程中，我们最好能把指数表示出来.也就是说如果N可以用ab来表示，那么b可以用N表示吗？

教学意图：提供对数知识历史背景和原始问题，增强真实感，引发学生进行探究，追溯数学家发现对数的过程，通过观察分析表格中双数列对应关系，使学生深刻认识到对数对简化运算的重大作用和引进对数的必要性.同时，通过丰富的情景和动人的数学家的历史故事，激发学生的求知欲和创造欲.

三、以史促思，建构概念

后来，英国数学家纳皮尔(J.Napier, 1550～1617)受到上述表格的启发，发现了可以利用这个规律来简便运算的有效工具，于1614年出版《奇妙的对数定理说明书》，这标志着对数的诞生.为了这一划时代意义的发明，纳皮尔整整花费了二十多年时间！他把b称为N的“对数”，今天，我们依然沿用这个称呼，把b称为以a为底N的对数.17世纪，笛卡儿(R.Descartes, 1596～1650)发明了幂的记号，指数概念才应运而生．直到17世纪末，才有人认识到对数可以定义为幂指数．之后，欧拉(L.Euler, 1707～1783)深刻揭示了指数与对数之间的密切联系，并创用了logaN这一记号．这样就有了对数的定义：若ab=N(a>0,a≠1)，则把数b称为以a为底N的对数，记作b=logaN，其中a叫做对数的底数，N叫做真数，读作以a为底N的对数.

思考1将下列指数式写成对数式：

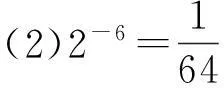
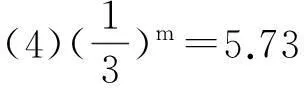
思考2将下列对数式写成指数式：

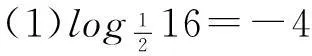
(3)log100.01=-2；(4)loge10=2.303.

注意：①指数式与对数式的关系：ab=N⟺b=logaN (参考指数中底数a的取值范围，强调其中a>0且a≠1，b∈R,N>0)，简单的说求以a为底的对数logaN，就是求a的多少次方等于N.

②概念的进一步理解：指数式与对数式的关系及相应各数的名称排列如下：

式子名称abN指数式ab=N底数指数幂值对数式logaN=b底数对数真数

③a>0时，N=ab>0，所以，负数和零没有对数.

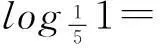
注意④有关性质：loga1= ；logaa= .

教学意图：引导学生在指数式与对数式之间进行互化的过程中，进一步认识对数概念的本质，加深对对数概念的理解，掌握其互化方法.从中让学生感受转化与化归思想方法，学会用联系的观点分析问题和处理问题.

四、以史为镜，深化理解

为了使纳皮尔发明的对数可以更方便地被人们使用，对数历史上的另一位重要人物英国数学家布里格斯(Briggs，Henry,1561～1630)和纳皮尔决定把10作为对数的底.纳皮尔去世后，布里格斯又对纳皮尔的对数进行了改进，他把10进行了54次的开平方后，得到了一个略大于1的数，并取10作为对数的底，造出了常用对数表.比如思考2中的(3)，底数为10，这样的以10为底的对数就称为常用对数，简记作lgN.也就是说(3)可以写成lg0.01=-2.

师：对常用对数和自然对数感兴趣的同学，老师向大家推荐两本课外读物《不可思议的e》和《漫话e》，从中你一定会获得更多的知识.

师：同学们现在能否解决问题2呢？

生：x=log0.840.5≈3.975，即经过大约4年剩留量为0.5.

教学意图：引导学生了解常用对数和自然对数的来历及其应用价值，可以促进学生对对数概念的认识，体会数学和生活的联系.引导学生阅读有关对数的数学史，感悟对数的发明与发展历史及其价值是数学文化的体现，提升学生的数学素养.

五、以史启真，诱发再探

师：拉普拉斯曾经说过：“对数的发现，以其节省劳力而延长了天文学者的生命.”伽利略宣称“给我时间、空间和对数，我可以创造出一个宇宙来.”由此可见，对数在天文学和自然科学中有重要作用.恩格斯把对数的发明和解析几何的创造、微积分的建立称为17世纪数学的三大成就和“最重要的数学方法”.

生：我们了解了对数的诞生过程，学习了对数的概念，以及指数式、对数式之间的互化．

生：指数式、对数式之间的互化中体现了转化思想.

师：同学们畅所欲言的讨论，既梳理了指数、对数等相关知识的内容，又寻味了对数发展史的各个阶段所凝聚的思想、智慧与精神.按照研究数与函数的方法，接下来研究什么呢？

生：对数的运算规律(性质)和对数函数概念及其性质.

师：很好！今天我们认识了对数，感受到了数学家们思考问题的奇妙历程和智慧，也感受到了数学发展推动人类认识世界的巨大力量，并且经历了数学文化的熏陶.希望大家课后通过练习，进一步巩固、理解和掌握对数的概念，明天我们将继续来研究对数的一些运算性质，进一步学习这个新的认识世界的工具！

教学意图：课堂小结意在画龙点睛，让学生对所学的知识作简单的回顾，了解对数的实际应用价值，体验其中蕴含的数学思想方法，并引导学生运用类比的方法，猜想对“对数”进一步研究的方向，诱发学生产生再探究欲望.

六、以史定教，凸现重构

要真正实现数学史有效地融入数学概念教学中，不仅需要教师注重挖掘数学知识点背后的历史，深入理解数学史的知识意义和方法意义，而且需要教师注重结合教学实际和学生的认知水平、数学基本活动经验，对数学史料进行有效地选择、加工，运用发生教学法，采用顺应式、重构式等有效的融入方式，将数学史中与所学的对数概念相关思想方法融入到新知识引入中，创设以数学史料为背景的问题链，引导学生进行自主探究，让学生经历“寻找解决问题的方法”，引入新的运算(对数运算、引入新的数学符号表征数学对象的需要)的过程，再现数学历史原貌，展示对数概念的发生、发展过程，让学生在获得知识的过程中，体验其中蕴含的思想方法，促进学生去感悟和建构对数概念，理解对数概念所蕴含的本质特征，增强学习数学的信心，培养理性思考和执著的探求精神.本节课运用了大量有关对数的数学史料，选取学生能够理解的且有一定教学价值的部分按历史顺序“去支强干”进行重组，并从历史发生原理出发，对有关对数知识历史发展过程中的关键步骤与环节，进行了再加工，进而对知识的历史进行重构，使其适合学生认知和课堂教学，并设计一系列由易至难、环环相扣的问题.通过“重构”历史上对数概念的发生、发展过程的方式，引导学生自己建构新概念，从而在真正意义上理解对数概念的内涵和本质.

“数学文化的历史，以其独特的思想体系，保留并记录了人类在特定社会的形式和特定历史阶段文化发展的状态.”因而，在数学概念教学中，教师要对所教数学概念相关的素材进行历史挖掘，让学生感受数学文化的渊源.也就是说，教师需要对所教主题的数学历史知识有深刻的理解，才能对知识的历史进行重构，以史为鉴，善于把“现成的知识”还原为“现实的问题”，创设富有数学历史背景的问题链，让学生在问题探究和解决中经历数学知识的发生、发展过程，并通过追寻大师的足迹、仰望大师的风采，汲取人类文明中的无穷智慧和坚韧不拔的探究精神，经历数学文化的熏陶.而且要揭示数学概念中所蕴含的数学思想方法，引导学生感悟和领会其实质.如果仅一知半解、只见树木不见森林，数学概念的重构就难以达到“自然而然”的教学效果，数学史料反而成了累赘．其次，同一个数学家的历史轶事，不同的讲述方式会产生不同的教学效果，教师会讲“故事”，也是一种教学实力.再次，教师在运用数学史料时必须要把握尺度，或张或弛，或详或略，一切均以满足课堂教学的需求和适合学生的认知水平为准则，一方面，不能将数学课堂异化为“故事课”，另一方面，也不应只是简单用数学家的历史轶事点缀一下课堂，匆匆带过，而应该要舍得花时间，给予学生倾听、领悟和思考的时空.在体验对数概念的生成过程中，引导学生积极思考，学会有效思考.进而能提出自己的观点和思路，逐步养成问题意识、探究意识和创新意识，提升数学文化修养.

参考文献

[1]钟萍,汪晓勤. 对数概念：从历史到课堂[J]．中学数学月刊, 2015(5)：50-53．

[2]金惠萍,王芳.HPM视角下的对数概念教学 [J]．教育研究与评论, 2014(9)：28-34．

*本文系江苏省教育科学“十二五”重点资助课题：构建数学文化课堂的教学实践研究(课题批准号B-a/2013/02/069)研究成果之一.