数学探究式教学要把握“时机”*

●金惠忠　(金华市第六中学　浙江金华　321000)



数学探究式教学要把握“时机”*

●金惠忠(金华市第六中学浙江金华321000)

摘要:与传统教学模式相比，探究式教学模式在激发学生的学习兴趣、体现学生在学习过程中的主体地位等方面有着不可比拟的优势．但似乎也因此陷入一个怪圈，只重探究不重课堂效果．事实上，在探究式教学过程中“时机”的把握至关重要．

关键词:数学;探究式教学;时机

基于“把课堂还给学生”的美好出发点，探究式教学在各地普遍展开．但似乎也因此陷入一个怪圈，教师往往为了探究而探究，不讲究课堂教学的真实效果．笔者认为，在数学课堂教学中，探究教学的时机把握非常重要，不可一概而论．笔者结合教学实践谈谈在探究式教学过程中“时机”的把握．

1　探究式教学前置——在预习中引入探究

传统预习是指上课前对即将要学习的内容进行阅读，预先了解课本或导学案内容［1］．这种直接看文本的做法，笔者认为有一些缺陷:1)降低了学生学习的兴趣．由于事先已经阅读了文本，学生对即将学习的新知识和相关数学结论已经了解，这样在上课时，对教师精心设计的问题情境、知识和结论的探索过程就会失去兴趣．2)降低了学生的思维深度和广度．由于学生失去兴趣，从而课上自主探究过程的参与程度就弱化了，学生只记住了相关结论，而在探究过程中需要培养的数学思维方法就得不到培养．

笔者认为将探究式教学前置，抓住预习这个时机引入探究，可以较好地解决传统预习带来的缺陷．这种预习就是在课前教师精心设计一个问题［2］，引导学生进行自主探究或者小组合作探究，进而引出新知识，达到预习的效果．具体操作模式如下:课前展示问题→课前学生探究→检查预习报告→课上汇报展示→整理、归纳新知→知识应用．现以“二倍角公式”教学中将探究式教学前置操作过程为例进行说明．

1．1课前展示问题

案例1如图1，四边形ABCD是半径为R的圆O的内接矩形，试探究四边形ABCD面积的最大值．

1．2检查、批阅预习报告

在课前，笔者检查了学生自主探究的情况，全班85%的学生都进行了认真地探究，70%的学生结论正确，50%的学生采用了不少于一种方法探究，具有代表性的方法有4 种:

图1

方法1设点A到BD的距离为h，则

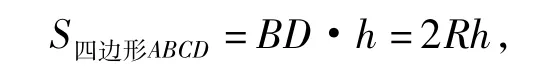
由圆的相关几何知识可知，hmax=R，故Smax=2R2．

方法2设AD=x，AB=y，则

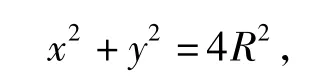
由恒成立不等式可知

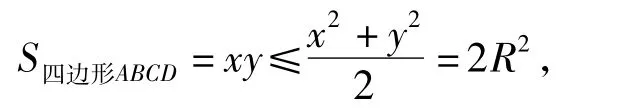
方法3设∠AOD=θ，θ∈(0，π)，则点A到BD的距离为Rsinθ，从而

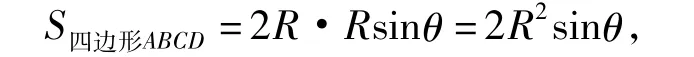
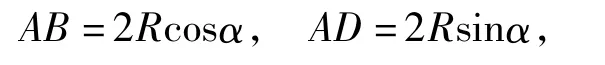
故

1．3课堂展示汇报

笔者根据学生自主探究的情况，安排几位学生将有代表性的解法进行展示与汇报，并进行有针对性的点评．

1．4归纳、总结，发展新知

1)在课堂上，引导学生关注方法3和方法4，方法3中的参数θ和方法4中的参数α之间有什么联系?由此你发现了什么新的结论?此时大多数学生发现这样一个结论:sin2α=2sinαcosα．

2)进一步探究:这个公式是否具有一般性，α可以取任意实数吗?

3)再进一步探究:二倍角的余弦、正切又是怎样的呢?从而顺利引导学生学习新知——二倍角公式．

奥苏伯尔曾经说过:“如果我必须把整个教育心理学归纳为一个原则的话，我会这样说，影响学习的一个最重要因素是学习者已经了解了什么”［3］．学习者了解的知识将构成新知识的先行组织者，这种先行组织者将有助于学生将新知识与已有认知结构中相关的部分联系起来，从而构建出新知识．探究式教学前置，在预习中引入探究，通过课前解决一个问题，激活学生已有认知结构中的先行组织者，为学习新知识作充足的准备．

将探究由课堂上现场操作移至课前，从而达到预习效果，这样既培养了学生自主探究的能力，又节约了课堂时间，从而提高课堂效益．

2　探究式教学伺机而动——在核心内容生成处引入探究

新授课涉及的多是数学概念、定理、公式及性质等，对这些数学内容的教学，部分教师认为过程不重要，会用就可以了，基础较差的学生甚至只要死记硬背就行．笔者认为对于基础不好的学生，更要讲清它们的来龙去脉，因为数学结论的证明中就蕴涵了一些重要的数学思想，为使学生的思维活动有效展开，对新授课上的核心内容生成时展开探究是很有必要的［4］，现以“点到直线的距离公式推导”的教学片断为例．

案例2求点P(3，3)到直线l:2x+y－4=0的距离．

在探究式课堂教学中，学生产生了如下几种方法．

方法1过点P作直线l的垂线，垂足为Q，通过直线l与直线PQ得到交点Q的坐标，利用两点间距离公式可计算PQ．

方法2如图2，过点P作x轴的平行线PR交直线l于点R，作y轴的平行线PS交直线l于点S．在△PRS中，由PQ，即可得到PQ．

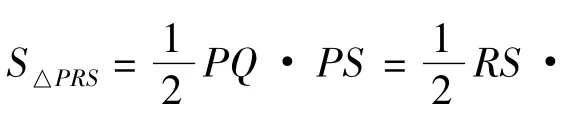
图2

方法3想到“点P到直线l的距离PQ的本质，就是点P到直线l上任意一点Q'之间距离的最小值”．因此可设Q'(x0，y0)为直线l上任意一点，则

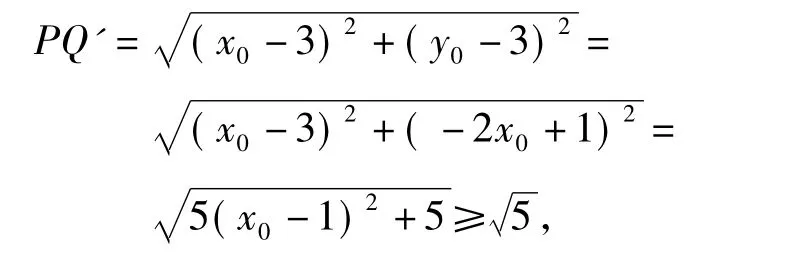
方法1是将点线距离转化为两点间的距离，方法2是将“斜距离”转化为“横线段、竖线段”，方法1和方法2都体现了数学的转化思想．方法3是将几何问题转化为代数问题，将问题转化为求函数最值问题，体现了解析几何的思想方法．

有了上述过程的体验和铺垫，学生的认识由特殊向一般转化，进而求点P(x0，y0)到直线Ax+ By+C=0的距离就水到渠成．新授课时，对涉及到数学概念、定理、公式及性质等数学核心内容的生成部分，利用课堂中的一部分时间进行局部探究，使学生认清知识的来龙去脉，重建学生的知识体系，将探究式教学和教师讲授教学有机结合，将获得课堂效益最大化．

3　探究式教学以点带面——在学生易错点引入探究

数学解题中的错误与数学学习随处相伴，只要有数学学习，就会出错．在习题课中，基于学生错误的典型性，以及学生对问题解决的强烈愿望，在小组讨论探究的基础上，由教师进行点评，提炼通性通法．现以“数列的定义和性质习题课”的教学片断为例进行说明．

案例3已知数列{an}的通项公式为an= n2+λn，且{an}为递增数列，则实数λ的取值范围是()．

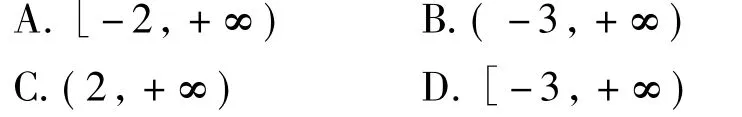
通过查阅、批改学生的作业了解到学生在本题求解时，有3种典型方法:

学生方法1设函数f(x)=x2+λx，显然f(x)在上是增函数．由{an}为递增数列可知，从而λ≥－2．故选A．

学生方法2设函数f(x)=x2+λx，由{an}为递增数列可知，f'(x)=2x+λ≥0在x∈N*上恒成立，只需f'(1)=2+λ≥0，得λ≥－2．故选A．

学生方法3由于{an}为递增数列，故an＜an+1在n∈N*上恒成立，即

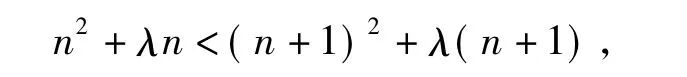
化简得2n+1+λ＞0在n∈N*上恒成立，因此λ＞－(2n+1)max，即λ＞－3．故选B．

在习题课上教师抛出这样3种学生解题时的典型思路，学生就开始小声议论，因为大家认为这3种方法似乎都显得无懈可击．那为何又会出现不同的结果呢?思维的火花已经点燃，探究的气氛已经生成．这时引导学生分组合作、讨论探究，由于问题是学生引起的，学生解决问题的意愿较为强烈，讨论的气氛异常热烈．

最后小组代表给出意见:事实上，要使数列{an}为递增数列，只要求满足不等式a1＜a2＜a3＜…＜an＜…．结合二次函数的图像，an=n2+λn为一系列离散的点，那么只需其对称轴在直线的左边，从而，得λ＞－3．

在给予充分肯定之后，教师作适当点评:方法1和方法2的错误在笔者考虑到数列是特殊的函数，而没有考虑这2者之间的区别，忽视了数列的离散性特征．由于数列{an}的定义域为正整数集(或子集)，故其图像是一系列离散点．

为了解决学生在易错易混淆处出现的问题，在学生探究的过程中，充分暴露思维上的错误和瑕疵，及时点拨，给他们充分思考的空间和机会［5］．教师在整个过程中更多承担的是引导者和启发者的角色，而课堂的主动权已交给了学生．基于这样一些“美丽的错误”，在习题课的教学中适时展开探究显得尤为重要，从学生的视角出发，让学生体验探究的乐趣，从而给课堂带来了传统习题课所没有的生命力．

探究式教学的优势是传统教学方式所不可比拟的，但它并不是所有内容都适用．这就要求教师首先要分析教学内容是否需要引入探究教学，假如通过探究教学确实有助于学生理解数学的本质，那么教师就要精心设计，把握好引入探究教学的时机，从而将数学课堂成为学生主动从事数学活动、构建自己有效数学理解的场所．同时要做好探究式教学和其他教学形式的整合，以期真正提高数学课堂的质量，焕发数学课堂新的生命力．

参考文献

［1］蔡国琦．高中数学课前预习优化策略探究［J］．语数外学习(数学教育)，2012(10):4．

［2］燕学敏．问题意识:数学课堂有效教学的关键［J］．数学通报，2010(3):20-23．

［3］奥苏伯尔．教育心理学——认知观点［M］．北京:人民教育出版社，1994．

［4］方志平．高中数学探究式教学问题创设的探究［J］．高中数学教学参考:上旬，2013(12): 12-14．

［5］王开林．解题教学活动应注重培养学生的数学思维品质［J］．数学教学研究，2015(12): 17-21．

作者简介:金惠忠(1981－)，男，浙江金华人，中学一级教师，研究方向:数学教育．

修订日期:*收文日期:2015-12-31;2016-01-20．

中图分类号:O12

文献标识码:A

文章编号:1003－6407(2016)04-07-03