说题，助推数学教师专业发展*

●冯　涛　(北仑中学　浙江宁波　315800)



说题，助推数学教师专业发展*

●冯涛(北仑中学浙江宁波315800)

摘要:著名数学教育家波利亚说过:中学数学教学的核心任务是解题，解题是中学数学中最有用的精华．本文结合笔者在2015年浙江省宁波市优质课评比中的说题案例，旨在阐明中学数学教师在专业成长中离不开解题研究，说题是助推教师成长的一种重要形式．说题不只是说，它包括了题目解法的探究、题目的推广与引申、题目的深层次背景及其教育价值的挖掘．

关键词:说题;专业成长;教学价值

2015年浙江省宁波市高中数学优质课评比在余姚中学举行，来自各市区县的代表参加了这次比赛．此次比赛分为上课展示和说题2个环节，说题环节的比赛在第一天下午展开，其规则大致和浙江省第2次说题比赛保持一致，即参赛教师从现场抽取题目，在单独的教室准备30分钟，然后在15分钟时间内向专家评委解读该题的解法、背景、引申、拓展以及教学价值．笔者有幸参加了这次比赛，并荣获市一等奖．算上这次说题比赛的经历，笔者已经参加了3次类似的专业比赛，对笔者在数学教育专业上的成长起到了助推器的作用，以下笔者结合说题经历谈谈自己的体会．

1　说题引领教师深入研究解题

波利亚说过:中学数学教学的核心任务是解题．他又说:解题是中学数学中最有用的精华．每一位刚刚入行的数学教师都会被要求多解题，多研究高考题、竞赛题，保持对解题旺盛的兴趣和精力，并以此为契机打好坚实的解题功底．教师的解题与学生的解题有很大的区别，教师不仅要研究解题的结果，更加要关注数学本质以及内在思维方法和数学结构，而学生往往只是关注解题的结果．如果教师的解题停留在学生的层次，那么久而久之，教师的解题水平乃至兴趣都会下降，专业发展基本趋于停滞．因此说题这样一种教研活动实际上是一种助推教师个人专业发展的有效形式，它推动参与其中的每一位教师在研究状态下进行日常的解题，将解题从一种简单自发的工作任务转变为自觉的学科研究行为．

此次说题比赛的第1个环节是说题目的解法，笔者抽到的题目是2015年上海市数学高考理科试题第14题．这是一道平面向量与平面几何相结合的小题，总体难度并不大，笔者将所探求的主要解法整理如下:

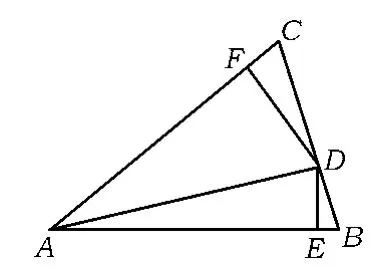
图1

(2015年上海市数学高考理科试题第14题)

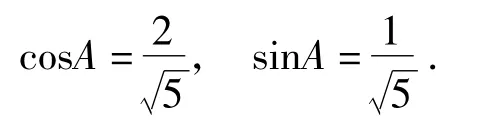
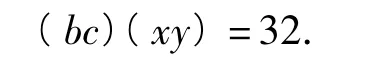
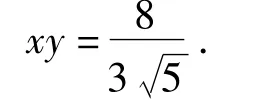
注意到∠EDF+∠A=π，因此从而

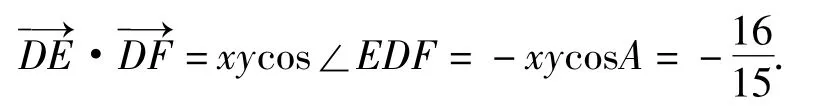
解法2(消元法)

在解法1中，若没有将2个面积等式整体相乘处理，则不妨考虑消元．由，知

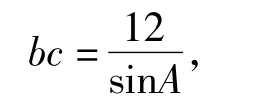
从而

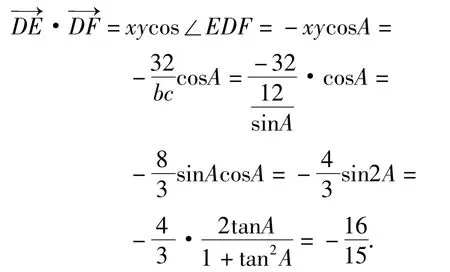
解法3在解法2的基础上进一步改进消元法，以x为主元处理．如图2，注意到点D 分BC恰为1∶2，故可作CG⊥AB于点G，则

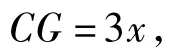
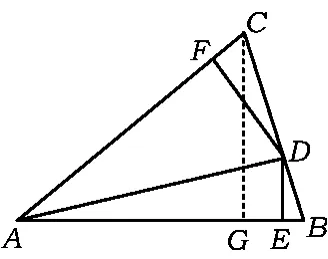
图2

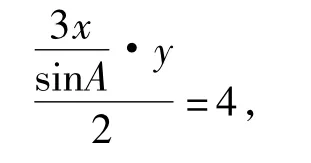
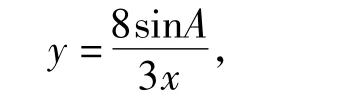
即，于是

故

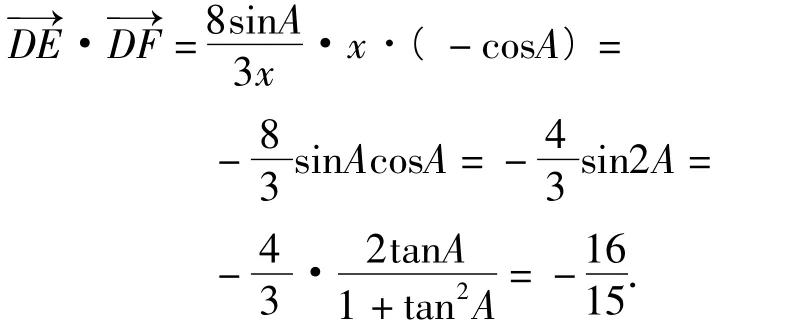
解法4将面积条件换个角度看，以∠CAD=

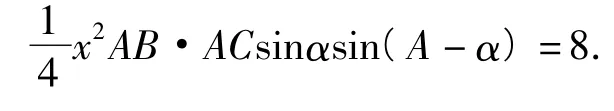
从而

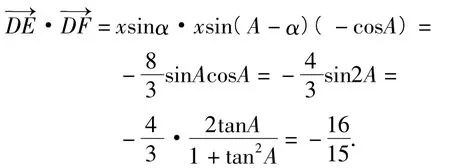
解法5以A为原点、AB为x轴、过点A且与AB垂直的直线为y轴建立坐标系．设点C的坐标为

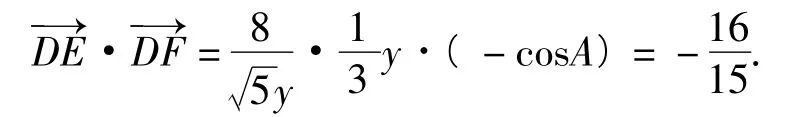
解法6利用向量投影的意义解决．只需要利用四点共圆，从而∠A与∠EDF的补角相等．延长ED，作FM⊥ED于点M，改进解法5，向量的投影为

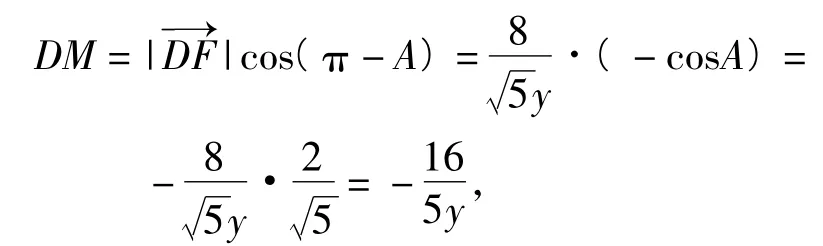
根据数量积的几何意义可知

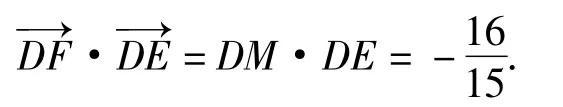
由于该题并不难，无论哪种解法都需要将已知条件中的面积关系与所要求解的数量积联系起来，以上这些不同的解法实际上是相通的，形式变化，而本质不变．若继续探究，此题还有更多的解法，这种在解法上的求异思维、发散思维对教师提高解题能力和养成好的思维习惯大有裨益．

2　说题引领教师深化思维，挖掘数学本质

孟子曰:“贤者以其昭昭，使人昭昭．”意思是:要让别人明白一件事情，自己首先要弄明白这件事情．因此，对于说题而言，探究一道题目的多种解法只是完成了说题的一个阶段工作，如果教师在教学中也只是向学生展示了若干解法而不知引导学生升华思维，探究数学本质，那么好比入宝山而空返，这就需要教师进行解题后的追本溯源，深入剖析，高屋建瓴地把握解题规律，并有意识地将这样的研究方法固化，一方面引领自身的专业发展，同时也引领学生优化思考方式，学会数学解题，最终达到培养思维能力的目的．

此次说题的另一重要环节就是说题目的引申与拓展．对这道题目而言，笔者经过深入探究得到了一系列一般性的结论，具体计算过程可以参考解法1，以下不再赘述．

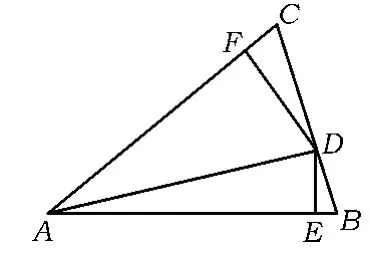
图3

1)将题目条件一般化．

如图3，在锐角△ABC中，tanA=μ，D为边BC上的点，△ABD与△ACD的面积分别为s，λs(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

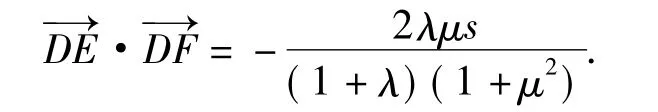
2)将大前提改为钝角三角形，其他条件相应也进行一般化．

如图4，在钝角△ABC中，∠A，∠B，∠C之一为钝角，tanA=μ，D为边BC上的点，△ABD与△ACD的面积分别为s，λs(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

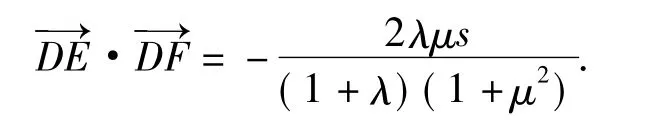
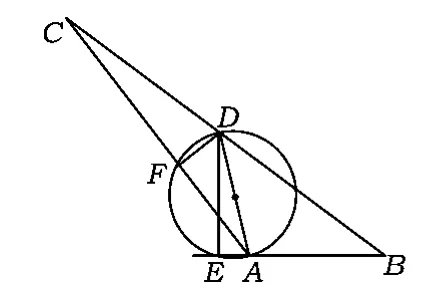
图4

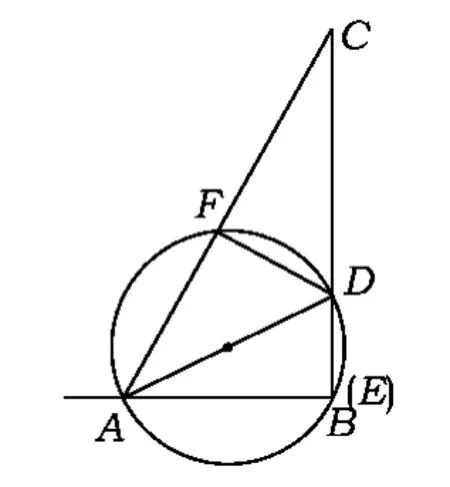
图5

3)将大前提改为直角三角形，其他条件相应也进行一般化．

①如图5，在Rt△ABC中，∠B，∠C之一为直角，tanA=μ，D为边BC上的点，△ABD与△ACD的面积分别为s，λs(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

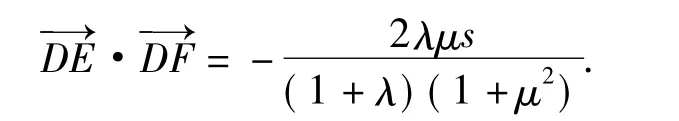
②在Rt△ABC中，∠A为直角(tanA无意义)，D为边BC上的点，△ABD与△ACD的面积分别为s，λs(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥ AC于点F，则

说明以上引申1)～3)主要改变了大前提——三角形的形状，除了当∠A为直角时结论退化为0外，其余情形结论不变．这表明此题设置为锐角三角形或许只是为了降低考生对发现∠A与∠EDF互补这一隐含关系的难度，否则当三角形为钝角三角形时，需要借助四点共圆中同弧所对圆周角相等来处理此题．另外，结论中的可以利用万能公式化为sin2A，这样结论显得更加简洁，只是考虑到条件是tanA=μ，读者可以自行推导．

4)将题目的求解目标变成最值．

在锐角△ABC中，总面积设为定值s，tanA=μ，D为边BC上的点，△ABD与△ACD的面积之比为λ(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

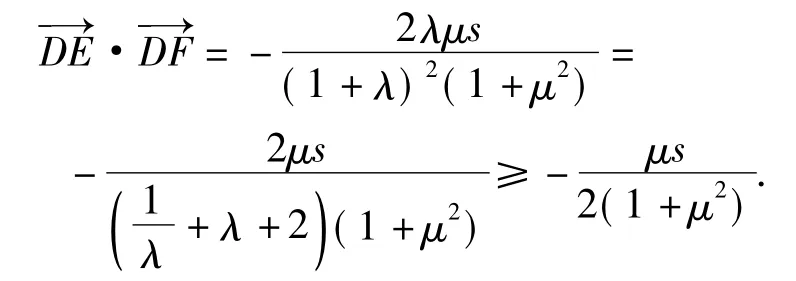
5)将三角形改为钝角三角形，求解目标变成最值．

在钝角△ABC中，∠B，∠C为钝角，总面积为定值s，tanA=μ，D为边BC上的点，△ABD与△ACD的面积之比为λ(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

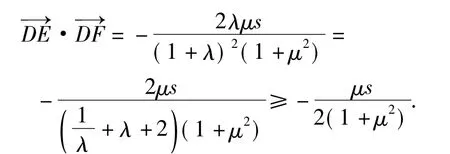
6)将三角形改为钝角三角形，求解目标变成最值．

在钝角△ABC中，∠A为钝角，总面积为定值s，tanA=μ，D为边BC上的点，△ABD与△ACD的面积之比为λ(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

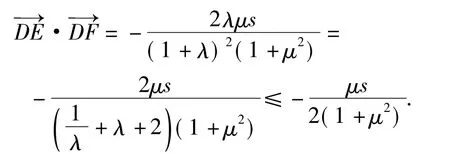
说明以上引申5)和6)的区别在于:当∠A为钝角时，目标有最大值;当∠A不为钝角，∠B或∠C为钝角时，目标有最小值，并且都是在当且仅当点D在中点时达到相应的最值．如果把三角形改为直角三角形，当∠A为直角时没有最值，只有定值0;当∠B，∠C为直角时，∠A为锐角，此时目标有最小值

由于比赛时间和自身认识结构的局限性，以上的一些引申与拓展，也可能尚未看到问题的本质，但通过对题目多角度的思考，教师的研究方法值得肯定，对所研究题目的结构也会逐渐清晰起来．

3　说题引领教师钻研学科教学

在教师的专业发展中，教师的数学专业知识对于教学至关重要，但是并非具备了充足的数学知识就能成为一名好教师，还需要具有针对特定数学内容的教学知识，需要懂得教育学、心理学，清晰的语言表达能力，需要将数学的知识形态转化为教学形态，最终服务于学生对数学的理解．

此次说题的第3个环节是说教学价值，只需要教师思考该问题在高中数学知识结构中的价值以及如何把这个问题讲清楚，讲透彻．

从知识上说，此题考查了解三角形面积知识、三角函数恒等变换知识、向量数量积知识、圆的知识、基本不等式知识等．

从方法上说，它涉及了消元法、主元法、方程法、整体代换法、坐标法等．

从思想上说，它应用了数形结合思想、主元思想、方程思想、化归思想，在引申中用到了一般化思想和函数思想等．

在课堂教学中可以尝试让学生先自行解答，教师从旁引领鼓励学生发表看法，并总结学生的解法，小结解题的知识、方法、思想，甚至可以鼓励学生变题和编题．

例2如图6，在锐角△ABC中，总面积为定值s，tanA=μ，D为边BC上的点，△ABD与△ACD的面积之比为λ(其中λ＞0)．过点D作DE∥AC，DF∥AB，则

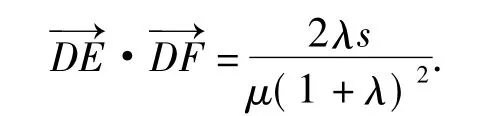
学生把原先2个垂直条件改变为平行，那么2个对角的互补关系变成了更为直接的相等关系，在其他条件不变的情形下，解决这个问题的数量积显得更加顺利，并且这是一个比较常见的向量数量积问题，还有学生认为原题命题者是在平行的基础上，为了增加难度，而将平行改为了垂直．学生的参与将一堂传统以教师讲授为主的课转化为了以学生探究为主的、师生合作的探究性课，效果截然不同．

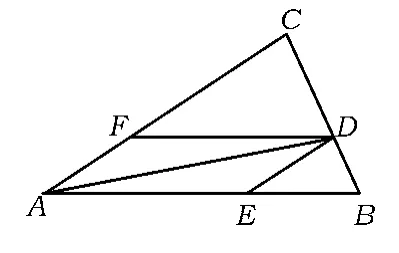
图6

图7

4　说题引领教师反思创新

一位教师在专业发展过程中，最终是成为一名专家型的教师还是普通的教书匠，关键在于反思，比如这道题目除了以上的引申和拓展，似乎总是离问题本源尚存在距离，也就是说此题的深层数学背景是什么呢?

此次说题还有一个环节就是说背景，这需要教师透过现象看本质，这道题目条件中已知一个内角和三角形面积以及该内角的对边上一个分点就能计算数量积，这说明数量积与面积有莫大的关联，经过笔者探究发现，以锐角三角形为例得到:

例3在锐角△ABC中，tanA=μ，D为边BC上的点，△ABD与△ACD的面积分别为s，λs(其中λ＞0)．过点D作DE⊥AB于点E，DF⊥AC于点F，则

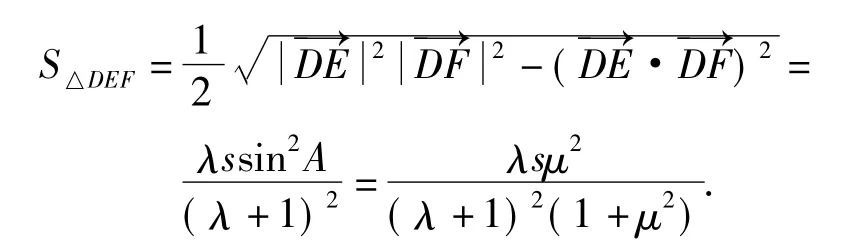
思考2此题另一个可能的背景是，此题可以联想到向量积的模就是以2个向量所在边构造的平行四边形的面积，那么经探究可得与存在如下关系:

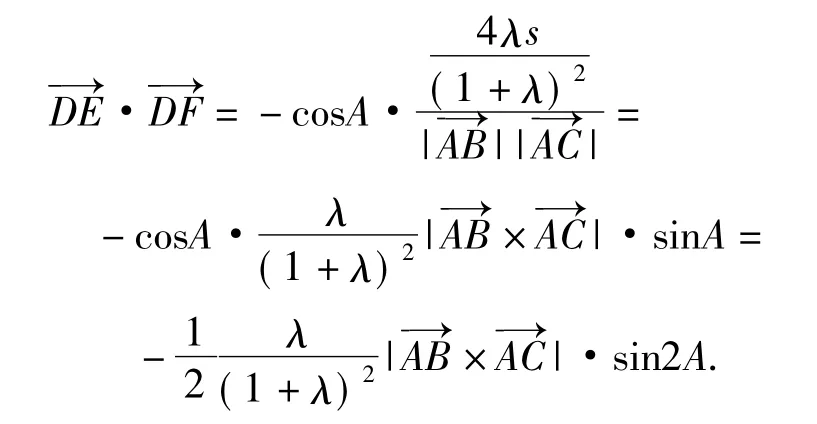
诚然，以上的反思和引申拓展离真正的创新尚存在差距，甚至并未将数学的本质看透，但是它至少引领我们明白解决一个题目并不是万事大吉，它助推了教师养成解题后反思的习惯．只要这样的研究状态持之以恒，我们的进步是巨大的，那么距离真正意义上的创新也就不远了．

数学教师的专业发展是一个不断学习和积累数学学科知识的过程;是一个数学技能不断形成和能力不断提高的过程;是一个数学素养不断形成和提升的过程．而说题恰好提供了一个十分契合的模式，有力地助推了数学教师的专业成长，除此之外，专业的发展还需要对数学教育理论不断学习，对课堂教学进行深刻反思，对教学行为进行及时地调整．

作者简介:冯涛(1979－)，男，浙江宁波人，中学一级教师，研究方向:数学教育．

修订日期:*收文日期:2015-11-08;2015-12-11．

中图分类号:O12

文献标识码:A

文章编号:1003－6407(2016)04-03-04