基于时段解耦的含特殊负荷的配电网动态无功优化*

欧阳森　杨家豪　安晓华　陈欣晖

(华南理工大学 电力学院∥广东省绿色能源技术重点实验室， 广东 广州 510640)



基于时段解耦的含特殊负荷的配电网动态无功优化*

欧阳森杨家豪安晓华陈欣晖

(华南理工大学 电力学院∥广东省绿色能源技术重点实验室， 广东 广州 510640)

摘要：针对特殊负荷的扩大化趋势导致配电网中潮流分布不确定、电压波动范围增大、无功电压调控困难的问题，提出一种含特殊负荷的配电网动态无功优化方法.基于随机潮流计算对含特殊负荷的配电网潮流不确定性进行描述；针对离散控制设备动作次数约束造成动态无功优化问题的时空强耦合性，提出一种时段解耦策略来实现原问题的解耦并将其转化为逐时段连续优化决策；基于电压概率分布信息及设备调节能力分别设计了电压质量和设备动作罚函数，优化目标充分计及网损、电压概率分布以及设备调节能力的共同作用，根据优化进程中的控制变量及状态变量信息实现配电网无功电压的趋优控制.最终，以IEEE33节点配电网进行实例分析，验证了文中所提方法的有效性.

关键词：配电网；动态无功优化；时段解耦；特殊负荷；随机潮流；多种群遗传算法

配电网是电力系统的重要组成部分，是输电网和用户之间的重要中间环节.随着新能源和可再生能源发电技术的发展，分布式电源(DG)在配电网中的渗透率逐渐升高[1]，加之现代工业中具有强波动性、冲击性的新型负荷的出现[2]，这些特殊负荷的接入会对配电网造成一系列影响.传统辐射形配电网的潮流方向由于DG的渗入而转变为非单向潮流，而且DG出力大小的随机性以及新型工业负荷的波动性、冲击性将直接影响配电网中的潮流特性，使得原本在各时段内认为较为确定的潮流分布亦呈现较强的不确定性，同时潮流分布的不确定性还将引起各节点电压波动范围的增大.上述情况都增加了配电网的无功调度与无功电压控制的难度[3]，因此考虑含特殊负荷的配电网动态无功优化对提高配电网经济效益、降低运行风险、保证电压质量具有现实意义.

此外，由于受制造技术和设备寿命的限制，各控制设备都不允许频繁地投切，在时间尺度上将导致各时段的无功电压控制策略存在相互影响与制约.而从空间尺度上看，各控制设备的运行状态非独立，共同对配电网的潮流及电压分布起作用，因此动态无功优化问题具有复杂的时空强耦合性[4- 10].而考虑含特殊负荷的配电网动态无功优化则需要重点解决以下两方面问题：①对特殊负荷的不确定性进行合理的描述，以求全面反映特殊负荷接入后配电网的运行情况，并获得高置信度下的趋优解；②针对离散控制设备动作次数约束造成动态无功优化问题的时空强耦合性进行适当的处理以降低求解难度.

文中拟建立含特殊负荷的配电网动态无功优化模型，运用概率模型描述特殊负荷的不确定性，并基于随机潮流求解状态变量的概率分布以全面反映特殊负荷接入后配电网的运行状态；针对离散控制设备动作次数约束造成动态无功优化问题的时空强耦合性，提出一种时段解耦策略实现原问题的解耦并转化为逐时段连续优化；设计了考虑电压质量与设备调节能力的罚函数，优化目标计及网损、电压概率分布以及设备调节能力的共同作用，充分利用优化进程中的控制变量及状态变量信息对配电网无功电压进行趋优控制.最终文中以IEEE33节点配电网进行实例分析，对文中所提出方法的有效性进行验证.

1特殊负荷概率模型及随机潮流

配电网中各类型的典型特殊负荷如表1所示.

表1　配电网中典型特殊负荷

由表1可知，波动、冲击负荷多为新型工业负荷，典型波动负荷(如电弧炉等冶炼负荷)、冲击负荷(如轧钢机等)受生产工艺的影响，其工作过程往往伴随着功率波动与冲击，此类特殊负荷在工作状态下负荷功率受运行工况决定，难以用单一运行状态值进行描述.而对于DG,由于目前风速、光强的预测误差较大，且预测提前的时间越长其误差越大，在现有技术水平下，仅通过改进预测方法进一步提高其预测的准确性存在困难，若在无功优化过程中对于含特殊负荷的配电网仅根据节点注入功率预测值的时间序列进行优化，其优化结果的工程实用价值较低[11]，因此有必要将各时段的特殊负荷注入功率以概率分布形式进行不确定性描述.

文献[12- 13]运用场景分析法对风电进行场景划分，可以从一定程度上对DG出力进行概率描述，但划分场景过于粗糙且当多种服从不同场景概率的特殊负荷同时接入时会引发求解场景组合的“维数灾”.文献[14]引入随机潮流(PLF)求解含DG的配电网无功优化，由于随机潮流理论能够有效地解决潮流计算中的不确定性问题，因此可以成为求解含特殊负荷的配电网潮流的有效工具，而对特殊负荷建立概率模型是随机潮流计算的基础.

常规负荷的概率模型通常视负荷基准值为均值，适当描述随机波动的方差，用正态分布描述其统计特性.负荷的有功和无功功率的概率密度函数可分别描述如下：

(1)

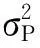
区别于常规负荷，特殊负荷接入配电网呈现更强的不确定性.相比传统发电方式，DG具有随机性大、波动性强、出力不可控等特点，目前较为成熟的DG形式以风力发电及光伏发电为典型代表.应用最广泛的DG出力建模即基于风速的Weibull分布及光照强度的Beta分布近似获得风力发电出力及光伏发电出力的概率分布模型[15- 16].亦可采取根据地区实际统计获得DG出力的离散概率分布的方式建立分布式电源的出力概率分布模型.波动负荷、冲击负荷的概率建模则基于实测数据进行统计，将负荷有功及无功功率实测数据以区间形式进行测算，将负荷功率的概率分布以相应概率的离散数据进行表示，从而形成特殊负荷概率模型.

以某典型冲击负荷实测数据为例，当统计区间宽度取为Δd时，第i个区间内数据点个数为ni，总数据点个数为N，则各区间的概率密度为

(3)

当各区间的负荷功率以中值表示时，其相应概率值则可按下式转换：

(4)

经过上述处理获得如图1所示的典型冲击负荷实测数据转换后的概率模型.

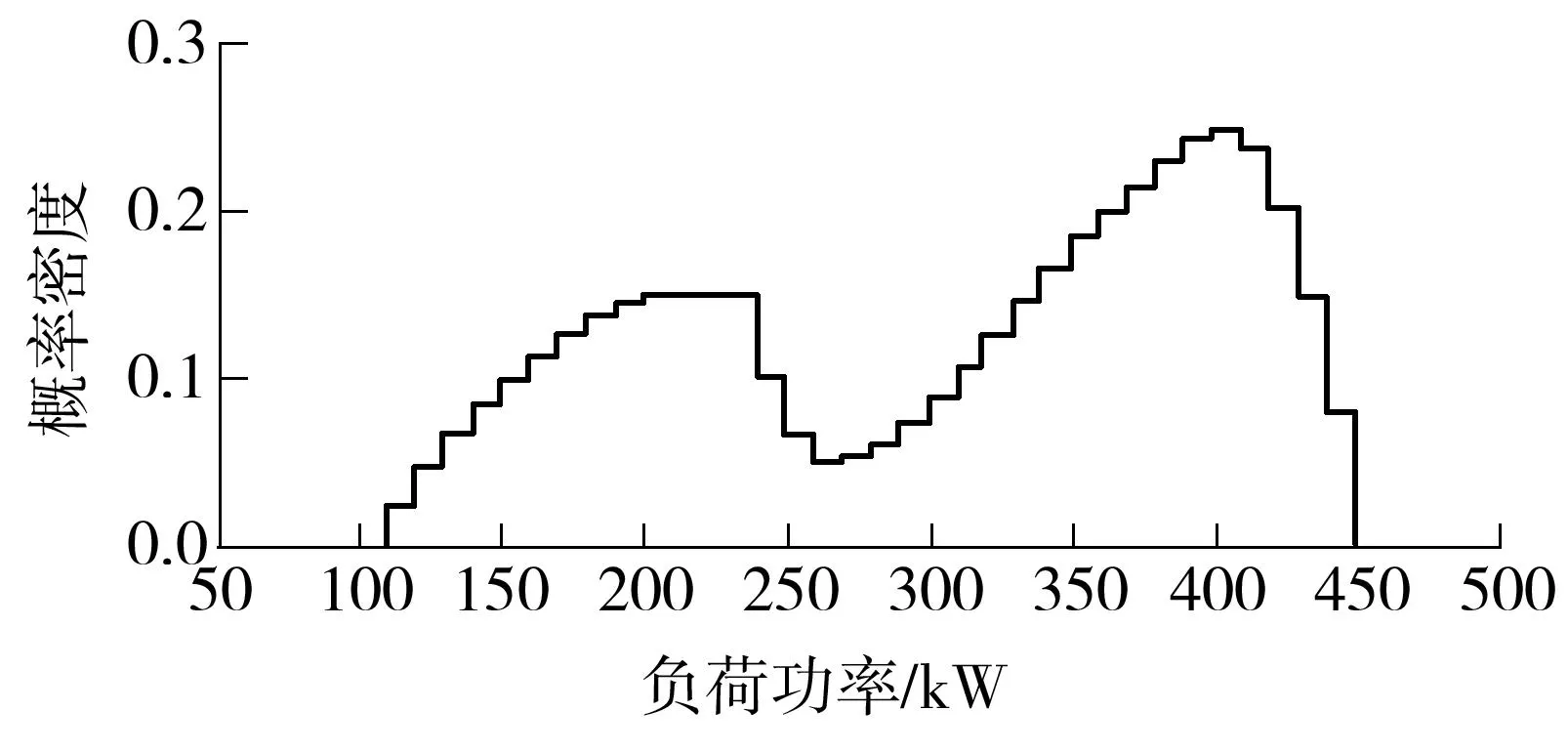
图1　典型冲击负荷实测数据转换后的概率模型

Fig.1Probabilitymodelofmeasuredtypicalshockloadsafterconversion

特殊负荷的接入会造成系统潮流不确定，随机潮流理论能够有效地解决潮流计算中的不确定性问题，对含特殊负荷的配电网运用随机潮流计算可以合理地描述其随机性与不确定性对潮流及电压概率分布的影响[15- 18].

求解随机潮流的方法主要分为模拟法及解析法：模拟法主要是指蒙特卡罗模拟法(Monte Carlo Method)[18]，其根据不确定量的概率模型产生一定规模的样本，分别对每个样本进行潮流计算，再统计得到随机分布规律，其最大问题是计算量过大、周期过长.解析法则是在基于对研究问题近似线性化的数学假设下根据不确定量数值特征，用逼近的方法获得随机潮流解的近似解析表达式.其中关键问题在于需要进行复杂的卷积计算，而利用概率特征求出半不变量简化随机变量间的卷积计算，进而利用级数展开求得概率分布可以减少解析法的计算复杂性，提高随机潮流计算的效率.

由于在优化过程中需要进行大量的随机潮流计算，并且文中所建立的优化模型中存在概率约束，为加快计算速度以及获取状态变量的概率分布信息，文中将采用基于半不变量及Gram-Charlier级数展开的随机潮流计算方法[16].

2动态无功优化求解算法

针对离散控制设备动作次数约束造成动态无功优化问题的时空强耦合性，文中对传统动态无功优化数学模型进行解耦，简化了求解过程.

2.1动态无功优化模型

配电网动态无功优化问题是指在网络结构参数及未来一天配电网各节点负荷有功和无功变化曲线给定的情况下，通过调节并联电容器组的投入组数及有载调压变压器分接头档位，在满足各种运行约束的条件下使配电网全天24个时段的网损之和最小.传统动态无功优化的数学模型如下：

(5)

式中，Ploss(u,x)为单一时段的网损值，F为全天24个时段的网损累加和即总目标函数，g(u,x)为系统潮流约束，其中u和x分别为控制变量及状态变量，umax、umin、xmax、xmin分别为控制变量及状态变量对应的上下限，Nu为设备动作次数，Nmax为动作次数限值.

2.2动态无功优化解耦策略分析

动态无功优化是非线性的多时空多变量的复杂优化问题，文献[4]建立非线性混合整数动态无功优化模型并运用原对偶内点法求解，但对24个时段同时寻优，加上动作次数的约束，增加了求解的难度，且当约束条件苛刻时，算法的收敛性得不到保证.文献[5- 6]将负荷曲线分段，但没有明确分段方法，且需要对动作时刻进行预判.

为了简化动态无功优化的求解，部分文献设计了相应的解耦策略.文献[7]采取将负荷曲线分段后进行合并的策略，保证分段数不超过动作次数的约束，尽管可限制动作次数但其往往局限于配电网各节点负荷服从一致的变化规律以及要求控制设备同时动作；文献[8]设计设备的动作表来进行解耦，以静态无功优化效果来分配设备的动作权限，但动态调整后的设备动作可能存在失配问题；文献[9]从启发式算法的编码方式计及动作次数的约束，消除了不可行解但待求解量包含各设备的动作时刻与动作量，没能根据负荷实际变化情况对设备动作时刻进行确定，寻优过程较为盲目且难以保证搜索到全局最优解，且由于编码方式要求设备全天动作次数必须恰好达到限制次数增加了额外的约束；文献[10]将空间变量乘以时段数以得到全面描述时空的控制变量，对动作次数的约束是通过统计每个空间断面的控制变量取值的变化次数进行校核，将带来编码过长、求解难度加大的问题.

目前所采取的解耦策略各有偏重，总体而言多存在以下局限性：①要求配电网各节点的负荷变化规律一致，可能与实际情况不符；②要求各控制设备同时动作，对系统的冲击较大，不利于实时调度，且各控制设备之间不存在配合；③将各设备的动作时间作为待求解量，增加求解维度致使搜索范围指数化增大，在寻优过程中无法提供指导寻优方向的策略，只能依赖随机搜索不利于求得最优或趋优解.

文中针对上述问题提出一种时段解耦策略，将原问题解耦并转化为逐时段连续优化决策，且各时段特殊负荷可根据实际代入不同的注入功率概率分布进行计算.其核心思想为反复通过上一时段的最优解去指导本时段的寻优方向，充分利用优化进程中的控制变量及状态变量信息对配电网无功电压进行趋优控制.由于在每一优化的时段均在目标函数中引入考虑关于相对于该时段的剩余时段内各控制设备的剩余调节能力的罚函数，将离散设备动作次数从约束条件中转移，使其以罚函数形式存在，有效降低了计算复杂度.在该罚函数的作用下将对设备不必要的动作进行限制，有效控制设备动作次数.

2.3时段解耦后的优化模型

解耦后的各时段的无功优化数学模型如下：

(6)

式中， f为单一时段的目标函数，Ploss(u,x)为单一时段的网损值，V(x)与K(u)分别为电压质量罚函数以及设备动作罚函数，并且将状态变量约束改写为概率约束，置信度Prob文中取0.95.

由于优化目标中结合所设计的罚函数充分计及网损期望、电压概率分布信息以及设备调节能力的共同作用，能够兼顾配电网网损及电压质量的控制.通过对罚函数控制参数的合理设计，可以合理地权衡冲突目标之间取舍从而进行决策.

2.3.1电压质量罚函数

在无功电压控制中应力求配电网各节点电压尽量稳定于标幺值附近，因此文中所设计的电压质量罚函数将充分利用随机潮流求解得的状态变量信息即电压概率分布，从而对电压质量进行控制，电压质量罚函数具体形式如下式所示：

(7)

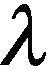
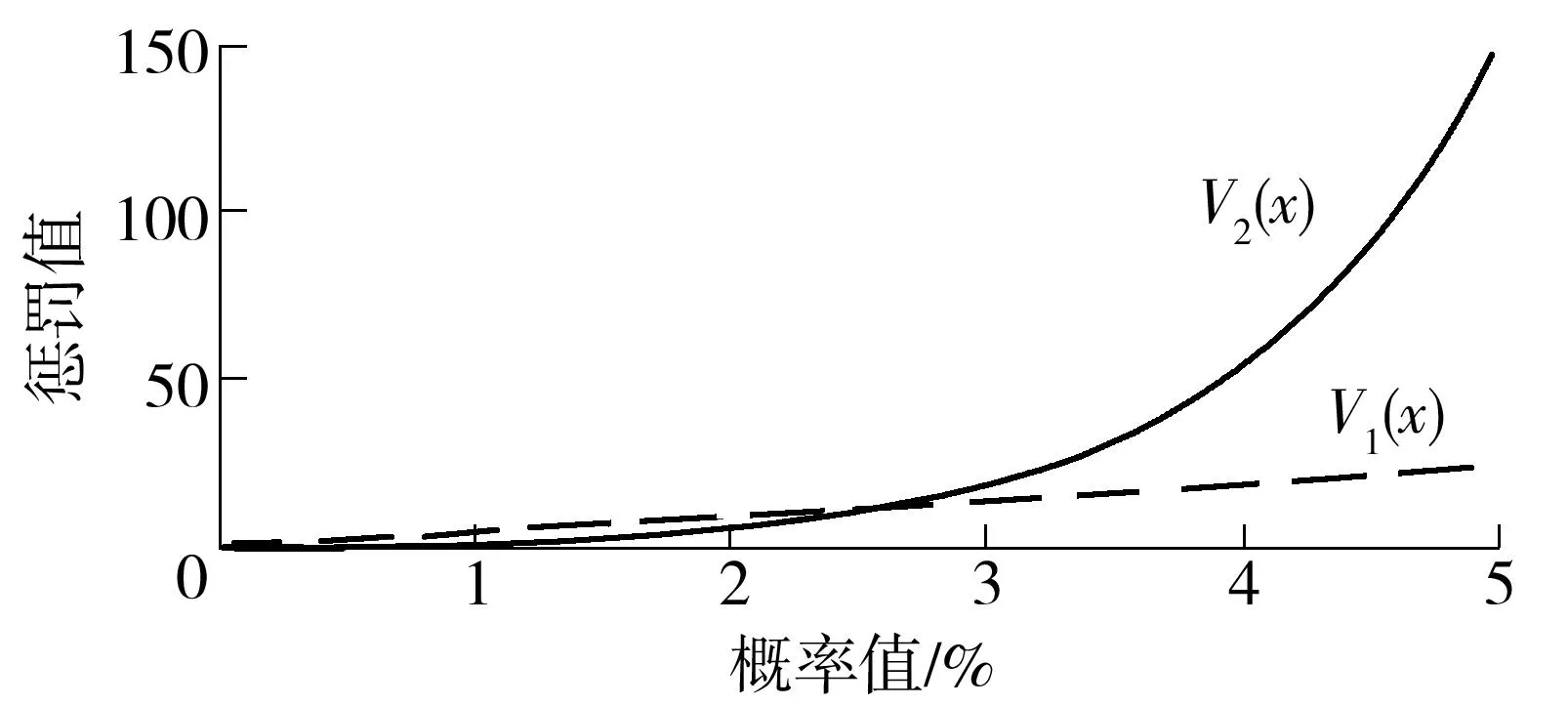
图2　电压质量罚函数曲线

2.3.2设备动作罚函数

基于优化进程中控制变量的信息建立设备动作罚函数，对于设备的动作次数约束文中将其划分为两个层面：其一是设备的日动作次数严格上限值Nmax，仅对解的可行性起校验作用；其二是设备的日动作次数期望上限值Nexmax，仅对优化进程中罚函数的惩罚程度进行调节.设备动作罚函数设计为如下形式：

K(u)=αexp(-βNr/tr)×(u⊕u0)

(8)

其中：α、β为罚函数参数，u0为上一时段的控制变量状态，Nr为当前时段的设备剩余调节能力(相对于日动作次数期望上限值Nexmax而言)，tr为当日待优化的剩余时段数，Nr/tr表征了剩余单位时段的设备可调节能力，该值越小对应罚值越大.α、β的选取建议参考以下原则：当剩余调节能力低于20%时，应使惩罚值达到平均网损水平的8%～15%，当剩余调节能力大于50%时，应使惩罚值不多于平均网损水平的4%.

各控制设备在各时段的罚函数仅由自身的剩余调节能力决定，因此在同一时段内不同控制设备的动作罚函数值可能存在差异.在这种机制下，对任意时段的优化过程中，可促使剩余调节能力大的设备在一定程度上获得较大的动作权限，反之可限制已消耗较多调节能力的设备的动作.

2.4求解算法

文中的算法流程图如图3所示.

2.4.1多种群遗传算法

遗传算法(GA)[19]可以有效地解决离散整数优化问题，因此在传统的无功优化中已得到了广泛的应用.文中采取多种群遗传算法(MPGA)[20]进行优化求解，不同种群赋予不同的交叉概率与变异概率通过移民操作来增强寻优性能，同时采取精英保留策略以防止最优个体遭到破坏.算法结构示意图如图4所示.

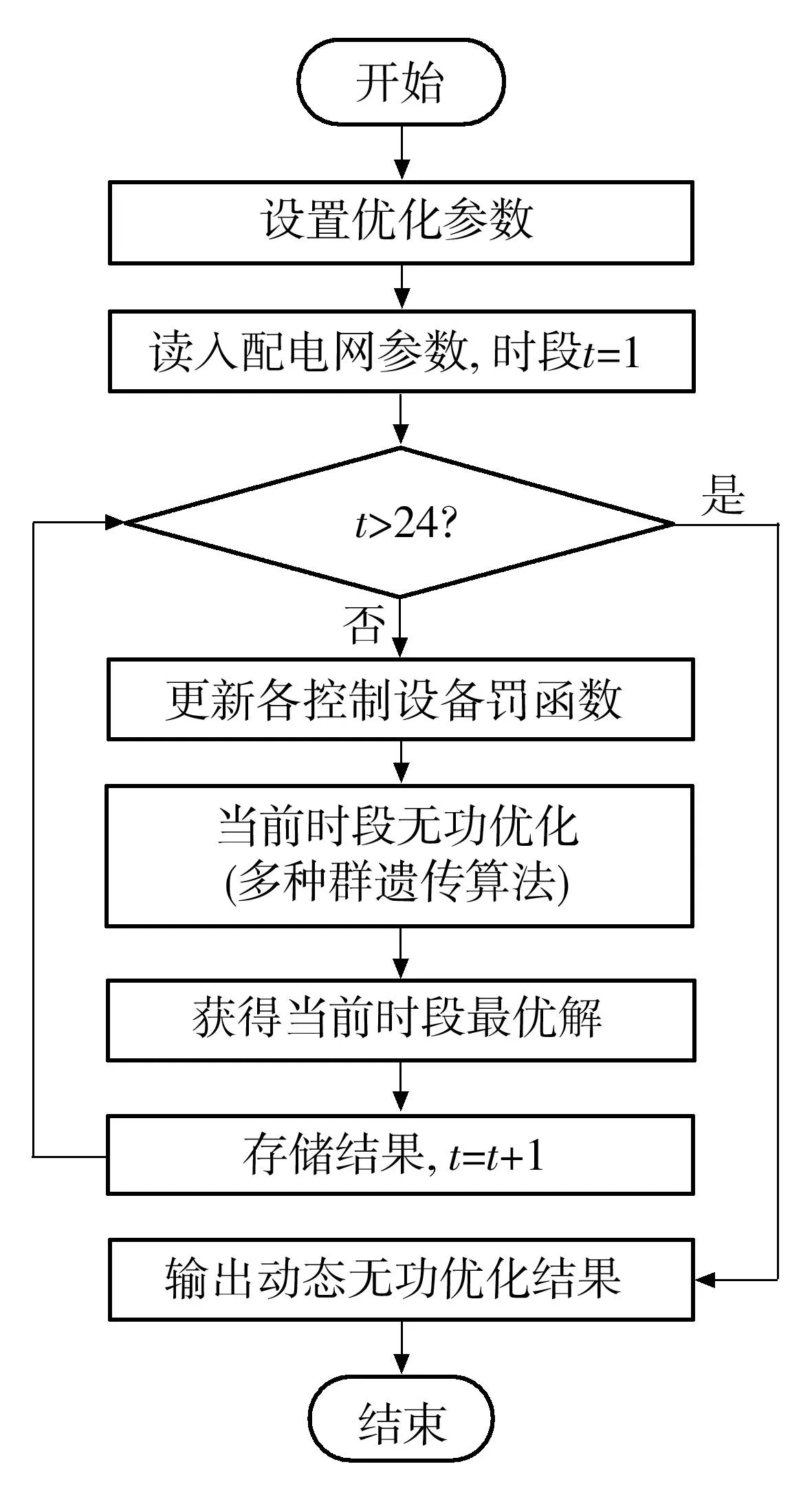
图3　算法流程图

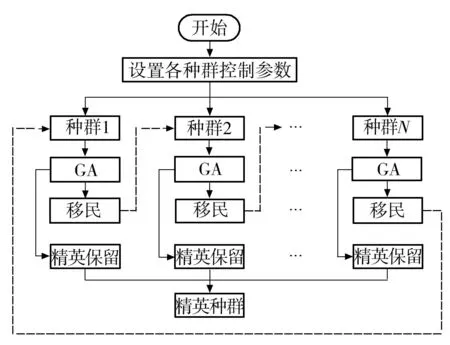
图4　MPGA算法结构图

2.4.2初始种群产生策略

初始种群产生策略根据动态无功优化问题进行了相应调整，常规GA一般采取随机产生初始种群的方法，由于动态无功优化各时段的控制设备状态力求在上一时段的基础上不做过大的改变，因此在产生初始种群后附加轮盘赌操作，每个个体逐位进行轮盘赌操作，在一定的概率判断下保持某位为上一时段的状态，可以有效使当前时段种群从上一时段最优个体附近开始搜索本时段最优解，对寻优方向起一定指导作用.此外为保持种群多样性，应间隔一定代数减少占统治地位的个体(同一个体在种群中占比过大)，候补种群亦采用同样的产生策略.

2.4.3解的修正环节设计

在优化过程中引入修正环节，修正环节流程如图5所示.

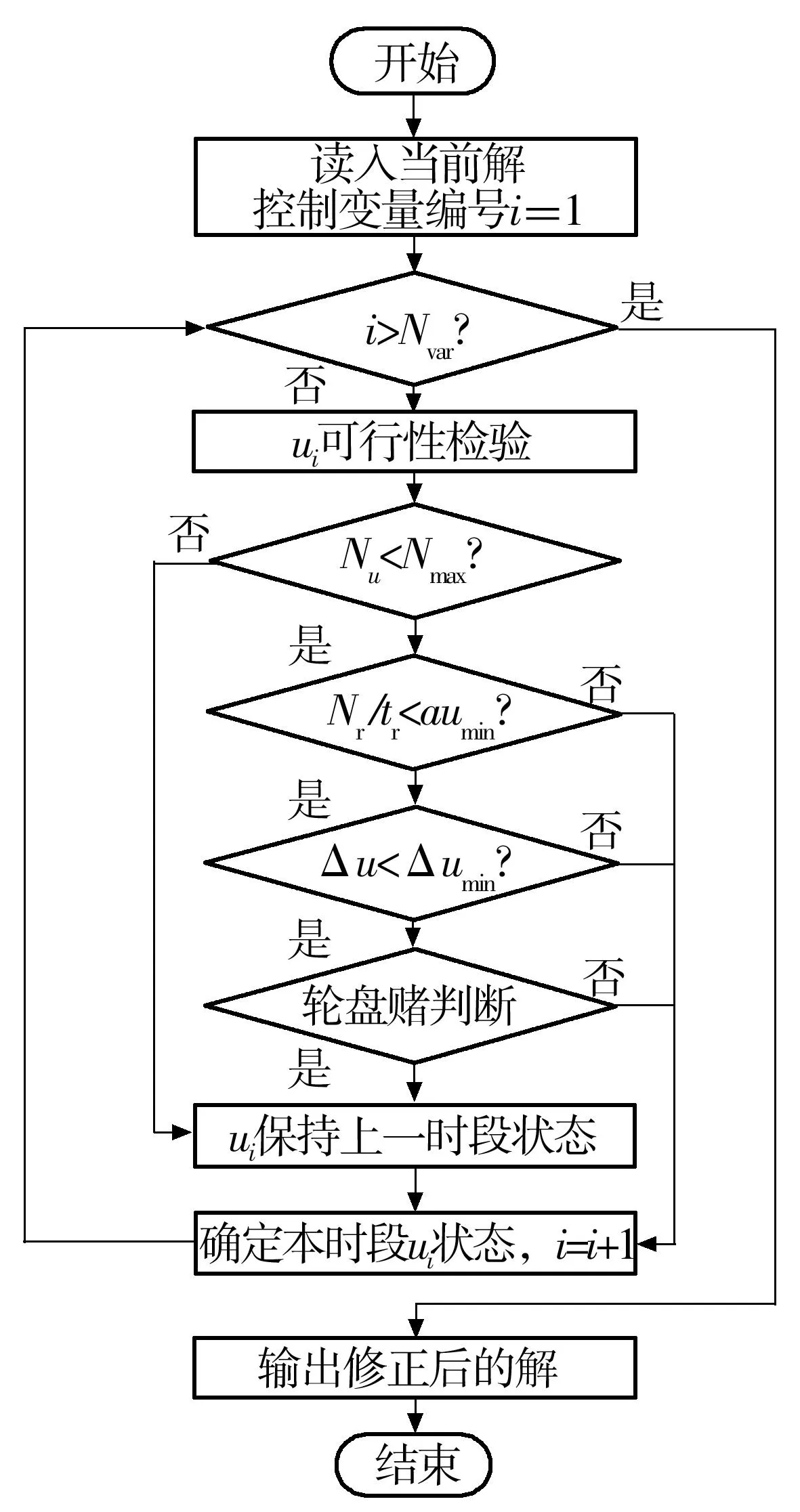
图5　修正环节流程图

根据本时段各控制设备的Nr/tr即剩余单位时段的设备可调节能力对设备的调整量Δu进行约束，同样通过轮盘赌操作的方式，在一定概率下对控制设备调整量低于限值的不必要动作加以回避，加快对趋优解的搜索速度.通过文中算法可根据优化进程中的控制设备状态量对控制设备的动作进行辅助修正，能够在各时段基于优化进程的信息做出趋优决策，实现含特殊负荷配电网的无功电压趋优控制.

3实例应用与结果分析

3.1测试系统

文中以标准IEEE33节点辐射形配电系统为基础，将部分节点的常规负荷替换为如下典型特殊负荷：在21、32节点处分别接入600 kW风力发电机，将5节点处的负荷设定为冶炼设备(波动负荷)，将10节点处的负荷设定为轧钢设备(冲击负荷)，并联电容器组安装位置为4、9、14、22及28节点，并联电容器组每组额定容量为50 kvar，每个安装位置各安装20组，日动作次数严格上限值Nmax取为5，而日动作次数期望上限值Nexmax取为3，实际配电网中可能还包含变压器抽头的调整，此处仅优化电容器的投切以验证算法效果.具体的系统接线图如图6所示.

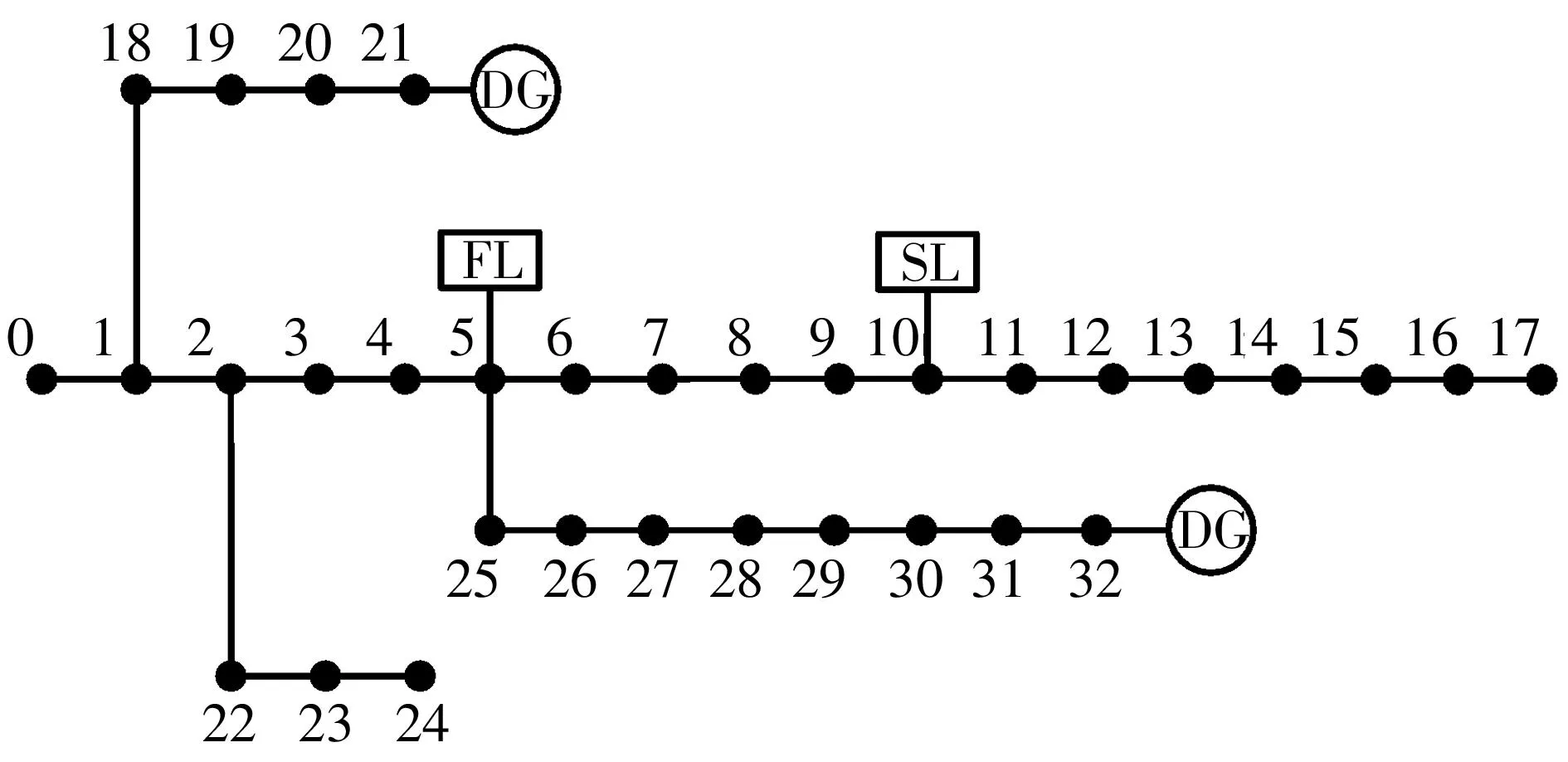
图6　修改后的IEEE33节点测试系统

图6所示系统中，特殊负荷接入点的功率采取概率模型，实例中根据典型特殊负荷(风力发电机、冶炼设备、轧钢设备)的实测功率曲线进行概率统计获得.其他常规负荷节点的负荷在各时段内均满足正态分布即式(1)-(2)，为了校验文中方法在对服从不同负荷变化规律的应用场景的适应性，各常规负荷节点全天24个时段的负荷期望值满足如图7所示的3种类型的阶梯状负荷曲线，同时取σP=σQ=0.1.

图7　常规负荷节点的3种日负荷曲线

Fig.7Three kinds of daily load curves of the conventional load node

图7中纵坐标负荷水平表征各时段该节点与测试系统中的标准负荷数据的相对值，测试系统中各常规负荷节点所对应的负荷曲线类型如表2所示.

表2常规负荷节点所对应的负荷曲线类型

Table 2Load curves corresponding to the conventional load nodes

负荷曲线类型所包含节点编号A1、2、6-9、11-13、16-20、25-30B3、4、22、25、31C14、15、23、24

考虑到DG出力随机性与预测难度，设定DG出力在全天24个时段内均采用概率模型，实际应用中可结合预测值采用时序概率模型.而考虑到一般生产规律，冶炼设备与轧钢设备接入点的功率需求仅在07：00至22：00内采用概率模型，其余非工作时段在低负荷状态下同常规负荷采取正态分布进行描述，特殊负荷的概率模型如图8所示.

图8　特殊负荷的概率模型

3.2结果分析

3.2.1随机潮流结果有效性分析

通过随机潮流计算可以获得配电网中各节点的电压95%概率区间，如图9所示.图中实线为各节点的电压期望值，两条虚线之间的区间为95%概率区间，即各节点电压分布概率累积密度函数中满足2.5%≤F(x)≤97.5%的区间范围.

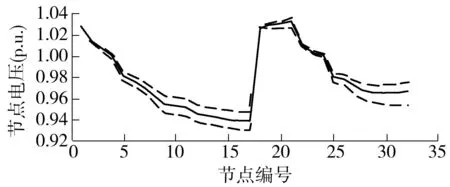
图9　配电网电压95%概率区间

Fig.9Voltage 95% probability interval of distribution network

由图9可知，在线路靠近首端的节点电压概率分布呈现较为集中的态势，而越靠近末端电压分布得越分散，即不确定性更强.

为验证随机潮流结果的有效性，分别采用基于半不变量法的配电网随机潮流计算方法和蒙特卡洛模拟法进行对比，其中蒙特卡洛模拟法的抽样规模取10 000次.以节点29电压分布概率密度函数为例，图10中连续点线为半不变量法解析计算结果，阶梯实线为蒙特卡洛法模拟结果，可见随机潮流计算与抽样模拟结果十分接近，可以有效地描述特殊负荷的不确定性.

3.2.2网损及设备动作情况分析

运用文中方法对动态无功优化问题进行求解，

图10　节点29测试结果

将优化结果与常规的静态无功结果进行对比，其中静态无功优化模型中特殊负荷节点均采用额定功率进行计算，优化算法同样采用MPGA.

可得到各节点的电容器组全天内的动作次数，如表3所示.以节点22的电容器组动作曲线为例，文中所提出的动态无功优化的动作次数相比于静态无功优化有了大幅度的下降，如图11所示:

表3　各控制设备动作次数对比

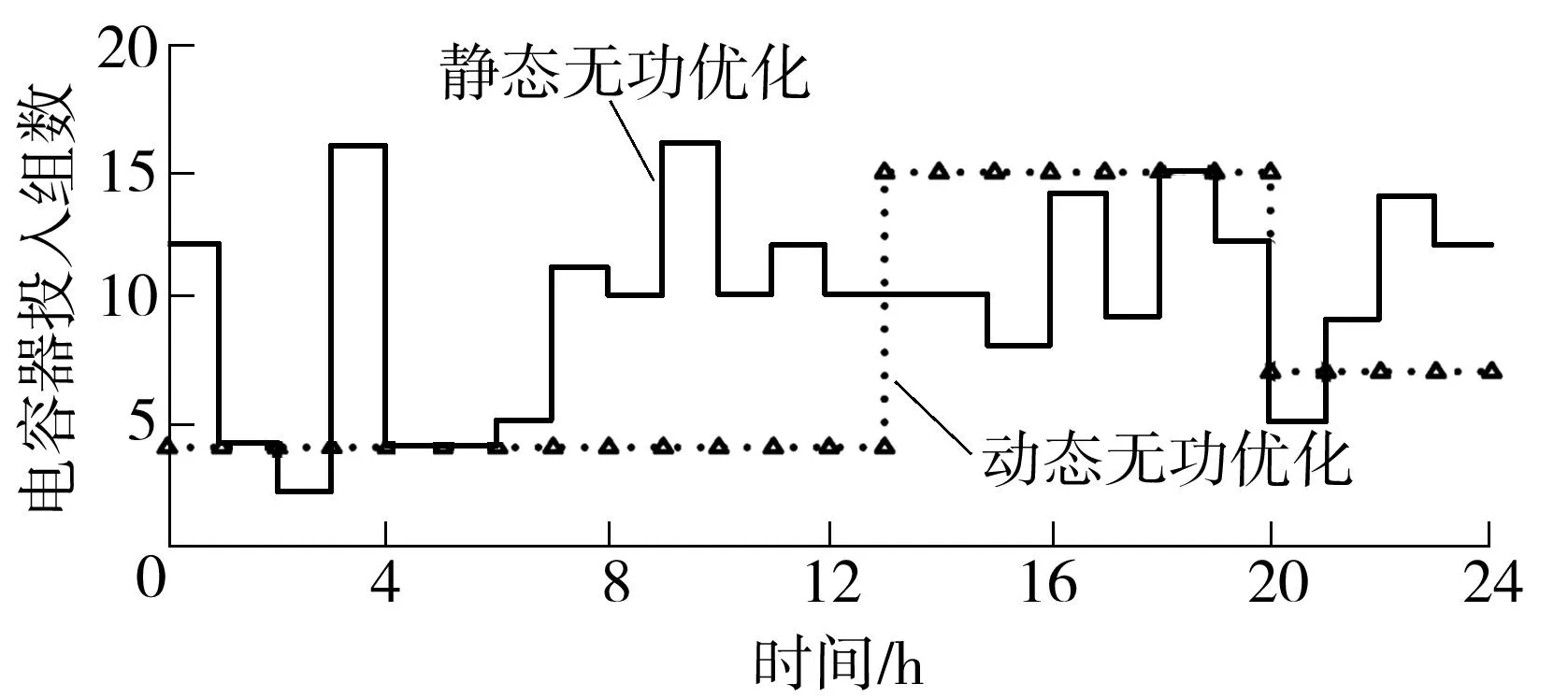
图11　节点22电容器组动作曲线

两种方法优化后各时段的网损期望值对比如图12所示.

由图12可知，动态无功优化各时段所求得的网损值基本上会略高于静态无功优化，但是并不会有明显的增加，而动作次数却得到了十分有效的控制.

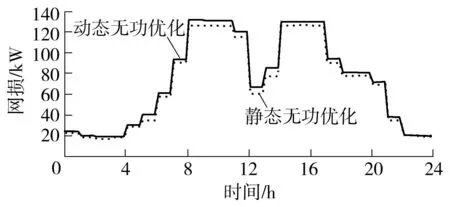
图12　网损期望值对比

当动作次数约束存在时，各电容器组由于受到较为严格的动作次数约束而未能充分投入，将会在一定程度上造成网损上升.测试表明，通过合理确定设备动作罚函数的控制参数，可控制设备的动作次数保证在期望动作次数附近，而随着动作次数约束值的放松，可有助于降低全天的整体网损值.

进一步分析各节点电容器组的动作时刻之间的关系，各节点电容器组动作时段如表4所示.

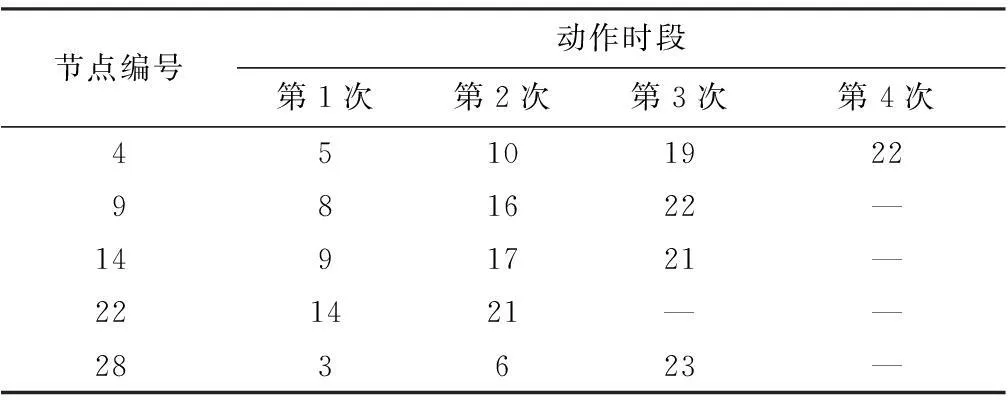
表4　各节点电容器动作时段

由表4可知，各节点的电容器组动作时刻基本不同，且在设备动作罚函数的作用下自主地形成了控制设备之间的配合模式，即形成一种“轮动”的动作方式.由于各控制设备的动作罚函数以自身的剩余单位时段的设备可调节能力作为基准，因此在各时段的优化计算中各设备动作的惩罚值是相互独立的，因此当某电容器组已经使用了较多的动作次数时，其相比于其余动作较少的电容器组会具有较低的动作权限，系统会优先以动作较少的电容器来参与本时段的无功调控.同时各个时刻各节点电容器组的轮流动作有效地减小了设备动作对系统的冲击和影响.

3.2.3配电网电压质量分析

以节点10补偿后全天的电压95%概率区间变化趋势进行分析，节点10补偿前后电压95%概率区间变化趋势如图13所示.

由图13可看出，补偿后全天内节点10的电压均得到了抬升，其中补偿后95%区间的电压下限最低也仅在0.98(p.u.)附近.

图13　节点10补偿前后电压95%概率区间变化趋势

Fig.13Trend of voltage 95% probability interval before and after the compensation of node 10

对比部分节点静态无功优化及文中动态无功优化方法所得的补偿效果，节点17及32在两种优化方案下的全天电压95%概率区间变化趋势如图14及15所示.

图14　节点17电压95%概率区间变化趋势

Fig.14Trend of voltage 95% probability interval of node 17

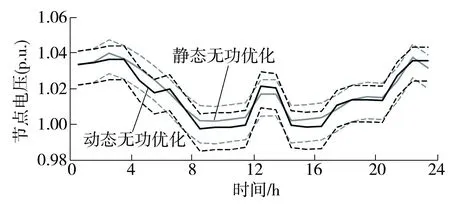
图15　节点32电压95%概率区间变化趋势

Fig.15Trend of voltage 95% probability interval of node 32

由图可知，两种优化方案对于电压质量的调控效果较为接近，由于电压质量罚函数的作用，可以将电压偏移有效地控制在0%～2.5%的满意区间，避免电压越限的潜在风险.同时，通过电压质量罚函数及设备动作罚函数两者控制参数的合理设计，可以合理地权衡在电压质量和设备动作之间取舍，实现冲突目标下的优化决策.

4结语

文中建立了含特殊负荷的配电网动态无功优化模型，以概率模型描述特殊负荷的不确定性，运用随机潮流求解状态变量的概率分布，全面反映特殊负荷接入后配电网的运行状态.针对离散控制设备动作次数约束造成动态无功优化问题的时空强耦合性，文中提出一种时段解耦策略以实现原问题的解耦并转化为逐时段连续优化决策，有效降低了求解难度.基于电压概率分布信息及设备调节能力分别设计了电压质量罚函数及设备动作罚函数，优化目标充分计及网损、电压概率分布以及设备调节能力的共同作用.实例分析表明，在罚函数作用下控制设备之间自主地形成了配合模式，实现配电网无功电压的趋优控制.所提出的方法在含特殊负荷的配电网实时无功电压控制、日前无功计划、智能配电网的无功优化配置等领域均有广阔的应用前景.

参考文献：

[1]陈旭,杨雨瑶,张勇军，等.光伏光照概率性对配电网电压的影响 [J].华南理工大学学报(自然科学版),2015,43(4):112- 118.

CHEN Xu，YANG Yu-yao，ZHANG Yong-jun，et al.Influence of illumination probablity of photovoltaic system on voltage of power distribution networks [J].Journal of South China University of Technology(Natural Science Edition),2015,43(4):112- 118.

[2]DJAPIC P，RAMSAY C，PUDJIANTO D,et al.Taking an active approach [J].IEEE Power and Energy Magazine，2007，5(4):68- 77.

[3]BASTIAO F，CRUZ P，FETEIRO R.Impact of distributed generation on distribution networks [C]∥Proceedings EEM 2008,5th International Conference on European Electricity Market.Lisboa:IEEE，2008:1- 6.

[4]刘明波，朱春明，钱康龄，等.计及控制设备动作次数约束的动态无功优化算法 [J].中国电机工程学报，2004,24(3):39- 45.

LIU Ming-bo，ZHU Chun-ming，QIAN Kang-ling，et al.Dynamic reactive-power optimization algorithm incorporating action number constraints of control devices [J].Proceedings of the CSEE，2004,24(3):39- 45.

[5]胡泽春，王锡凡.配电网无功优化的分时段控制策略 [J].电力系统自动化，2002,6:45- 49.

HU Ze-chun，WANG Xi-fan.Time-interval based control strategy of reactive power optimization in distribution networks [J].Automation of Electric Power Systems，2002,6:45- 49.

[6]王秀丽，李正文，胡泽春.高压配电网无功/电压的日分段综合优化控制 [J].电力系统自动化，2006,30(7):5- 9.

WANG Xiu-li，LI Zheng-wen，HU Ze-chun.Time-interval based comprehensive control strategy for daily voltage/VAR optimization in distribution systems [J].Automation of Electric Power Systems，2006,30(7):5- 9.

[7]方兴，郭志忠.配电网时变无功电压优化方法 [J].电力系统自动化，2005,29(9):40- 44,54.

FANG Xing，GUO Zhi-zhong.Optimal time-varying reactive power and voltage control in distribution systems [J].Automation of Electric Power Systems，2005，29(9):40- 44,54.

[8]蔡昌春，丁晓群，王宽，等.动态无功优化的简化方法及实现 [J].电力系统自动化，2008,32(5):43- 46,58.

CAI Chang-chun，DING Xiao-qun，WANG Kuan，et al.Simplified method of dynamic reactive power optimization and its implementation [J].Automation of Electric Power Systems，2008,32(5):43- 46,58.

[9]赵登福，刘昱，夏道止.考虑开关动作次数约束的配电网无功电压控制方法的研究 [J].西安交通大学学报，2003,37(8):783- 786.

ZHAO Deng-fu，LIU Yu，XIA Dao-zhi.Reactive power/voltage control of distribution system considering the constraint of the maximum allowable number of switching operations [J].Journal of Xi’an Jiaotong University，2003,37(8):783- 786.

[10]王淳，程浩忠，陈恳.配电网动态无功补偿的整体优化算法 [J].电工技术学报，2008,23(2):109- 114.

WANG Chun，CHENG Hao-zhong，CHEN Ken.Integrated optimization algorithm of dynamic reactive power for distribution system [J].Transactions of China Electrotechnical Society，2008,23(2):109- 114.

[11]谭煌，张璐，丛鹏伟，等.计及分布式电源与电容器协调的配电网日前无功计划 [J].电网技术，2014,38(9):2590- 2597.

TAN Huang，ZHANG Lu，CONG Peng-wei，et al.Day-ahead reactive power scheduling for distribution network considering coordination of distributed generation with capacitors [J].Power System Technology，2014,38(9):2590- 2597.

[12]陈海焱，陈金富，段献忠.含风电机组的配网无功优化 [J].中国电机工程学报，2008,28(7):40- 45.

CHEN Hai-yan，CHEN Jin-fu，DUAN Xian-zhong.Reactive power optimization in distribution system with wind power generators [J].Proceedings of the CSEE，2008,28(7):40- 45.

[13]何禹清，彭建春，毛丽林，等.含多个风电机组的配电网无功优化 [J].电力系统自动化，2010,34(19):37- 41.

HE Yu-qing，PENG Jian-chun，MAO Li-lin，et al.Reactive power optimization in distribution system with multiple wind power generators [J].Automation of Electric Power Systems，2010,34(19):37- 41.

[14]王淳，高元海.基于概率统计的含间歇性分布式发电的配电网无功优化 [J].电网技术，2014,38(4):1032- 1037.

WANG Chun，GAO Yuan-hai.Probability statistics based reactive power optimization of distribution network containing intermittent distributed generations [J].Power System Technology，2014,38(4):1032- 1037.

[15]张喆，李庚银，魏军强.考虑分布式电源随机特性的配电网电压质量概率评估 [J].中国电机工程学报，2013,33(13):150- 156.

ZHANG Zhe，LI Geng-yin，WEI Jun-qiang.Probabilistic evaluation of voltage quality in distribution networks considering the stochastic characteristic of distributed gene-rators [J].Proceedings of the CSEE，2013,33(13):150- 156.

[16]刘明波，简淦杨，董萍.孤岛微电网的随机潮流计算 [J].华南理工大学学报(自然科学版)，2014,42(4):13- 18.

LIU Ming-bo，JIAN Gan-yang，DONG Ping.Stochastic power flow calculation of islanded microgrids [J].Journal of South China University of Technology(Natural Science Edition)，2014,42(4):13- 18.

[17]杨欢，邹斌.含相关性随机变量的概率潮流三点估计法 [J].电力系统自动化，2012,36(15):51- 56.

YANG Huan，ZOU Bin.A three-point estimate method for solving probabilistic power flow problems with correlated random variables [J].Automation of Electric Po-wer Systems，2012,36(15):51- 56.

[18]丁明，李生虎，黄凯.基于蒙特卡罗模拟的概率潮流计算 [J].电网技术，2001,25(11):10- 14,22.

DING Ming，LI Sheng-hu，HUANG Kai.Probabilistic load flow analysis based on monte-carlo simulation [J].Power System Technology，2001,25(11):10- 14,22.

[19]蒋金良，林广明，欧阳森，等.改进灾变遗传算法及其在无功优化中的应用 [J].华南理工大学学报(自然科学版),2010,38(3):95- 100.

JIANG Jin-liang，LIU Guang-ming，OUYANG Sen，et al.Improved catastrophic genetic algorithm and its application to reactive power optimization [J].Journal of South China University of Technology(Natural Science Edition)，2010,38(3):95- 100.

[20]叶在福，单渊达.基于多种群遗传算法的输电系统扩展规划 [J].电力系统自动化，2000,5:24- 27,35.

YE Zai-fu，SHAN Yuan-da.A new transmission network expansion planning based on multiple-population genetic algorithm [J].Automation of Electric Power Systems，2000,5:24- 27,35.

Dynamic Reactive Power Optimization of Distribution Network Containing Special Load Based on Time Decoupling

OUYANGSenYANGJia-haoANXiao-huaCHENXin-hui

(School of Electric Power∥Key Laboratory of Clean Energy Technology of Guangdong Province, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:The expansion of special loads in power distribution networks results in uncertain power flow distribution, great voltage fluctuation and difficulties in the control of reactive power. In order to solve this problem, a dynamic reactive power optimization method of the distribution network containing special loads is proposed. In the investigation, first, the uncertainty of power flow in the distribution network containing special loads is described via the calculation of probabilistic load flow. Next, in order to overcome the strong space-time coupling of dynamic reactive power optimization issue created by the action constraints of the discrete control equipment, a time decoupling strategy is proposed, which transforms the original problem into a continuous optimization decision in each period. Then, a voltage quality penalty function and an equipment switch penalty function are designed based on the probabilistic voltage distribution information and the equipment adjustment ability.The optimization goal fully considers the network loss, the probabilistic voltage distribution and the equipment adjustment ability, so that the reactive voltage of the distribution network can be optimized according to the optimization process of control variables and state variables. Finally, a case study on IEEE 33-bus system is performed to verify the effectiveness of the proposed method.

Key words:power distribution network; dynamic reactive power optimization; time decoupling; special load; probabilistic load flow; multi-population genetic algorithm

doi：10.3969/j.issn.1000-565X.2016.02.015

中图分类号：TM 711

文章编号：1000- 565X(2016)02- 0097- 10

作者简介：欧阳森(1974-)，男，博士，副研究员，主要从事电能质量、节能技术与智能电器研究.E-mail：ouyangs@scut.edu.cn

*基金项目：国家自然科学基金重点项目(50937001)；华南理工大学中央高校基本科研业务费专项资金资助项目(2012ZM0018)

收稿日期：2015- 06- 01

Foundation item: Supported by the National Natural Science Foundation of China(50937001)