高速铁路连续式无砟轨道温度场分析

刘付山，曾志平,2，吴 斌，张志超

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075)

处于自然环境中的无砟轨道结构承受周期性太阳辐射等环境因素的作用，其温度场变化是环境因素对轨道结构最主要作用的综合体现之一[1,2]。与有砟轨道结构相比，无砟轨道结构的整体性和稳定性较好，但对温度变化更敏感。现阶段对无砟轨道结构温度场的研究较少，在考虑温度荷载作用时，大多仅考虑竖向温度梯度取最大值时一维温度场的变化情况[3-6]，温度荷载加载时较少考虑轨道结构内部温度变化规律和时变特性。

借鉴混凝土路面温度场研究经验，轨道结构温度场分析方法可归纳为两类：一是统计分析的方法，即基于实测数据，采用概率统计方法回归分析，得到轨道板温度场与主要因素的关系，以此估算轨道板的温度场。文献[3, 7]对单元板式无砟轨道温度场进行实测，但由于测点有限，未能形成对轨道板温度场的全面了解。文献[8]对CRTSⅡ型轨道板纵断面上不同深度温度进行长期观测，并基于日最高气温提出轨道板最大温度梯度预估模型，由于缺少对太阳辐射、风速等相关因素的考虑，这一预估模型有一定的局限性。二是理论分析法，即通过对自然环境的模拟，基于传热学基本原理，采用数值分析方法计算结构温度场。现阶段在轨道结构温度场分析中采用这一方法的较少。

本文通过对自然环境的模拟，基于气象学基本理论，建立连续式无砟轨道结构温度场分析三维有限元模型，以CRTSⅡ型板式轨道结构为例，在考虑轨道板内温度时变特性的基础上，分析不同时刻轨道板内温度场、太阳不对称照射、太阳辐射、砂浆层热传导性能、温度骤变对轨道板温度场的影响。

1 轨道结构温度场分析模型及边界换热条件

1.1 轨道结构三维温度场有限元模型

利用有限元软件ANSYS建立CRTSⅡ型板式无砟轨道结构温度场分析模型，如图1所示。模型中采用三维热实体单元分别模拟轨道板、砂浆层、底座/支承层，表面边界条件、层间接触边界条件均满足传热学基本原理[8]。

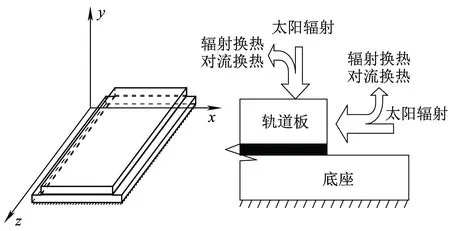
图1 温度场分析模型

CRTSⅡ型无砟轨道板是纵向连续结构，在有限长度内，可以将纵连后的轨道板视为沿长度温度无变化、沿高度和宽度方向上温度有变化的瞬态热传导问题，轨道板内的温度场可表示为

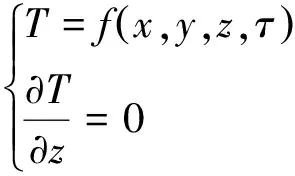
(1)

式中：T为轨道板内任意一点的温度；x、y、z分别为轨道板宽度、高度和长度方向的坐标；τ为时间。

1.2 导热微分方程

根据能量守恒与转化定律，在不考虑混凝土自身内热源发热的情况下，其导热微分方程为

(2)

式中：Ti为轨道结构第i层的温度；ai=λi/(ρici)，λi为第i层导热系数，J/(m·s·K)，ρi为第i层密度，kg/m3，ci为第i层比热容，J/(kg·K)。

1.3 边界条件

1.3.1 轨道板表面边界条件

已知大气温度和大气辐射时，可将轨道板表面边界条件归为第三类边界条件，根据牛顿冷却定律，轨道板表面热平衡方程为

受太阳照射的表面

(3)

未受太阳照射的表面

(4)

式中：T为轨道板温度场；n为法线方向上的单位矢量；αs为轨道板表面对太阳辐射的吸收率；Q(τ)为太阳辐射随时间变化的函数；σ为斯蒂芬-玻尔兹曼常数，σ=5.67×10-8W/(m2·K4)；ε为表面发射率；Ta和Ts为大气和轨道板表面温度；Tak和Tsk分别为大气和轨道板表面绝对温度，其中Tak=Ta+273.15，Tsk=Ts+273.15。

1.3.2 接触面边界条件

未发生离缝等病害的情况下，轨道板与砂浆层、砂浆层与支承层/底座各层间紧密接触，满足传热学第四类接触条件，即接触面的温度相等，通过接触面的热流密度也相等。

1.3.3 下表面边界条件

随着轨道结构深度的增加，温度和温度梯度变化幅度逐渐减小，当深度超过20 cm时，温度基本趋于稳定且波动较小[7]。在不考虑季节性温度变化的情况下，支承层/底座下表面的温度变化幅度较小，同时桥上CRTSⅡ型板式轨道结构底座与桥梁间铺设的“两布一膜”对底座与桥梁间的热量传递有一定阻隔。综上，在建立温度场模型时忽略底座与桥梁的热传导。

1.4 环境因素的模拟

处于自然环境中的轨道结构，热量主要来源为大气温度变化与太阳辐射[9]。本文主要模拟这两个环境因素的影响。

1.4.1 大气温度变化

气温变化受到较多因素影响，变化复杂，但晴天气温变化尚有一定的规律遵循。文献[9]在研究道路结构温度时采用双正弦函数组合模拟气温变化规律，即

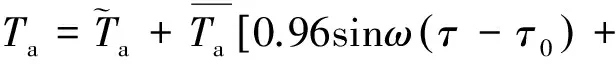
(5)

1.4.2 太阳辐射

太阳以电磁波形式向外辐射能量，其投射到轨道板的总能量，部分被轨道板表面吸收，其余被轨道板表面反射。太阳辐射能量从日出开始逐渐增大，正午达到最大值，然后逐渐减弱，至日落时消失，Q(τ)夜间为0。Q(τ)随时间的日变化规律为[9]

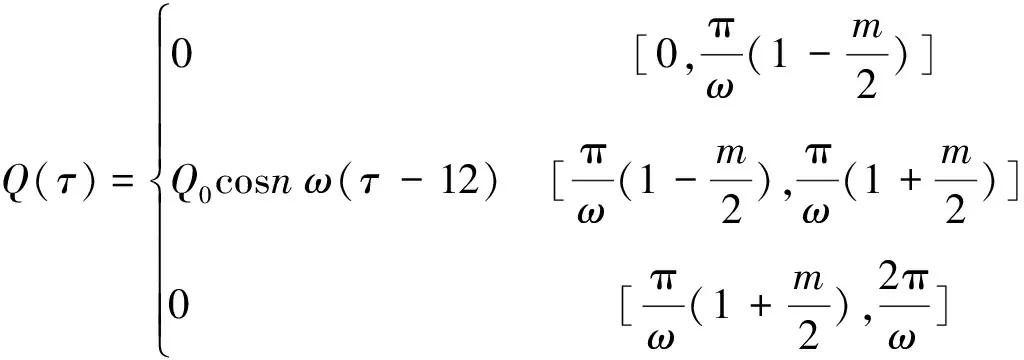
(6)

式中：Q0为正午时最大辐射能量，Q0=0.131mQd，Qd为日辐射总能量；m=12/c，c为实际日照时间。

1.5 初始温度场

轨道结构温度场初始条件较复杂，但在相同环境条件下，反复加载多次后，轨道结构温度场趋于稳定，反映到实际情况中便是长期相对稳定天气时，轨道结构内所形成的温度场。本文计算中，均选用多次重复加载后的结果，以消除初始条件对计算结果的影响。

2 轨道结构温度场模型验证及分析

2.1 轨道结构温度场模型验证

从气象局获得广州市2012年7月1日气象数据如下：日最高气温35 ℃，最低气温26.6 ℃，日太阳辐射总量22.82 MJ/m2，平均风速1.5 m/s。模型中材料热工参数见表1，砂浆层热工参数参考沥青混凝土选取。在水泥混凝土路面温度场研究中，混凝土路面对太阳辐射吸收率实测值一般为0.6～0.63，考虑轨道板表面较光滑，轨道板表面太阳辐射吸收率取0.6。先考虑轨道结构温度场对称的情况，轨道板上表面和底座上表面受到太阳直接照射，侧表面仅考虑与大气间换热，计算结果如图2、图3所示。

表1 计算参数

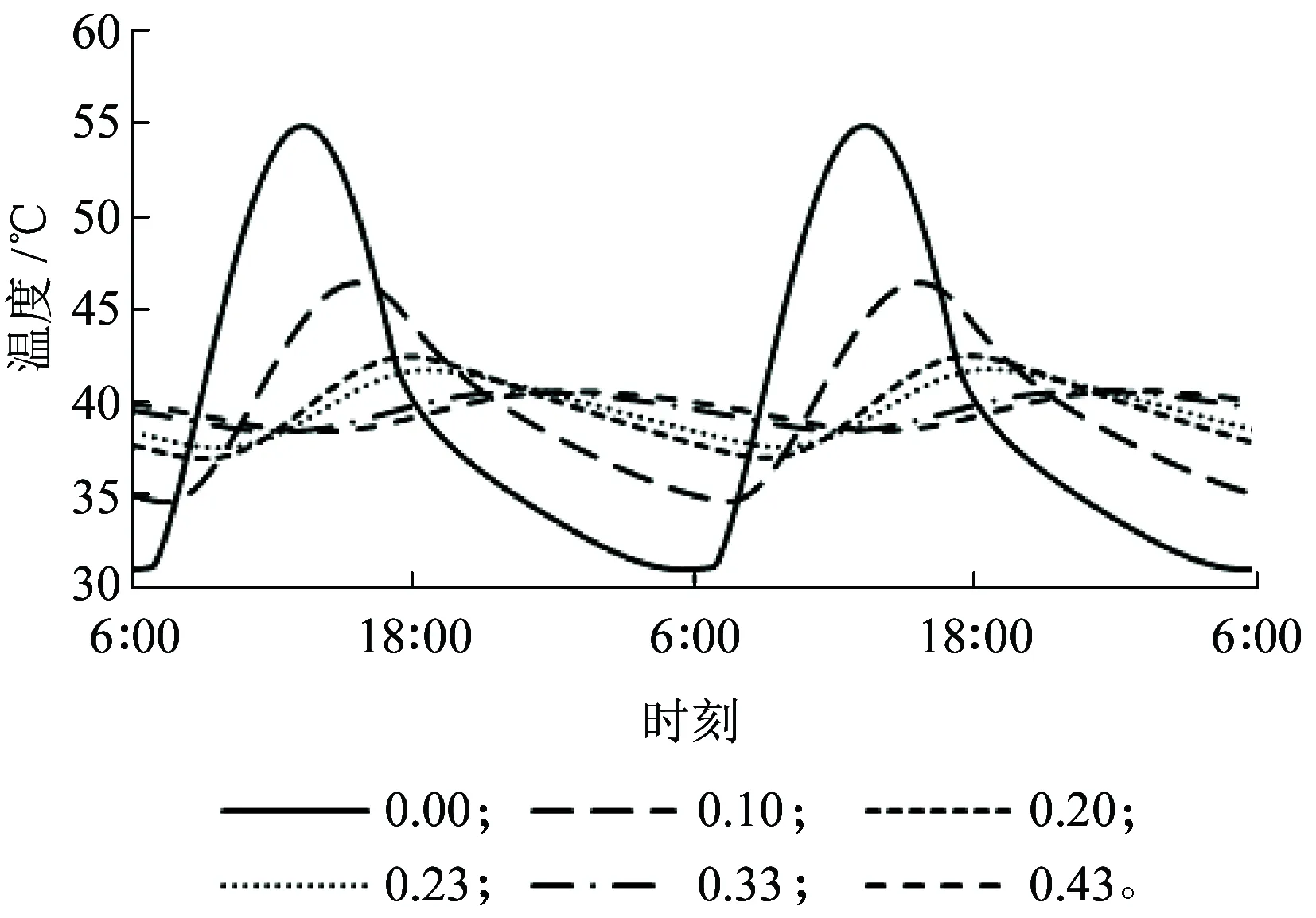
注：图例中数值表示距表面的深度，m。图2 轨道结构内距表面不同深度处温度变化曲线

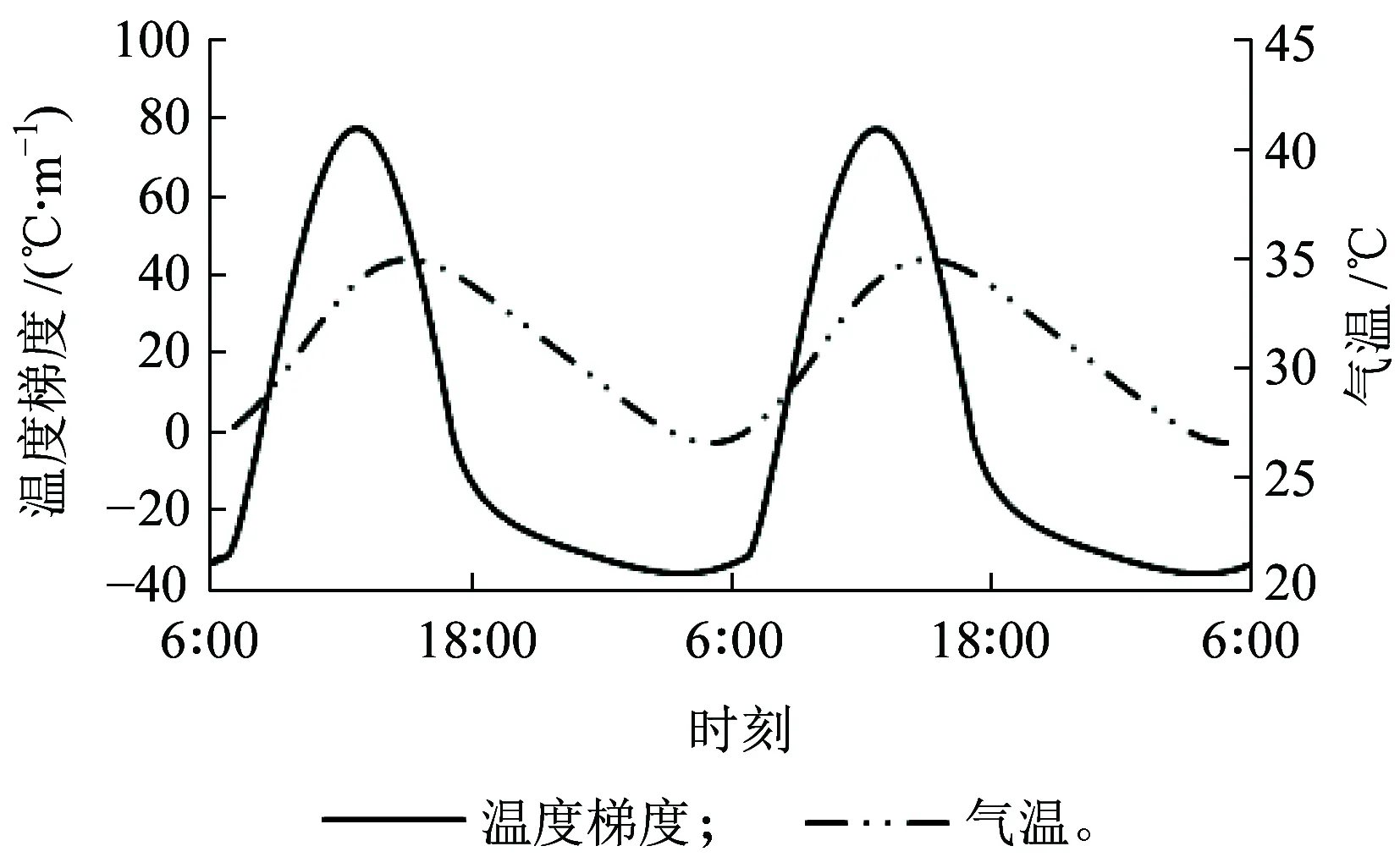
图3 轨道板温度梯度变化曲线

从图2、图3可以看出，轨道结构内不同深度处温度随着太阳辐射和气温周期性变化，随着深度增加，温度波动幅度变小，峰值出现时间逐渐滞后。通过与文献[7]中实测曲线对比，图2和图3中曲线与实测曲线的线形和变化趋势一致。但文献[7]仅对气温进行观测，提出的温度场预估模型只考虑了气温变化，未考虑太阳辐射，本文模型同时考虑了气温与太阳辐射的影响，因此无法与其进行数据对比。

砂浆层、底座/支承层中心纵断面上温度及温度梯度变化幅度较小，与文献[7]实测结果相同，因此本文重点研究轨道板温度场。

另外，文献[10]选用太阳日辐射量、日最高气温和日温差作为气象因素变量，在实测数据基础上建立二元和一元回归关系式，已应用于我国水泥混凝土路面设计规范[11-12]。

Tg·m=0.086+0.003 4ΔTa+0.000 267 5Q

(7)

Tg·m=0.109+0.000 272 3Q

(8)

式中：Tg·m为轨道板最大温度梯度，℃/m；ΔTa为日气温温差，℃；Q为太阳日辐射量，J/cm2。回归关系(7)、(8)计算结果与实际观测值的相关系数分别为0.854和0.843，标准残差分别为0.103和0.104，式(7)、式(8)可以比较准确地估计混凝土路面最大温度梯度值[11-12]。

由上式计算得到混凝土标准板一维热传导时的温度梯度最大值，将其换算成20 cm厚混凝土板最大温度梯度，与本文中模型计算得到的板中纵断面上的温度梯度最大值进行对比，其结果见表2。

表2 温度梯度计算结果比较

从表2可以看出，本文模型对晴天轨道结构温度场模拟具有较好适应性。

2.2 轨道板温度场分析

不同时刻轨道板内纵断面温度和温度梯度沿深度变化曲线如图4、图5所示。从图4、图5可以看出，不同时刻轨道板内温度沿深度并非线性变化，轨道板温度梯度沿深度方向逐渐减小，高温时刻的温度梯度随深度变化较大，这是由于在高温时刻，大量热量流入轨道板，同时，由于混凝土的导热性能较差，存在热量积累，越靠近表面积累的热量越多，导致越靠近表面温度梯度变化越大。

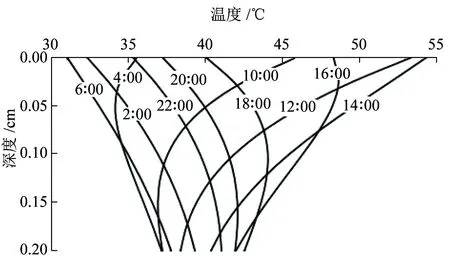
图4 不同时刻轨道板内温度沿深度变化曲线

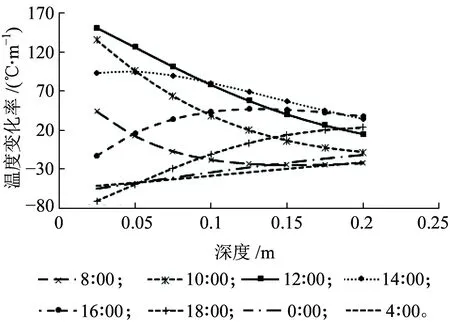
图5 不同时刻轨道板内温度梯度沿深度变化曲线

3 轨道板温度场影响因素分析

3.1 太阳辐射的影响

太阳辐射是轨道结构温度场热量的主要来源之一。由于实际线路走向、受太阳照射面不同，太阳辐射不同；同时太阳辐射随季节变化，混凝土的不断老化也影响轨道板表面对太阳辐射的吸收能力。

3.1.1 太阳辐射对轨道板板边影响

对于不同走向的线路，轨道板侧表面接受日照的时间不同，图6～图9分别列举了单侧日照情况下轨道板横向温度变化以及温度梯度变化情况。

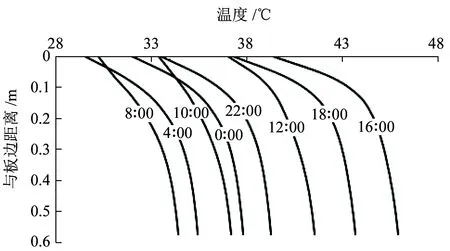
图6 板边未受日照面不同时刻横向温度变化曲线

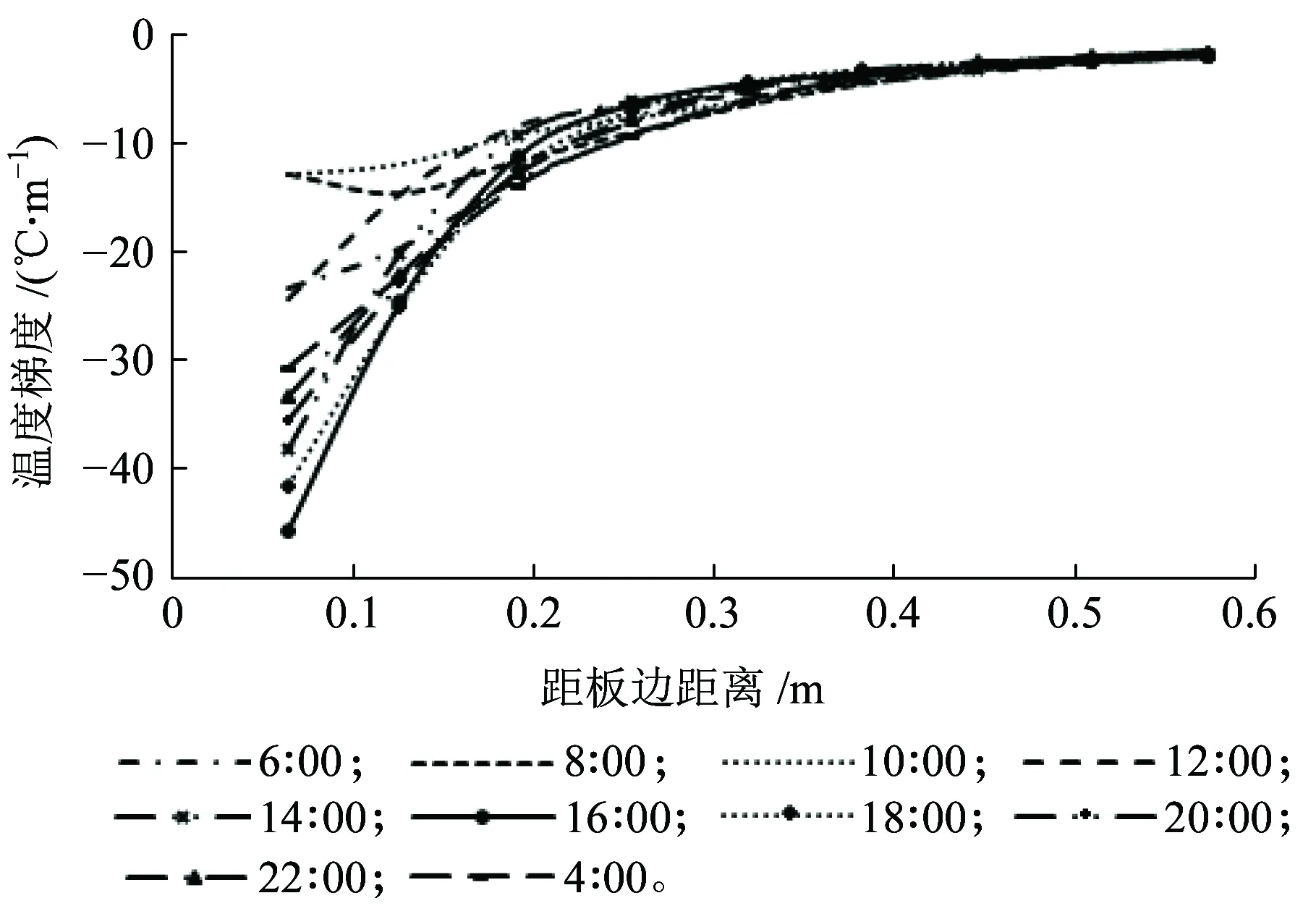
图7 板边未受日照面不同时刻横向温度梯度变化曲线

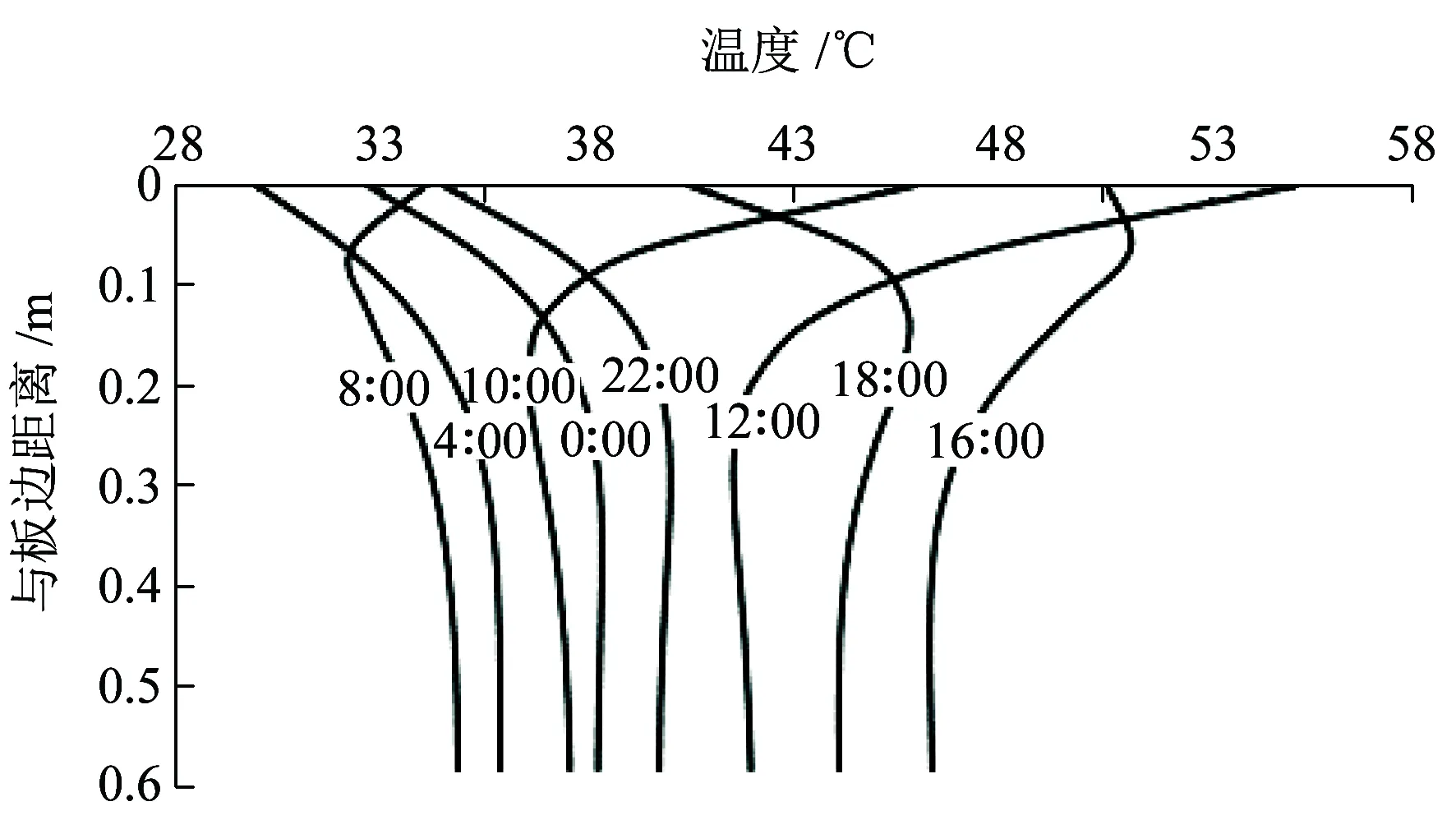
图8 板边受日照面不同时刻横向温度变化曲线

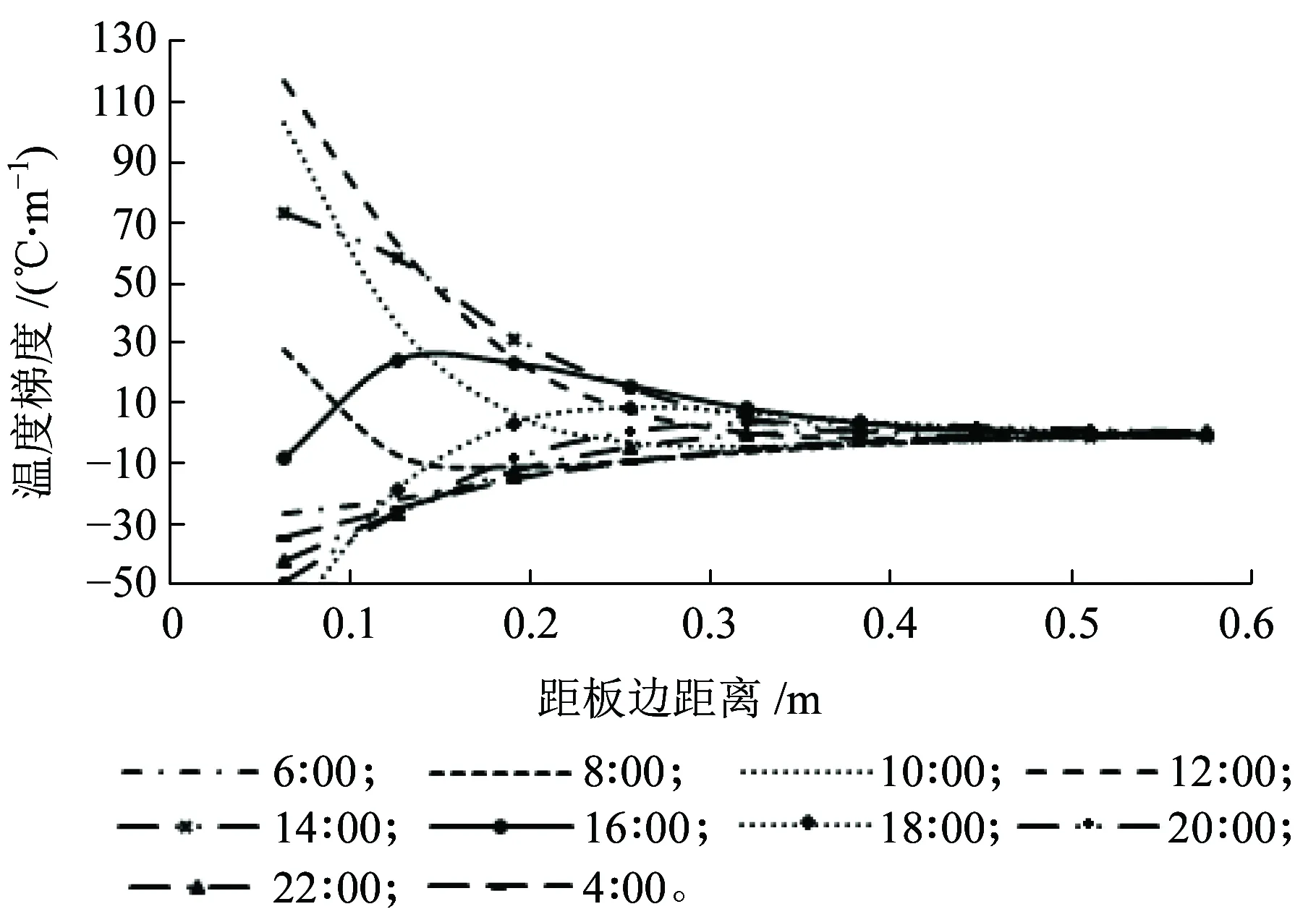
图9 板边受日照面不同时刻横向温度梯度变化曲线

从图6～图9可知，轨道板横向温度梯度的影响范围有限，没有因为日照影响而明显增加，随着距板边距离的增大，横向温度梯度逐渐减小，当距板边超过40 cm时，横向温度梯度趋近于0。轨道板侧表面未受太阳照射的一侧，均呈现负温度梯度，即外冷内热的情况；轨道板侧表面受太阳照射的一侧，横向温度梯度变化较大，距板边越近，温度梯度变化越大，正温度梯度(外热内冷)最大值大于负温度梯度(外冷内热)最大值。

轨道板上表面受日照影响，温度高于大气温度，热量沿高度方向向下传导，未受到日照的侧表面由于其温度高于大气温度，热量由轨道板流向大气环境，导致侧表面温度较轨道板内部低，横向表现为负温度梯度。受太阳照射一侧，由于热量由上表面流入的同时也从侧表面流入，混凝土的导热性差使热量聚集，导致受日照的侧表面温度较内部高，表现为正温度梯度。

3.1.2 太阳辐射对轨道板温度场的影响

CRTSⅡ型轨道板采用工厂预制的施工方式，安装初期表面平整光滑，但在环境因素的周期作用下，混凝土逐渐老化，对太阳辐射的吸收能力也随之变化，此因素也可视为太阳辐射量不同对轨道板温度场的影响。最大温度梯度和轨道板表面温度随吸收率变化曲线如图10、图11所示。

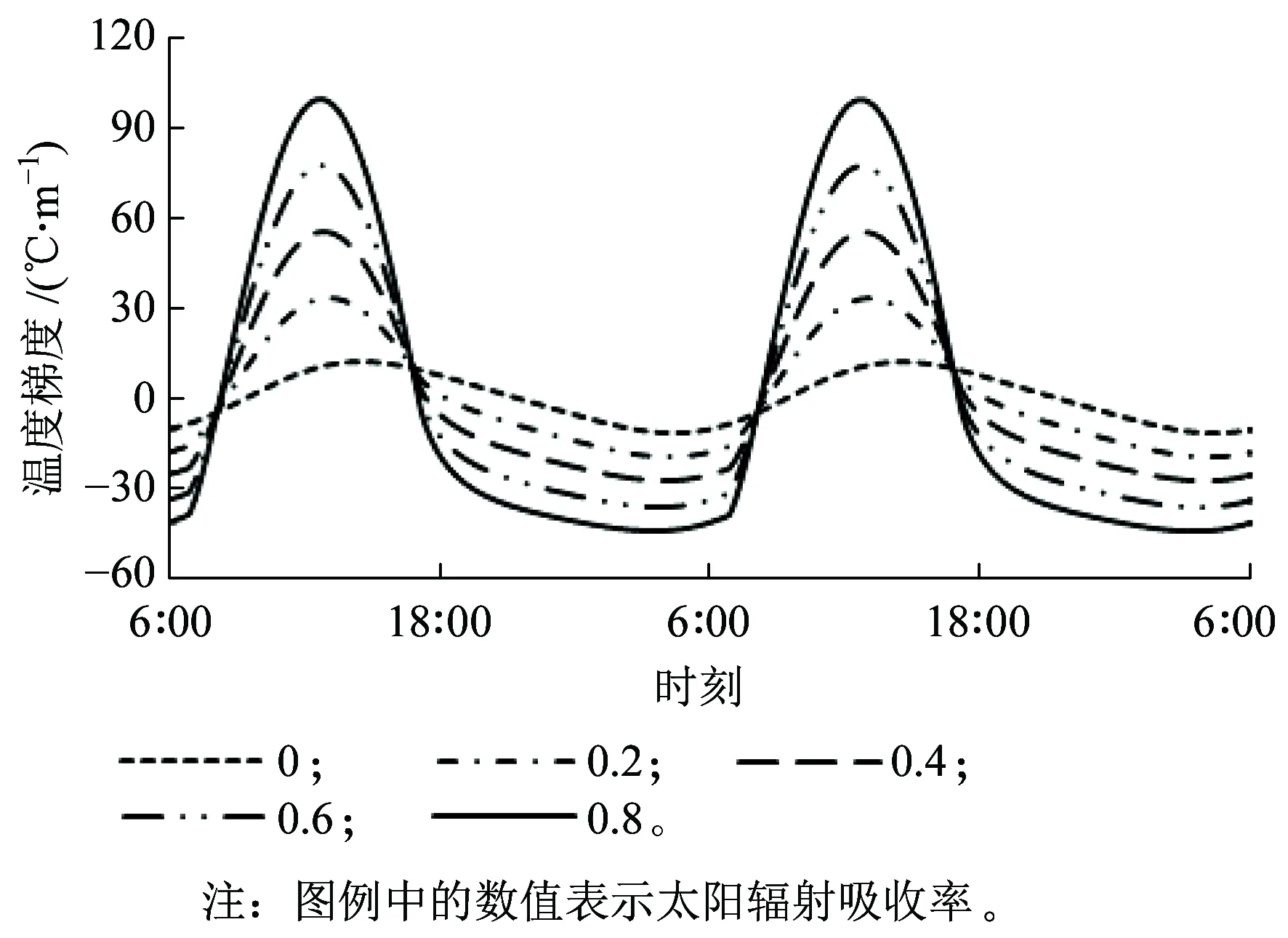
图10 轨道板温度梯度变化曲线

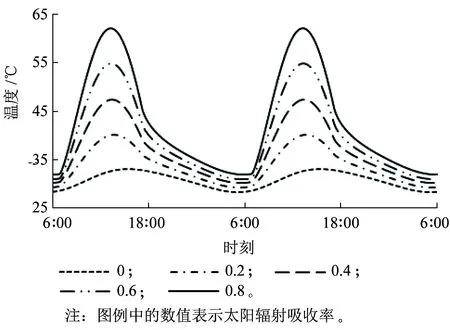
图11 轨道板表面温度变化曲线

从图10、图11可知，随着对太阳辐射吸收程度的增加，轨道板表面温度和温度梯度的波动幅度逐渐增大，在对太阳辐射吸收很小的情况下，即阴天或者无法直接接受日照的地段，轨道板温度梯度和表面温度变化较小。由此可见，太阳辐射是影响轨道板最大温度梯度和表面温度的重要因素之一。

3.2 风速对轨道板温度场的影响

风速对轨道结构温度场的影响主要体现在表面总换热系数的不同。研究表明混凝土表面换热系数与风速线性相关，风速越大，表面总换热系数越大[13]。本文通过换热系数对温度场的影响研究风速对温度场的影响，计算结果如图12～图14所示。从图12～图14可知，随着表面总换热系数的增大，轨道板温度梯度和表面温度逐渐减小，但减小速率逐渐变缓。

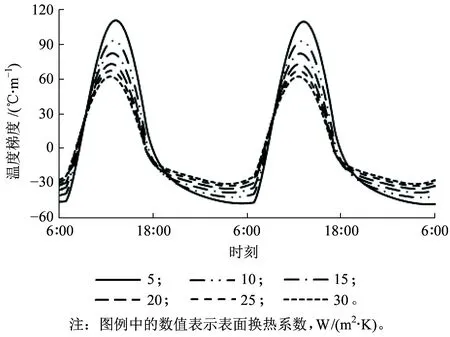
图12 轨道板温度梯度变化曲线

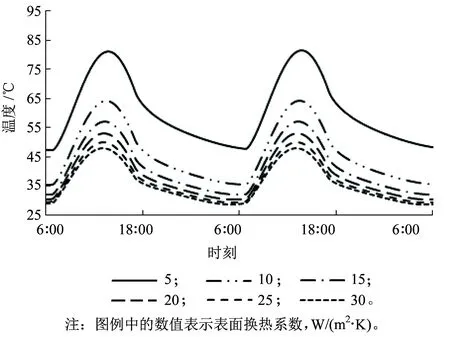
图13 轨道板表面温度变化曲线

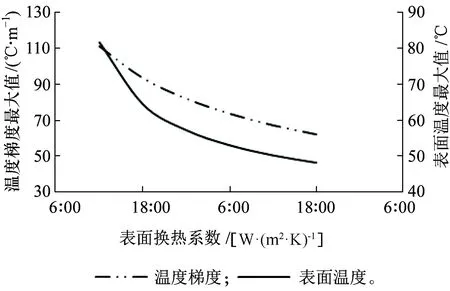
图14 表面温度最大值和温度梯度最大值变化曲线

3.3 砂浆层热传导性能对轨道板温度场影响

水泥乳化沥青砂浆层由乳化沥青和水泥按一定比例配合而成[14]，目前关于其热力学性能的研究较少。本文将砂浆层导热系数由0.1 J/(m·s·K)上升到1.5 J/(m·s·K)，发现轨道板温度梯度最大值仅下降4.2 ℃/m，轨道板上、下表面温度最大值变化较小，由此可见，砂浆层的导热性能对轨道板温度场影响较小。

同时，轨道板与砂浆层的离缝、脱空将导致轨道板与砂浆层间热传导下降。此类工况可将其等效为砂浆层导热性能下降，因此，局部离缝脱空等病害对轨道板的温度场影响较小。

3.4 环境温度变化速度对轨道板温度场影响

由于自然环境变化的复杂性，轨道结构在运营期间，环境温度变化时快时慢，甚至还存在着环境温度骤变的情况。本文选取“骤变”“缓变”“长期不变”三种不同环境温度变化速度进行计算。“骤变”即短时间之内天气改变，计算时假设一天之中天气突然变化。“缓变”即天气在长时间内缓慢改变，计算时考虑计算效率，环境温度分5天缓慢变化。“长期不变”即天气情况保持长期不变的状态。计算工况和气象参数见表3、表4，不同计算工况下的轨道板温度梯度变化时程曲线如图15所示，不同工况温度梯度最大值见表5。

表3 计算工况

表4 气象数据

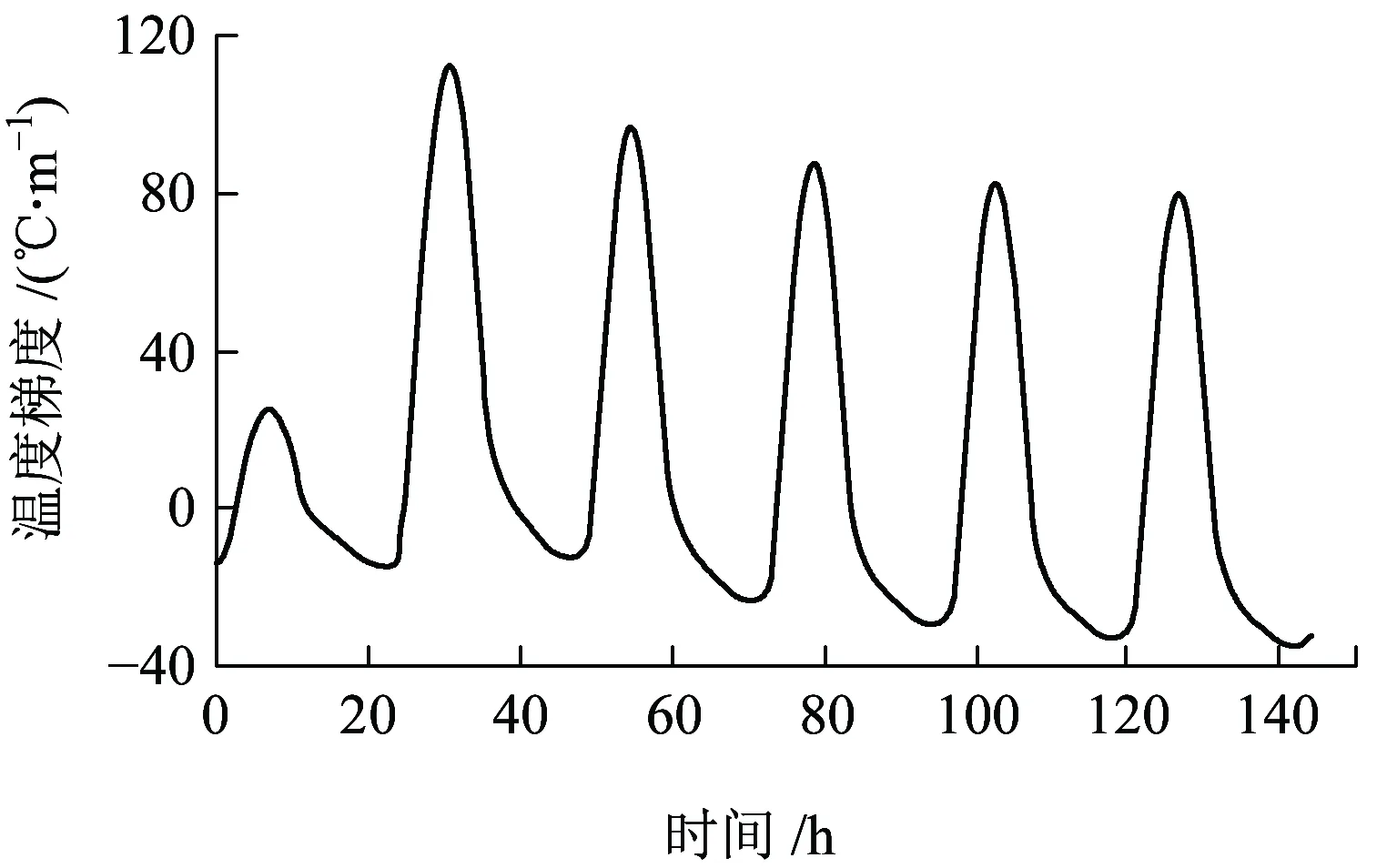
(a) 工况1

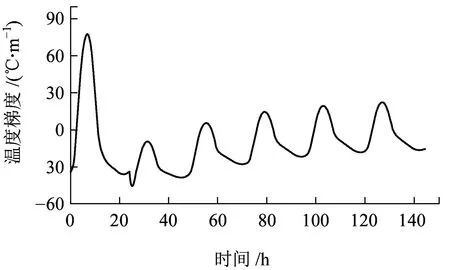
(b) 工况2

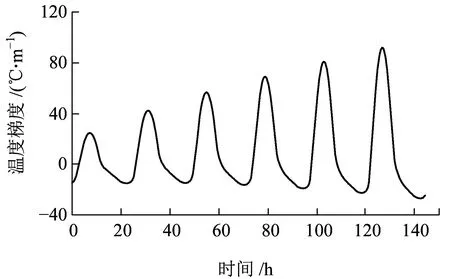
(c) 工况3

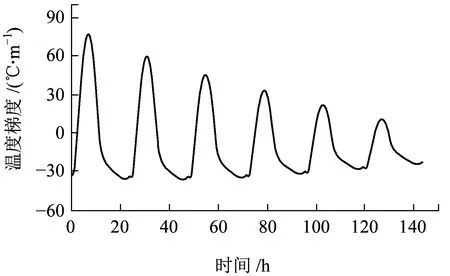
(d) 工况4

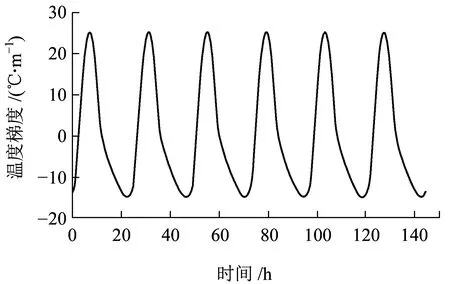
(e) 工况5

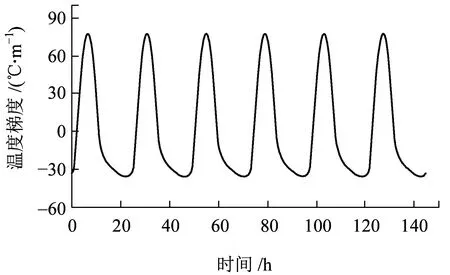
(f) 工况6图15 不同工况轨道板温度梯度变化曲线

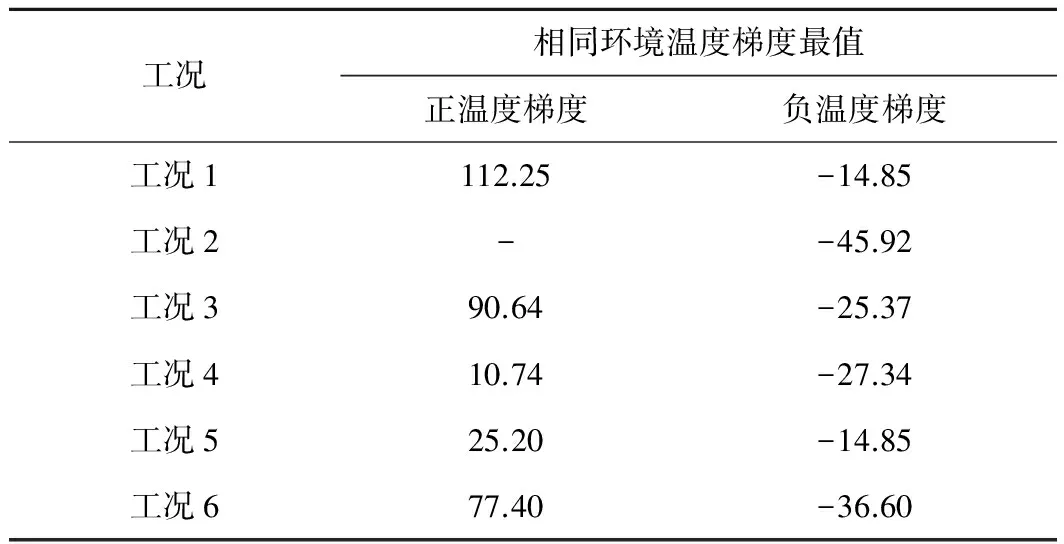
表5 不同工况温度梯度最大值 ℃/m

从图15可知，在温度骤变的过程中，温度梯度陡然增大，后逐渐趋于稳定。通过对气温骤变、气温缓慢变化、气温长时间稳定时相同环境的温度梯度最大值对比可以发现，环境升温过程中，升温速度越快，轨道板正温度梯度最大值越大，负温度梯度绝对值的最大值越小；环境降温过程中，降温速度越快，负温度梯度绝对值最大值越大，正温度梯度值越小。在研究轨道板温度梯度时，应充分考虑环境温度变化速度对温度梯度的影响。

4 结论

本文基于传热学基本原理，建立高速铁路连续式无砟轨道结构温度场分析模型，以CRTSⅡ型轨道板温度场为研究对象，通过参数分析，得出如下结论：

(1)不同时刻，轨道板纵断面温度和温度梯度随深度呈非线性变化。随着深度增加，温度梯度逐渐减小。

(2)轨道板侧表面受太阳照射对轨道板温度场影响有限，当距板边超过40 cm时，横向温度梯度趋近于0。受太阳照射一侧的横向温度梯度随时间变化较大，未受太阳照射一侧呈现负温度梯度，即外冷内热的情况。

(3)随着太阳辐射减小，轨道板温度梯度波动幅度逐渐减小。随着风速、表面总换热系数减小，轨道板温度梯度极值逐渐增大。

(4)砂浆层导热性能对轨道板温度场影响较小，轨道板与砂浆层间的离缝、脱空等对轨道板温度场影响较小。

(5)环境升温过程中，升温速度越快，轨道板正温度梯度最大值越大，负温度梯度绝对值的最大值越小。环境降温过程中，降温速度越快，负温度梯度绝对值的最大值越大，正温度梯度值越小。

(6) 轨道板表面太阳幅射吸收率、砂浆层热物理性质等关键参数的合理取值需进一步研究。

参考文献：

[1]石现峰，李建斌. 温度对板式无砟轨道结构的影响研究[J]. 铁道工程学报，2008(5)：30-32.

SHI Xianfeng, LI Jianbin. Research on Temperature Effect on the Structure of Slab Ballastless Track[J]. Journal of Railway Engineering Society, 2008(5):30-32.

[2]卫军，班霞，董荣珍. 温度作用对CRTSⅡ型无砟轨道结构体系的影响及损伤分析[J]. 武汉理工大学学报，2012，34(10)：80-85.

WEI Jun, BAN Xia, DONG Rongzhen. Study of Effects and Damage of CRTSⅡ Ballastless Track Structure System Induced by Temperature[J]. Journal of Wuhan University of Technology, 2012, 34(10):80-85.

[3]刘钰，赵国堂. CRTSⅡ型板式无砟轨道结构层间早期离缝研究[J]. 中国铁道科学，2013，34(4)：1-7.

LIU Yu, ZHAO Guotang. Analysis of Early Gap between Layers of CRTS Ⅱ Slab Ballastless Track Structure[J]. China Railway Science, 2013, 34(4):1-7.

[4]唐进锋，尹华拓，曾志平，等. 温度梯度作用下板式无砟道岔岔区板力学特性分析[J]. 铁道科学与工程学报, 2011,8(1): 24-28.

TANG Jinfeng, YIN Huatuo, ZENG Zhiping, et al. Mechanical Characteristic of Slab Track on Switch Area Under Temperature Gradient[J]. Journal of Railway Science and Engineering, 2011, 8(1):24-28.

[5]王继军，尤瑞林，王梦，等. 单元板式无砟轨道结构轨道板温度翘曲变形研究[J]. 中国铁道科学，2010，31(3)：10-14.

WANG Jijun, YOU Ruilin, WANG Meng, et al. Research on the Slab Temperature Warping of the Unit Slab Track System[J]. China Railway Science, 2010, 31(3):10-14.

[6]王森荣，孙立，李秋义，等. 无砟轨道轨道板温度测量与温度应力分析[J]. 铁道工程学报，2009(2)：52-55.

WANG Senrong, SUN Li, LI Qiuyi, et al. Temperature Measurement and Temperature Stress Analysis of Ballastless Track Slab[J]. Journal of Railway Engineering Society, 2009(2):52-55.

[7]刘钰，陈攀，赵国堂. CRTSⅡ型板式无砟轨道结构早期温度场特征研究[J]. 中国铁道科学，2014，35(1)：1-6.

LIU Yu, CHEN Pan, ZHAO Guotang. Study on the Characteristics of Early Temperature Field of CRTS Ⅱ Slab Ballastless Track Structure[J]. China Railway Science, 2014, 35(1):1-6.

[8]章熙民，任泽霈，梅飞鸣，等. 传热学[M]. 5版. 北京：中国建筑工业出版社，2007：10-22.

[9]陈嘉祺，罗苏平，李亮，等. 沥青路面温度场分布规律与理论经验预估模型[J]. 中南大学学报:自然科学版，2013，44(4)：1647-1656.

CHEN Jiaqi, LUO Suping, LI Liang, et al. Temperature Distribution and Method-experience Prediction Model of Asphalt Pavement[J]. Journal of Central South University:Science and Technology, 2013,44(4)：1647-1656.

[10]宋存牛. 层状路面结构体非线性温度场研究概况[J]. 公路，2005(1)：49-53.

SONG Cunniu. General Situation of Studies on Non-linear Temperature Field in Layered Pavement Structural System[J]. Highway, 2005(1):49-53.

[11]刘学毅，赵坪锐，杨荣山，等. 客运专线无砟轨道设计理论与方法[M]. 成都：西南交通大学出版社，2010：106-109.

[12]谢国忠，袁宏，姚祖康. 水泥混凝土路面最大温度梯度值[J]. 华东公路，1982, 6:9-19.

XIE Guozhong, YUAN Hong, YAO Zukang. The Maximum Temperature Gradient of Cement Concrete Pavements[J]. East China Highway, 1982, 6: 9-19.

[13]张建荣，刘照球. 混凝土对流换热系数的风洞实验研究[J]. 土木工程学报，2006，39(9): 39-43.

ZHANG Jianrong, LIU Zhaoqiu. A Study on the Convective Heat Transfer Coefficient of Concrete in Wind Tunnel Experiment[J]. China Civil Engineering Journal, 2006, 39(9):39-43.

[14]元强，曾志平. 控制CRTSⅡ型板式无砟轨道充填层砂浆与轨道板离缝技术研究报告[R]. 长沙：中南大学，2013.