喷射混凝土受压损伤本构模型研究

关 虓， 牛荻涛， 王家滨， 吴 博

(西安建筑科技大学 土木工程学院，陕西 西安 710055)

喷射混凝土是借助喷射设备，在压力作用下，通过输送管道，将按一定比例配合好的拌合料高速喷射到受喷面并瞬时压密的混凝土。喷射混凝土由喷射砂浆发展而来，其特性与普通混凝土大致相同，但与普通混凝土相比，喷射混凝土有不同的成分，材料有不同的特性。近年来，喷射混凝土因具有施工便捷、成本低廉、结构性能良好等优点，被广泛应用于隧道、边坡、地下硐室的支护以及建筑结构的加固防护工程[1-5]。因此，系统研究喷射混凝土的基本力学特性，对其在工程中更好地应用具有重要意义。

随着损伤理论的迅速发展，混凝土材料损伤性质的研究取得一定进展[6-9]。文献[10-11]引进内时理论，建立钢纤维混凝土的轴心受压损伤本构模型。文献[12]将宏观混凝土构件看作由无穷多个微元体组成，以各微元体强度为研究对象，考虑微元体强度的离散性，确定损伤变量的概型分布，建立混凝土损伤本构模型。这些研究大多限于普通混凝土以及常规施工工艺的各种掺和料混凝土，针对喷射混凝土损伤性质的研究较少。

现阶段，针对喷射混凝土的研究主要关注试验方法、施工技术、工程实际应用性等方面[13-15]，对于喷射混凝土基本力学性能的研究较少，考虑其损伤性质的本构模型的研究更少。本文在普通混凝土损伤本构模型研究基础上，根据文献[16]提出的平行杆模型(PBS)，考虑损伤阈值及塑性应变对本构关系的影响，分别对普通混凝土和喷射混凝土进行单轴受压试验研究，分析损伤阈值对本构模型的影响机制，确定损伤变量的概型分布，建立喷射混凝土的损伤本构模型。

1 喷射混凝土损伤本构方程的建立

将喷射混凝土试件看作由无穷多微元体组成，各微元体的极限强度(即破坏应变)是一个随机变量，假设微元体的破坏应变服从某一分布函数F(x)，且F(x)在x取值空间域中连续，则有

F′(x)=f(x)

(1)

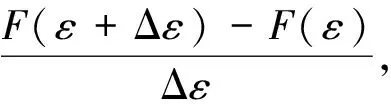
(2)

式中：f(x)为微元体破坏应变服从的概率密度函数；F(x)为其概型分布函数。

式(2)反映了试件整体应变为ε时，f(ε)在其邻域(ε±Δε,Δε→0)范围内的密集程度，即变化率。

损伤变量是材料损伤程度的一种度量指标，损伤度大小与发生破坏的微元体数量有关，微观层面上的微元体破坏越多，宏观层面上的损伤度越大，即微元体的破坏应变ε与损伤变量D之间存在某种映射关系g(ε)，令

(3)

式(3)反映了损伤变量的变化率，则g(ε)与f(ε)具有相同的函数性质和几何意义，有

(4)

对式(4)进行积分，可得

(5)

研究喷射混凝土的本构模型时，可将混凝土试件应变ε分为弹性应变与塑性应变两部分。根据文献[17]，可将Helmholtz自由能势表示为

Φ(εe,D,εp)=Φe(εe,D)+Φp(εp,D)

(6)

式中：D为损伤内变量；εe为弹性应变；εp为塑性应变。

混凝土损伤是不可逆过程，能量耗散应为非负值，故应满足热力学第二定律中的Clausius-Duheim不等式，即

(7)

式中：Φ为Helmholtz状态函数。

对式(7)进行微分，则有

(8)

由于εe的任意性，可得

(9)

将式(5)、式(6)代入式(9)，可以得到喷射混凝土损伤本构方程。

σ=E0(ε-εp)[1-D(ε)]

(10)

2 试验概况

2.1 试验原材料及配合比

试验所用水泥为秦岭牌P.O42.5普通硅酸盐水泥；渭河河砂，细度模数3.4；粗骨料为粒径5～10 mm的米石，级配连续；聚羧酸盐高性能减水剂；Ⅱ级粉煤灰；粉状速凝剂。试件水胶比为0.43。具体配合比见表1，其中编号PC表示普通混凝土，PA表示喷射混凝土。

表1 混凝土配合比

2.2 试验方法

喷射混凝土试件采用现场喷大板法制作，3 h后脱模移入隧道内养护7 d，随后切割加工成标准试件，放入标准养护室内养护21 d。本次试验共制作63个棱柱体试件(其中PC组31个，PA组32个)，试件尺寸100 mm×100 mm×300 mm，用于轴心受压试验。试验采用上海华龙测试仪器有限公司生产的WAW-1000微机控制电液伺服万能试验机、YHD-10位移传感器及TDS-602数据采集仪。本次试验采用人工采点，采取加载过程中的力和位移值。最小加载速率为0.1mm/min。加载装置示意如图1所示。

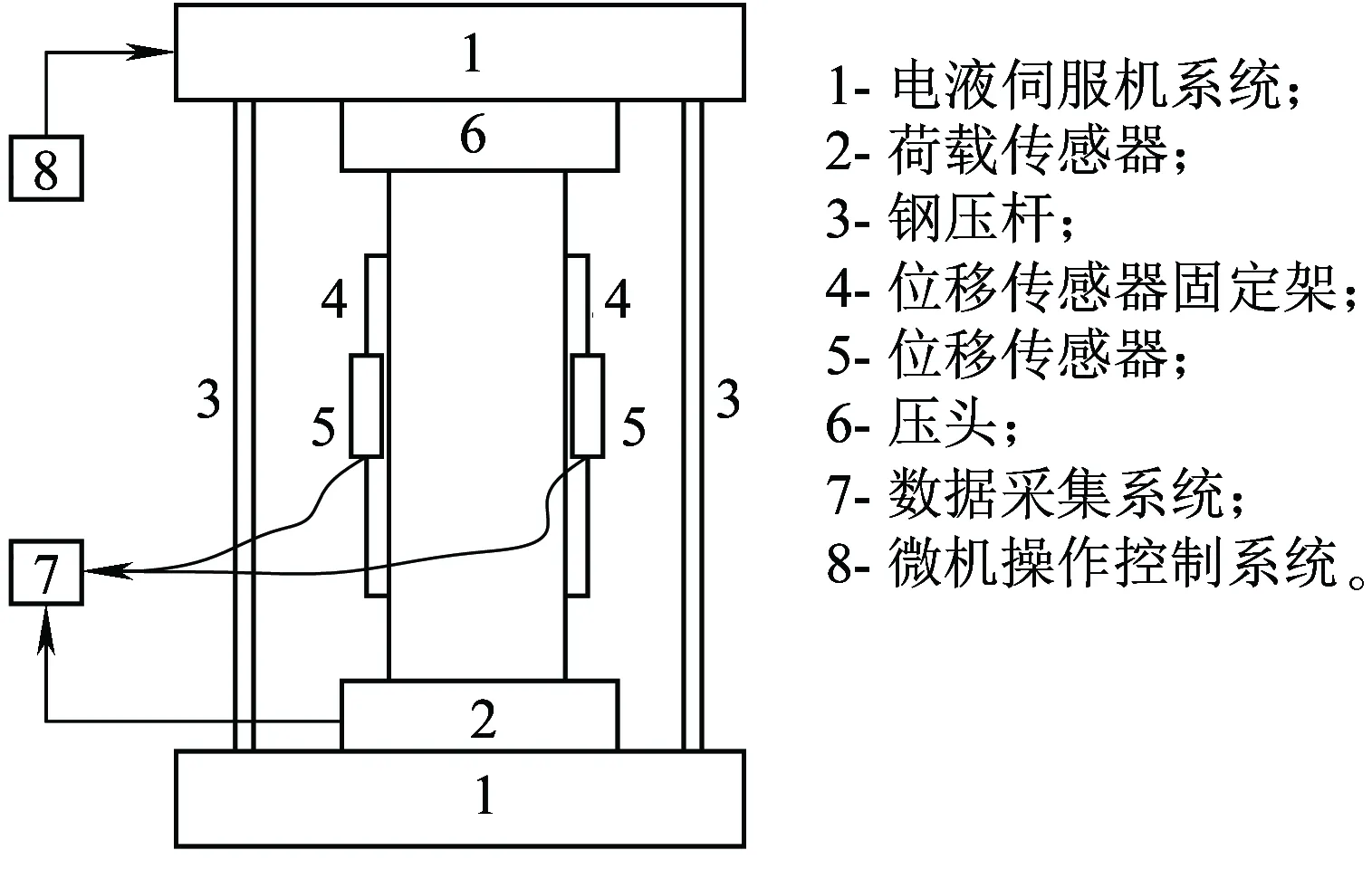
图1 加载装置示意

3 损伤变量的确定

两组混凝土单轴受压应力-应变曲线峰值应力、峰值应变的统计特性见表2。

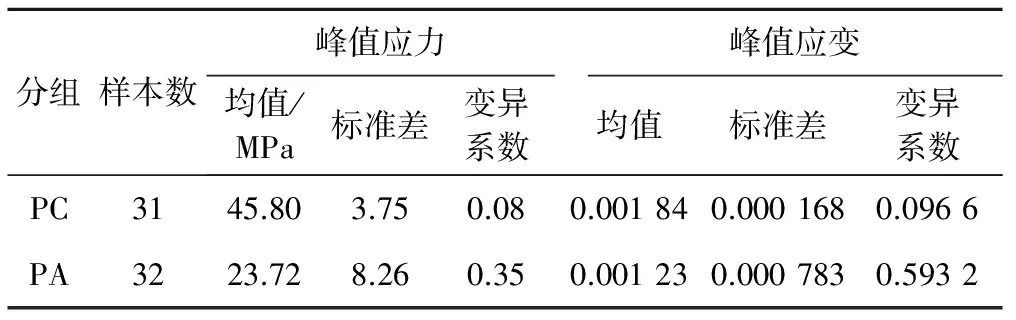
表2 峰值应力和峰值应变统计结果

从表2可以看出，喷射混凝土的峰值应力、峰值应变均小于普通混凝土，这是因为喷射混凝土中的速凝剂含有碱性成分，使喷射混凝土的成分特性异于普通混凝土；同时，整个养护周期内，其内部水化规律不同于普通混凝土，最终造成宏观层面上峰值应力、峰值应变的差异。

假定两组试件峰值应变均服从三参数Weibull分布，采用卡方法进行检验，显著水平α=0.05，三参数Weibull分布函数可以表示为

(11)

其均值与方差分别为

(12)

(13)

式中：η为形状参数；γ为阈值参数；a、b、c可通过中位秩公式[18]求得；Γ为伽马函数。

基于二阶矩法，并结合试验数据确定三参数γ、m、η的估计值，见表3。

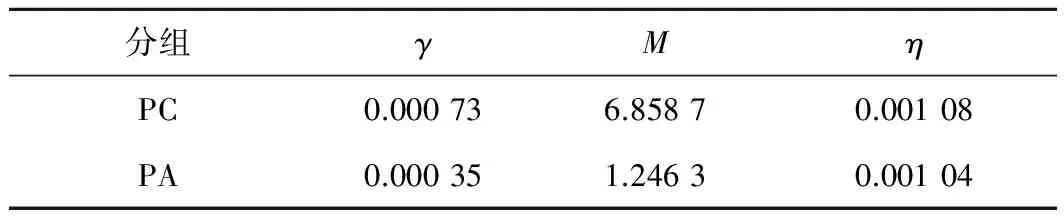
表3 Weibull分布函数参数估计值

具体检验步骤为：

(1)假设H0：三组试验的峰值应变服从Weibull分布；

(2)根据试验计算实测频数mi；

(3)计算理论频率pi和理论频数Npi；

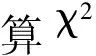
根据检验步骤，对不同试验结果进行计算检验，其检验结果见表4。

表4 Weibull分布检验结果

由表4可以看出，两组试件的峰值应变均服从Weibull分布，将式(11)代入式(10)，得到混凝土统计损伤本构模型为

(14)

式中：γ为损伤阈值，在达到损伤阈值前，试件处于弹性阶段，即无损伤。

4 喷射混凝土统计损伤本构模型

4.1 参数的计算

根据单轴受压σ-ε曲线的特点可以得到两个边界条件：

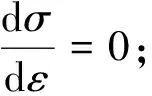
(2) 当σ=σc(峰值应力)时，ε=εc。

对式(14)求导，将两边界条件代入求导结果，得

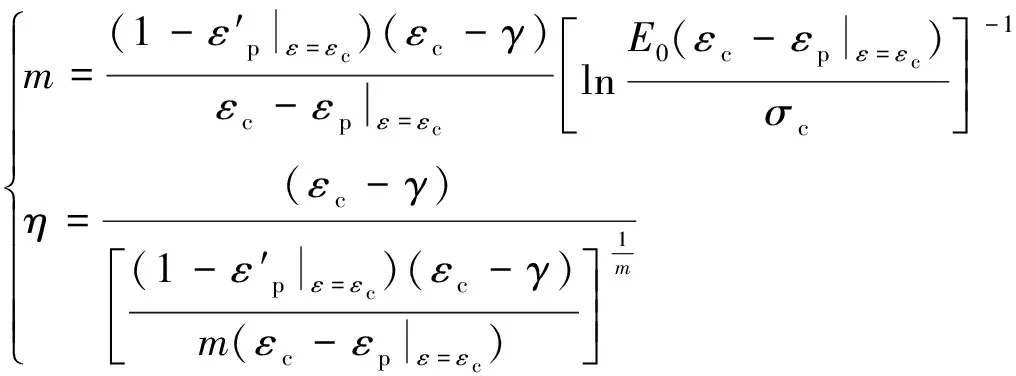
(15)

4.2 γ的取值

由式(15)可确定本构模型的参数m和η，这两个参数有明确的物理意义，损伤阈值γ常由经验判断，本文分析对比不同γ取值时应力应变曲线与试验曲线的拟合情况，以此讨论γ对普通混凝土和喷射混凝土本构模型的影响。具体结果如图2所示。

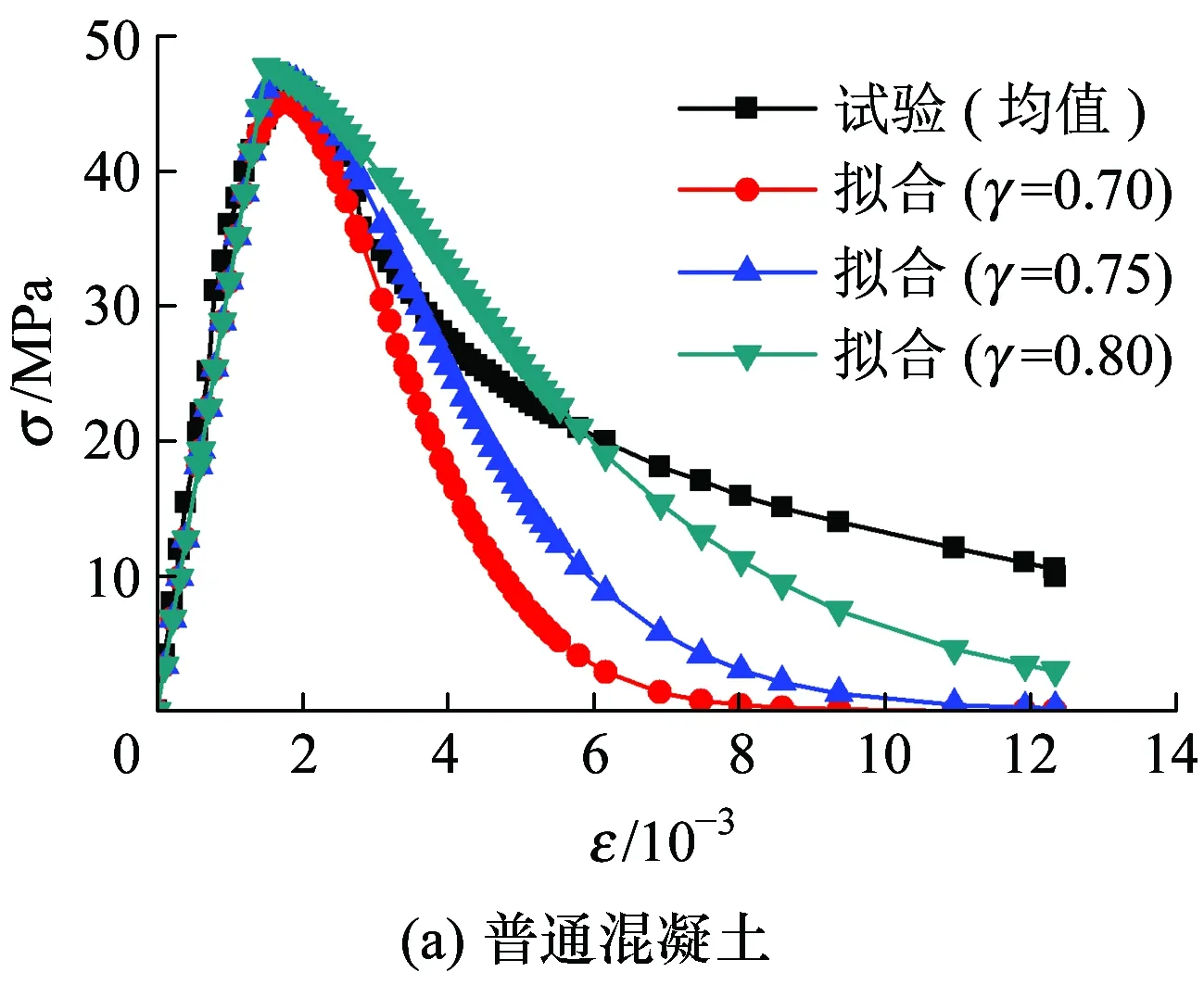
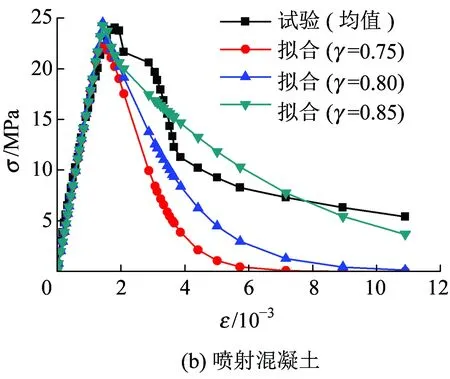
图2 不同损伤阈值γ的应力应变曲线

由图2(a)可知，对普通混凝土而言，损伤阈值γ取值为0.80倍峰值应力时与试验曲线的拟合度为最佳，峰值点后的下降段较其他两条曲线能够更好拟合试验曲线。由图2(b)可知，对喷射混凝土而言，当γ取值为0.85倍峰值应变时，拟合曲线与试验曲线的拟合度为最佳，且下降段能更好地拟合试验曲线。同时可以看出，随着损伤阈值γ的逐渐增大，峰值应力稍有增大，下降段曲线越来越平缓，材料延性增强，残余强度也逐渐提高，说明损伤阈值在某种程度上可以反映喷射混凝土残余强度特性。

4.3 喷射混凝土统计损伤本构模型

将试验数据代入式(15)中，可求得参数m和η。对m、η、γ进行统计分析，假定三者均服从正态分布，对假定的概型分布进行卡方检验，结果为接受假定。三个参数的统计分析结果见表5、表6。

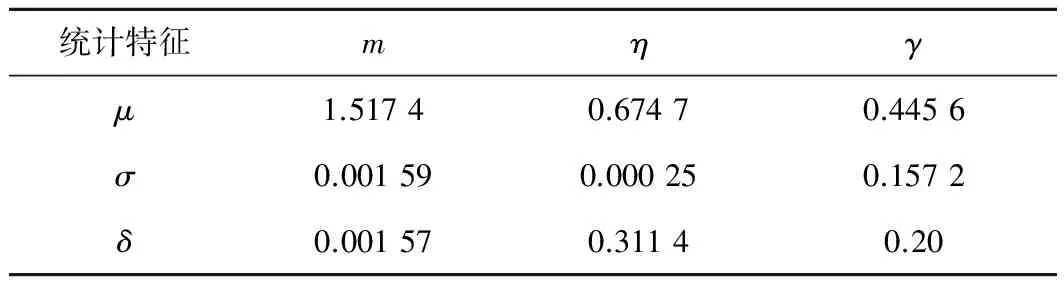
表5 普通混凝土本构模型参数统计结果

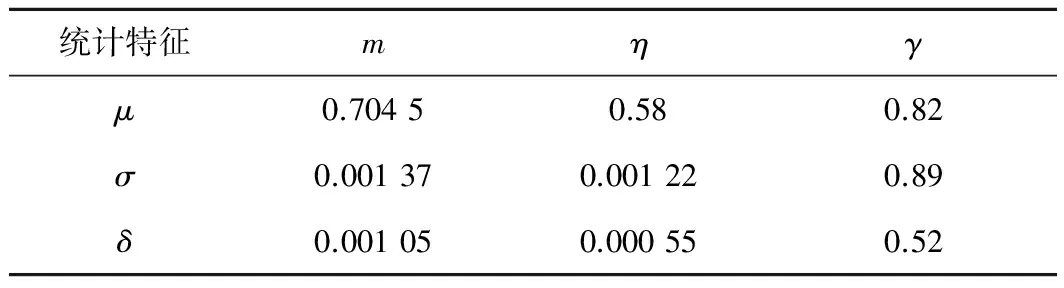
表6 喷射混凝土本构模型参数统计结果

根据表6的分析结果，即可得到喷射混凝土的统计损伤本构模型

(16)

4.4 喷射混凝土损伤本构模型的验证

为了验证本文模型，将32个喷射混凝土试件的单轴受压应力-应变试验曲线与本文模型(均值及均值加减标准差)进行对比分析，结果表明：大多数试验结果都能落在理论模型应力应变均值曲线的1倍标准差范围内，如图3所示。考虑到32个试件数据太多，图3只列出峰值应力最大和最小的试验曲线。

由图3可知，本文的喷射混凝土损伤本构模型不仅可以反映均值本构关系，还能够定量地确定其离散范围，离散范围在结构非线性随机损伤演化分析中具有重要意义。同时，由于给出了本构关系的离散范围，故能够从机理上解释混凝土试验中不可避免的离散性的本质原因。

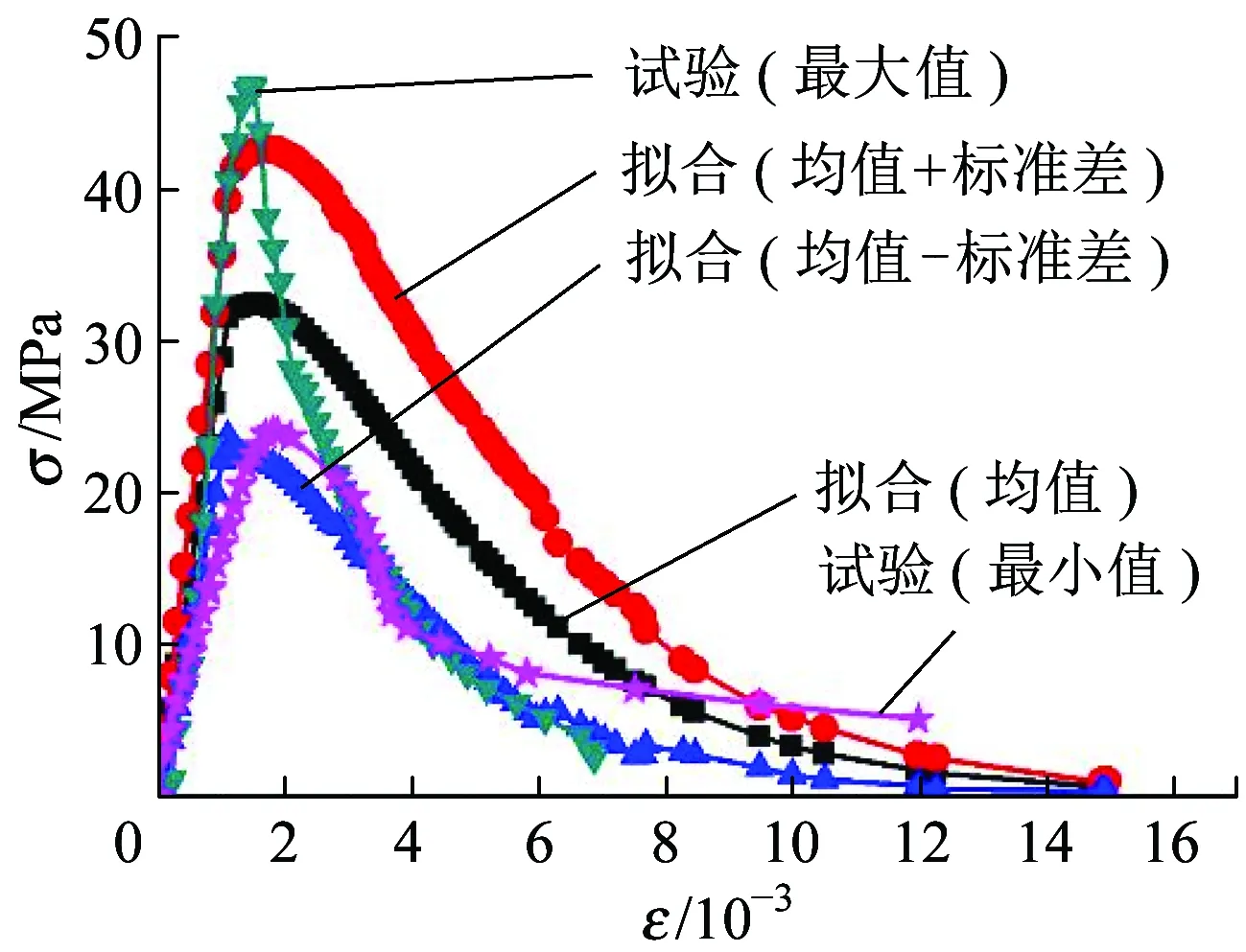
图3 试验与理论模型对比

4.5 参数m和η的物理意义

当γ=0.85、η=0.001 63时，参数m对应力-应变曲线的影响规律如图4(a)所示。由图4(a)可知，喷射混凝土的峰值应力、峰值应变随着m的增加而增大，且曲线下降段越来越陡，表明材料脆性增大。因此，参数m反映了喷射混凝土试件微元体强度分布的集中程度。当γ=0.85、m=0.9时，参数η对应力-应变曲线的影响规律如图4(b)所示。由图4(b)可知，喷射混凝土峰值应力随着η的增加而增大，η从宏观层面上反映了喷射混凝土平均强度的大小，且η对曲线下降段的软化模量影响不大。

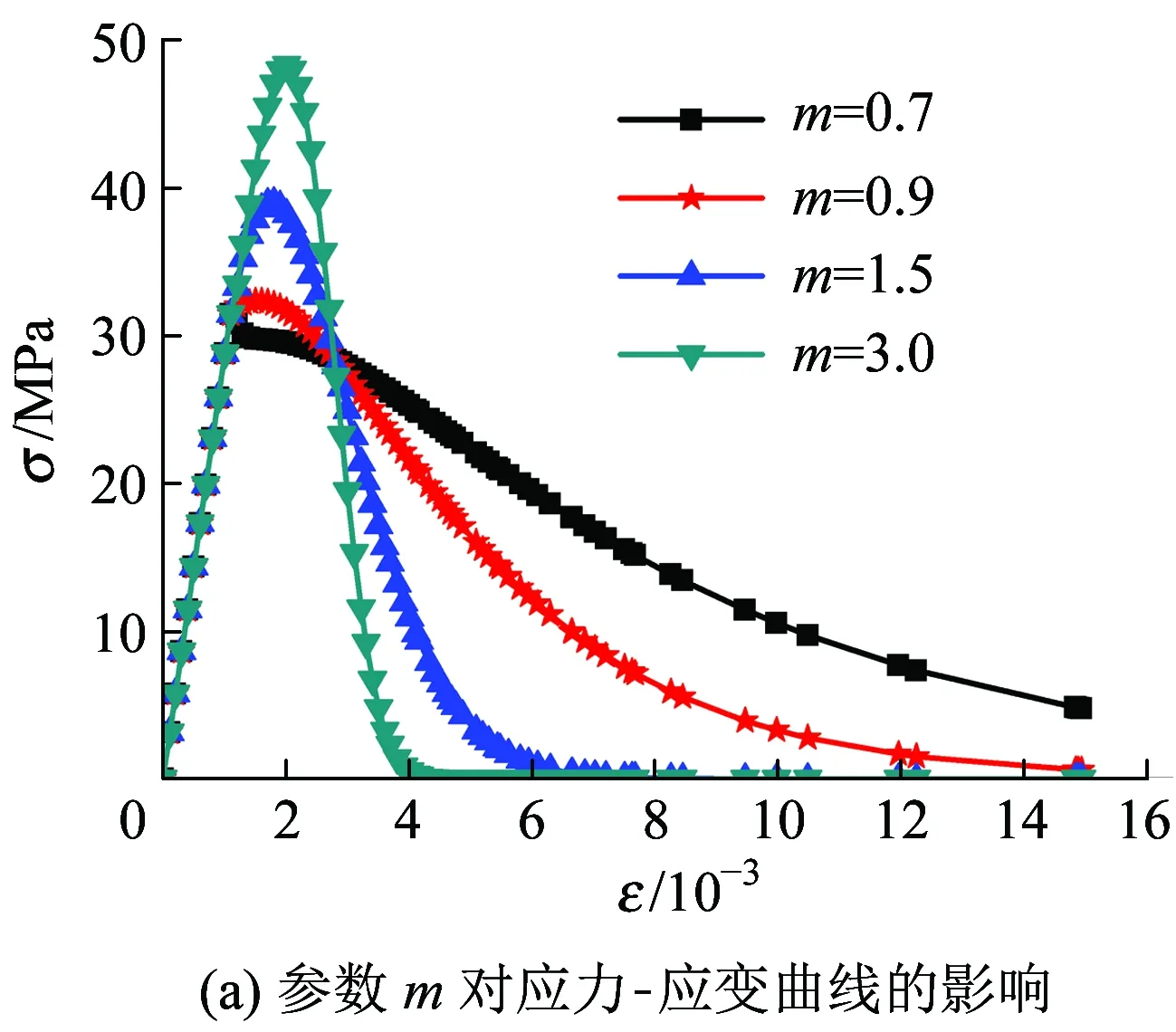
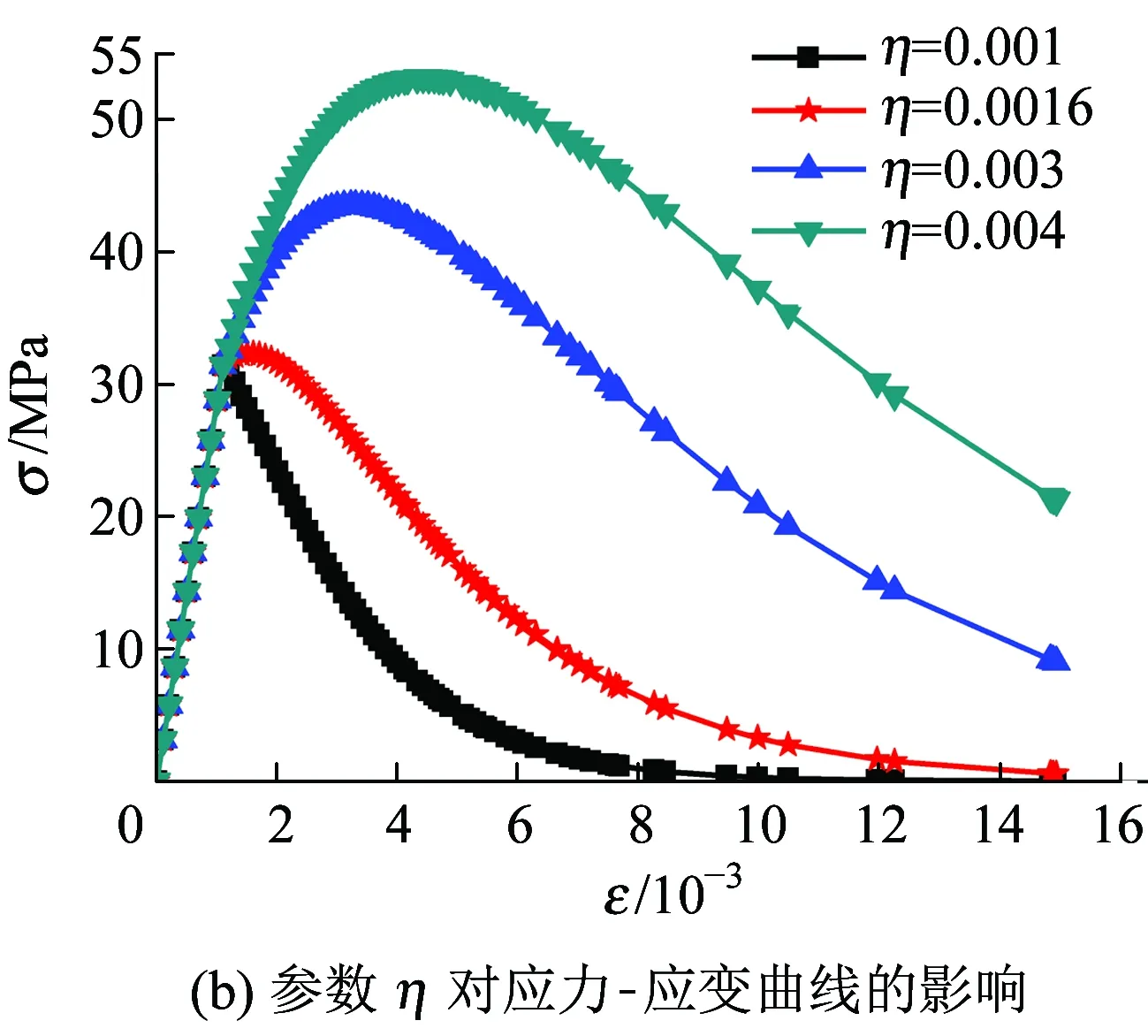
图4 参数m和η对应力-应变曲线的影响

5 算例分析

将试验数据分别带入本文模型、两参数Weibull概型分布模型及未考虑塑性变形的模型中，并与试验曲线进行比较，如图5所示。建立不同损伤阈值的D-ε曲线，分析γ值对损伤演化的影响规律，如图6所示。同时，对比分析两种不同混凝土的应力-应变曲线(图7)，建立两种不同混凝土的D-ε曲线(图8)，探讨不同施工工艺对混凝土损伤演化过程的影响机制。

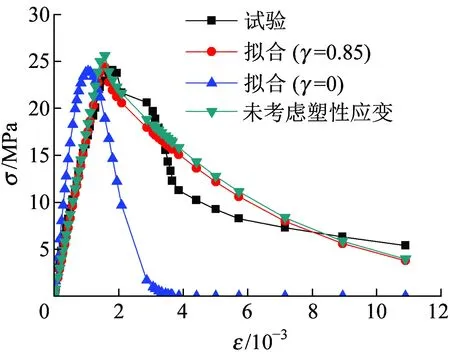
图5 试验曲线与拟合曲线对比

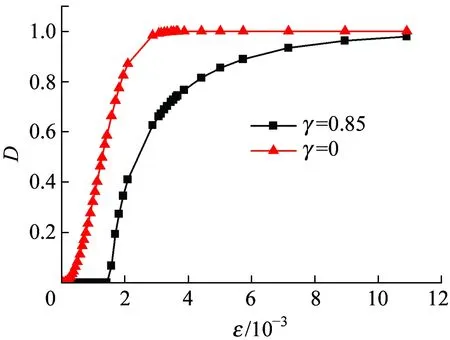
图6 不同损伤阈值的D-ε曲线

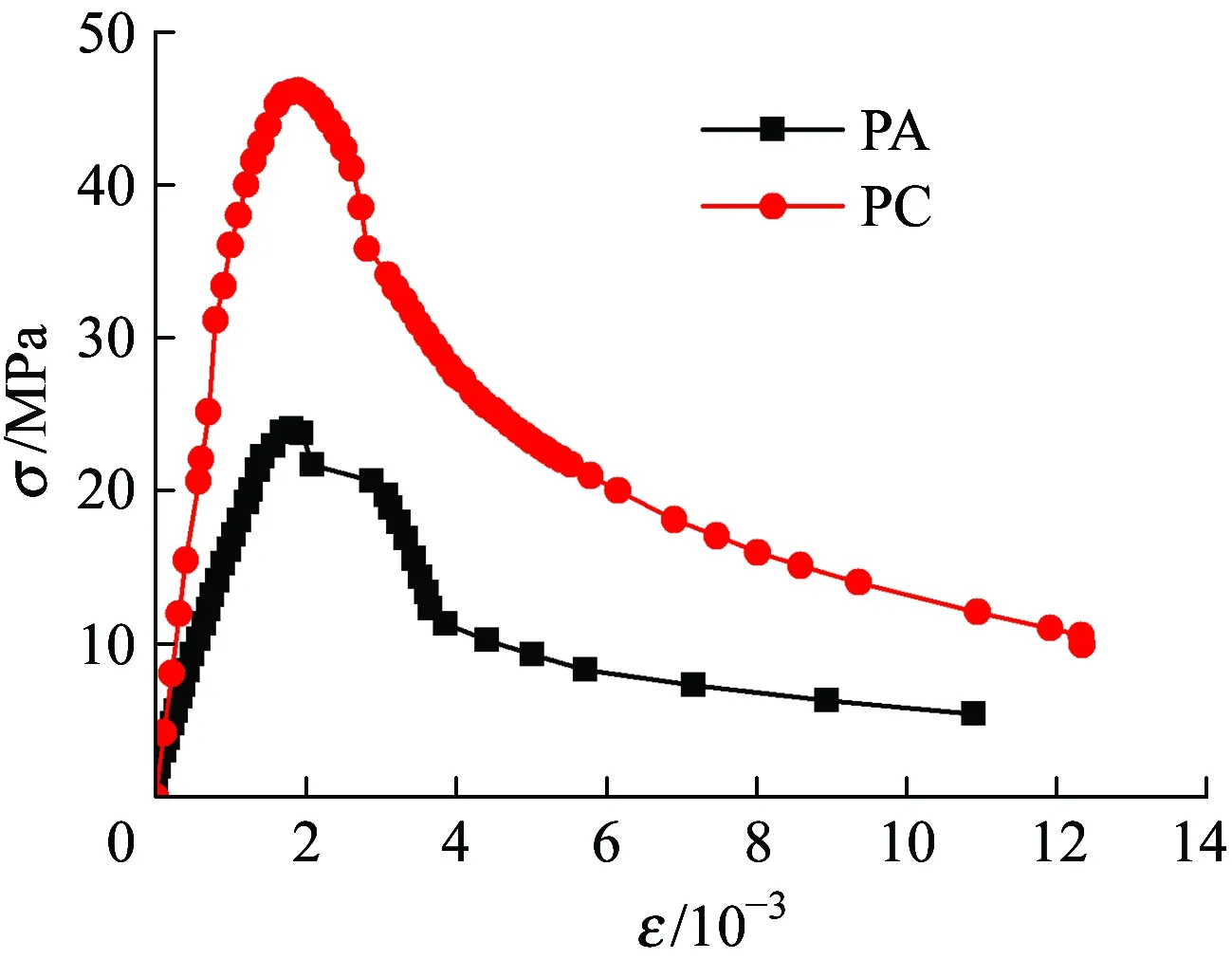
图7 不同混凝土应力-应变曲线

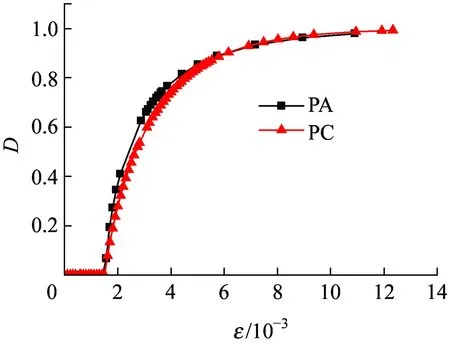
图8 不同混凝土的D-ε曲线

由图5可知，两参数模型(γ=0)上升段的斜率大于试验曲线，下降段跌落现象较严重，峰值点明显小于试验曲线，拟合效果较差；未考虑塑性应变的拟合曲线峰值应变小于试验曲线，但峰值应力大于试验曲线，出现该现象的原因是：拟合曲线所用模型在试件受载后未考虑塑性变形，而实际上混凝土的变形是由弹性变形与塑性变形两部分组成的；本文模型上升段、下降段和峰值点的大小均与试验曲线拟合较好。

由图6可知，本文模型的损伤演化方程，更好地反映了喷射混凝土受压变形过程的特点，尤其是受载初期的小变形阶段或低应力水平的损伤演化过程，即喷射混凝土在变形初期实际上处于线弹性阶段。

由图7可知，相同水胶比条件下普通混凝土的力学性能明显强于喷射混凝土，且从两种混凝土应力应变曲线围成区域的面积来看，普通混凝土的延性远好于喷射混凝土。这一点从图8中两种混凝土的损伤变量演化规律也可看出，喷射混凝土的线弹性阶段小于普通混凝土，且在产生损伤后，损伤的演化发展速率也大于普通混凝土。

6 结论

根据损伤力学、热力学中相关理论，建立了喷射混凝土单轴受压损伤本构模型。对普通混凝土、喷射混凝土单轴受压应力应变试验结果进行统计分析，确定损伤变量的概型分布及损伤演化方程，在此基础上，建立喷射混凝土统计损伤本构模型，并验证其合理性。具体结论如下：

(1)普通混凝土和喷射混凝土的损伤变量均服从Weibull分布。

(2)喷射混凝土峰值应力、峰值应变的统计均值小于普通混凝土，且延性性能也较普通混凝土差。

(3)对于喷射混凝土来说，损伤阈值γ最佳取值为0.85倍峰值应变；普通混凝土损伤阈值的最佳取值为0.8倍峰值应变。

(4)喷射混凝土损伤演化发展速率大于普通混凝土，而考虑损伤阈值的损伤演化方程能更好地反映试件受载后的变形特点。

(5)考虑塑性变形的本构模型与未考虑塑性应变的本构模型相比，可以更好且更真实地反映单轴受压条件下各种混凝土的应力应变关系。

(6)本文建立的考虑塑性变形及损伤阈值的喷射混凝土损伤本构模型可较好拟合试验应力应变曲线。

参考文献：

[1]黄平明,王达.喷射混凝土在桥梁加固中的应用[J].长安大学学报：自然科学版,2005,25(6):39-42.

HUANG Pingming, WANG Da. Application of Sprayed-concrete in Bridge Reinforcement[J]. Journal of Chang’ an University：Natural Science Edition, 2005,25(6):39-42.

[2]张仙保.锚杆喷射混凝土技术在矿山竖井工程中的应用[J].煤炭技术,2007,26(9):89-91.

ZHANG Xianbao.Application of Bolting and Shotcreting Technology in Shaft Project[J]. Coal Technology， 2007, 26 (9):89-91.

[3]肖辉椿.锚杆喷射混凝土在高位水池边坡支护中的应用[J].福建地质,2006,25(2):107-110.

XIAO Huichun. Application of the Anchor Sprayed Concrete Technique on a Side-slope Support of a High-water-level Reservoir[J]. Geology of Fujian, 2006, 25(2): 107-110.

[4]王红喜, 陈友治, 丁庆军. 喷射混凝土的现状与发展[J]. 岩土工程技术， 2004, 18(1):51-54.

WANG Hongxi, CHEN Youzhi, DING Qingjun. Modern Shotcrete Condition and Development[J]. Geotechnical Engineering Technique， 2004, 18(1):51-54.

[5]朱广兵. 喷射混凝土研究进展[J]. 混凝土， 2011(4):105-109.

ZHU Guangbing. Progress of the Research for Shotcrete[J]. Concrete， 2011(4):105-109.

[6]李杰, 张其云. 混凝土随机损伤本构关系[J]. 同济大学学报, 2001, 29(10): 1 135-1 141.

LI Jie, ZHANG Qiyun. Study of Stochastic Damage Constitutive Relationship for Concrete Material[J]. Journal of Tongji University, 2001, 29(10): 1 135-1 141.

[7]李杰. 混凝土随机损伤本构关系研究新进展[J]. 东南大学学报：自然科学版, 2002, 32(5): 750-755.

LI Jie. Recent Research Progress on the Stochastic Damage Constitutional Law of Concrete[J]. Journal of Southeast University：Natural Science Edition, 2002, 32(5): 750-755.

[8]YIP W K, KONG F K, CHAN K S, et al. A Statistical Model of Microcracking of Concrete under Uniaxial Compression[J]. Theoretical and Applied Fracture Mechanics, 1995, 22(1): 17-27.

[9]DENG J, GU D S. On a Statistical Damage Constitutive Model for Rock Materials[J]. Computers & Geosciences, 2011, 37(2): 122-128.

[10]董毓利, 樊承谋, 潘景龙. 钢纤维混凝土本构关系的研究[J]. 哈尔滨建筑工程学院, 1993, 26(2): 86-92.

DONG Yuli, FAN Chengmou, PAN Jinglong. Studies on the Constitutive Model of SFRC[J]. Journal of Harbin Architechure & Civil Engineering Institute, 1993, 26(2): 86-92.

[11]宋玉普, 赵国藩, 彭放, 等. 钢纤维混凝土内时损伤本构模型[J]. 水利学报, 1995, 26(6): 1-7.

SONG Yupu, ZHAO Guofan, PENG Fang, et al. Endochronic Damage Constitutive Model for Steel Fiber Reinforced Concrete[J]. Journal of Hydraulic Engineering, 1995, 26(6): 1-7.

[12]董毓利, 谢和平, 李世平. 砼受压损伤力学本构模型的研究[J]. 工程力学, 1996, 13(1): 44-53.

DONG Yuli, XIE Heping, LI Shiping. Damage Mechanics Constitutive Model of Concrete under Compression[J]. Engineering Mechanics, 1996, 13(1): 44-53.

[13]王胜辉, 袁勇. 喷射混凝土试验方法评述[J]. 昆明理工大学学报:理工版, 2005, 30(4):55-58.

WANG Shenghui, YUAN Yong. Reviews on Testing Methods of Shotcrete[J]. Journal of Kunming University of Science and Technology:Science and Technology, 2005, 30(4):55-58.

[14]贺少辉, 马万权, 曹德胜, 等. 隧道湿喷纤维高性能混凝土单层永久衬砌研究[J]. 岩石力学与工程学报， 2004, 23(20):3 509-3 517.

HE Shaohui, MA Wanquan, CAO Desheng, et al. Permanent Single-layer Tunnel Lining by Fibre-reinforced High Performance Shotcrete and Wet-mix Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20):3 509-3 517.

[15]樊文熙, 张长海, 郑永保. 高性能喷射混凝土的耐久性研究[J]. 煤炭学报, 2000, 25(4):366-368.

FAN Wenxi, ZHANG Changhai, ZHENG Yongbao. Study of Durability of High Performance Shotcrete[J]. Journal of China Coal Society, 2000, 25(4):366-368.

[16]KRAJCINOVIC D, SILVA M A G. Statistical Aspects of the Continuous Damage Theory[J]. International Journal of Solids and Structure, 1982, 18(7): 551-562.

[17]范镜泓，高艺晖. 非线性连续介质力学基础[M]. 重庆: 重庆大学出版社, 1987.

[18]谷耀新. 三参数威布尔分布参数估计方法[J]. 沈阳工业学院学报, 1997, 16(4): 53-56.

GU Yaoxin. The Estimation Method for Three Parameters of Weibull Distribution[J]. Journal of Shenyang Institute of Technology, 1997, 16(4): 53-56.

[19]吴建营. 基于损伤能释放率的混凝土弹塑性损伤本构模型及其在结构非线性分析中的应用[D]. 上海: 同济大学, 2004.