基于概率需求的高速铁路无砟轨道板温度荷载取值研究Ⅱ：温度梯度作用

欧祖敏， 孙 璐

（1.广东珠三角城际轨道交通有限公司，广东 广州 510308；2.东南大学 交通学院，江苏 南京 210096；3.美国普林斯顿大学 工程与应用科学学院，美国 新泽西州 08544）

无砟轨道结构因整体性好、变形小、维修工作量少等优点而被广泛应用于高速铁路［1］，但曝露于大气环境下的混凝土无砟轨道板易受外界环境温度作用影响而产生温度梯度和翘曲变形，当轨道板温度变形受到约束后产生温度应力［2-4］。选取合理的无砟轨道板温度梯度是准确计算温度翘曲应力的前提，而我国无砟轨道设计规范仅推荐常用的温度梯度为45℃／m［5］。刘学毅等［6］参照我国公路路面工程中关于温度梯度标准值的成果提出3种地区最大正负温度梯度的建议值，但该推荐温度梯度为公路路面工程采用值，对高速铁路无砟轨道的适用性仍需证明。最近的研究表明，现场实测得到的轨道板温度梯度远远超过45℃／m［7-8］，对常用温度梯度统一取45℃／m仍需更多工程实际验证。因此，有必要对无砟轨道板温度梯度的取值做进一步的研究，选取更合理的温度梯度荷载作用。

本文结合无砟轨道温度场的研究成果，利用主要城市的气象资料计算得到轨道板多年的温度梯度荷载历程，分析城市所在地轨道板温度梯度分布规律，然后根据文献［9-10］有关可变作用及取值的相关规定，对无砟轨道板的温度梯度荷载的取值进行研究，为无砟轨道板的设计和应用提供参考依据。

1 无砟轨道板温度梯度

1.1 无砟轨道板温度场方程

研究表明，无砟轨道结构内的温度分布与其表面温度的变化密切相关［11］。近似均质的混凝土无砟轨道板每日的温度场为［11-12］

式中：T（z，t）为轨道板z处在时刻t的温度；¯Ta，d为轨道板表面气温日均值，℃；~Ta，d为轨道板表面气温日幅值，℃；z为轨道板厚度（深度）方向的坐标；ζ＝为材料的导温系数，一般在0.001 86～0.003 82间，本文取a＝0.003，m2／h；ω为角频率，取ω为时间，h。t＝0为当天早上的（6＋t）0时，t0为太阳辐射最大值出现时与气温最高值出现时的差值所引起的轨道结构表面温度峰值出现时间相位修正值为白天考虑太阳辐射引起的轨道板表面等效温度日幅值，℃

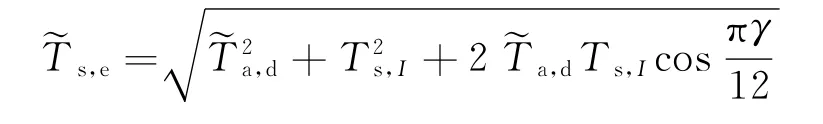
其中，Ts，I为太阳辐射在轨道结构表面产生当量温度的最大值为太阳辐射吸收系数，对水泥混凝土表面as＝0.4～0.7，本文取0.4（对光滑、浅色表面取小值）；Id为轨道板表面（水平面）日太阳辐射照度（强度），W／m2；hy为轨道板表面换热系数，hy＝ar＋acv，可取长波热辐射系数ar＝4.15，W／（m2·K）；acv为流换热系数，当风速v＜5 m／s时，acv＝6＋4·v，当风速v≥5 m／s时，acv＝7.41·v0.78，本文以日平均风速近似计算acv，W／（m2·K）；td为日照时间，h；γ为最大太阳辐射时（太阳时正午12：00）与最高气温出现时的差值加1，如1 d的最高气温出现在14：00，则γ＝3 h；相关的历史气象资料由国家气象局提供。

1.2 轨道板温度梯度日最值

混凝土板的温度可分解为均匀温度、线性温差（温度梯度）及非线性温差3部分［13］，其非线性部分仅对板产生自平衡应力而不影响结构整体平衡，参考文献［10］对普通尺寸梁板可仅考虑均匀温度荷载和线性温度梯度荷载，对轨道板可仅计算其均匀温度荷载和温度梯度荷载。由轨道结构温度场方程可知，轨道板每日的温度梯度具有周期性，可用分段函数表示为

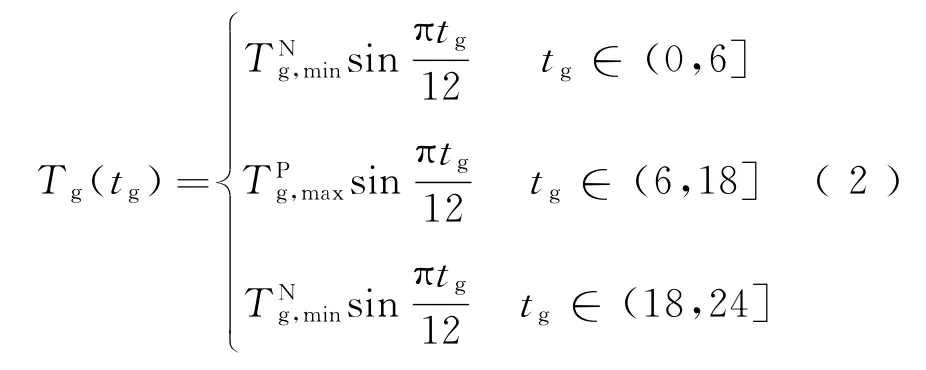
式中：Tg（tg）为轨道板在tg时刻的温度梯度值，tg＝t0当tg＝0为早上时，θq，l＝arctan分 别 为 轨 道 板 正 温度梯度日最大值、负温度梯度日最小值，℃／m。对负温度梯度取绝对值，则将要取值的负温度梯度日最小值转变为取负温度梯度绝对值的最大值，为避免混淆，本文后续统称正（负）温度梯度日最大（小）值为正、负温度梯度日最大值。轨道板正负温度梯度日最大（小）值为

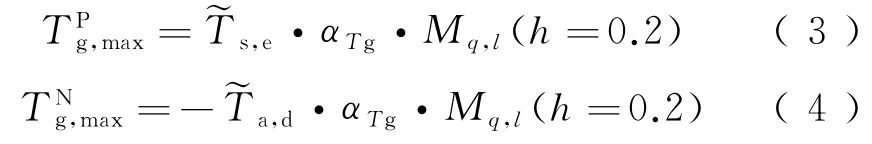
式中：Mq，l（h）为轨道板厚h的温度梯度变化系数

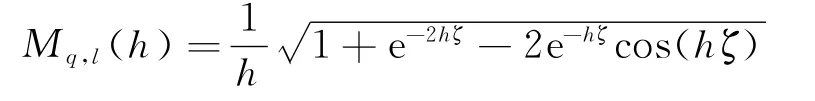
其中，Mq，l（h＝0.2）为轨道板厚度为h＝0.2 m的温度梯度变化系数；αTg为温度梯度板厚修正系数

由式（2）可知，仅用温度梯度日最大值即可表达轨道板每日的温度梯度荷载特征，本文仅研究轨道板温度梯度日最大值荷载的取值。由式（3）、式（4）可知，轨道板温度梯度的大小与板厚有关，随板厚的增大而减小，为减少计算工作量，仅对0.2 m厚度的轨道板温度梯度荷载进行研究，其他板厚的温度梯度可用表1的修正系数αTg修正。

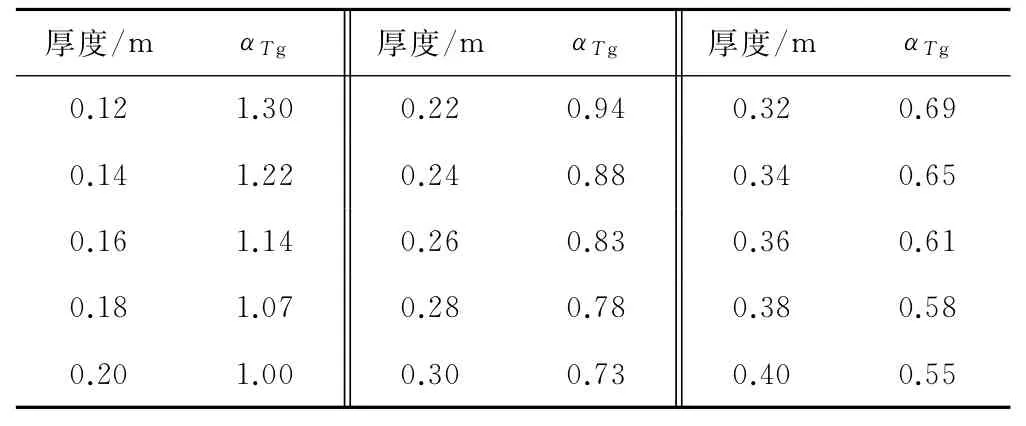
表1 轨道板温度梯度板厚修正系数αTg

2 轨道板温度梯度荷载概率模型

轨道板温度梯度日最值荷载为受外界环境温度变化产生的可变作用，属于自然作用的范畴，具有随机特性，采用随机过程模型描述较为切合实际［12］。在描述无砟轨道板的温度日最值荷载时，假定任意时点荷载记为Q，将无砟轨道的温度梯度日最值荷载模型化为随机过程｛ Q（t），t∈ ［0，T］｝，然后根据荷载随时间变化的样本函数或已有的荷载分布特征，可以确定设计基准期T内的温度梯度日最大值荷载的极大值Qmax（min）T，g。平稳二项随机过程模型是主要模型之一，参考其原理并根据温度梯度日最值的特征，可给出温度梯度日最大值（正温度梯度日最大值、负温度梯度日最小值的绝对值）的极大值概率模型［15-16］为

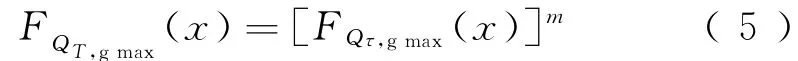
式（5）关于温度梯度日最大值的概率极值模型中，只要确定温度梯度日最值的时段概率分布函数，可求得设计基准期内温度梯度日最值荷载的极值概率分布函数，然后取某个分位值确定设计基准期内温度梯度日最值的极大值QT，gmax（min）。对轨道板温度梯度日最值的年分布，其时段长度为τ＝1 a，对设计基准期T＝60 a的无砟轨道结构，温度梯度日最值的年极值在60 a内平均出现的次数为m＝60。

3 轨道板温度梯度日最值年分布函数

3.1 北京地区温度梯度日最值分布拟合及检验

利用北京气象站历史资料（1958—2011年），按本文温度梯度日最值式（3）和式（4）以及温度场式（1）计算得到北京地区的轨道板温度正（负）温度梯度日最大（小）值的多年数据样本，对负温度梯度日最小值取绝对值进行处理，把问题转变为对正、负温度梯度的日最大值进行分析，其频数直方图见图1。

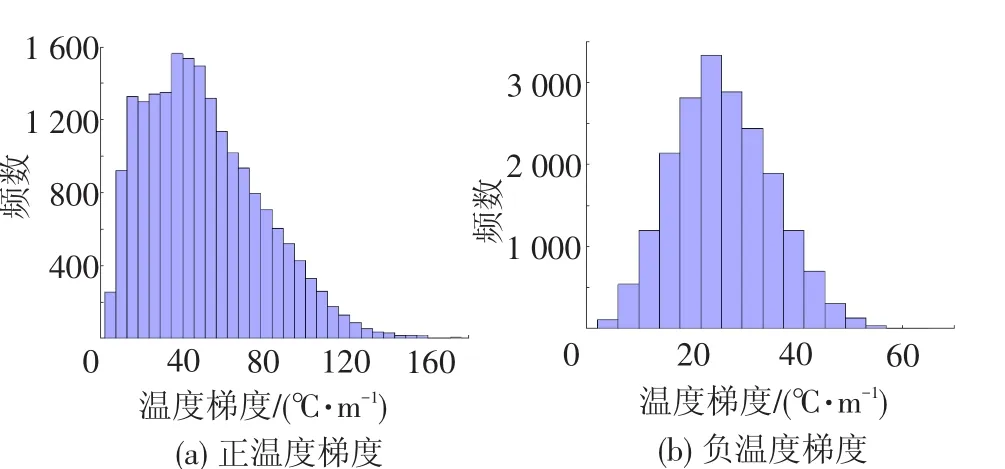
图1 北京地区1958—2011年轨道板正、负温度梯度（绝对值）日最大值频数直方图

由图1可以看出，北京地区轨道板正温度梯度日最大值呈明显的偏态，且趋于极值Ⅰ型分布、威布尔分布，而负温度梯度趋于正态分布，且呈轻微的偏态，对温度梯度日最值可以用极值Ⅰ型、威布尔、正态分布函数拟合。极值Ⅰ型分布函数为

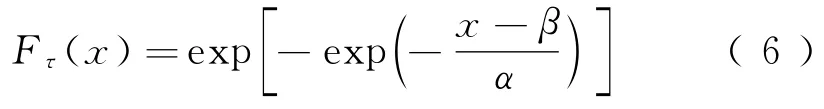
式中：α、β为极值Ⅰ型分布参数，α为比例参数，β为位置参数。

分布参数与样本平均值μ和标准差σ的关系为

两参数威布尔分布函数为

式中：γ、η为威布尔分布参数，γ为形状系数，η为尺度系数。

正态分布函数为

式中：μ、σ（σ＞0）为常数，则称X 服从参数为μ、σ2的正态分布或高斯分布。

利用北京地区1958—2011年的气象资料计算得到正、负温度梯度日最值进行统计分析，得到正态、极值型Ⅰ型、威布尔分布的参数见表2。用正态分布、极值Ⅰ型、威布尔分布概率密度曲线拟合正负温度梯度日最大值的拟合分布曲线见图2。

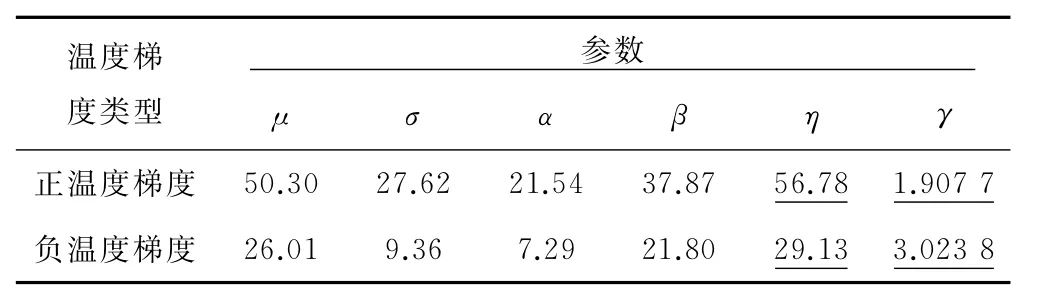
表2 北京地区1958—2011年正温度、负温度梯度作用日最值的统计参数

采用χ2拟合优度检验方法对拟合效果进行检验的结果表明，北京地区轨道板正负温度梯度日最大值的年分布都不拒绝威布尔分布。

3.2 其他地区温度梯度日最值年分布拟合及检验

采用前述方法分别计算哈尔滨、沈阳、乌鲁木齐、兰州、武汉、上海、广州、昆明等地区的轨道板正、负温度梯度日最值，然后对各城市所在地轨道板温度梯度日最值进行分布拟合，得到统计参数和检验结果见表3、表4，部分城市正、负温度梯度日最值的分布直方图及拟合效果见图3。

图2 北京地区1958—2011年轨道板正、负温度梯度日最值拟合分布曲线

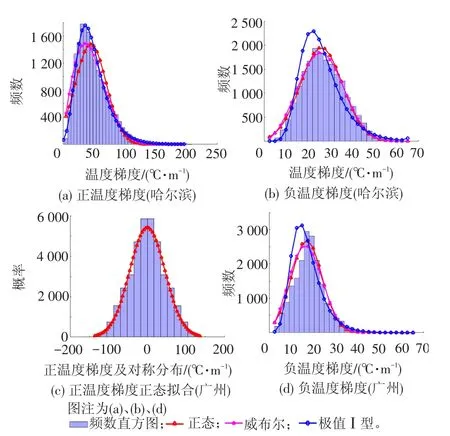
图3 哈尔滨和广州地区1961—2011年轨道板正、负温度梯度日最值频数直方图拟合曲线

对上述各个地区的轨道板温度梯度日最值进行拟合和检验时，由于各地的温度梯度日最值历年的分布变异性较大，在拟合过程中，分别采用正态、半边正态、极值Ⅰ型及威布尔4种分布函数，对负温度梯度主要采用正态分布函、极值Ⅰ型及威布尔3种分布数，结果表明所采用的函数能较好地拟合轨道板温度梯度日最值分布。

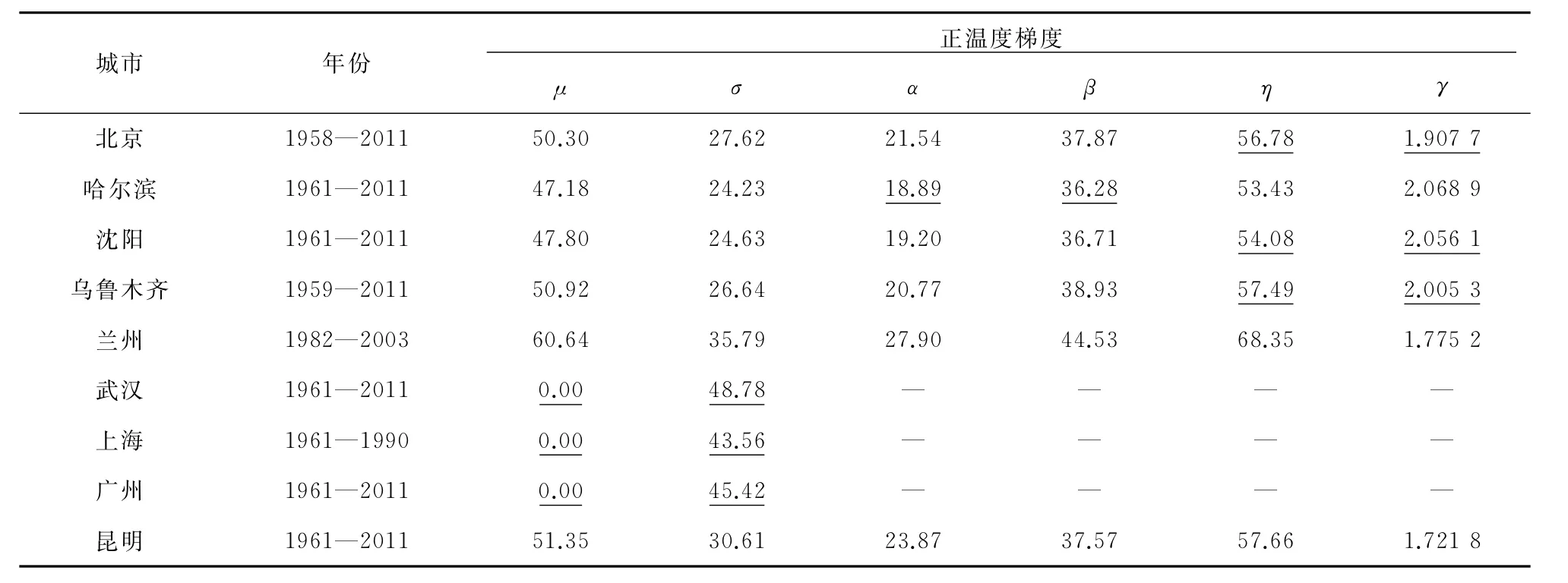
表3 部分城市历年正温度梯度作用日最值的统计参数

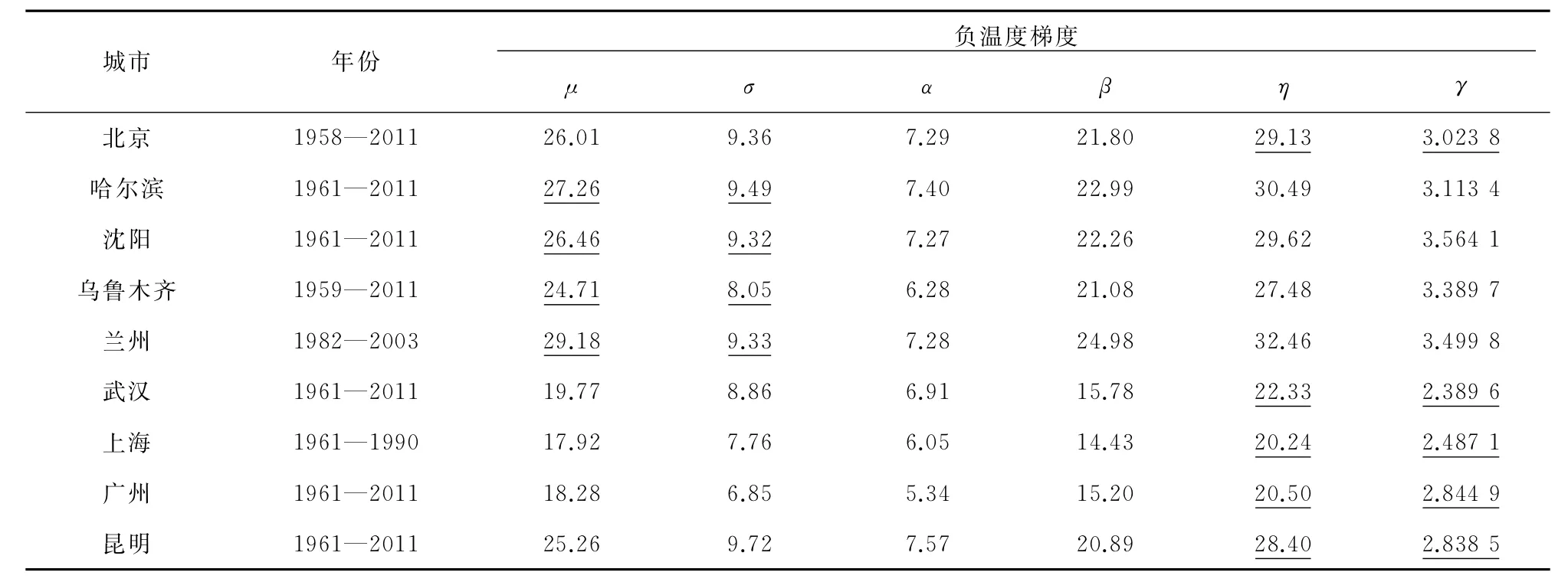
表4 部分城市历年负温度梯度作用日最值的统计参数

4 无砟轨道板温度荷载代表值

对于温度梯度的取值，我国的荷载规范没有给出应采用的设计基准期及分位值。本文分别对设计基准期为T＝50 a、T＝100 a，分位概率（保证概率）p为50%、90%、95%（相应的设计基准期荷载最大值超越概率1－p为50%、10%、5%，荷载最小值超越概率为p）的各分位值确定相应温度荷载分位值（标准值）QT。另外，考虑到温度梯度荷载为自然作用，同时采用重现期TR的形式描述温度梯度荷载，取重现期为TR为50、60、100 a，相应的年保证率1－1／TR分别为98%、98.3%、99%（对应的荷载最大值年超越概率1／TR为2%、1.7%、1%，荷载最小值年超越概率1－1／TR）。把相应的分位概率代入式（5），可得温度梯度日最值荷载分位值的表达式为

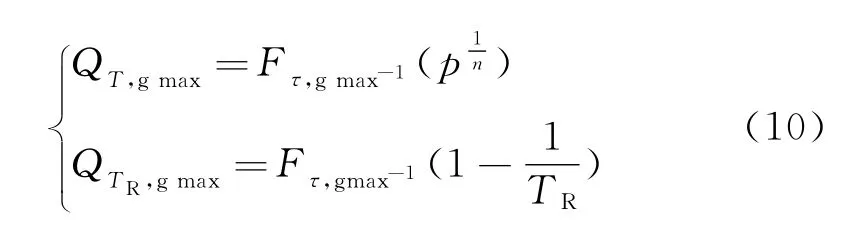
式中为正负温度梯度日最值的年概率分布函数的逆函数。

利用前述对不同地区温度梯度日最值分布拟合得到的函数及统计参数，据式（10）计算可得到部分主要城市所在地区不同设计基准期、不同分位概率（保证概率）的温度梯度日最值的分位值见表5，温度梯度日最值荷载与具有不同分位概率（也可称为保证概率，不被超越的概率或可靠性概率）的关系见图4。

由表5和图4计算结果表明，采用设计基准期定义计算得到的正负温度梯度日最值荷载（p为90%、95%的高分位值）明显高于采用重现期定义得到的温度梯度日最值荷载，这在求解其他类型的可变作用时也有类似的结果，主要是采用设计基准期与采用重现 期定义荷载标准值表达的实质不同而产生的差异［16］。

表5 不同地区不同概率的正负温度梯度日最值荷载分位值℃／m

轨道板设计所采用的正负温度梯度日最值荷载分位值（标准值），既要使轨道结构安全有一定的保证率，又要考虑经济效益而不能定得太高造成浪费，对不同地区的温度梯度日最值荷载应尽量根据其实际特征合理取值。对于温度荷载，习惯以重现期的形式描述其特征，根据前述计算结果并考虑部分城市对所在地区的代表性及工程应用的简便需求，轨道板正负温度梯度日最值荷载标准值的建议值见表6。其中，因兰州地区地理位置和特殊气候原因，计算得到的正温度梯度日最值的分位值有些偏高，如按本城市分析结果代表该区域有失偏颇，同时也不一定经济，对本区域的取值主要是参考兰州周边地区其他城市的结果确定。对不同厚度轨道板，可根据温度梯度板厚修正系数确定相应的正负温度梯度日最值荷载分位值（标准值）。

表6 不同地区正负温度梯度日最值荷载标准值建议值 ℃／m

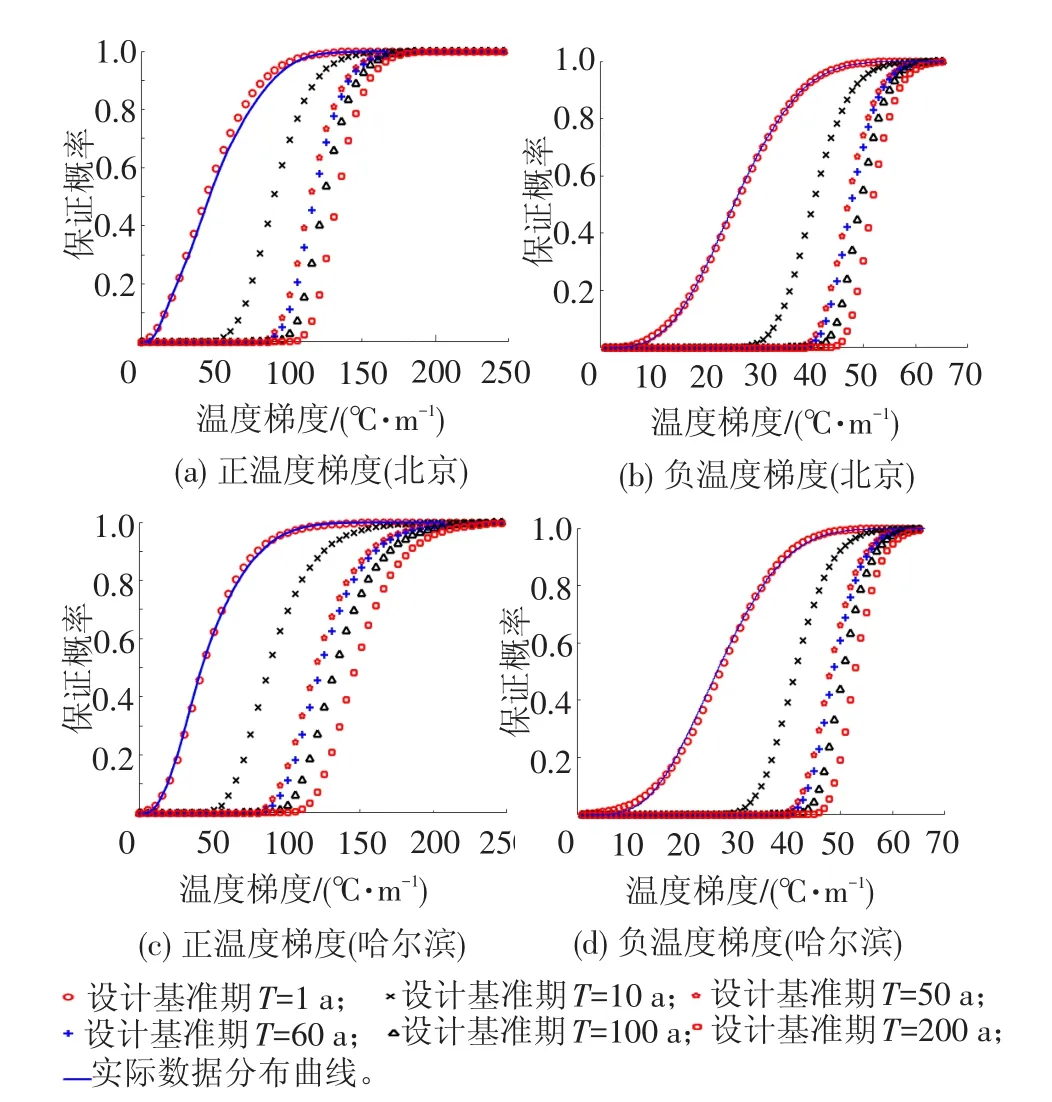
图4 不同地区不同设计基准期的正负温度梯度日最值荷载保证率概率分布曲线

5 结论

通过建立轨道板温度梯度日最值荷载的极值概率模型和统计分析温度梯度日最值的年概率分布函数，提出满足不同概率需求的轨道板温度梯度日最值荷载的取值方法，得到以下主要结论：

（1）根据温度梯度荷载的随机特性建立轨道板正负温度梯度日最值（负温度梯度绝对值最大值）的极值概率模型。

（2）利用轨道板温度场方程和城市气象资料，计算得到所在城市轨道板正温度梯度日最大值、负温度梯度日最小值绝对值。多年数据的结果表明，不同城市的轨道板正负温度梯度日最值年分布各有所不相同。对正温度梯度：哈尔滨不拒绝极值Ⅰ型分布函数，北京、沈阳、乌鲁木齐、兰州等地不拒绝威布尔分布函数，武汉、上海、广州等地不拒绝半边正态分布函数；对负温度梯度：哈尔滨、沈阳、乌鲁木齐、兰州等不拒绝正态分布函数，北京、武汉、上海、广州和昆明不拒绝威布尔分布函数。

（3）利用轨道板温度梯度日最值的年极值概率分布函数、设计基准期概率分布函数，得到温度梯度日最值荷载的常用概率分位值、不同设计基准期轨道板温度梯度日最值荷载与保证概率的关系曲线，可满足不同需求。

（4）综合考虑轨道板温度梯度日最值的分位值计算结果和主要城市对其所在地区区域代表性，提出不同地区轨道板温度梯度日最值荷载标准值的建议值。

［1］何华武.无砟轨道技术［M］.北京：中国铁道出版社，2005.

［2］LIU X，ZHAO P，DAI F.Advances in Design Theories of High-speed Railway Ballastless Tracks［J］.Journal of Modern Transportation，2011，19（3）：154-162.

［3］全毅.纵连式无砟轨道高温稳定性模型试验研究［D］.成都：西南交通大学，2017：25-39.

［4］张重王，苏成光，刘学毅，等.温度梯度与板下脱空对列车轨道系统动力响应的影响［J］.铁道学报，2017，39（4）：85-93.

TRUONG Trong Vuong，SU Chengguang，LIU Xueyi，et al.Influence of Temperature Gradient and Void Beneath Slab on Dynamic Response of High Speed Track System［J］.Journal of the China Railway Society，2017，39（4）：85-93.

［5］国家铁路局.TB 10621—2014高速铁路设计规范［S］.北京：中国铁道出版社，2014.

［6］刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法［M］.成都：西南交通大学出版社，2010：106-201.

［7］王森荣.板式无砟轨道温度应力研究［D］.成都：西南交通大学，2007：18-25.

［8］欧祖敏，孙璐，程群群.基于气象资料的无砟轨道温度场计算与分析［J］.铁道学报，2014，36（11）：106-112.

OU Zumin，SUN Lu，CHENG Qunqun.Analysis on Temperature Field of Ballastless Track Structure Based on Meteorological Data［J］.Journal of the China Railway Society，2014，36（11）：106-112.

［9］中华人民共和国住房和城乡建设部.GB 50153—2008工程结构可靠性设计统一标准［S］.北京：中国建筑工业出版社，2008.

［10］中华人民共和国住房和城乡建设部.GB 50009—2012建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012.

［11］欧祖敏，孙璐，程群群.高速铁路无砟轨道温度场简化计算方法［J］.浙江大学学报：工学版，2015，49（3）：482-487.

OU Zumin，SUN Lu，CHENG Qunqun.Simplified Calculation of Temperature Field in High-speed Railway Ballastless Track Structure［J］.Journal of Zhejiang University：Engineering Science，2015，49（3）：482-487.

［12］欧祖敏，孙璐，周杰，等.基于概率需求的高速铁路无砟轨道板温度荷载取值研究Ⅰ：轴向均匀温度作用［J］.铁道学报，2016，38（2）：96-104.

OU Zumin，SUN Lu，ZHOU Jie，et al.Probability Value of Temperature Loads for Ballastless Track Slab of High Speed Railway：Axial Uniform Thermal Actions［J］.Journal of the China Railway Society，2016，38（2）：96-104.

［13］Comite Europeen De Normalisation.EN1991-1-5 Eurocode 1：Action on Structures—Part 1-5：General Actions—Thermal Actions［S］.Brussels：Rue De Stassart，2003.

［14］赵国藩，曹居易，张宽权.工程结构可靠度［M］.北京：科学出版社，2011.

［15］白国良，薛建阳，吴涛.工程荷载与可靠度设计原理［M］.北京：中国建筑工业出版社，2012.

［16］金新阳.建筑结构荷载规范理解与应用［M］.北京：中国建筑工业出版社，2013.