公铁联运网络的枢纽选址模型及算法
2016-05-08李孟良王喜富孙全欣
李孟良,王喜富,孙全欣,王 德
(1.北京交通大学 交通运输学院,北京 100044;2.铁道党校 铁路企业管理教研部,北京 100088)
公铁联运是指货物运输过程中采用公路和铁路两种运输方式相结合,将货物从供应地运送到需求地的运输组织形式,与传统单一运输方式相比,公铁联运具有全程性、通用性、简便性、代理性和协同性的特点,可以降低运输成本、节约运杂费用和提高运输服务质量[1]。公铁联运枢纽选址具有多式联运枢纽选址的特点,与单运输方式设施选址问题相比,公铁联运枢纽选址需要考虑公路与铁路运输模式选择、衔接以及中转费用等差异,由于铁路运输自身存在时刻表限制,因此在选址过程中服务时间也是一个重要考虑因素。选择公铁联运网络中重要城市节点作为枢纽,承担货物装卸、搬运、中转、仓储、换装以及信息服务等功能,经营人将分散在各区域小批量货流集中到枢纽站,组成大批货流后,通过合适的运输方式和转载工具,将货物按需分配。建立合理的货运枢纽不仅能提高整个网络服务效率,降低运输网络总成本,还可以节能减排,缓解交通压力,实现对整个运输系统的有效利用,达到更好地利用现有设施能力的目的,对交通运输方式的可持续发展具有重要意义。
国外学者对多式联运网络枢纽选址研究较多,Racunica和Wynter[2]介绍铁路网络枢纽概念,基于增加列车频率、降低人力成本和提高设备周转率建立铁路枢纽选址费用模型,通过减少决策变量,采用启发式迭代方法求解。模型局限于解决单一铁路网络枢纽选址问题,只考虑枢纽运营费用。Limbourg和Jourquin[3]研究与本文相似的公铁联运枢纽选址问题,通过优化公路枢纽位置及合理分配铁路货流降低运输费用,提出启发式方法求解,但缺少考虑枢纽选址固定成本和服务时间限制。Ishfaq和Sox[4]研究公铁联运物流网络枢纽选址和路径分配问题,模型考虑运输费用、转运成本、固定选址成本和服务时间限制,采用拉格朗日松弛和禁忌搜索算法求解模型。王雷等[5]基于Benders分解算法解决无容量限制多分配枢纽选址问题,该算法把选址问题分为枢纽选址和路径分配两个子问题进行求解,目标函数只考虑枢纽设置成本和网络运营成本,侧重介绍Benders分解算法。傅少川等[6]通过对比多分配多枢纽和单分配多枢纽轴辐式物流网络建立单一运输费用模型,得出单分配多枢纽轴辐式网络更具有现实意义,采用改进的禁忌搜索智能算法进行求解。崔小燕等[7]针对无容量限制单分配轴辐式物流网络,设计基于运输费用最小的选址模型,重点介绍蚁群求解算法,没有考虑枢纽建设固定成本和运输时间限制影响,局限于公路运输方式的选址问题。本文和以上文献都以选址费用最小为目标函数,但本文综合考虑上述文献缺失的枢纽选址影响因素。
本文主要研究公铁联运网络货运枢纽选址模型及算法设计,创新点在于:
(1)同时考虑枢纽间运输费用、枢纽固定运营成本、非枢纽之间直接运输产生的费用、枢纽处转运费用以及运输时间限制,使模型更加符合实际情况;
(2)采用改进的禁忌搜索算法求解多分配p-枢纽中位公铁联运网络枢纽选址模型。
1 问题描述
公铁联运网络枢纽选址问题对降低运输网络物流费用极具重要性[1,8],如何选择公路与铁路组成的物理网络中关键节点作为公路枢纽、铁路枢纽或者公铁联运枢纽将是本文研究的重要问题。本文研究的商品为综合类商品,没有详细区分具体类别。设计公铁联运网络图如图1所示。
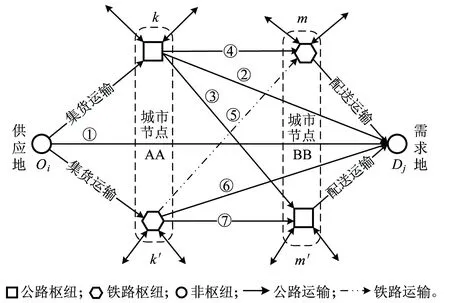
图1 公铁联运网络图
公铁联运网络包括枢纽点、非枢纽点以及具有流量和时间权重的有向连接。其中k和k′分别是城市节点AA可能建设的公路枢纽和铁路枢纽,m和m′是城市节点BB可能建设的铁路枢纽和公路枢纽,城市间都有公路和铁路连接。货物从供应地经过枢纽中转再到需求地过程中需要经过集散货运输,存在7种运输组织形式可供选择:路径①货物直接通过公路运输方式从供应地Oi运输到需求地Dj,没有经过枢纽中转;路径②和⑥货物经过单个公路枢纽k或单个铁路枢纽k′,通过公路运输,并在枢纽处进行中转;路径③货物通过两个公路枢纽k和m′,全程采用公路运输方式;路径⑤货物通过两个铁路枢纽k′和m运输,在两个铁路枢纽之间采用铁路运输方式,从供应地到第一个铁路枢纽k′以及从第二个铁路枢纽m到达需求地均采用公路运输方式;路径④货物从供应地依次通过公路枢纽k和铁路枢纽m到达需求地,路径⑦货物从供应地先后通过铁路枢纽k′和公路枢纽m′到达需求地,这两种组织形式均采用公路运输。与文献[8]相比,本文所提出的模型在目标函数选址费用方面考虑的更加全面,优越性主要体现在考虑非枢纽间直接运输费用、枢纽处转运费用以及运输时间限制方面,既有模型在这方面考虑的不够具体。
2 公铁联运网络的枢纽选址模型建立
本文考虑枢纽间运输费用、枢纽固定运营成本、非枢纽间直接运输费用、枢纽处转运费用以及运输时间限制等影响因素,建立公铁联运网络总费用最小的枢纽选址模型。模型建立需要做三个假设:
(1)假设货物由供应地到需求地至多经过两个枢纽转运;
(2)货物从供应地运输到第一个枢纽以及由最后一个枢纽配送到需求地均采用公路运输;
(3)同一城市最多只能建设一种类型的枢纽。
2.1 符号及参数
公铁联运网络枢纽选址模型参数设置为
N:城市节点数;
i:供应城市节点;
j:需求城市节点;
k,m:枢纽节点;
P:备选枢纽个数;
M:一个足够大的正数;
S:运输方式集合{0,1},s∈S,s=0表示公路运输,s=1表示铁路运输;
fij:供应城市i到需求城市j的货运量;
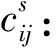
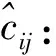
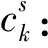
Fk:城市k选为枢纽的固定运营费用,包括人力、设备、租赁和资金占用费用等;
α:成本折扣系数,0≤α≤1,可以实现货物流在跨枢纽运输时产生的成本节约,抵消建设枢纽的固定成本投资和运营费用,给经营者带来额外收益;
βs:枢纽间运输方式为s的时间延迟因子,βs≥1,解决枢纽处中转时间对模型的影响,更符合实际情况;
C(k,m,s):货物在枢纽(k,m)间由运输方式s产生的运输成本;
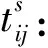
Tij:供应城市i到需求城市j的服务时间限制。
0-1决策变量:
yk:城市k是否为枢纽;
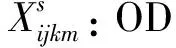
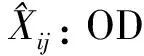
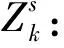
2.2 模型构建
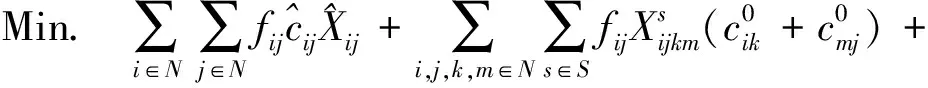
(1)
s.t.
(2)
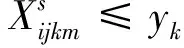
(3)
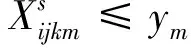
(4)
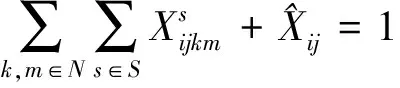
(5)
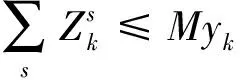
(6)
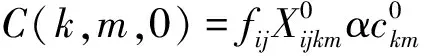
(7)
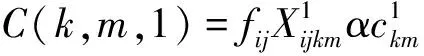
(8)
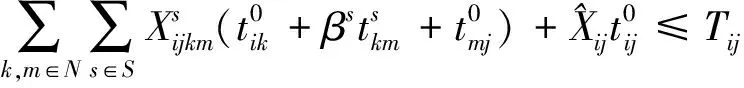
(9)
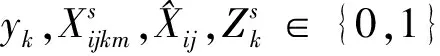
(10)
目标函数(1)以运输过程中总费用最小为目标,总费用包括第一项公路直接运输费用、第二项和第三项通过枢纽对(k,m)运输费用、第四项枢纽固定运营成本以及转运费用;式(2)建设枢纽个数为p;式(3)和式(4)表示只有节点k,m建设为枢纽时,才有基于该枢纽的运输路径选择;式(5)表示OD对之间运输模式选择约束,两者之间只能选择一种最优的运输路线;式(6)表示只有节点k选为枢纽才能选择是否需要转运;式(7)和式(8)分别表示枢纽对(k,m)由公路运输和铁路运输产生的费用成本;式(9)表示OD对之间运输时间不能大于最迟到达时间约束限制;式(10)表示决策变量为(0,1)变量。
3 模型求解算法
公铁联运网络枢纽选址问题属于NP-hard问题,文献[9]提出用禁忌搜索算法解决此类问题,并找到误差小于1%的最优解。本文采用改进的禁忌搜索(TS)算法,通过设置禁忌表来禁忌过去的操作,利用特设准则来解禁一些优良状态,在一定程度上接受劣解,使其在搜索过程中跳出局部最优解,实现全局优化。具体求解思路和求解步骤如下。
3.1 禁忌搜索算法求解思路
禁忌搜索算法求解思路:首先按照随机方法产生一个初始解yk作为当前解,采用邻域优先的搜索方法,将枢纽和非枢纽之间成对交换作为邻域搜索方向,并在当前解的邻域中搜索若干个解,取其中最优解作为新的当前解。使用禁忌表记录已搜索的局部最优解的历史信息,从而避免迂回搜索。为了能逃离局部最优解,算法必须接受劣解,一旦接受劣解,迭代就可能陷入循环。算法将最近接受的一些移动放在禁忌表中,在以后的迭代中加以禁止,以此避免循环,即只有不在禁忌表中的较好解,才被接受作为下一次迭代的初始解。随着迭代的进行,禁忌表不断更新,经过给定迭代次数后,最早进入禁忌表的移动就从禁忌表中解禁退出。当随机产生初始解次数达到给定的次数后,禁忌搜索终止,输出最优解。
禁忌搜索算法参数设定
(1)解的表示
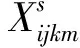
(2)初始解产生
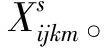
(3)邻域构建及候选解集选择
通过枢纽节点和非枢纽节点之间成对交换作为邻域搜索方向,根据评价函数的优劣构造候选解,本文评价函数越小,候选解替代当前解的概率越大。
(4)评价函数构建
本文将模型中目标函数作为评价函数,评价值minZ越小越好。
(5)禁忌表和禁忌长度
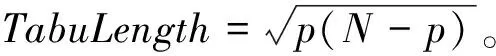
(6)特赦及停止准则
特设准则:采用评价函数值的特赦准则,候选解中所有解为禁忌解时,则解禁最好解。
停止准则:采用最大迭代次数Nmaxiter=10n。
3.2 禁忌搜索算法求解步骤
禁忌搜索算法包括全局多样化搜索和区域强化搜索两阶段[10]。第一阶段确定枢纽位置,第二阶段进行网络路径分配。具体求解步骤如下:
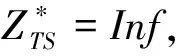
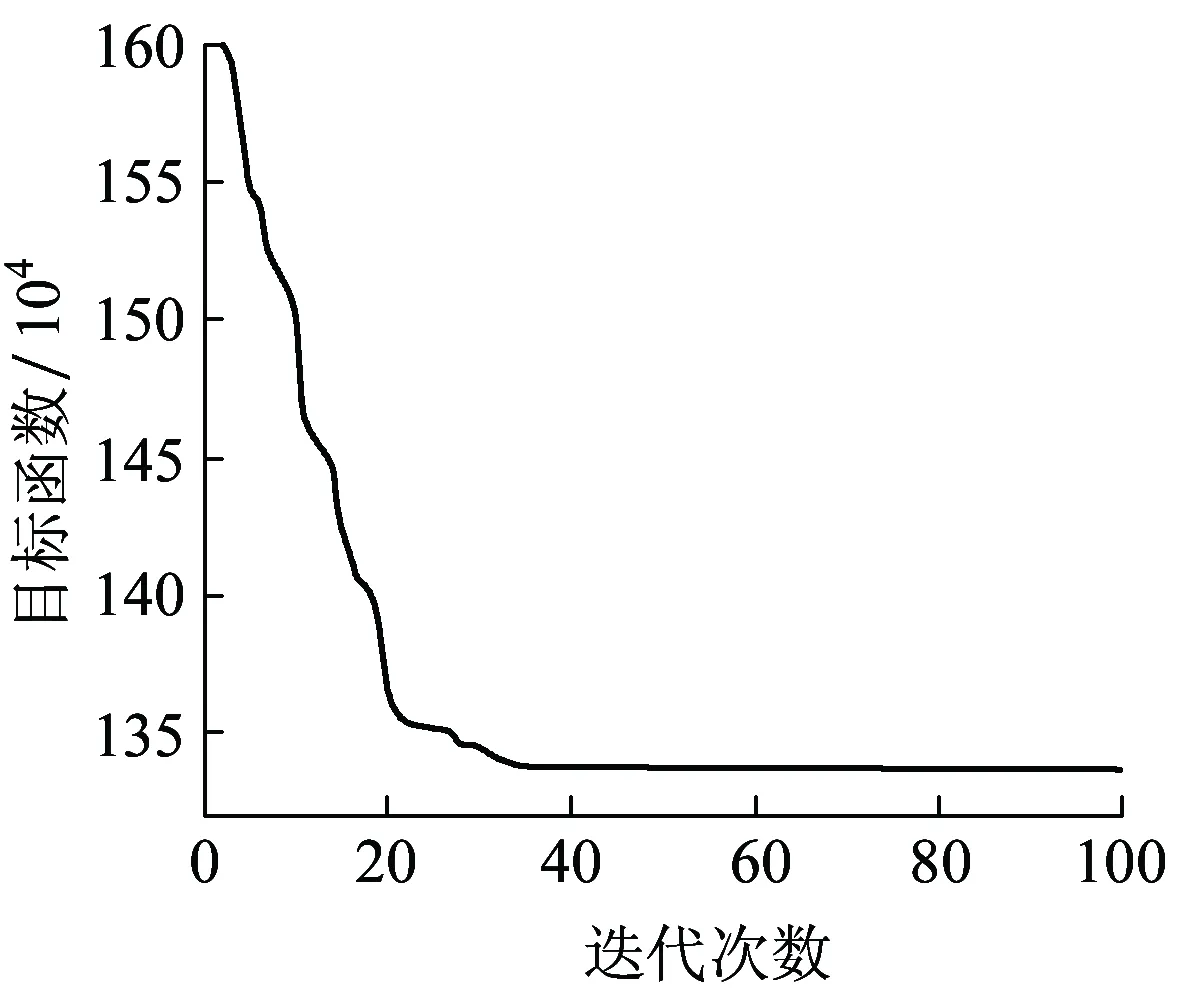
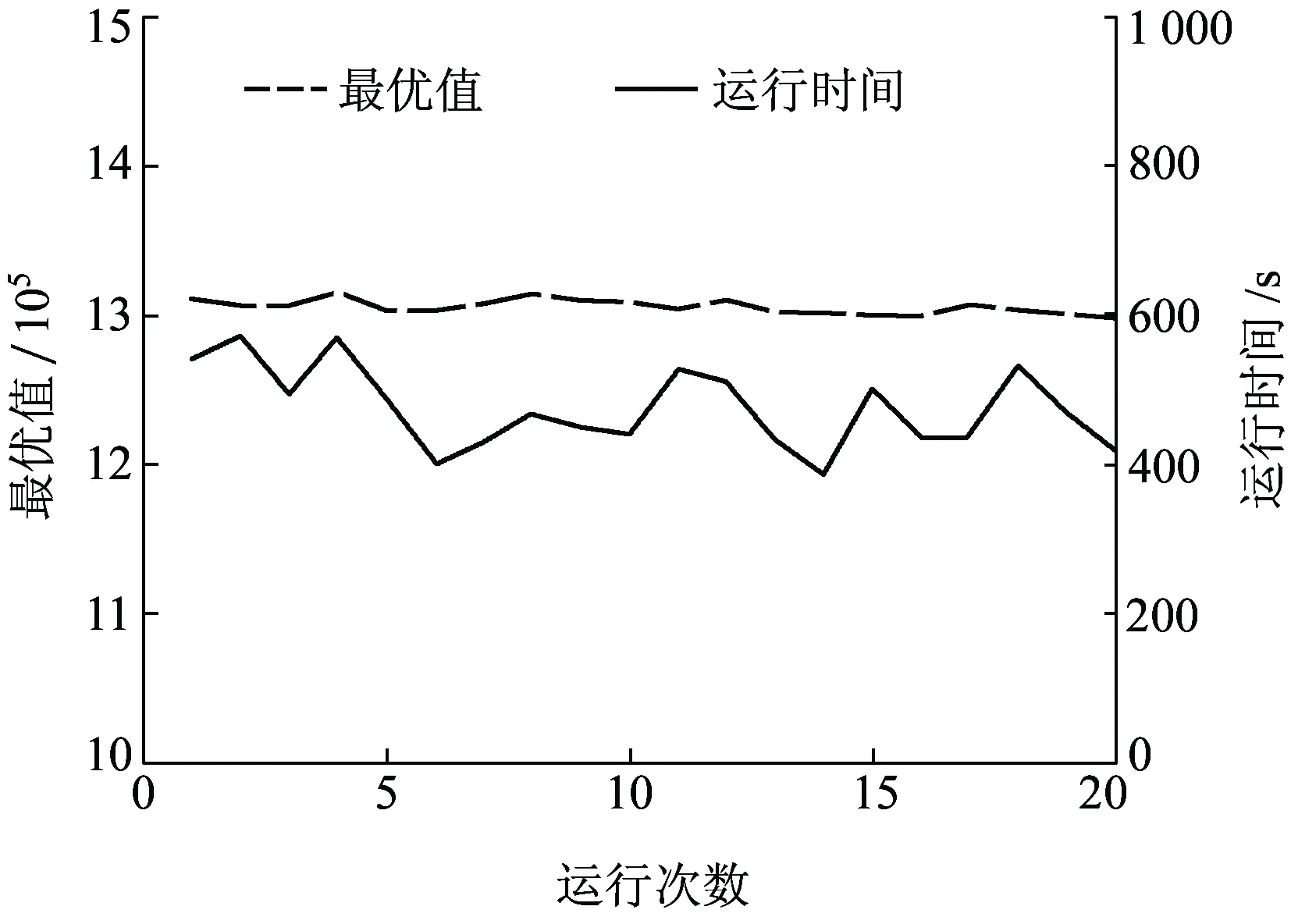
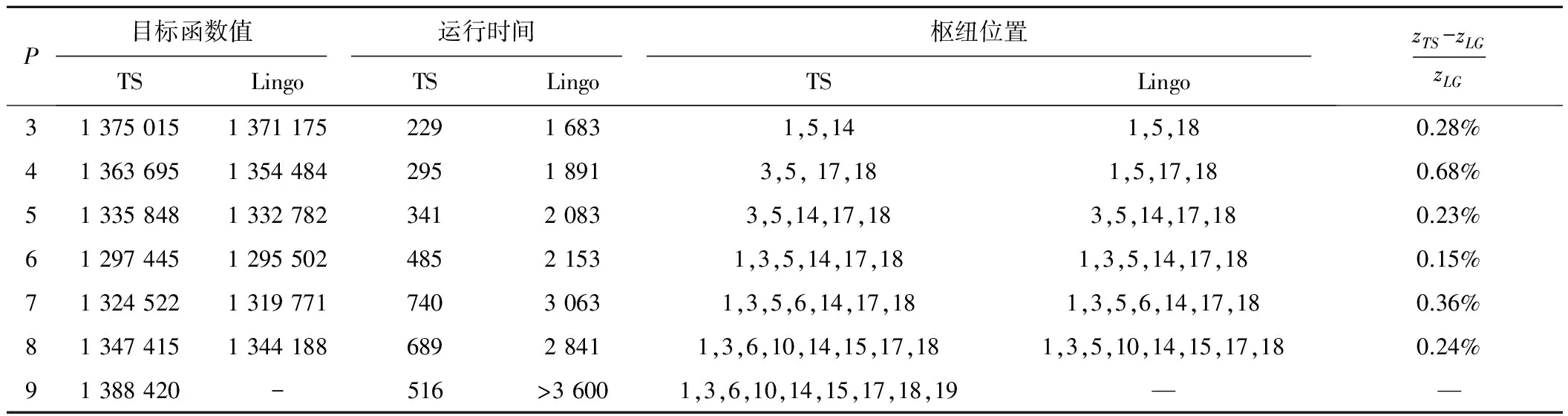
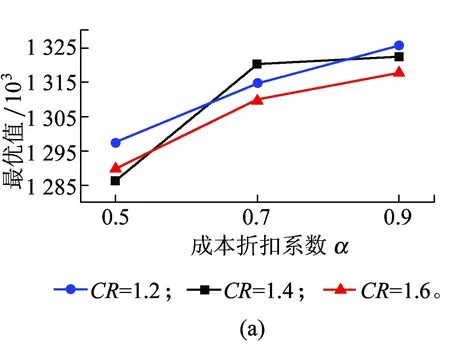
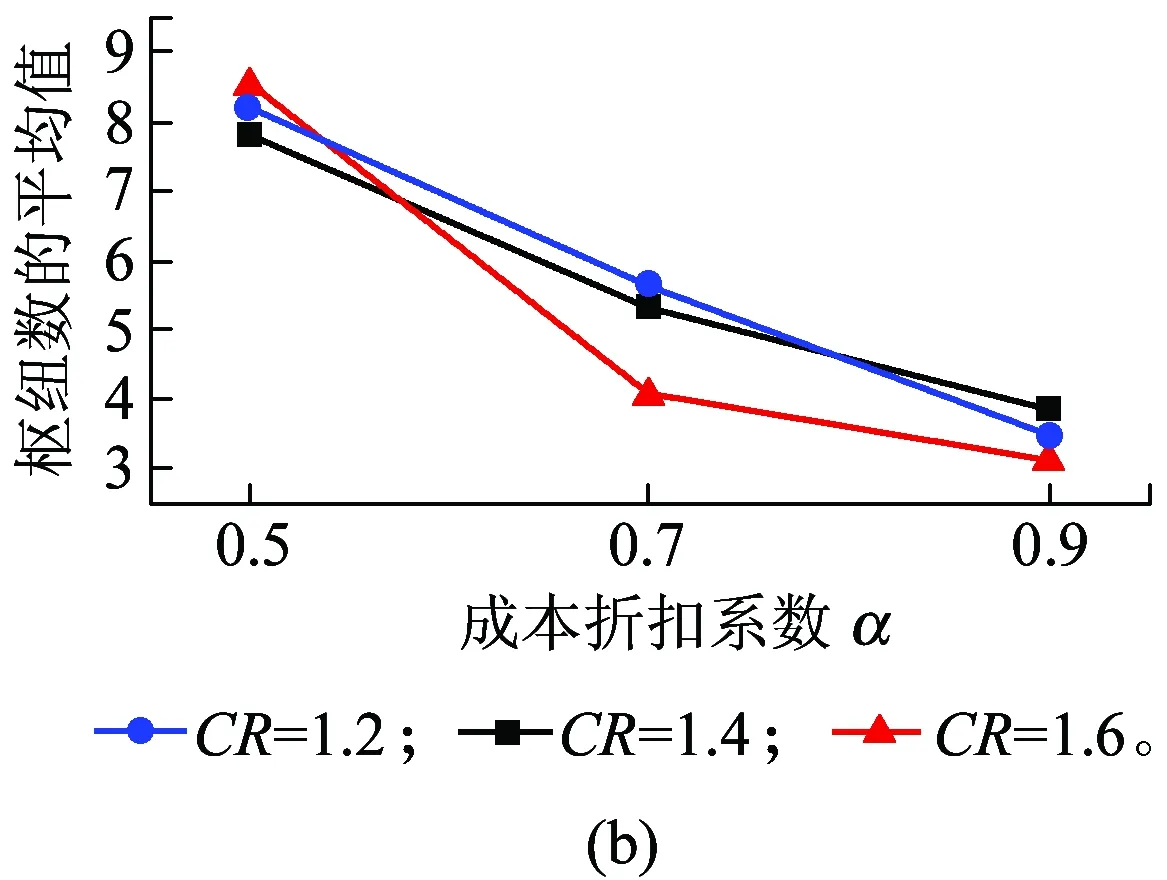
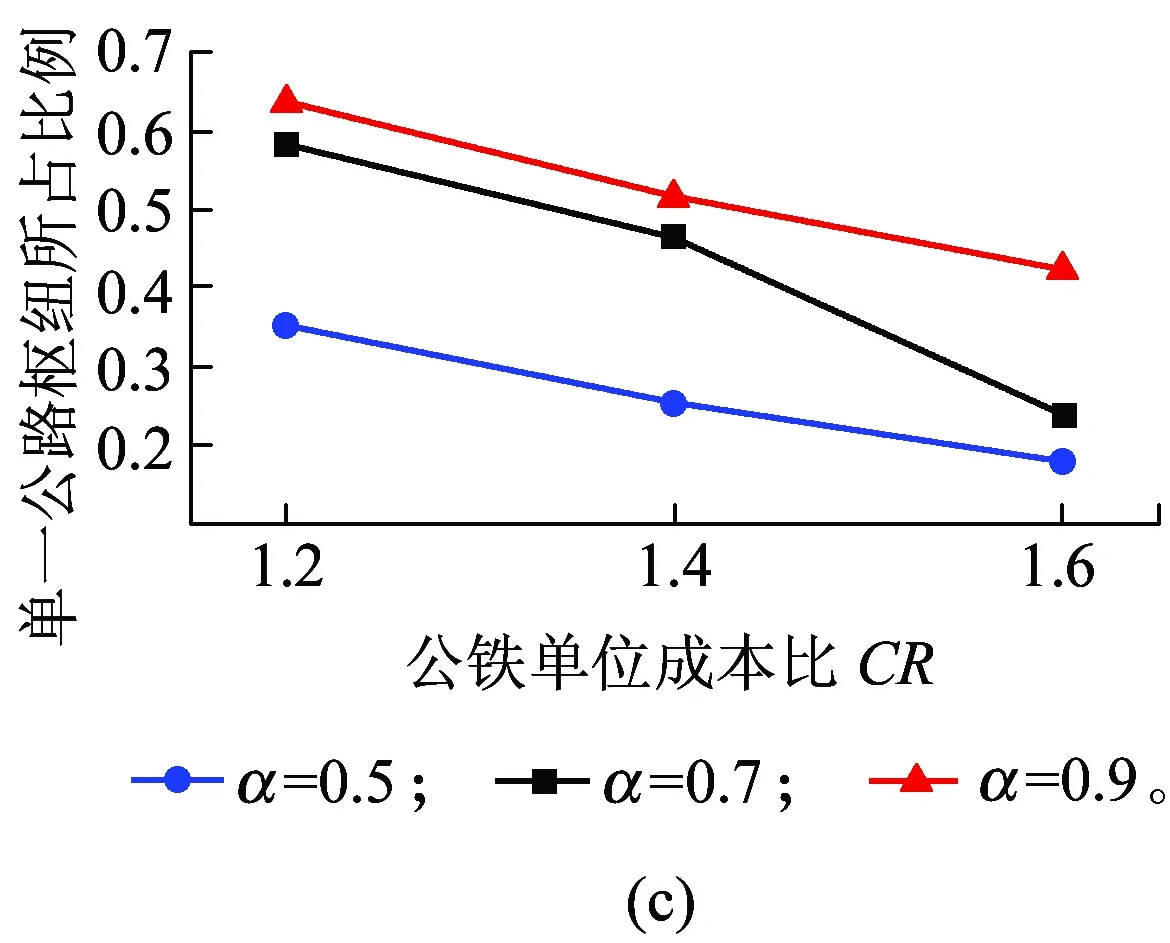
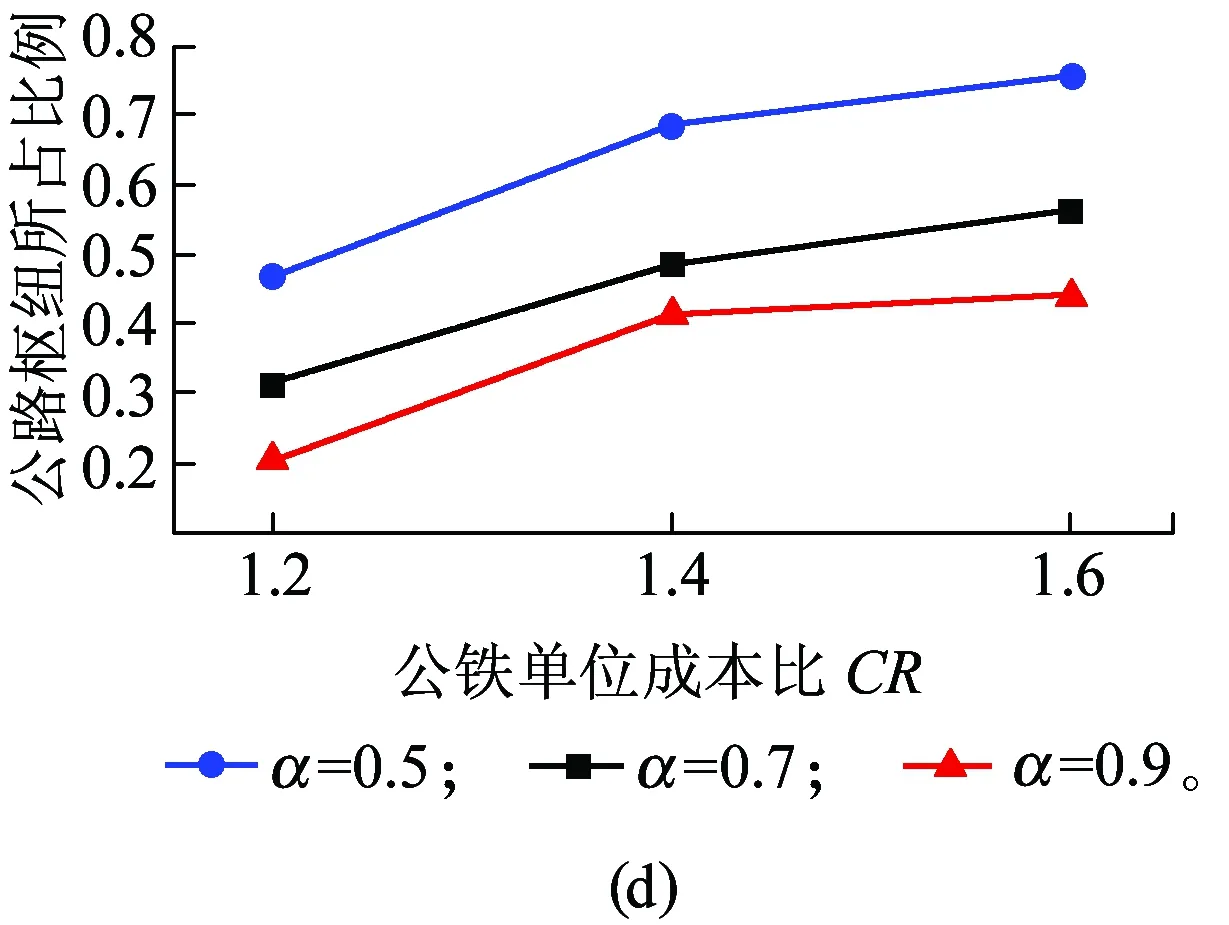
步骤2判断第一阶段Rcount 步骤4禁忌表中除新加入OD对外,原有OD对(q,r)进行length(q,r)=length(q,r)-1操作,如果length(q,r)=0,则(q,r)离开禁忌表。 步骤5判断所有可能移动是否在禁忌表中,如果满足,进一步判断是否满足特赦准则,本文采用的特设准则为候选解的适配值优于历史最优值,否则更新Tabu_list、当前解;如果节点频率大于给定的阈值(Freqlimit),则在初始解中踢出该节点,置空Tabu_list,并更新当前解、初始解;如果nodefrequency≤Freqlimit,直接置空Tabulist,令当前解=初始解,返回步骤1。 步骤6当随机产生初始解次数Rcount达到Mcount后,禁忌搜索终止,输出最优解 本文基于Rardin and Uzsoy[11]中算例构建,数据满足公路单位货运成本高于铁路,铁路枢纽中转时间大于公路枢纽中转时间。选取20个城市节点作为算例,具体空间分布情况如图2所示。 图2 20个城市空间分布 表1 城市节点之间的货流量 表2 影响因子设计[12] (1)模型有效性验证 为了验证禁忌搜索算法求解模型的有效性,影响因子分别取表2集合中第一个元素,通过MATLAB编程将程序运行20次,选取最优一次计算过程,其收敛情况如图3所示。 图3 禁忌搜索算法收敛优化曲线 图3中取最大迭代次数为100次,收敛曲线在35代附近开始趋于收敛,说明禁忌搜索算法初始收敛快,后期精度改善相对缓慢。最优解和运行时间如图4所示。 图4 最优解与运行时间对比 由图4可以分析出目标函数最优值集中在1 297 445,没有出现明显波动,说明模型的正确性和稳定性;求解时间分布在[384.6 s,570.9 s]之间,平均时间为474.1 s,说明禁忌搜索算法可以在较短的时间得到最优解。禁忌搜索算法与Lingo分支定界算法性能比较见表3。 表3 TS与Lingo结果对比 通过数据分析得到TS最优值为1 295 502,与Lingo分支定界精确解仅相差0.15%,TS与Lingo求解间隙最大为0.68%,最小为0.15%,但TS求最优解的时间仅是Lingo的22.5%,两种求解方法得到最佳枢纽位置均为[1,3,5,14,17,18]。但Lingo在求解大规模网络时存在数据容易溢出、运行时间较长的局限性,例如当P=9时,Lingo的运行时间超过3 600 s,仍未得到满意的解,而禁忌搜索算法完全可以在较短时间内找到满意解,并且具有较强的稳定性和收敛能力。 (2)成本折扣系数和公铁单位成本比对选址结果影响分析 公铁联运网络中,当货物流的规模扩大时,运输总成本随着运量的增加呈现非线性缓慢增加,单位运输成本随之降低。通过成本折扣系数α可以实现货物流在跨枢纽运输时产生的成本节约,抵消建设枢纽的固定成本投资和运营费用,给经营者带来额外收益,成本折扣系数和公铁单位成本比的大小直接影响选址结果。成本折扣系数α={0.5,0.7,0.9}和公铁单位运输成本CR={1.2,1.4,1.6}情况下对选址结果的影响如图5所示。 图5 成本折扣系数和公铁单位成本比对选址结果的影响 图5(a)表示成本折扣系数与公铁单位成本比对目标函数最优值的影响。在CR一定情况下,最优值随α增加而增大,这是因为跨枢纽城市间运输成本折扣系数越大,所需要运输费用越高,α=1取极值情况下,枢纽间运输成本相当于直接运输,没有产生折扣,此时运输费用最大;图5(b)表明枢纽间折扣系数α越大,公铁联运最佳枢纽平均数越小,当公铁单位成本比为1.2时,折扣系数α由0.5增加到0.9,最佳枢纽平均值则由8.2降低到3.5,减少了57.3%,当公铁单位成本比为1.6时,最佳枢纽的平均值则由8.5减少到3.1,降低了65.9%,说明成本折扣系数对最佳枢纽平均值的影响程度远大于公铁单位成本比对最佳枢纽平均值的影响;图5(c)表明公铁单位成本比和成本折扣系数对单一公路枢纽所占比例的影响趋势与图5(d)相反;图5(d)表明在α一定情况下,公铁联运枢纽所占比例随着公铁单位成本比的增加而增大,在CR一定情况下,公铁联运枢纽所占比例随着成本折扣系数的增大而减小,进一步证明结果符合实际情况。 综上所述,公铁联运网络中铁路运输成本低所带来的效益完全可以被成本折扣系数的规模效应所抵消,因此,在公铁联运网络中,选择合适的枢纽位置及枢纽类型将会减少整个运输过程中的总费用。 本文考虑枢纽间运输费用、枢纽固定运营成本、非枢纽间直接运输费用、枢纽处转运费用以及运输时间限制等多种影响因素,建立无容量限制多分配p-枢纽中位选址模型,运用改进的禁忌搜索元启发式算法进行求解,研究公铁联运枢纽选址问题,并通过算例分析及算法比较验证本文所提模型和算法可以有效用来解决公铁联运网络的枢纽选址问题。本文所提方法对公铁联运枢纽选址具有一定借鉴意义,同时还可以扩展到公路水路联运、铁路水路联运、铁路公路水路联运和公路航班联运,以及在考虑枢纽容量限制情况下如何设计模型更加符合实际情况。 参考文献: [1]石小法. 货运交通系统[M]. 上海:同济大学出版社, 2013:23-30. [2]RACUNICA I, WYNTER L. Optimal Location of Intermodal Freight Hubs[J]. Transportation Research Part B, 2005, 39(5): 453-477. [3]LIMBOURG S. Jourquin B Optimal Rail-road Container Terminal Locations on the European Network[J]. Transportation Research E, 2009, 45(4):551-563. [4]RAFAY Ishfaq, CHARLES R Sox.Hub Location-allocation in Intermodal Logistic Networks[J]. European Journal of Operational Research, 2011, 210:213-230. [5]王雷,吴薇薇.Benders分解算法在多分配枢纽选址问题的应用[J].信息技术,2012,5(7):1-10. WANG Lei, WU Weiwei. Benders Decomposition Algorithm for Multi-distribution Hub Location Problem[J].Information Technology, 2012,5(7):1-10. [6]傅少川,胡梦飞,唐方成.禁忌搜索算法在单分配多枢纽轴辐式物流网络中的应用[J].中国管理科学, 2012, 20(3): 145-151. FU Shaochuan, HU Mengfei, TANG Fangcheng. The Optimization of Hub and Spoke Logistics Network Design Based on Tabu Search Algorithm[J]. Chinese Journal of Management Science,2012, 20(3): 145-151. [7]崔小燕,李旭宏,毛海军,等. 无容量约束单分配轴-辐式物流网络设计[J]. 交通运输系统工程与信息, 2010, 10(5): 175-181. CUI Xiaoyan, LI Xuhong, MAO Haijun, et al. Design of Uncapacitated Hub-and-Spoke Logistics Networks with Single Allocation [J]. Journal of Transportation Systems Engineering and Information Technology, 2010,10(5):175-181. [8]RAFAY Ishfaq, CHARLES R Sox. Intermodal Logistics: The Interplay of Financial, Operational and Service Issues [J]. Transportation Research Part E, 2010, 46: 926-949. [9]SKORIN Kapov D,SKORIN Kapov J,O'Kelly ME. Tight Linear Programming Relaxations of Uncapacitated P-hub Median Problems[J]. European Journal of Operational Research, 1996, 94(3): 582-593. [10]汪定伟,王俊伟,王洪峰,等. 智能优化方法[M]. 北京:高等教育出版社,2007:81-110. [11]RARDIN R L, UZSOY R. Experimental Evaluation of Heuristic Optimization Algorithms: A tutorial[J]. Journal of Heuristics, 2001, 7: 261-304. [12]SLACK, B. Intermodal Transportation in North America and the Development of Inland Load Centers[J]. Professional Geographer, 1990, 42(1): 72-83.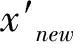
4 算例分析
4.1 数据描述
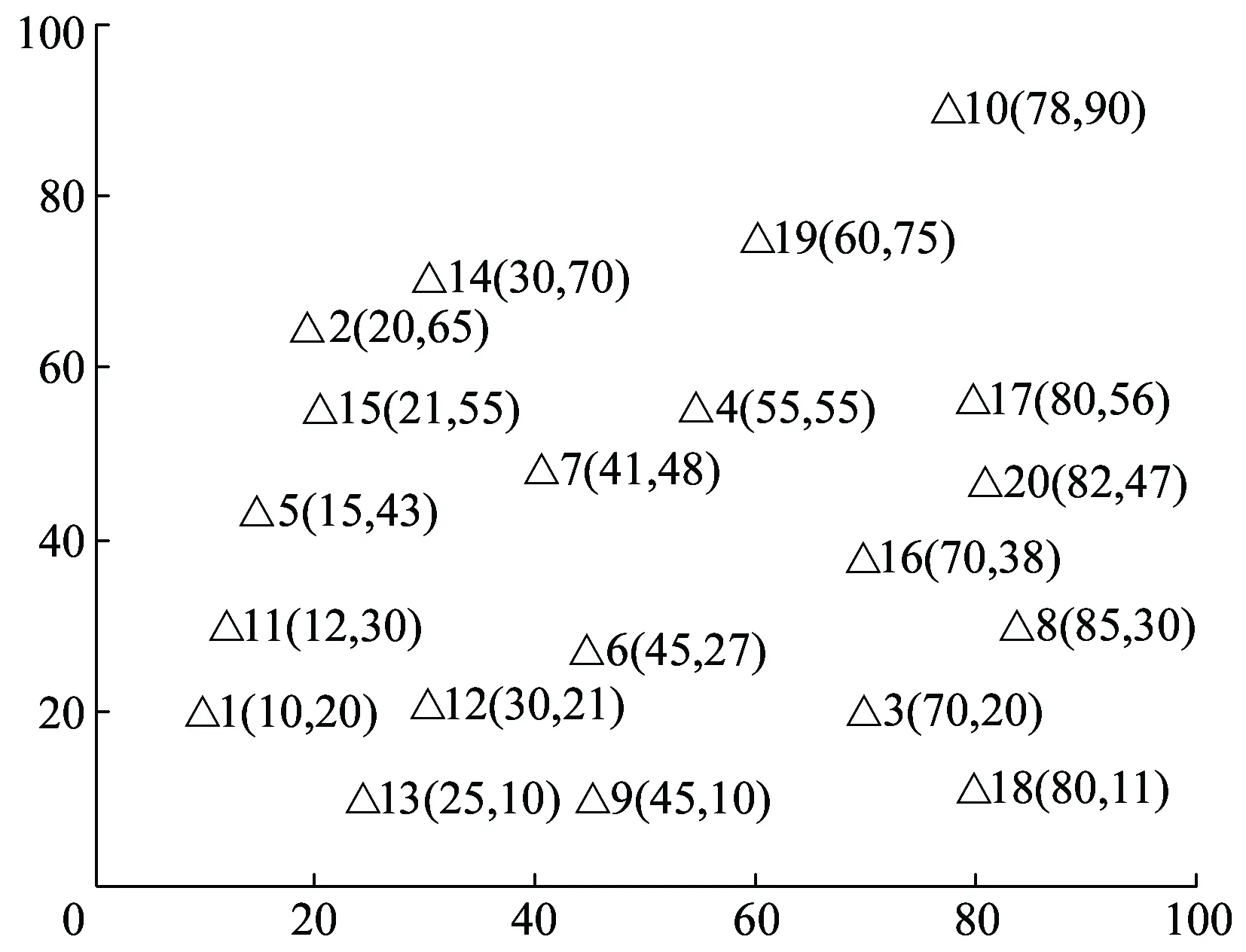
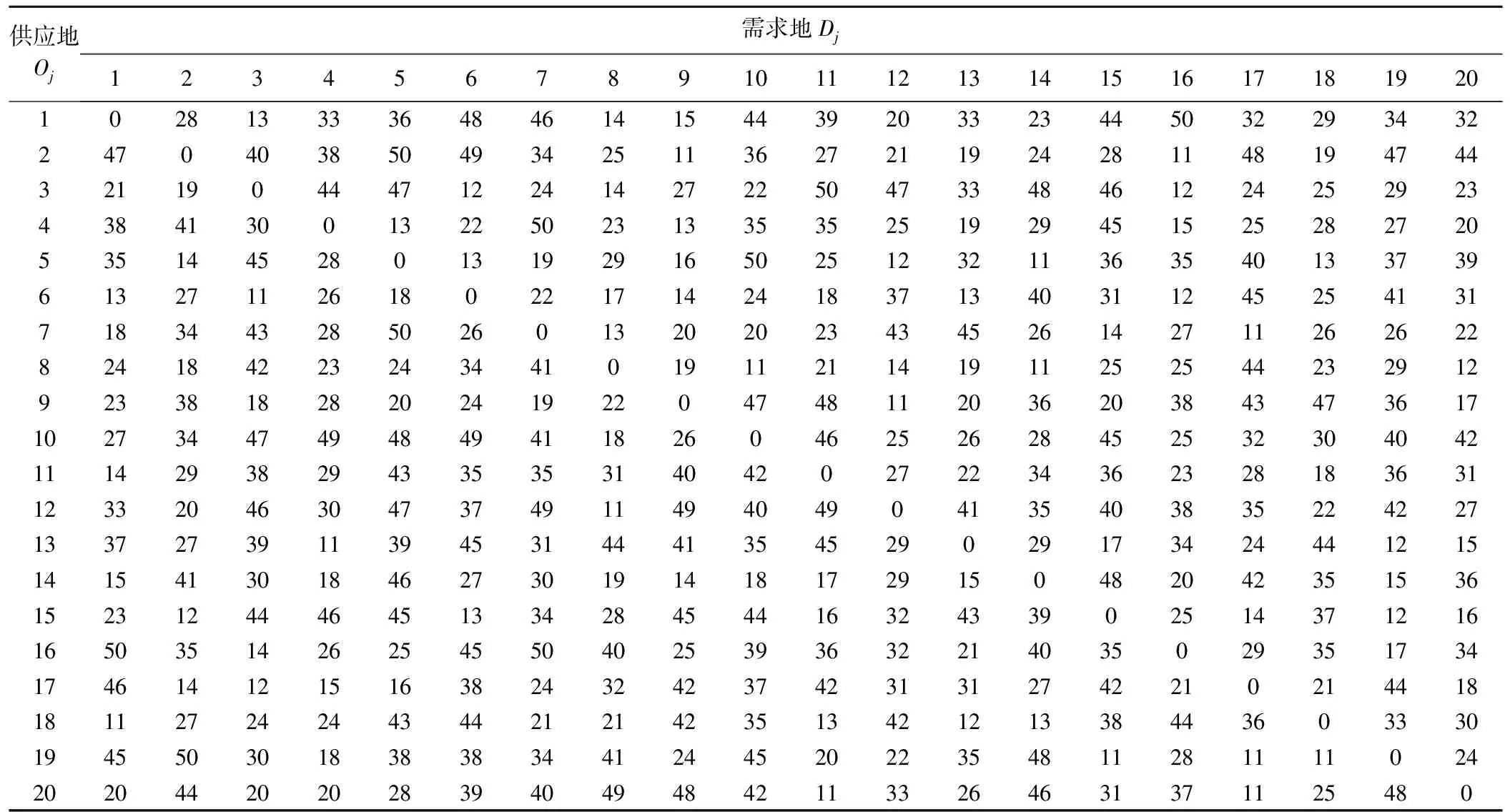

4.2 结果与分析
5 结束语
