压剪复合型弹性车轮踏面磨耗行为研究

丁军君，杨 阳，李 芾

(西南交通大学 机械工程学院， 四川 成都 610031)

城轨车辆由于要穿过居民区，其轮轨噪声的控制对沿线居住环境至关重要。当采用弹性车轮后，城轨车辆的轮轨噪声可以比传统刚性车轮降低5～8 dB，对高频(大于1 000 Hz)噪声甚至可以降低15～30 dB[1]。文献[2]基于数学模型对相同轴重条件下的弹性车轮和刚性车轮垂向动作用力进行研究，结果表明弹性车轮轮轨垂向作用力较刚性车轮最多可降低70%。为了研究弹性车轮扁疤对道床振动和噪声的影响，文献[3]建立了弹性车轮的噪声预测模型和轮轨动态作用模型。文献[4]基于有限元-边界元法建立了车轮声辐射计算模型，分析弹性车轮的降噪特性，结果表明弹性车轮在宽频带内可以明显降低振动声辐射，弹性车轮的总辐射声功率较传统刚性车轮降低6 dB (A)。

对弹性车轮的研究主要集中在噪声和轮轨作用力上[5]，目前尚没有相关文献报道弹性车轮磨耗后的踏面形状特征及弹性车轮的磨耗寿命。本文以压剪复合型弹性车轮为例，根据车辆踏面磨耗仿真原理，研究弹性车轮和相同条件下刚性车轮的磨耗行为，并分析弹性车轮橡胶元件参数对车轮磨耗的影响。

1 压剪复合型弹性车轮动力学模型

弹性车轮有多种型式，主要的结构型式有剪切型、压缩型和压剪复合型。由于压剪复合型弹性车轮可以对轮毂和轮芯之间的径向和轴向刚度进行合理匹配，保证车轮具有良好的动力学性能，因此广泛运用于地铁和城轨车辆中，其结构如图1所示。

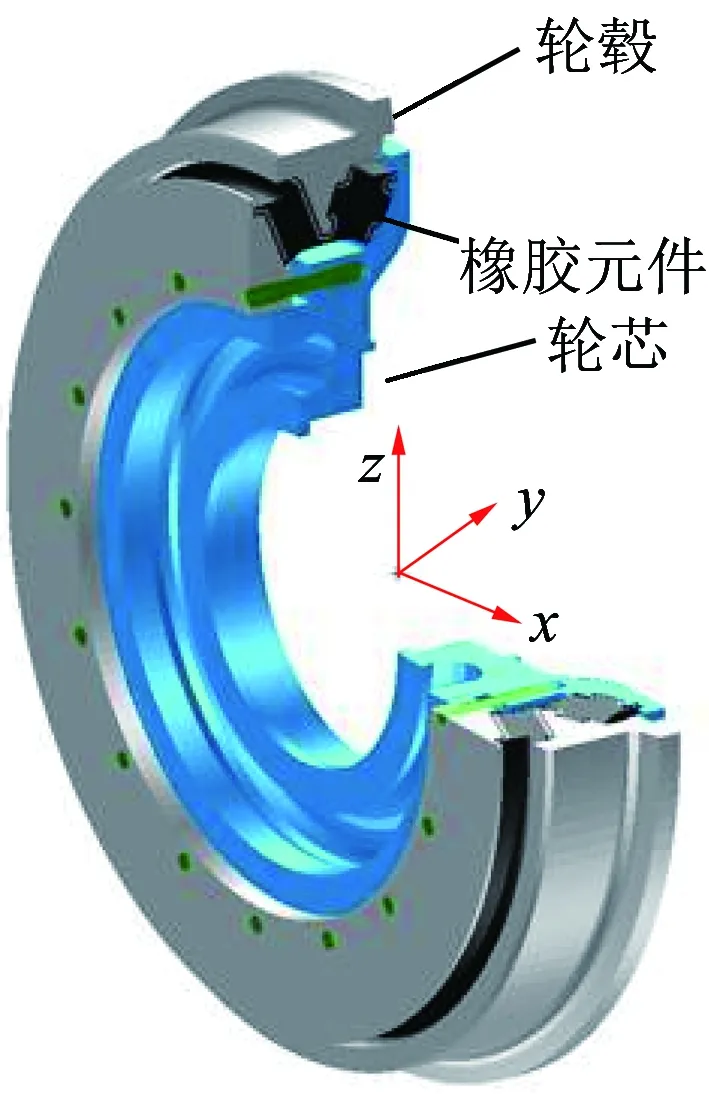
图1 压剪复合型弹性车轮结构示意图

由于压剪复合型弹性车轮的轮芯和轮毂是两个独立的部件，因此轮芯和轮毂之间具有6个自由度，分别是相对于x、y和z方向的平移自由度和旋转自由度，同时橡胶元件提供了对应的6个方向的刚度。根据弹性车轮的结构特点，x方向和z方向的水平刚度相同，统称为径向刚度，y方向的水平刚度称为轴向刚度。绕x方向和z方向的旋转刚度相同，统称为偏转刚度，绕y方向的旋转刚度称为扭转刚度。橡胶元件的各向刚度一般通过实验测量或有限元分析方法获得。

弹性车轮的轮对动力学模型包括一根车轴、两个轮芯、两个轮毂和两个轴箱，如图2所示。车轴和轮芯由于是过盈配合，因此无相对运动，而车轴与轴箱通过轴承连接， 因此轴箱相对车轴仅有绕y方向的转动自由度。与传统刚性车轮相比，弹性车轮的左侧和右侧轮毂均与轮芯相互独立，因此在左右轮毂和轮芯之间分别设置力元，体现橡胶元件的刚度特性。

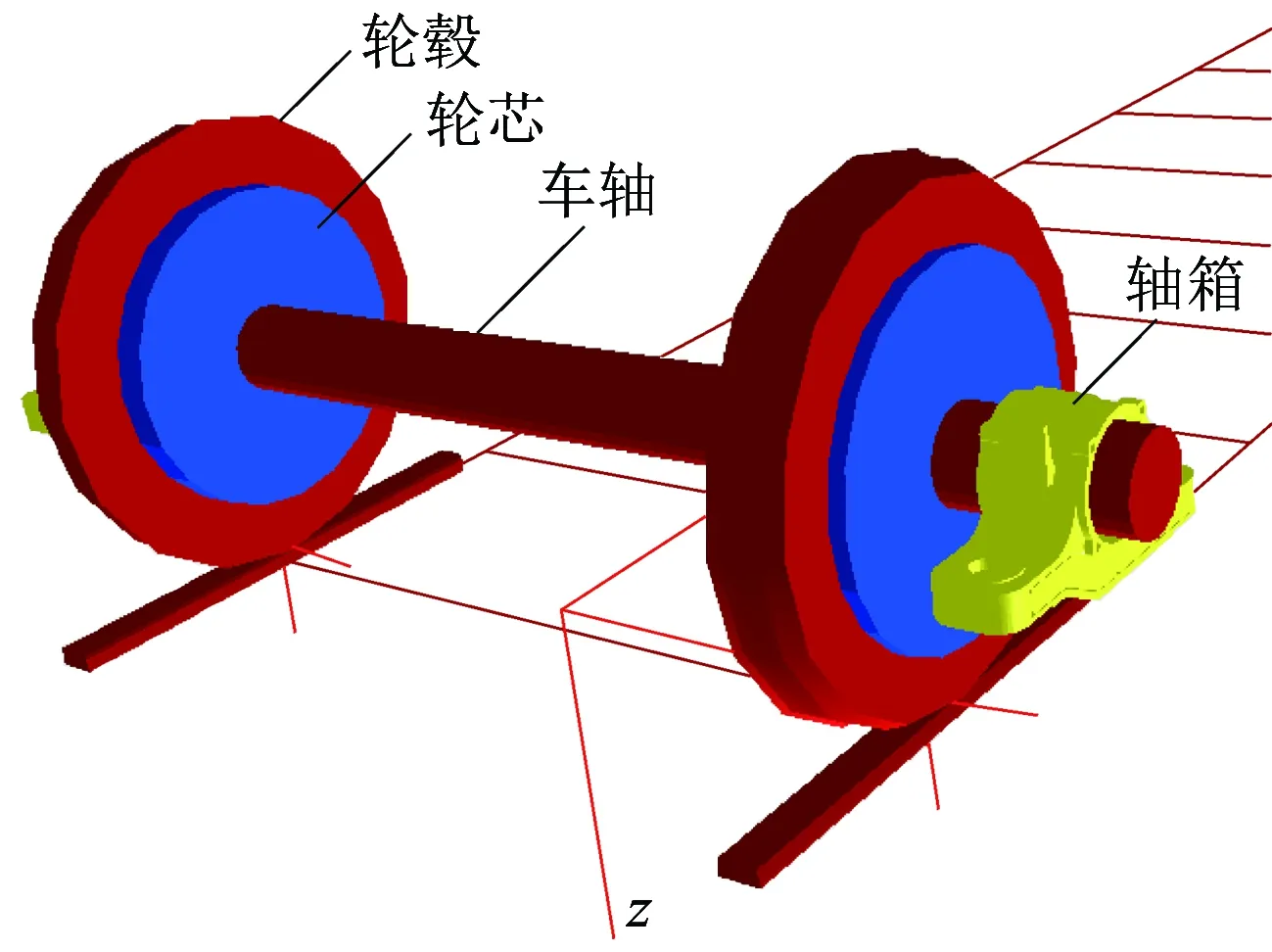
图2 弹性车轮动力学模型

2 车轮磨耗仿真模型

根据车轮型面磨耗预测的原理，其仿真流程如图3所示。具体为：

(1)通过车辆动力学仿真计算得到轮对横移量、轮对冲角、蠕滑率和轮轨垂向力等参数，同时获得车轮上的接触点分布位置。

(2)根据车轮材料磨耗原理，计算每一次轮轨接触过程中车轮材料的磨耗量并进行累积，最终得到车轮踏面上的磨耗深度分布并记录与之对应的运行里程。

(3)当累积磨耗深度的最大值达到0.1 mm时，对车轮踏面进行计算和平滑处理，得到磨耗后的车轮踏面形状。

(4)将磨耗后的车轮踏面代替磨耗前的车轮踏面，并再次进行动力学仿真。

通过以上4个步骤的循环仿真，最终求得车轮型面变化与里程的关系。

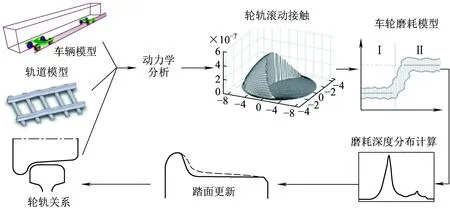
图3 车轮踏面磨耗仿真流程

2.1 半赫兹接触模型

车轮的磨耗是由轮轨滚动接触产生的，因此轮轨滚动接触模型在车轮磨耗的计算中十分重要。轮轨接触中常用的赫兹接触理论基于弹性半空间假设，其计算精度只有在两个接触体的曲率是常数时才能满足要求，而轮轨型面的曲率在发生磨耗后通常不再是常数。采用有限元方法在计算轮轨接触时，不受限于弹性半空间的假设，但缺点在于计算效率低，不适用于车轮磨耗的计算。

为了兼顾轮轨滚动接触计算的精度和效率，在磨耗仿真中采用轮轨半赫兹接触理论[6]。该理论将轮轨接触区域沿轮轨滚动方向划分为K个宽度为Δy的条带，条带中心的横坐标为yi(i=1,2,…,K)。

根据式(1)对每个条带上的相对曲率Ai和Bi进行修正。

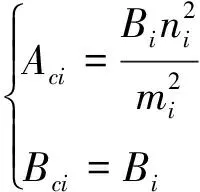
(1)

式中：mi、ni为赫兹接触条件下的轮轨接触参数；Ai和Bi为赫兹接触条件下的相对曲率。

根据半赫兹接触原理，轮轨间的法向间隙z(x,yi) 为

z(x,yi)=zw(yi)-zr(yi)+Acix2

(2)

式中：zw(yi)和zr(yi)分别为车轮和钢轨型面在相应条带处的法向位置。

轮轨接触的边界条件为

hi=h0-z(x=0,yi)≥0

(3)

式中：hi为每个条带上的轮轨接触渗入量；h0为z(x=0,yi)的值最小时的渗入量，此处的条带被称为母带。

接触条带上的纵向半轴长ai为

(4)

其中，母带位置处的纵向半轴长为a0。

接触条带上的法向力Ni为

(5)

接触斑内每个条带上的纵向接触应力σx,i和横向接触应力σy,i如式(6)、式(7)所示，与每个条带位置处的轮轨纵向蠕滑率ξx,i、横向蠕滑率ξy,i和自旋蠕滑率ξz,i有关，同时也与蠕滑系数C11,i、C22,i和C23,i有关。每个条带上的法向接触应力σz,i如式(8)所示。

(6)

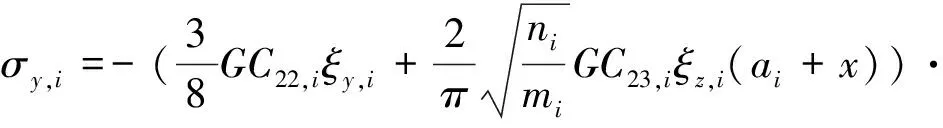
(7)

(8)

式中：G为轮轨材料的弹性剪切模量。

2.2 车轮磨耗模型

国外学者根据轮轨磨耗试验和现场实测数据建立了多种车轮磨耗模型，如Pearce基于车轮材料损失面积和能量耗散的关系建立的车轮磨耗模型[7]、Zobory基于磨耗能量流密度建立的车轮磨耗模型[8]、Jendel基于Archard 滚动接触磨耗理论建立的车轮磨耗模型[9]以及Braghin建立的车轮踏面磨耗深度快速计算模型[10]。文献[11]采用以上几种磨耗模型分别对中国铁路货车车轮的磨耗行为进行了仿真，包括磨耗后的车轮踏面形状和圆周磨耗率，并与实测结果进行对比，结果表明Zobory磨耗模型更适用于中国铁路的车轮磨耗仿真。因此，本文中对弹性车轮进行磨耗预测时将采用Zobory磨耗模型。

在Zobory磨耗模型中，接触斑划分为nx×ny个单元格，并根据轮轨蠕滑状态将接触斑分为黏着区Aa和滑动区As，如图4所示。根据轮轨蠕滑理论，只有滑动区内有磨耗发生，黏着区内的磨耗为0。接触斑内的磨耗能量流密度为[7]

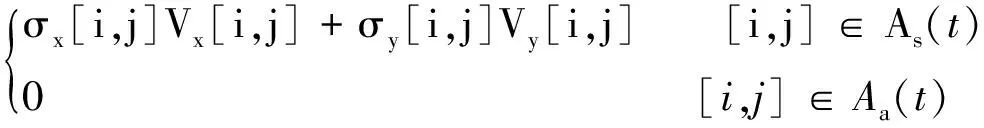
(9)

式中：Ed为磨耗能量流密度；Vx和Vy分别为轮轨纵向和横向滑动速度；i=1, 2,…,nx；j=1, 2,…,ny。

md[i,j]=k[i,j]·Ed[i,j]

(10)

式中：md为磨耗质量流密度，k为与能量流密度有关的磨耗系数。修正后的磨耗系数与能量流密度的关系如图5所示[11]。

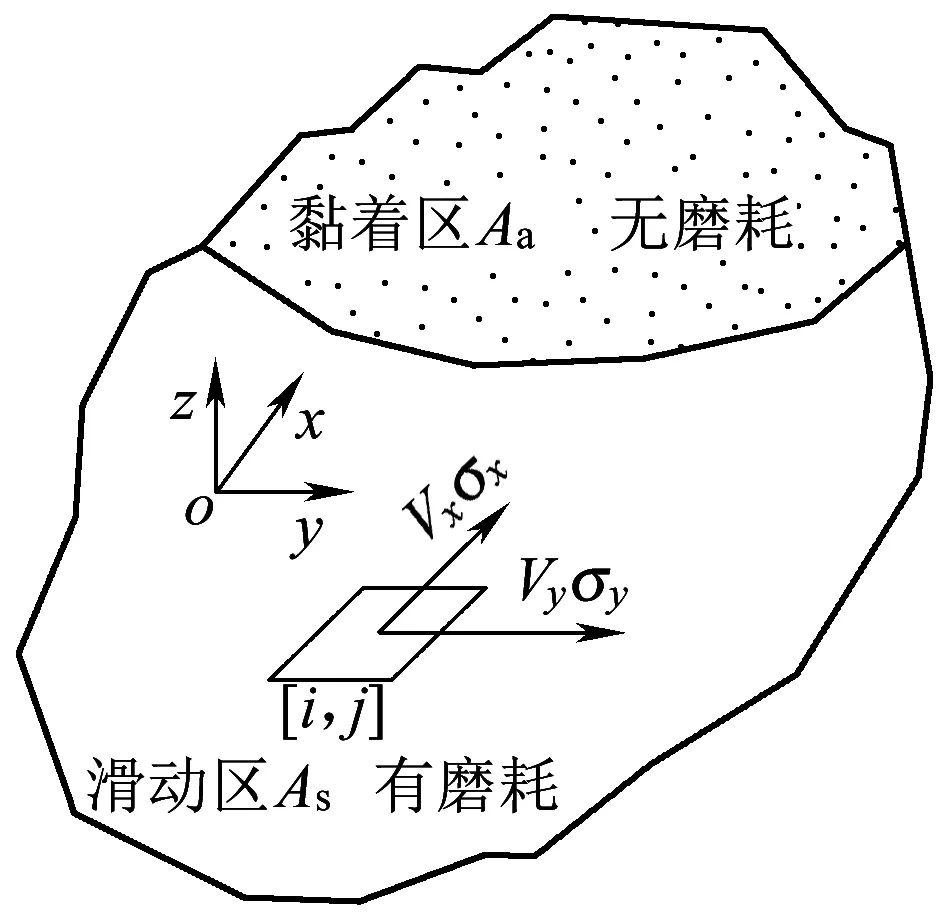
图4 接触斑内的黏着区和滑动区

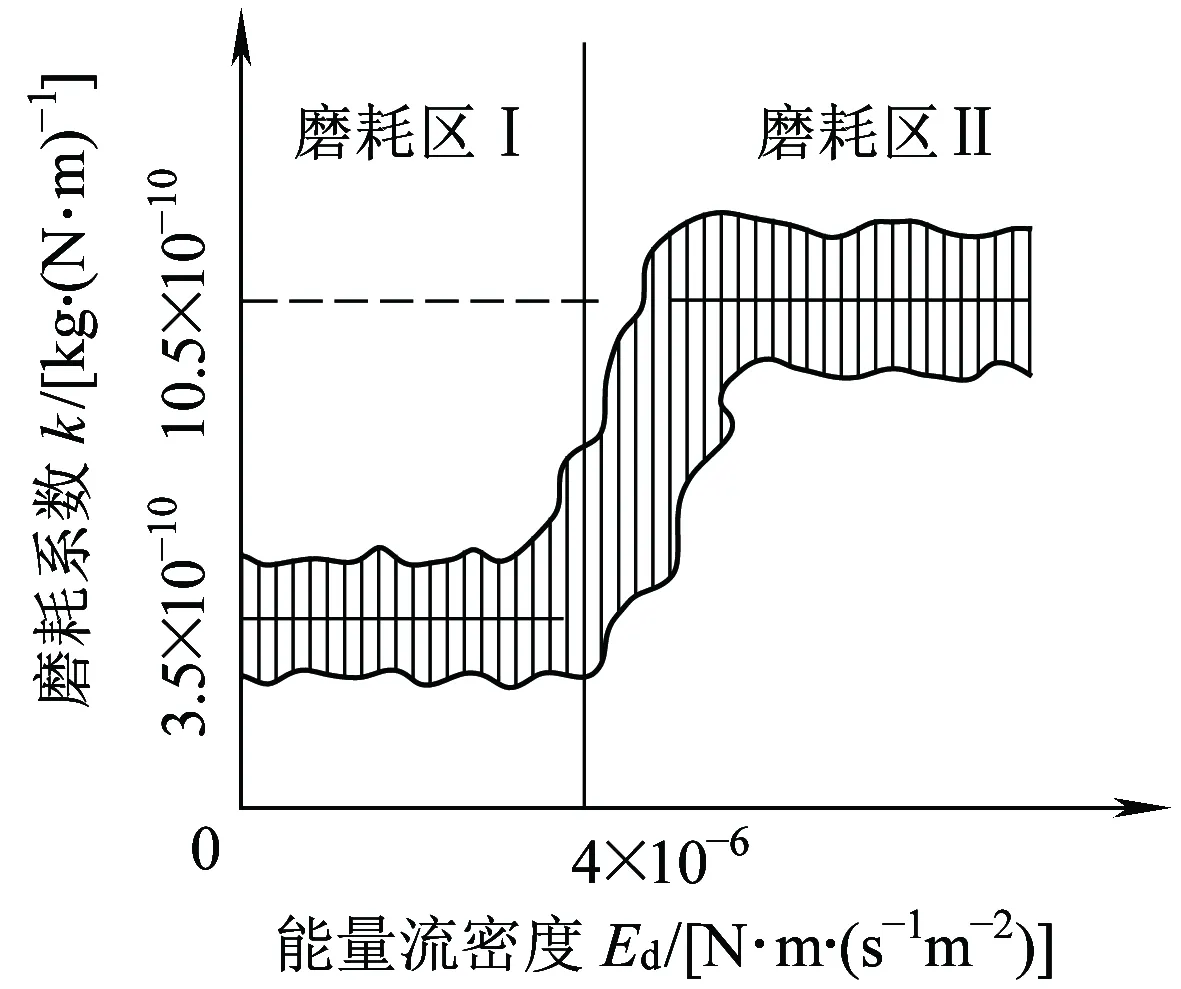
图5 修正后的磨耗系数

3 弹性车轮磨耗数值模拟

3.1 弹性车轮磨耗仿真

以国内某地铁为例，建立采用弹性车轮的地铁车辆动力学模型，如图6所示。该地铁线路全长26.5 km，曲线区段长度为8.5 km，最小曲线半径为350 m，最大曲线半径为3 000 m。根据实际线路条件(超高、缓和曲线长度、圆曲线长度等)建立线路模型，模拟地铁车辆在该线路上运行时的轮轨动力学性能。

图6 车辆动力学模型

根据图3的车轮磨耗仿真流程，采用弹性车轮的地铁车辆的车轮踏面形状随运营里程的变化如图7所示，磨耗在踏面上的分布如图8所示。可见车轮轮缘和踏面上均有磨耗发生，以踏面磨耗为主；磨耗分布范围在-55～56 mm之间，运营里程越大，磨耗分布范围越宽。

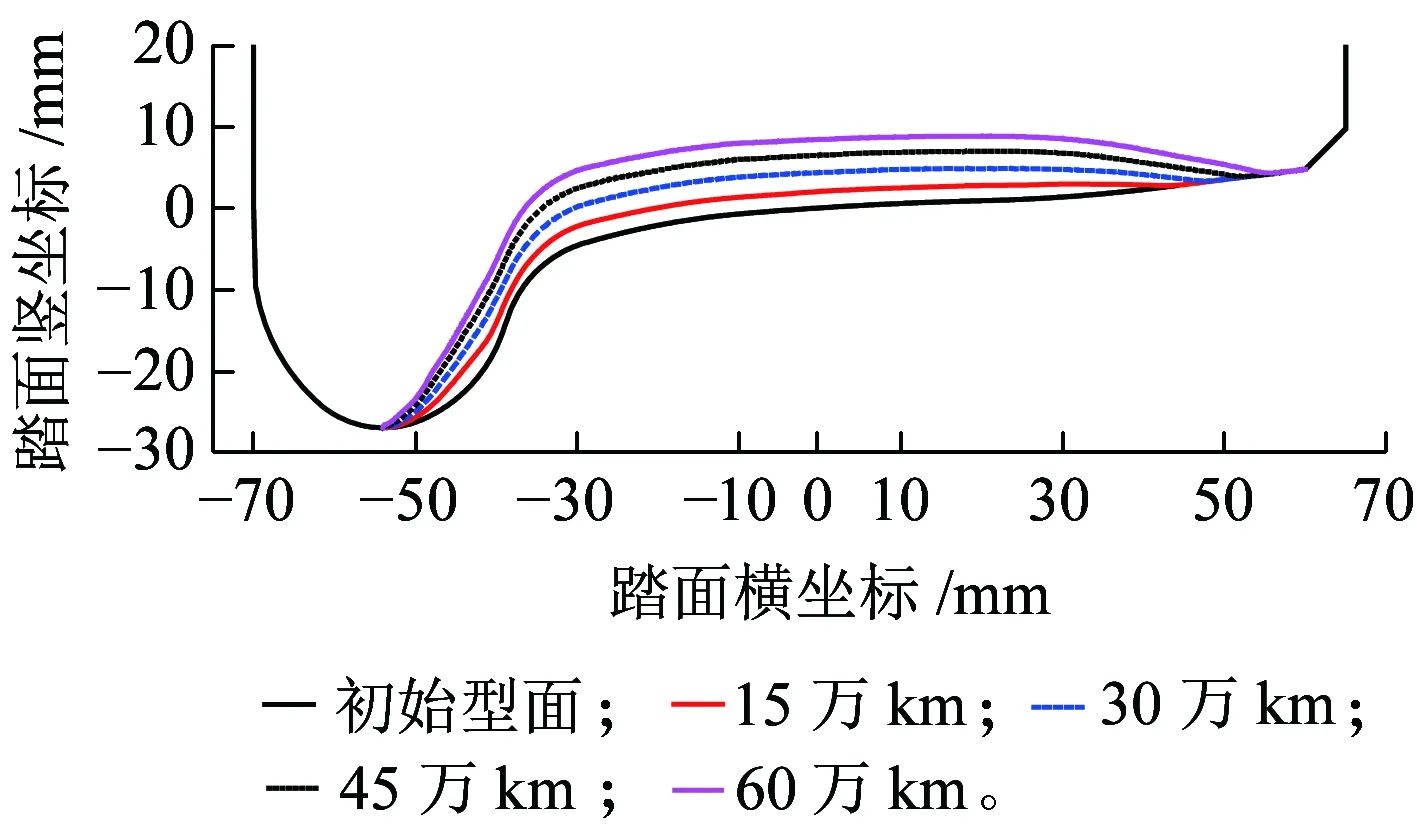
图7 磨耗后的车轮踏面形状

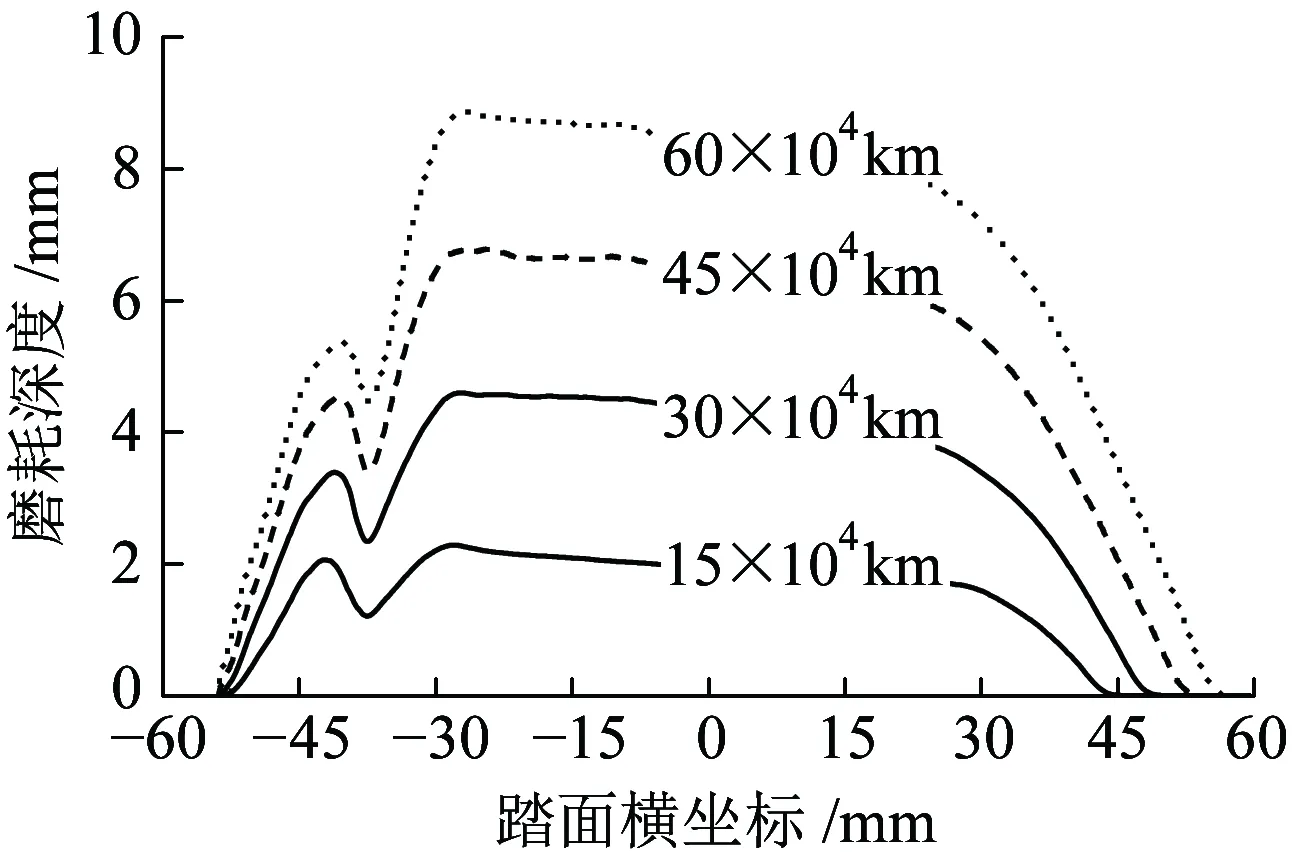
图8 车轮踏面上的磨耗深度分布

车轮的圆周磨耗深度和轮缘厚度随运行里程的变化如图9所示。结果表明，随着运营里程的增大，圆周磨耗深度线性增加，而轮缘厚度则逐渐减小，说明车轮轮缘发生了一定的磨耗。根据地铁车辆维修规则，当车轮圆周磨耗深度达到8 mm或者轮缘厚度小于26 mm时，需要对车轮进行镟修。对于弹性车轮，即使运营里程达到60万km后，车轮的轮缘厚度也不小于26 mm，而当运营里程达到57.5万km后，圆周磨耗深度达到8 mm，需要进行镟修，也即车轮的镟修寿命为57.5万km。

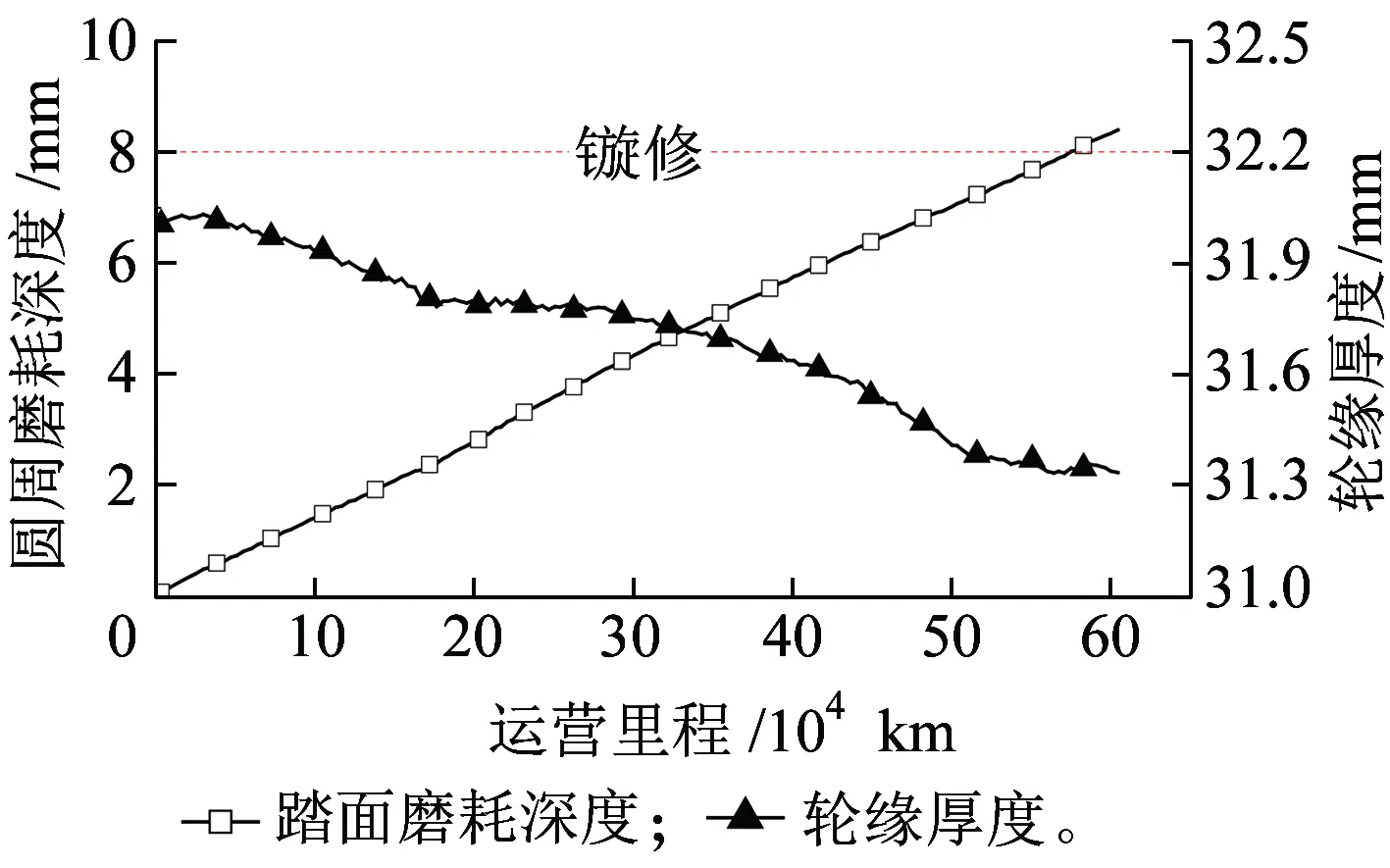
图9 车轮参数与运营里程的关系

3.2 弹性车轮和刚性车轮的磨耗对比分析

将地铁车辆动力学模型中的车轮更换为刚性车轮，其余参数一致，进行车轮磨耗仿真。当车辆运营里程达到35万km后，刚性车轮磨耗后的车轮踏面如图10所示，并与相同运营里程下的弹性车轮踏面形状进行比较。磨耗深度在踏面上的分布如图11所示。

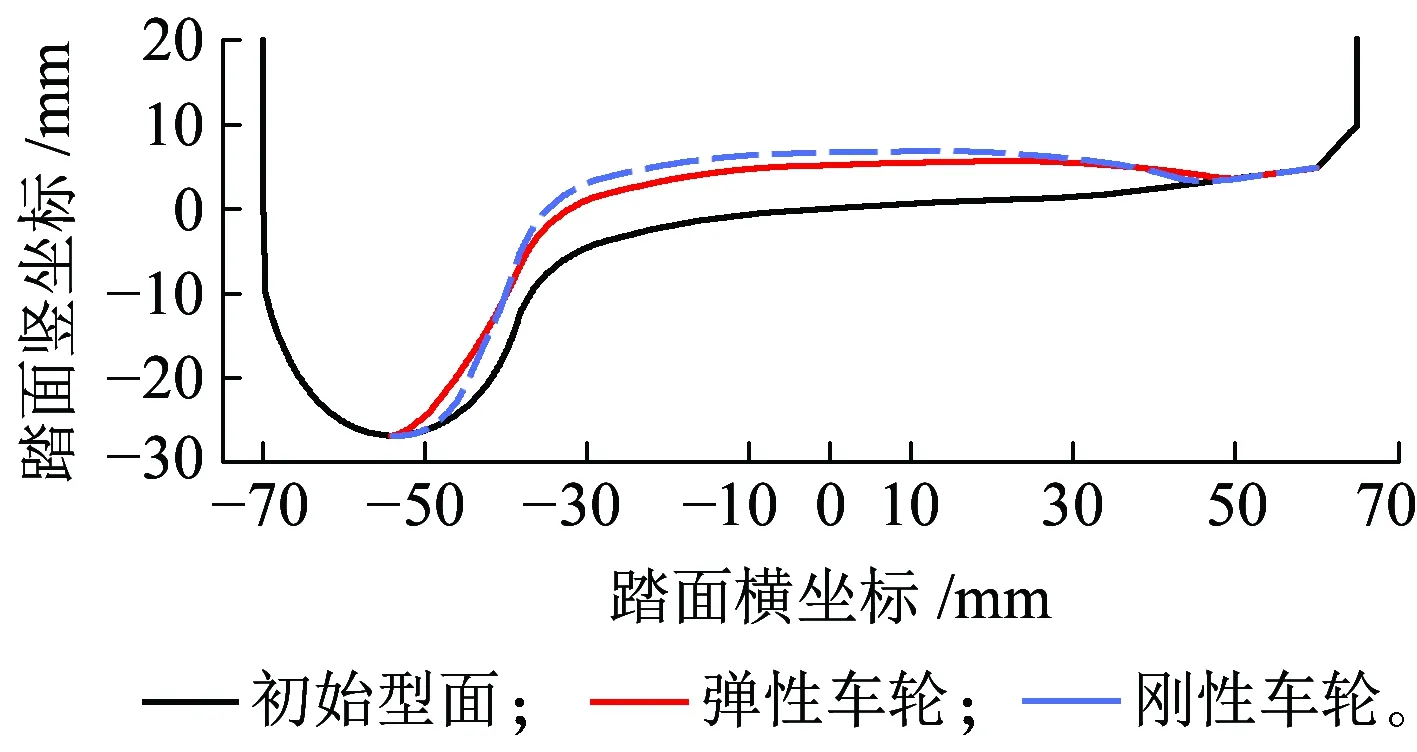
图10 磨耗后的车轮踏面形状对比(里程为35万km)

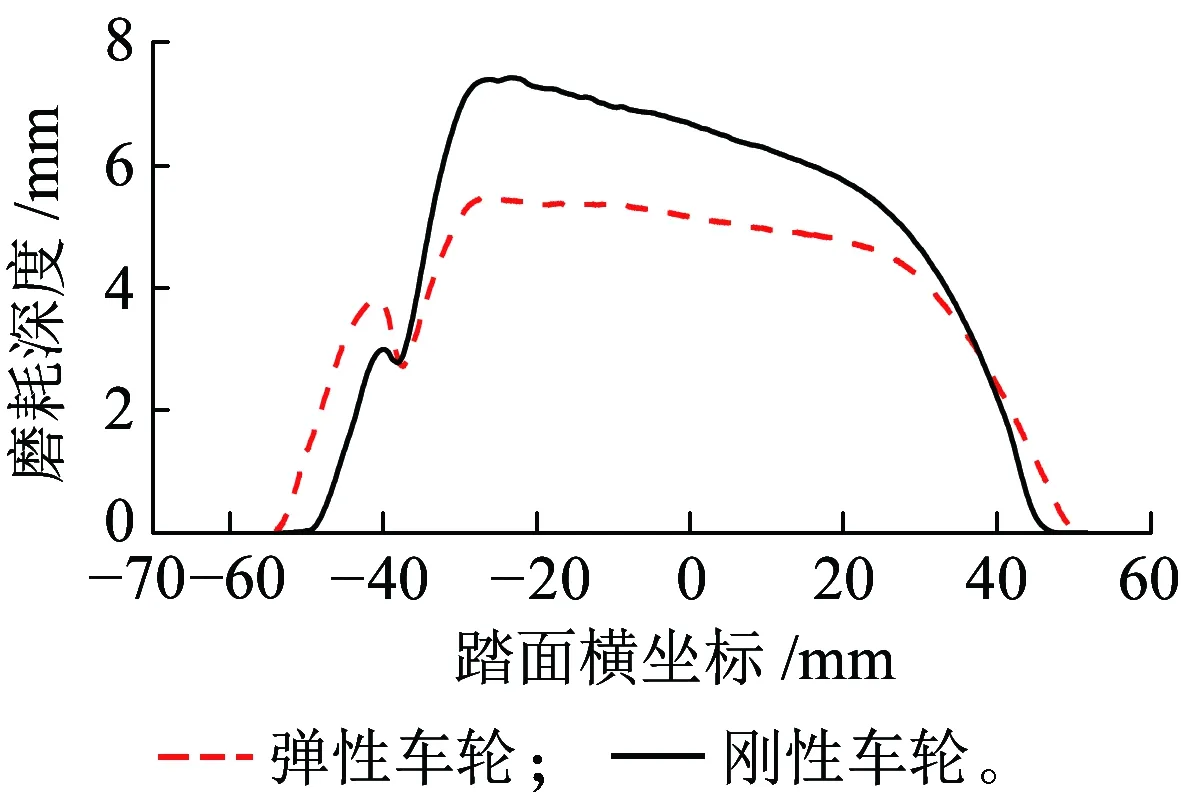
图11 磨耗分布对比(里程为35万km)

可以看出，在相同的运营里程下，弹性车轮的磨耗分布范围明显比刚性车轮宽，分布范围为-55～51 mm，而刚性车轮的分布范围为为-51～47 mm；弹性车轮在轮缘部分的磨耗略大于刚性车轮，但踏面部分的磨耗明显小于刚性车轮。

弹性车轮和刚性车轮的圆周磨耗深度和轮缘厚度随运行里程的变化如图12所示。从图12可以看出：刚性车轮的圆周磨耗深度随着运营里程的增加线性增大，而轮缘厚度随着运营里程的增加先减小后增大；刚性车轮运营里程达到45万km时，圆周磨耗深度达到8 mm，需要镟轮。因此，弹性车轮的镟修寿命较刚性车轮增加27.8 %。

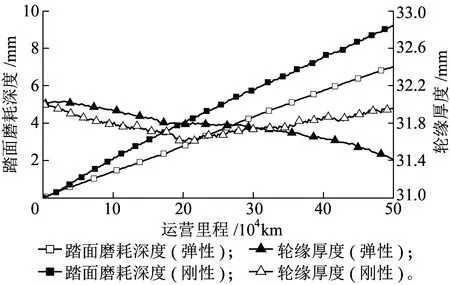
图12 弹性车轮和刚性车轮磨耗参数对比

4 橡胶元件刚度对弹性车轮磨耗的影响

轮芯和轮毂之间的橡胶元件是弹性车轮与刚性车轮的主要区别所在。国内应用于有轨电车的某型号弹性车轮橡胶元件的径向刚度为240 MN/m，轴向刚度为20 MN/m，偏转刚度和扭转刚度分别为2.5 MN·m/rad和400 MN·m/rad。为了分析橡胶元件刚度对弹性车轮磨耗的影响，将径向刚度范围设置为120～480 MN/m，轴向刚度范围为5～80 MN/m，偏转刚度范围为1.0～10 MN·m/rad，扭转刚度范围为100～1 200 MN·m/rad。在仿真计算中，当其中一个刚度变化时，其余刚度均取某型号弹性车轮的原始值。

4.1 径向刚度

当弹性车轮的径向刚度分别为120 MN/m、240 MN/m和480 MN/m，且运营里程达到40万km时，磨耗后的车轮踏面如图13所示。可以看出，橡胶元件的径向刚度对弹性车轮磨耗的影响较小，当径向刚度由120 MN/m分别增大到240 MN/m 和480 MN/m时，镟修寿命分别增加1.95%和6.9%。

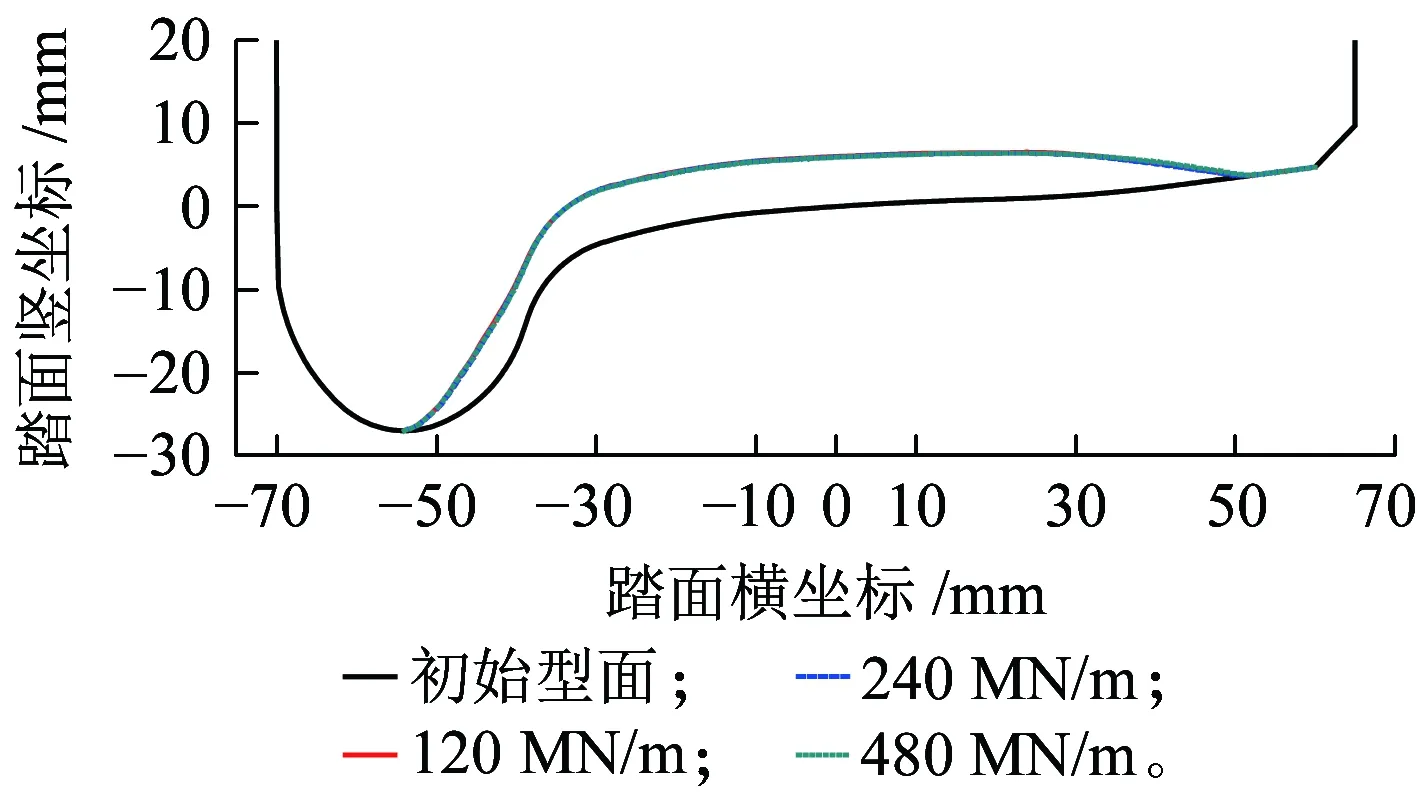
图13 橡胶元件径向刚度对车轮磨耗的影响

在磨耗计算中，弹性车轮的径向刚度主要影响车轮的垂向载荷，而径向刚度远大于转向架的一系和二系垂向刚度，因此径向刚度对弹性车轮的磨耗影响较小。

4.2 轴向刚度

当弹性车轮的轴向刚度分别为5 MN/m、20 MN/m和80 MN/m，且运营里程达到40万km时，磨耗后的车轮踏面如图14所示。可以看出，橡胶元件轴向刚度对车轮的磨耗有较明显的影响，随着轴向刚度的减小，车轮的磨耗范围和轮缘磨耗随之变大，而圆周磨耗略有减小；当轴向刚度由5 MN/m增大到20 MN/m和80 MN/m时，镟修寿命分别减少4.3%和6.8%。

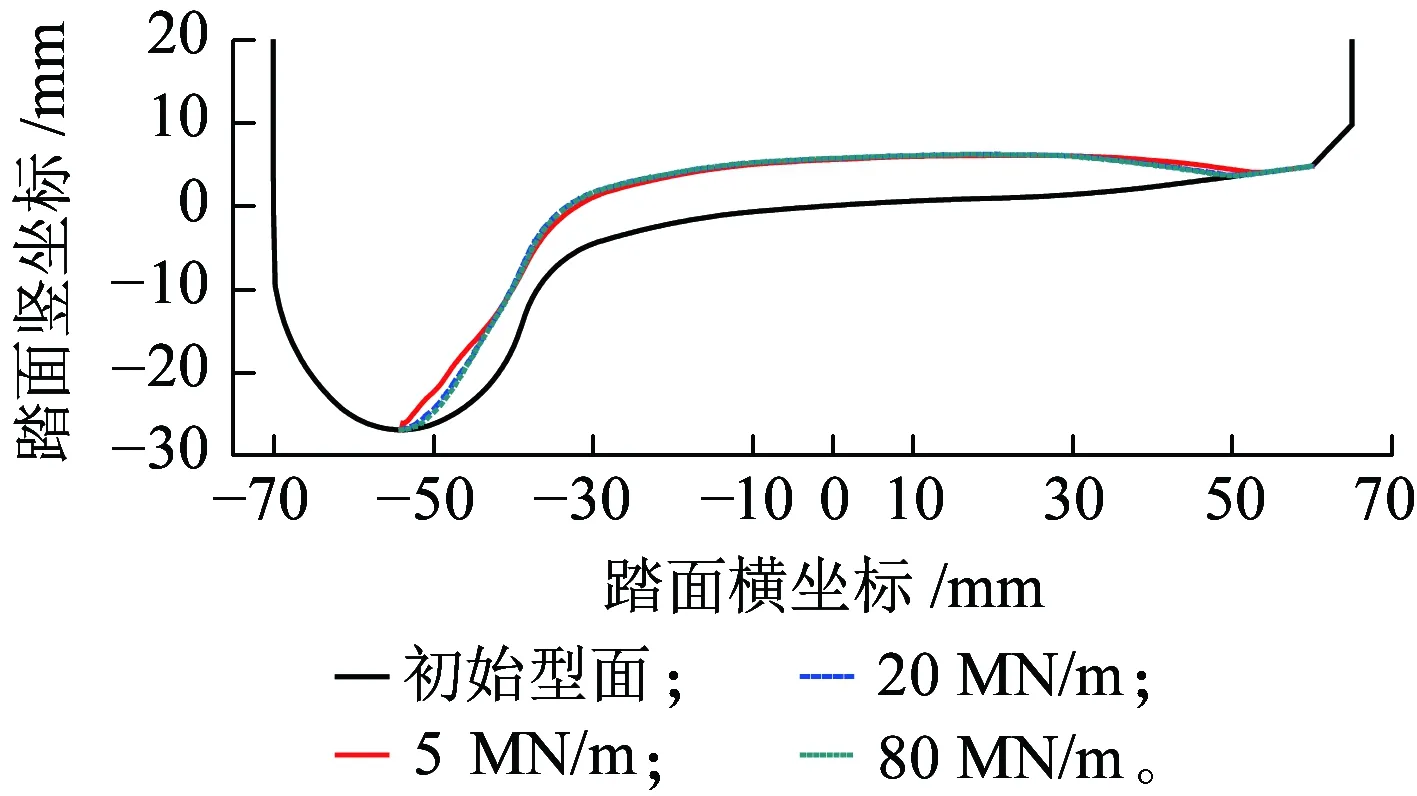
图14 橡胶元件轴向刚度对车轮磨耗的影响

轴向刚度直接影响弹性车轮的轮对横移量，在相同的轮轨横向载荷作用下，轴向刚度越小，轮对横移量越大，不仅增加车轮踏面磨耗，同时会导致严重的车轮轮缘磨耗和钢轨侧磨。因此，在弹性车轮橡胶元件设计中，应选取较大的轴向刚度。

4.3 偏转刚度

当弹性车轮的偏转刚度分别为1.0 MN·m/rad、2.5 MN·m/rad和10 MN·m/rad，且运营里程达到40万km时，磨耗后的车轮踏面如图15所示。可以看出，橡胶元件偏转刚度主要影响车轮的轮缘磨耗，对圆周磨耗的影响较小。偏转刚度越小，车轮的磨耗范围越宽，轮缘的磨耗越大，同时圆周磨耗略有减小。当偏转刚度由1.0 MN·m/rad增大到2.5 MN·m/rad和10 MN·m/rad时，镟修寿命分别减小1.7%和3.3%。

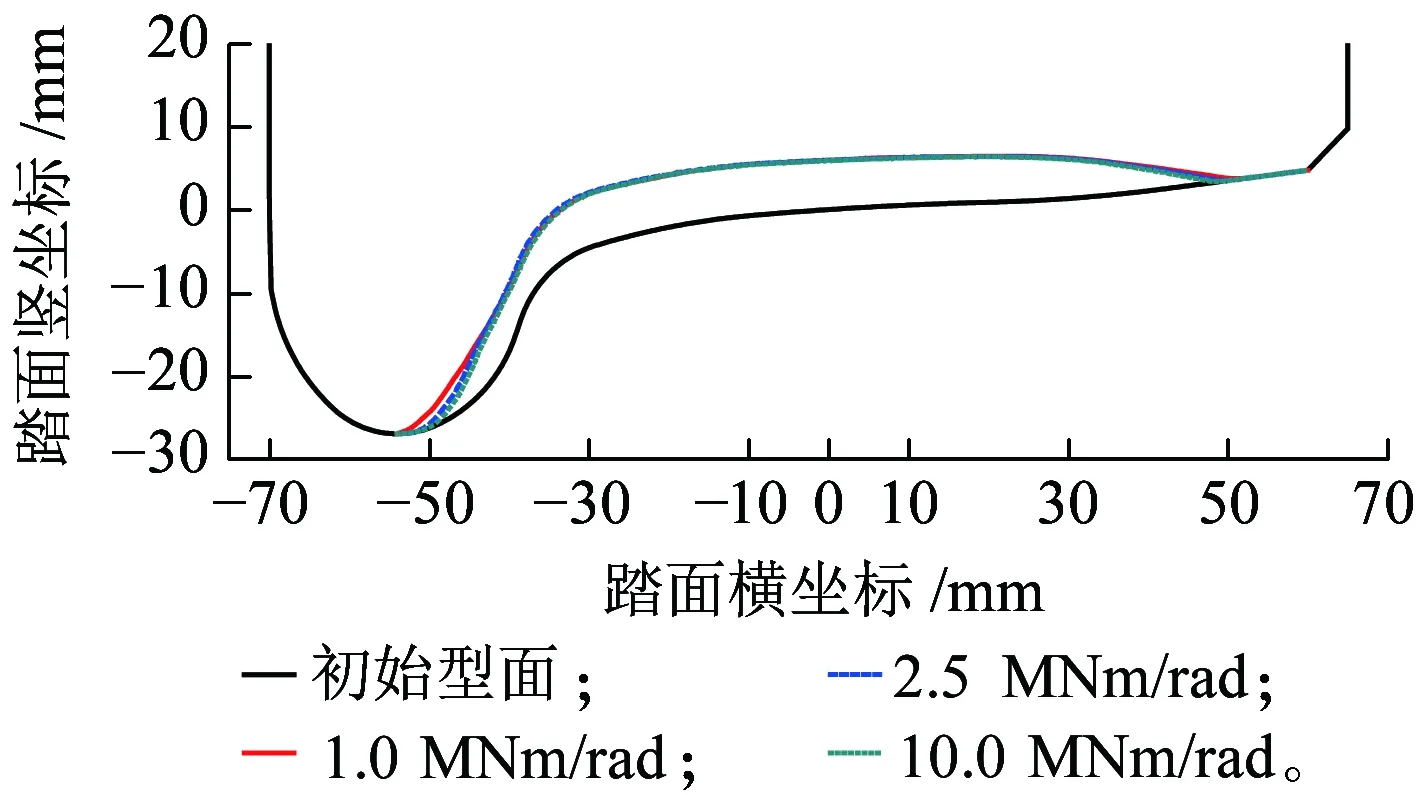
图15 橡胶元件偏转刚度对车轮磨耗的影响

弹性车轮的偏转刚度主要影响车轮和钢轨之间的冲角，偏转刚度越小，车轮相对于钢轨的冲角越大，意味着接触位置更加靠近轮缘，从而导致轮缘磨耗和钢轨侧磨的加剧。因此，在弹性车轮中也应选取较大的偏转刚度。

4.4 扭转刚度

当弹性车轮的扭转刚度分别为100 MN·m/rad、400 MN·m/rad和1 200 MN·m/rad，且运营里程达到40万km时，磨耗后的车轮踏面如图16所示。可以看出，橡胶元件的扭转刚度对弹性车轮的轮缘磨耗和圆周磨耗的影响都较小。当扭转刚度由100 MN·m/rad增大到400 MN·m/rad和1200 MN·m/rad时，镟修寿命分别增加2.3%和2.8%。

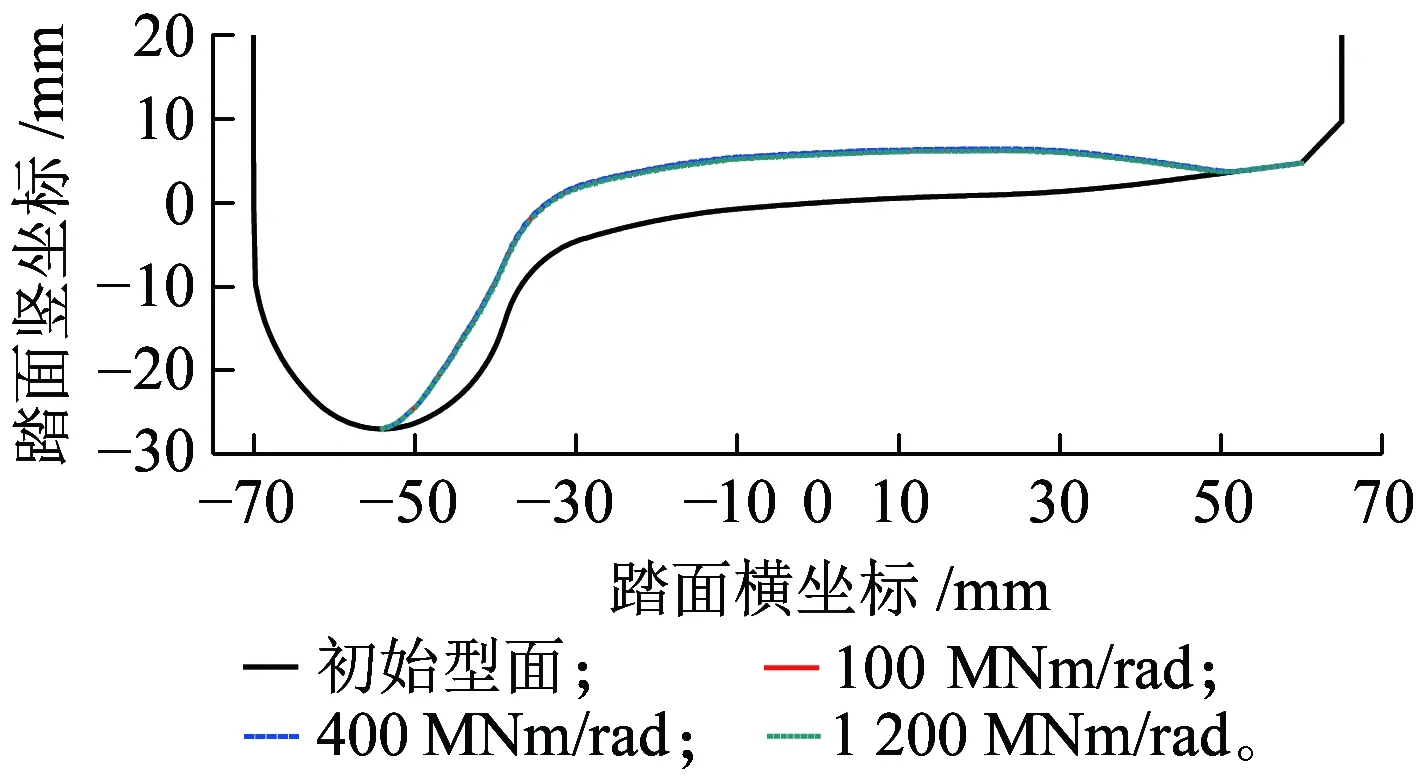
图16 橡胶元件扭转刚度对车轮磨耗的影响

弹性车轮的扭转刚度主要用于约束轮芯和轮毂在y方向的旋转自由度，为了保证车辆的运行安全性，该刚度值一般都设计得比较大，同时扭转刚度主要影响轮轨之间的蠕滑力，而扭转刚度在100～1 200 MN·m/rad范围内变化时，对轮轨蠕滑的影响较小，因此对弹性车轮的磨耗几乎没有影响。

5 结论

通过车轮磨耗数值模拟模型，对弹性车轮的磨耗行为及影响因素进行研究，并与刚性车轮进行比较，得到如下结论：

(1)与刚性车轮相比，弹性车轮磨耗范围较宽，同时轮缘磨耗大于刚性车轮，但圆周磨耗明显小于刚性车轮。在相同的运营条件下，弹性车轮的镟修寿命较刚性车轮增大27.8%。因此，采用弹性车轮，不仅能降噪减振，也能减轻车轮磨耗，延长车轮使用寿命。

(2)弹性车轮中橡胶元件的径向刚度和扭转刚度仅对圆周磨耗有较小的影响，而轴向刚度和偏转刚度主要影响轮缘磨耗，车轮的镟修寿命因轴向刚度和偏转刚度的增大略有减小。在对弹性车轮橡胶元件刚度进行设计时，应对轮缘磨耗和镟修寿命进行综合考虑。

参考文献：

[1]SUAREZ B, CHOVER J A, RODRIGUEZ P, et al. Effectiveness of Resilient Wheels in Reducing Noise and Vibrations [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2011, 225(6): 545-565.

[2]KOUROUSSIS G, VERLINDEN O, CONTI C. Efficiency of Resilient Wheels on the Alleviation of Railway Ground Vibrations [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2012, 226(4): 381-396

[3]WAKUI H. Subjects for Wheel/rail System Related to Wheel/Track Impact[J]. RTRI Report, 2003,17(19):1-8.

[4]刘玉霞，韩健，周信，等. 弹性车轮减振降噪特性分析[J].铁道学报，2015,37(6)：48-53.

LIU Yuxia, HAN Jian, ZHOU Xin, et al. Analysis of Vibration and Noise Reduction Characteristics of Resilient Wheel [J]. Journal of the China railway society, 2015, 37(6):48-53.

[5]邢璐璐. 弹性车轮车辆动力学研究[D]. 成都：西南交通大学，2012.

[6]AYASSE J B，CHOLLET H. Determination of the Wheel Rail Contact Patch in Semi-hertzian Conditions[J]. Vehicle System Dynamics，2005，43(3)：161-172.

[7]PEARCE T G, SHERRATT N D. Prediction of Wheel Profile Wear [J]. Wear, 1991, 144(1): 343-351.

[8]ZOBORY I. Prediction of Wheel/rail Profile Wear[J]. Vehicle System Dynamics，1997，28(2)：221-259.

[9]JENDEL T. Prediction of Wheel Profile Wear-comparisons with Filed Measurements[J]. Wear，2002，253(1)：89-99.

[10]BRAGHIN F, LEWIS R, Dwyer R S. A Mathematical Model to Predict Railway Wheel Profile Evolution Due to Wear[J]. Wear, 2006, 261(11): 1 253-1 264.

[11]丁军君. 基于蠕滑机理的重载货车车轮磨耗研究[D]. 成都：西南交通大学，2012.