FI代数的模糊软滤子

刘春辉

(赤峰学院 数学与统计学院, 内蒙古 赤峰 024001)



FI代数的模糊软滤子

刘春辉

(赤峰学院 数学与统计学院, 内蒙古 赤峰 024001)

摘要：将模糊软集概念及其相关运算应用于FI代数的滤子理论研究,引入FI代数的模糊软滤子概念, 给出它的若干代数性质,定义FI代数间的模糊软FI-同态(同构)概念,并证明FI代数的一个模糊软滤子在模糊软FI-同构(同态)下的像(原像)仍为模糊软滤子.

关键词：FI代数; 模糊软集; 模糊软滤子; 模糊软FI-同态(同构)

1预备知识

非经典数理逻辑理论[1]的一个重要研究分支是对逻辑代数系统的研究.Fuzzy蕴涵代数(简称:FI代数)是由我国学者吴望名于1990年提出的,它揭示了蕴涵算子的共同本质,是蕴涵连接词的代数化[2].大部分著名的逻辑代数系统(如BL代数、MV代数、MTL代数、R0代数、格蕴涵代数等)都可以看成是FI代数的自然扩张,因此对FI代数性质的研究具有广泛而基本的重要意义.迄今为止,这方面已获得很多有价值的研究成果[3-5].D. Molodtsov在文献[6]中提出了软集的概念,试图从参数化的角度为不确定性问题的研究提供一个统一的数学框架.作为一种新的处理不确定性问题的数学工具,软集理论与模糊集理论和粗糙集理论等具有很强的互补性,理论和应用研究受到了学术界的广泛关注[7-12].将模糊集[13]与软集相结合,P. K. Maji等在文献[14]中提出了模糊软集的概念并给出其若干运算性质.文献[15-16]将模糊软集的概念与群和环等抽象代数结构相结合,提出了模糊软群和模糊软环等概念并讨论了它们的性质.文献[17-18]又将模糊软集概念与BCK/BCI代数和d-代数相结合提出并研究了模糊软BCK/BCI代数、模糊软d-代数及其模糊软理想的性质特征.这些研究工作一方面很好地促进了模糊软集与代数结构的相互融合,另一方面也丰富和完善了模糊软集理论的研究内容.

在上述研究工作的基础上,本文将模糊软集的概念与FI代数的模糊滤子概念相结合,提出了FI代数的模糊软滤子概念并讨论其性质,获得了一些有意义的结果.

定义 1.1[2]称(2,0)型代数(X,→,0)为Fuzzy蕴涵代数,简称X为FI代数,若∀x,y,z∈X满足:

(ⅰ)x→(y→z)=y→(x→z);

(ⅱ) (x→y)→((y→z)→(x→z))=1;

(ⅲ)x→x=1;

(ⅴ) 0→x=1,

其中1=0→0.

定义 1.2[2]设X、Y是2个FI代数,f:X→Y是映射.若∀x,y∈X,有f(x→y)=f(x)→f(y),则称f为X到Y的FI-同态.若FI-同态f是单射(满射),则称f为单FI-同态(满FI-同态).若FI-同态f是双射,则称f为FI-同构.

注 1.1设X、Y是2个FI代数,f为X到Y的FI-同态,则f(1)=1.

定义 1.3[13]集合X上的一个模糊集指的是映射μ:X→[0,1].

定义 1.4[3]称FI代数X上的模糊集μ为X的模糊滤子,如果∀x,y∈X有μ(1)≥μ(x)且μ(y)≥min{μ(x),μ(x→y)}.

注 1.2易证,FI代数X的任一模糊滤子族的模糊交仍为X的模糊滤子.

定义 1.5[6]设U是一个集合,P(U)是U的幂集,E是一个参数集.A⊆E且F:A→P(U)是一个映射,称二元组(F,A)为U上的一个软集.

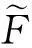
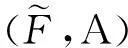
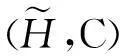
其中C=A∪B,且∀e∈C,

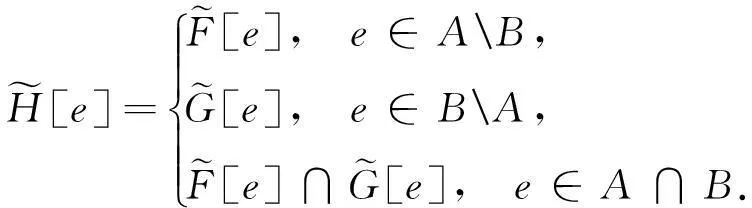
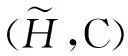
其中C=A∩B≠∅,且

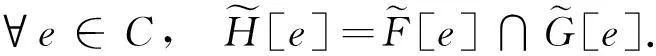
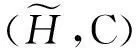
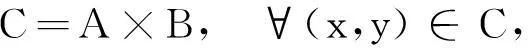
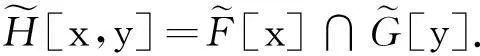
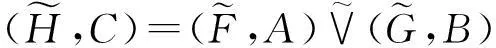
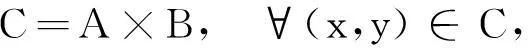
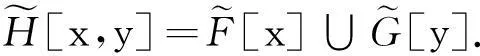
2模糊软滤子的定义及其代数性质

例 2.1设X={c1,c2,c3,c4}={“白色”,“红色”,“绿色”,“蓝色”}表示4 种不同的颜色,在X上定义二元运算→如表1所示.

表 1　X上定义二元运算

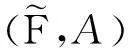
证明由定义直接可得.

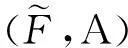
不是X的模糊滤子,这是因为

定理2.2～2.4推广到X的任意多个模糊软滤子的情形也成立,证明方法类似.

根据文献[13],设μ1∈F(X)且μ2∈F(Y),则

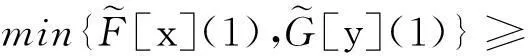
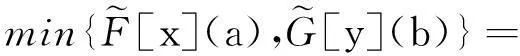
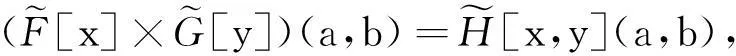
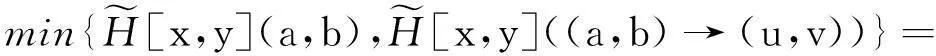
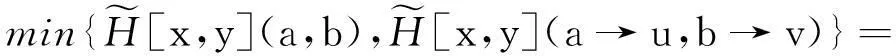
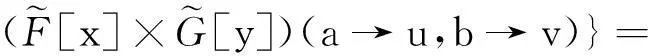
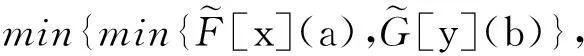
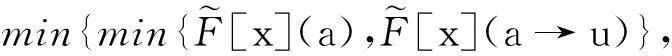
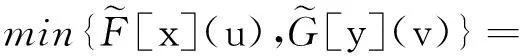
3模糊软滤子的模糊软FI-同态像与原像

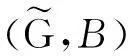
任取y∈Y,由f为FI-同构知存在唯一的x∈X使得x∈f-1(y).注意到f(1)=1,对任意的∀e′∈g(A)得

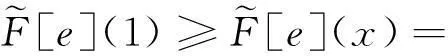
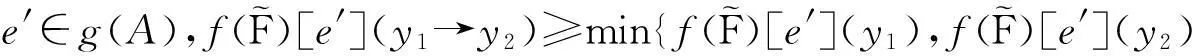
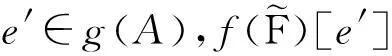
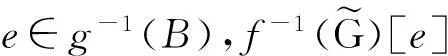
参考文献

[1] 王国俊. 非经典数理逻辑与近似推理[M]. 北京:科学出版社,2003.

[2] 吴望名. Fuzzy蕴涵代数[J]. 模糊系统与数学,1990,4(1):56-64.

[3] 刘春辉,徐罗山. FI代数的多种Fuzzy滤子[J]. 模糊系统与数学,2010,24(2):21-27.

[4] 裴道武,王三民,杨瑞. 模糊蕴涵格理论[J]. 高校应用数学学报,2011,26(3):343-354.

[5] 刘春辉. Fuzzy蕴涵代数的滤子理论[J]. 山东大学学报(理学版),2013,48(9):73-77.

[6] MOLEDTSOV D. Soft set theory-first results[J]. Comput Math Appl,1999,37(4/5):19-31.

[7] MAJI P K, BISWAS R, ROY A R. Soft set theory[J]. Comput Math Appl,2003,45:555-562.

[8] AKTAS H, CAGMAN N. Soft sets and soft groups[J]. Information Sciences,2007,177:2726-2735.

[9] FENG F, JUN Y B, ZHAO X Z. Soft semirings[J]. Comput Math Appl,2008,56:2621-2628.

[10] JUN Y B. Soft BCK/BCI-algebras[J]. Comput Math Appl,2008,56:1408-1413.

[11] 刘春辉. 滤子化软FI代数[J]. 山东大学学报(理学版),2012,47(11):94-98.

[12] 刘春辉. 软FI代数及其软MP滤子[J]. 四川师范大学学报(自然科学版),2013,36(6):851-855.

[13] ZADEH L A. Fuzzy sets[J]. Information Control,1965,8:338-353.

[14] MAJI P K, BISWAS R, ROY A R. Fuzzy soft sets[J]. J Fuzzy Math,2001,9(3):589-602.

[17] JUN Y B, LEE K J, PARK C H. Fuzzy soft sets theory applied to BCK/BCI-algebras[J]. Comput Math Appl,2009,57:367-378.

[18] JUN Y B, LEE K J, PARK C H. Fuzzy soft sets theory applied to ideals in d-algebras[J]. Comput Math Appl,2010,59:3180-3192.

2010 MSC：03G25; 03E72; 06B05; 06B10

(编辑郑月蓉)

Fuzzy Soft Filters of FI-Algebras

LIU Chunhui

(DepartmentofMathematicsandStatistics,ChifengUniversity,Chifeng024001,InnerMongolia)

Abstract：In this paper, we study filter’s theory of FI-algebras by applying the concepts and its related operations of fuzzy soft sets. The notion of fuzzy soft filter of an FI-algebra is introduced. Some algebraic properties are discussed. The concept of fuzzy soft FI-homomorphism(isomorphism) between two FI-algebras are defined, it is proved that the fuzzy soft FI-isomorphic(homomorphic) image (and inverse image) of a fuzzy soft filter is also a fuzzy soft filter.

Key words：FI-algebra; fuzzy soft set; fuzzy soft filter; fuzzy soft FI-homomorphism

doi:10.3969/j.issn.1001-8395.2016.01.014

中图分类号：O141.1; O153.1

文献标志码：A

文章编号：1001-8395(2016)01-0083-05

作者简介：刘春辉(1982—),男,讲师,主要从事数理逻辑、Domain理论与拓扑学的研究,E-mail:chunhuiliu1982@163.com

基金项目：内蒙古自治区高等学校科学研究项目(NJSY14283)

收稿日期:2014-04-20