纳米硬/软磁复合永磁薄膜磁滞回线的微磁学理论综述
2016-05-06赵国平万秀琳
赵国平, 万秀琳
(四川师范大学 物理与电子工程学院固体物理研究所, 四川 成都 610066)
纳米硬/软磁复合永磁薄膜磁滞回线的微磁学理论综述
赵国平,万秀琳
(四川师范大学 物理与电子工程学院固体物理研究所, 四川 成都 610066)
摘要:纳米硬/软磁交换弹簧复合材料是一种新型的高性能永磁体材料,在基础研究和实际应用2个方面都得到广泛的重视.它有着丰富的磁学性质,特别是在磁能积方面潜力巨大,理论磁能积密度高达1 MJ/m3.微磁学是量子磁学和宏观磁性的桥梁,是研究材料磁滞回线和宏观磁性的重要理论,它能清晰地阐述材料的磁化反转机制,预测磁滞回线和磁性能.以薄膜结构为例,综述3种重要的计算复合磁体磁滞回线的微磁学方法:一维全解析模型;一维半解析模型;三维数值计算模型,并分别讨论3种方法的优点与不足.将不同方法得到的计算结果进行比较,重点分析硬/软磁相厚度和易磁化轴取向对复合磁体宏观磁滞回线以及矫顽力机制的影响,并与实验进行比较,讨论理论和实验产生差别的原因,提出一些提高材料磁性能特别是矫顽力和磁能积的的方法.
关键词:微磁学理论; 磁滞回线; 磁能积
纳米尺度内的交换耦合复合材料[1-2]结合了软磁相的高剩磁和硬磁相的高矫顽力,具有很高的磁能积.该材料一经提出,就受到人们的广泛关注[3-15],是目前磁学以及磁性材料领域中一个重要的研究方向[15-29].在制造磁电阻[30-40]、永磁材料[3-4,41]和巨磁致伸缩材料[42-44]等方面,交换弹簧都有着重要应用.
R. Skomski等[4]预言硬软磁复合材料最大磁能积密度(BH)max可以达到1 MJ/m3,是目前最好的单相NdFeB永磁体理论值的2倍左右,展现出诱人的前景.许多磁学工作者试图在实验中获得这样巨大的磁能积,但是实验所得到的结果仅有理论值的20%~40%[5,45-48],迄今为止,最好的实验结果也只能达到486 kJ/m3[23].由于磁性能的实验结果与理论值之间存在很大差距,研究者采用各种理论模型及数值模拟对硬磁/软磁交换弹性薄膜进行研究,试图找到产生差距的原因,得到了一些定性甚至定量结果.
T. Leineweber等[12,49]计算了Nd2Fe14B/α-Fe磁性三层膜的剩磁随软磁相厚度的变化曲线,以及成核场、最大磁能积随软磁相厚度变化的曲线,并将成核场随软磁相厚度的变化趋势分为3个区间,随着软磁相厚度的增加,成核场先后经历平台、急速降低和缓慢降低3个区间.
G. P. Zhao等[9-11,29]经过详细分析发现以上的平台区间并不存在,并进一步指出复合磁体的磁化反转一般要经历反向磁畴的成核、反向磁畴的扩展和磁化矢量的不可逆翻转.计算表明:随着软磁层厚度的增加,矫顽力的机制从成核变为钉扎,并在此基础上提出了自钉扎的矫顽力机制和成核钉扎二重性的反磁化机制[29],这一理论得到了S. Sawatzki等[50]实验的证明.文献[51-54]还分析了Nd2Fe14B/α-Fe复合磁性材料实现最大磁能积的薄膜厚度,认为在硬软磁相厚度均为10 nm左右可以实现最大磁能积约为800 kJ/m3,并考虑了易轴取向对复合磁多层膜磁性能的破坏作用.
J. S. Jiang等[13-14,55]通过实验及理论分析得到了在一定程度上提高磁能积的方法,比如利用制作工艺改变界面的结构,致使界面的耦合强度增大,从而提高材料的磁能积.G. Asti等[7-8,56-60]计算了磁晶易轴平行和垂直于膜面的交换耦合纳米复合材料的磁相图,将磁体分为刚性复合磁体(RM)、交换弹簧磁体(ES)和退耦合磁体(DM),得到了不同材料的软磁相和硬磁相的最佳比例,推导出易轴垂直于膜面情况下的钉扎场公式,并分析了界面交换耦合强度对磁滞回线的影响.
近年来,实验上也对交换弹簧进行了很多研究[45,61-71],磁能积得到很大提高,其中,关于硬磁软磁多层膜的文献很多.研究发现,相比于块材,薄膜材料的晶体易轴和材料的均匀性都比较容易控制,可以得到较高的磁能积.此外,现代技术可以较容易地掌控薄膜厚度,其实验结果可以很方便地与理论进行对比,据此可以分析薄膜厚度对磁性能特别是矫顽力机制的影响.2011年,S. Sawatzki[50]等通过在软磁相Fe磁层中加入少量Co来提高SmCo5/Fe三层膜的磁性能,其最大磁能积可达到39 MGOe.2012年,W. B. Cui等[23]通过在界面加入很薄的非磁性Ta层对硬磁相和软磁相的元素进行隔离,合成的Nd2Fe14B/FeCo的磁能积达到了61 MGOe.A. M. Belemuk等[72-73]还研究了温度对磁性能的影响.
微磁学最重要的任务之一是计算磁滞回线,从磁滞回线上可以比较不同磁性材料的磁性能特别是矫顽力.矫顽力是表征材料在磁化以后保持磁化状态能力的大小,是考察永磁材料的标准之一,也是划分软磁和永磁材料的依据[24].目前复合磁体微磁学计算理论和实验的主要差距就是在矫顽力方面,理论计算的矫顽力比实验大很多,导致理论计算的磁能积偏大.这一差距几乎在所有材料中都存在,基于此W. F. Brown[74-75]提出了矫顽力悖论.这一悖论产生的根本原因是理论计算一般都忽略了某些细节,比如说材料的缺陷、微结构和温度等,这些细节往往会对矫顽力造成致命的破坏.
本文通过比较的方法主要讨论3种微磁学方法及其优缺点:一维全解析模型、一维半解析模型以及三维数值模拟计算3种方法.通过细致的比较,对现有理论取得的成绩和存在的问题作较为系统的综述,并讨论理论和实验结果存在差别的原因.
一维全解析模型[18,76-77]的优点在于公式和推导过程都很简单,具有清晰的物理意义,特别是可以清楚地给出材料的矫顽力机制,对磁化物理过程有合理的解释.但是这种模型往往只考虑了磁晶各向异性能和外场能,忽略了磁矩之间的相互作用,只能粗略地描述磁化反转过程,得到的矫顽力和磁能积与实验结果相差很大.
与以上简单模型相反,许多数值模拟软件可以实现较为复杂的微磁学模拟,如利用有限元法(FEM)的Nmag、Magpar和Ansys等软件,以及利用有限差分法(FDM)的OOMMF和Matlab等软件.有限元法适用于非立方体结构磁性材料的模拟计算,H. Kronmüller等[78-79]利用这种方法模拟了Nd2Fe14B/α-Fe和Pr2Fe14B/Fe纳米复合材料的磁滞回线;M. Yue等[80-81]也运用有限元方法计算了MnBi/Fe复合磁体的磁滞回线.G. P. Zhao等[82-85]则运用OOMMF软件计算了Nd2Fe14B/Fe2Co、Sm-Co/Fe以及Nd2Fe14B/Fe等材料的磁滞回线和磁矩自旋分布.通过求解Landau-Lifshitz-Gilbert方程的三维数值模拟方法可以得到磁矩分布随外场变化的三维动态过程,并进而求得磁滞回线.本文将重点讨论微磁学模拟中最常使用的软件OOMMF及其在复合材料微磁学计算中的应用.除了有限元和有限差分方法,还有其他方法来研究磁学性质,比如Monte Carlo方法,利用概率和随机性来计算磁矩的分布;原子链模型则是一维数值计算模型,其计算方法与以下讨论的一维半解析模型中的数值计算部分类似.数值计算可以模拟多种形状的磁性材料,但是也有一定局限性.由于磁畴壁里面的磁矩分布对磁滞回线有着重要影响,精确模拟磁畴壁是微磁学计算的一个重要任务,其网格大小要远小于畴壁宽度.稀土永磁体的畴壁都比较窄,一般在2~5 nm,因此划分的网格较多,计算量较大,需要高速度、大容量的计算机.
一维半解析模型[7-8,86-88]是介于三维数值计算和全解析模型之间的一种方法,它在简单和精确之间维持了一定的平衡,是硬磁/软磁复合磁体计算中用得最多的一种方法.它考虑了相邻磁矩之间的交换相互作用,通过公式推导,可以反映出磁化反转的物理过程.它计算量较小,适用于几何形状较为规则的体系如硬磁/软磁多层膜,能够比较准确地描述出不同外场下的磁化反转情况.与一维全解析模型相比,这种方法的解析推导要复杂得多,推导过程中有时需要进行简化处理,导致计算结果的精确程度下降.
以上理论研究可以从不同侧面很好地揭示硬磁/软磁多层膜的磁化反转机制.然而大多数的理论工作都具有一定的局限性,比如数值计算模型往往过于复杂,而且计算结果只是针对某种材料而言的,不具有普遍性.目前文献中对不同计算结果和计算模型进行比较和分析的工作相对较为缺乏.本文力图在这方面作一个综述,起到抛砖引玉的效果.下面从最简单的模型,即著名的S-W一致转动模型,讨论微磁学的计算方法,并分析磁滞回线产生的物理根源.
1一维全解析模型
1948年,E. C. Stoner和E. P. Wohlfarth[18]提出了一致转动模型(S-W模型).S-W模型假设磁性材料由微小晶粒构成并且每个晶粒都具有单易化轴,不考虑晶粒之间的相互作用,内部的磁化反转是通过一致转动实现的.该模型适用于单畴粒子,其自由能E只由磁晶各向异性能和塞曼能构成.对于较大的粒子或多晶粒子的磁化反转主要是通过磁畴壁的移动实现的,即畴壁移动模型[7,20-23],后者所得到的理论值更加接近实验值,但是更为复杂.这里主要讨论S-W模型.
1.1S-W模型根据S-W模型,能量密度公式可以写为
(1)
其中,K和Ms分别表示磁晶各向异性常数和饱和自发磁化强度,β表示磁晶易轴与外加磁场的夹角,通过对能量求极小值,即∂E/∂θ=0和∂E2/∂θ2>0就可以得到磁滞回线和矫顽力.
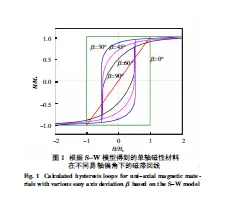
图1是根据S-W模型计算得到单轴磁性材料在不同易轴偏角下的磁滞回线.当β=0°时,对应的磁化强度只有2个稳定的态,即当外场等于临界场Hcrit的时候,磁化矢量就从M=+Ms直接跳转到M=-Ms,发生不可逆反转,得到的磁滞回线是方形的,此时矫顽力Hc=Hcrit=Hk=2K/Ms.在β=30°时,磁滞回线的方形度变差,剩磁和矫顽力都降低.在β=90°时,可以得到一条过原点的直线,没有形成磁滞回线.在β小于45°时,矫顽力大小等于临界场,矫矫力机制为钉扎,当β大于45°之后,矫顽力不再等于临界场.在外场小于临界场之前,磁化矢量都是可逆的,当外场大于临界场,磁矩将发生不可逆反转.根据S-W模型,取向的磁性材料矫顽力等于其各向异性场Hk,而各向同性材料(如甩带)的矫顽力为0.48Hk.对于磁王Nd2Fe14B来说,分别对应于6.7 T和3.3 T,而实验上烧结Nd2Fe14B和各向同性甩带Nd2Fe14B的矫顽力值一般在1~2 T,理论值比实验值大很多,跟W. F. Brown[74-75]提出的矫顽力悖论吻合.一般来说,S-W模型只能用于讨论单晶单畴粒子的矫顽力和磁滞回线,它可以使物理问题大大简化,并清楚地反映出矫顽力机制,将Hc与Hk紧密地联系起来.后来的研究发现,虽然S-W模型给出的矫顽力数值偏大,但是永磁材料的矫顽力和各向异性场Hk确实存在一个线性关系[28-29,89-91].
1.2一致转动模型的磁滞回线S-W模型一般适用于单畴粒子.实际上,热退磁态的单畴粒子在剩磁态往往不再是单畴粒子,所以严格地说一致转动模型在多数情况下并不适用,即使对于所谓的(在热退磁状态下的)单畴粒子也不适用[28-29].但是如上所述,一致转动模型作为一个近似模型具有清晰的物理意义,对实际的磁化反转过程也具有借鉴意义.基于此,G. P. Zhao等[76-77,92]将一致转动模型推广到硬/软磁复合材料并将一致转动模型的结果与更为精确的非一致转动模型进行比较,发现一致转动模型的成核场较高,对应一个不容易出现的成核模式.研究发现,当软磁相厚度较小时,一致转动模型给出的磁滞回线和非一致转动模型比较接近,可以粗略地反映磁化反转机制.
下面比较2种极端情况:一种是硬软磁之间完全退耦合,磁矩只随外场变化;第二种是硬软磁之间完全耦合,整个系统的磁矩随外场一致转动,如图2所示.
对硬/软磁复合材料,根据一致转动模型,总能量密度[24]可以写成
(2)
其中,右边的第一项为硬磁相的总能量密度,第二项表示软磁相的总能量密度,A表示交换作用常数,f是体积所占比例,上标h和s分别表示硬磁层和软磁层,θ是磁化矢量和外场方向的夹角.

由于多层膜体系具有周期性和对称性,因此多层膜可以看成双层膜的叠加,这里考虑硬/软磁双层膜体系,其性能可以推广到多层膜和三层膜体系.根据一致转动模型可以知道,在易轴和外场平行时矫顽力和临界场是相等的.由方程(2)可以得到矫顽力和临界场公式为
(3)
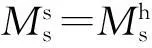
(4)
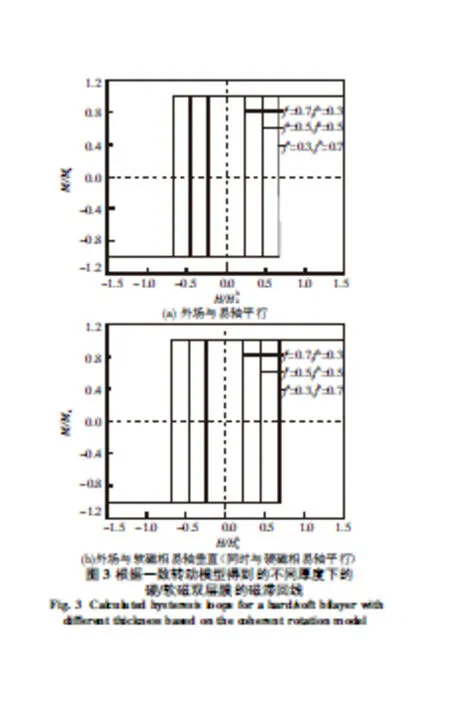
假设硬磁相和软磁相的磁晶各向异性差10倍,即λ等于0.1,代入(4)式可以计算出矫顽力并画出磁滞回线如图3所示.图3(a)表示外场与易轴平行时根据一致转动模型得到的不同厚度下的硬/软磁双层膜的磁滞回线,图3(b)表示外场与软磁相易轴垂直时(同时与硬磁相易轴平行)根据一致转动模型得到的不同厚度下的硬/软磁双层膜的磁滞回线.2种情况下,磁滞回线都是方形的并且主要的矫顽机制是成核.矫顽力随着软磁相厚度的增加而减小,垂直时的矫顽力比平行情况下的矫顽力要小,也就是说磁矩在易轴平行取向时比垂直取向时更容易反转.

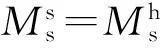
(5)
图4表示的是根据完全退耦合模型模拟得到的双层膜磁滞回线,其磁化状态有3种,即硬磁相磁矩和软磁相磁矩平行的状态、反平行状态和反向平行的状态.对应的退磁过程可以分为两部分:首先是软磁相磁矩的反转,对应磁化反转的成核过程;然后是硬磁相的磁矩反转,对应磁化反转的钉扎过程.这2个过程是完全独立的,在软磁相磁矩完全反转之后,硬磁相磁矩才开始偏转.软磁相与硬磁相的反转场分别等于各自的磁晶各向异性场.

利用以上简单模型,可以很容易推导出解析公式,得到矫顽力明确的物理意义及其随厚度的变化,在分析实验数据的时候有一定的参考价值.但是这2种模型都有一定的局限性,一致转动模型要求晶粒之间完全耦合,磁矩在磁化反转过程中磁矩矢量保持一致,而完全退耦合模型忽略了硬/软磁材料磁晶之间的相互作用,软磁相磁矩反转和硬磁相磁矩反转是独立完成的,这2种模型并不能精确描述出磁矩在反转过程中的分布,计算出的磁滞回线与实验差距也比较大.
2一维半解析模型
前面介绍了简单的一维全解析模型,接下来讨论一维半解析模型.H. Kronmüller等[79,86-87]、G. Asti等[7-8,56-60]以及G. P. Zhao等[88,92]运用这种模型研究了多种纳米复合材料的磁滞回线,并推导出成核场公式以及厚度较大时的钉扎场公式.本文以外场和易轴取向平行,并且均在薄膜平面内的情况为例,系统分析硬磁软磁多层膜磁体在退磁过程中的特点.薄膜的横向尺寸比其厚度大很多,因此可以假设膜面无限延伸,磁矩保持在膜面内偏转,静磁相互作用可以忽略不计.同时该模型假设磁矩在薄膜平面内一致转动,即磁矩只在厚度方向有一个分布,以便将退磁问题简化成为一维模型[7,9,12,93-94],通过解析分析来处理.根据W. F. Brown[95]的微磁学理论,易轴平行于膜面的三层膜体系的能量密度可以表示为
(6)
易轴垂直于膜面时的总能量密度则表示为
(7)
右边的第一项能量表示交换能,后面两项分别表示磁晶各向异性能和塞曼能,垂直时多了一项退磁能.这里的A、K和Ms分别表示交换作用常数、磁晶各向异性常数和饱和自发磁化强度,上标h和s分别代表硬磁相和软磁相,θ表示磁化矢量和外场方向的夹角.
系统的边界条件[8,88]为:
(9)
将(6)式代入欧拉方程,可以得到θ与z之间的关系:
其中,Δ=π(A/K)1/2表示材料的布洛赫宽度,Hk=2K/Ms表示磁晶各向异性场,h=H/Hk表示约化外场.
体系的边界条件为
将(10)和(11)式代入上面公式,边界条件可以改写成
(12)
在三层膜中,硬磁相所占的比例为2th/(ts+2th);而在多层膜中,硬磁相所占的比例为th/(ts+th).对三层膜来说,考虑到真空磁矩为零,体系的边界条件为
在多层膜中,考虑到对称性,也可以得到同样的体系边界条件
因此三层膜体系中硬磁相的厚度th可以对应多层膜中的2th.一个硬磁相厚度为th的三层膜,其磁滞回线和一个硬磁相厚度为2th的多层膜相同.因此,多层膜最大磁能积所对应的厚度是三层膜的2倍.而一个软磁相厚度为ts的双层膜则与一个软磁相厚度为2ts的三层膜对应,因此,三层膜最大磁能积所对应的厚度是双层膜的2倍.
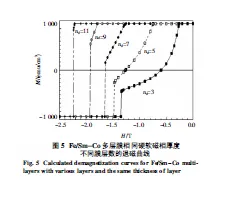
图5表示的是运用一维半解析方法得到Fe/Sm-Co相同硬软磁相厚度不同膜层数的退磁曲线[96](其总层数N=Nh+Ns=200,对于nd=3表示h/s/h三层膜;nd=5表示h/s/h/s/h五层膜).可以看到这种材料的退磁过程,从图中可以分析出成核场、矫顽力和钉扎场的变化.对于nd=11,磁滞回线接近于矩形,此时磁体为刚性磁体;nd=7,对应的磁体为交换弹簧磁体;nd=3,对应的磁体为退耦合磁体.一维解析微磁学方法可以有效解决一些物理问题,比如给出一维畴壁.但是这种分析方法有一定的局限性,由于数学表达式的复杂性,在推导过程中需要采取一些近似的方法,这可能导致计算结果误差较大.另外,这种方法适用范围受到一定限制,对于圆柱形、线形和锥形等形状计算起来较为困难.
3三维模型
三维数值模拟在过去十多年发展迅速,用这种方法可以模拟不同的磁体形状,比如薄膜、球体、圆柱体等,甚至不规则的形状,比如锥形体、线形等[97].对于较为复杂的不规则形状磁体,用三维数值模拟方法处理更为方便.R.P.Boardman等[98-101]用这种方法研究了不同形状的磁体磁化反转过程,G.P.Zhao等[82-84]用三维有限差分方法研究了纳米复合磁体退磁过程中,磁矩形成的形态以及磁滞回线和磁能积.这种三维微磁学计算方程是基于LLG[102]动力学方程
(13)

(14)
平均能量密度E可以用布朗方程[95]得到
(15)
A和K分别表示交换常数和磁晶各向异性常数,H表示外加磁场,Hd(r)表示退磁场.

G.P.Zhao等[82-84]成功地应用以上方法计算了易轴平行和垂直于膜面的磁滞回线,并与一维模型计算结果进行了细致比较.图7表示Nd2Fe14B/α-Fe双层膜易轴平行于膜面不同软磁相厚度的磁滞回线[83],其中上半部分由三维模拟计算得出,下半部分则根据一维半解析方法得到.由图7可见,二者符合得很好,证明了计算方法和结果的可靠性.在软磁相厚度很小的时候,磁滞回线为矩形,对应的复合磁体可以看成是刚性磁体,在厚度处于中间值时,磁滞回线的矩形度比刚性磁体差,此时表现出交换弹簧行为,对应的复合磁体磁相是交换弹簧.继续增大ts,成核场与钉扎场明显分离开来,对应的复合磁体磁相从交换弹簧过渡到退耦合.G.Asti等[7-8]的一维计算也给出了类似的结果.

其他材料的计算也得到了类似的结果.图8[84]是易轴垂直于膜面时,不同软磁相厚度下的Sm-Co/α-Fe三层膜的磁滞回线.图中实线是三维微磁学模拟得到的结果,虚线是一维模拟计算的结果.垂直取向与平行取向变化相似,随着软磁相厚度ts的增大,对应的复合磁体磁相从刚性到交换弹簧最后过渡到退耦合.在图中,可以发现三维数值模拟结果和一维解析计算结果很相近,只有在软磁相厚度比较大的时候差距才比较大,成核场和矫顽力都随着软磁相厚度的增加而减小.
4薄膜厚度对磁滞回线的影响
4.1软磁相厚度对磁滞回线的影响薄膜厚度特别是软磁相厚度对磁滞回线有着比较大的影响,随着软磁相厚度的增加,使得磁滞回线的方形度变差,导致磁能积急剧地减小,T.Leineweber等[12]、E.E.Fullerton等[105-108]以及G.Asti等[7-8]对此进行了深入研究.

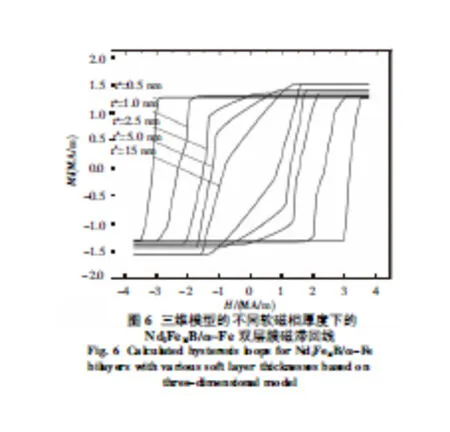
图9中描述的是外场垂直于膜面时不同软磁相厚度下Fe/FePt双层膜的磁滞回线[8].单相永磁体(软磁相厚度为零)的磁滞回线是一个矩形.随着软磁相厚度的增加,磁滞回线的方形度急剧下降,矫顽力也开始降低.在软磁相厚度很小的时候,成核场和钉扎场之间的间隙很小,磁滞回线接近方形,成核和磁矩的完全偏转几乎在同一外场下完成,此时矫顽力机制主要以成核为主,对应的磁体为刚性复合磁体.在软磁相厚度较大的时候,矫顽力机制以钉扎为主.随着软磁相厚度的增加,磁滞回线的方形度逐渐变差,成核场和矫顽力逐渐分离.当软磁相厚度较大时,畴壁扩展过程变长,因此成核到钉扎的历程变长,因此磁滞回线的方形度和磁能积都下降.同时,软磁相厚度的增加会导致矫顽力迅速降低;另一方面,如果软磁相厚度太小,杂质的影响会较大,导致矫顽力和磁能积降低.
4.2硬磁相厚度的影响硬磁相厚度对磁滞回线的影响相对较小,仅在厚度比较小的时候影响比较明显.图10给出了不同硬磁相厚度下Nd2Fe14B/α-Fe三层膜的磁滞回线[109],计算中软磁相厚度为80nm.
由于软磁层比较厚,图中的几个磁滞回线与图4类似,表现出明显的退耦合行为.在图10(a)中选取的硬磁相厚度较小,由于软磁相厚度远大于硬磁相厚度,磁滞回线的主要贡献来自于软磁相的磁矩偏转,此时磁滞回线的主导矫顽力机制是成核,随着硬磁相厚度的增大,成核场没有变化,钉扎场逐渐增大.在图10(b)中硬磁相厚度较大,随着硬磁相厚度的增加,成核场和钉扎场均没有变化,但是磁滞回线的主要贡献由软磁相的偏转逐渐过渡到硬磁相的偏转,矫顽力与成核场的差距逐渐增大,矫顽力机制从成核过渡到钉扎.

5易轴取向的影响
由R.Skomski和J.M.D.Coey两位科学家提出的理论磁能积是基于易轴与外加磁场方向完全一致的一维模型,并且要求软磁相材料结构无缺陷.在实际的磁性材料中,硬磁相和软磁相的易轴与外场都存在一定的夹角.在实验[45,110]中发现,当外场为零时,磁性材料的磁矩并不完全垂直或者平行于膜面,而是出现了一定的分布,也就是说磁晶易轴与外加磁场不会完全平行,而是存在一定的夹角.很多的理论计算都没有考虑磁晶易轴的有效偏角[60,88],因此这是磁能积实验值小于理论计算值的一个重要原因.

图11给出了th=10nm,ts=20nm易轴在膜面内不同β值下的Nd2Fe14B/α-Fe/Nd2Fe14B三层膜的退磁曲线[51].从这些曲线中不难看出,β对于磁滞回线有着很大的影响,随着β的增加磁滞回线变得越来越倾斜,剩磁也急剧减小.当外场为零时,由布朗方程可以知道,薄膜内部磁矩的方向与易轴的方向保持一致,剩磁可以表示为Ms=Mr×cosβ,M随着β的增大而减小.当M为零时,对应外场的相反数是矫顽力Hc,表征磁体抵抗退磁能力的大小.从图中可以看出,矫顽力随着β的增大而减小,当β等于0时,矫顽力机制为钉扎,随着β的增加,矫顽力小于钉扎场并且二者的差距逐渐增大.文献[52-54]也给出了类似结果.由于磁晶易轴偏角的存在,导致剩磁和矫顽力比理想情况小,引起磁能积的减小,在一定程度上解释了磁能积的理论值和实验值之间的巨大差距.
6理论和实验的对比
微磁学长期以来一直为部分人所诟病,主要原因在于理论计算给出的矫顽力和磁能积比实验大很多,这其实不是微磁学本身的问题.一方面,理论计算采取的模型过于简化;另一方面实验制造出的材料还有很多缺陷,这一差距较好地反映在W.F.Brown[74-75]提出的矫顽力悖论和G.P.Zhao等[9]提出的磁能积悖论中.G.P.Zhao等[28-29,89-91]进一步指出,随着实验手段的不断丰富和计算条件的不断改善,微磁学理论和实验的差别越来越小.图12给出了纳米复合材料Nd2Fe14B/Fe65Co35多层膜磁滞回线[111]最新的理论和实验对比.理论计算所选取的参数根据实验条件所确定.从图12可以看出理论得到的结果与实验结果比较接近,特别是理论得到的剩磁和矫顽力都和实验值差别不大.这也比较有力地证明了微磁学的可信度.

7讨论和结论
微磁学可以用来研究硬/软磁复合材料的磁滞回线,是比较有力且值得信赖的研究方法.本文中分别讨论了一维全解析、一维半解析以及三维数值模拟得到的磁滞回线,简单地介绍了这3种方法的优点以及缺点.在用一维全解析和三维数值模拟这种模型时,它可以明确给出磁化反转过程,尤其是畴壁的形成、扩展和钉扎.充分模拟畴壁的扩展,可以发现材料的矫顽力机制为自钉扎.而材料本身也存在各种杂质和缺陷,因此,修复材料本身缺陷和阻碍畴壁的扩展是提高矫顽力的2种有效方法.对复合磁体三维数值计算来说,最重要的是网格的选取.一个永磁体的磁畴壁的宽度大约是3~5nm.因此,网格尺寸应小于1nm×1nm×1nm,这样在每个单元内有着36°~60°的畴壁变化.这样的精度对取向的复合磁多层膜来说基本可以满足要求.由此,一个100nm×100nm×100nm的计算模型,需要106个网格,这个数量也是一台计算机的计算极限.有些时候,三维计算并不是最适合的,而一维解析方法可以取得更好的结果,总的来说,在计算能力受限的情况下,将一维和三维计算结合起来并将计算结果细致比较,取长补短,是一个较好的方法.
由以上讨论可知:矫顽力的降低是引起复合磁

体磁能积减小的一个重要原因.因此,G.P.Zhao等[85]提出,在实验上可以通过提高矫顽力来提高磁能积,比如在硬/软磁材料之间添加一层非铁磁层材料来避免两相材料在界面的扩散,从而提高材料的矫顽力.日本的K.Hono小组[23]和中国燕山大学的张湘义小组[112]用不同方法提高了界面的钉扎,在这方面取得了成功.磁性材料的易轴取向也会导致剩磁和磁能积迅速减小[52-54,111],控制好薄膜的易轴取向和材料的均匀性都可以提高磁能积.此外,较好地掌控薄膜厚度,也是提高磁能积的途径之一[7-8,12,105-108].
本文讨论了硬/软磁相厚度对磁滞回线的影响,分析了矫顽力和成核场的变化.可以得到软磁相厚度的增加会使得磁滞回线的方形度变差,矫顽力也逐渐降低,矫顽力机制逐渐从成核向钉扎过渡.由于软磁相厚度较大时,畴壁扩展过程变长,成核到钉扎的历程变长,导致磁滞回线的方形度和磁能积都下降.随着硬磁相厚度的增加,矫顽力与成核场的差距逐渐增大,矫顽力机制从成核过渡到钉扎,此时钉扎场的大小主要由硬磁相决定.除此之外,也讨论了磁晶易轴的取向对磁滞回线的影响,当易轴偏离逐渐增大,磁滞回线的方形度严重受损.体系的剩磁单调减小,矫顽力也呈减小的趋势,这是磁能积实验值比理论值小很多的一个重要原因.
参考文献
[1] COEHOORN R, DEMOOIJ D B, DEWAARD C. Meltspun permanent magnet materials containing Fe3B as the main phase[J]. J Magn Magn Mater,1989,80(1):101-104.
[2] COEHOORN R, DEMOOIJ D B, DUCHATEAU J, et al. Novel permanent magnetic materials made by rapid quenching[J]. J de Physique,1988,49(C-8):669-670.
[3] KNELLER E F, HAWING R. Exchange-spring magnet:a new material principle for permanent magnets[J]. IEEE Trans Magn,1991,27(4):3588-3591.
[4] SKOMSKI R, COEY J. Giant energy product in nanostructured two-phase magnets[J]. Phys Rev,1993,B48(21):15812-15816.
[5] LIU W, ZHANG Z D, LIU J P, et al. Exchange coupling and remanence enhancement in nanocomposite multilayer magnets[J]. Adv Mater,1993,14(24):1832-1834.
[6] LIU W, ZHANG Z D, LIU J P, et al Nanocomposite (Nd,Dy)(Fe,Co,Nb,B)5.5/α-Fe multilayer magnets with high performance[J]. J Phys D:Appl Phys,2003,36(17):L63-L66.
[7] ASTI G, SOLZI M, GHIDINI M, et al. Micromagnetic analysis of exchange-coupled hard-soft planar nanocomposites[J]. Phys Rev,2004,B69:174401.
[8] ASTI G, GHIDINI M, PELLICELLI R, et al. Magnetic phase diagram and demagnetization processes in perpendicular exchange-spring multilayers[J]. Phys Rev,2006,B73:094406.
[9] ZHAO G P, WANG X L. Nucleation, pinning, and coercivity in magnetic nanosystems:an analytical micromagnetic approach[J]. Phys Rev,2006,B74:012409.
[10] ZHAO G P, CHEN L, HUANG C W, et al. Micromagnetic calculation of hysteresis loops in exchange-coupled nanolayers[J]. Solid State Commun,2010,150(31):1486-1488.
[11] ZHAO G P, ZHOU G, ZHANG H W, et al. Angular dependence of magnetic reversal in two-phased nanolayers[J]. Comput Mater Sci,2008,44(1):117-121.
[12] LEINEWEBER T, KRONMÜLLER H. Micromagnetic examination of exchange coupled ferromagnetic nanolayers[J]. J Magn Magn Mater,1997,176(97):145-154.
[13] JIANG J S, PEARSON J E, LIU Z Y, et al. Improving exchange-spring nanocomposite permanent magnets[J]. Appl Phys Lett,2004,85(22):5293-5295.
[14] CHOI Y, JIANG J S, PEARSON J E, et al. Controlled interface profile in Sm-Co/Fe exchange-spring magnets[J]. Appl Phys Lett,2007,91(7):072509-3.
[15] SAWATZKI S, HELLER R, MICKEL Ch, et al. Largely enhanced energy density in epitaxial SmCo5/Fe/SmCo5exchange spring trilayers[J]. J Appl Phys,2011,109(12):123922-7.
[16] BELEMUK A M, CHUI S T. Comparative study of finite temperature demagnetization in Nd2Fe14B and SmCo5based hard-soft composites[J]. J Appl Phys,2011,110(7):073918-7.
[17] BELEMUK A M, CHUI S T. Temperature-dependent demagnetization behaviour in perpendicular exchange-coupled SmCo5/FeCo multilayers[J]. J Phys D:Appl Phys,2012,45(12):125001-125014.
[18] STONER E C, WOHLFARTH E P. A mechanism of magnetic hysteresis in heterogeneous alloys[J]. Magnetics,Phil Trans Roy Soc London,1948,A240:599-642.
[19] NÉEL L. Les lois de l’aimantation et de la subdivision en domaines élémentaires d'un monocristal de fer[J]. J Phys Radium,1944,5(11):265-276.
[20] ZHAO G P, ZHAO M G, LIM H S, et al. From nucleation to coercivity[J]. Appl Phys Lett,2005,87(16):162513-3.
[21] ZHAO G P, CHEN L, HUANG C W, et al. Evolution of domain walls and reversal mechanism in exchange-coupled nanolayers[J]. J Magn Magn Mater,2009,321(15):2322-2326.
[22] ATKINSON D, ALLWOOD D A, XIONG G, et al. Magnetic domain-wall dynamics in a submicrometre ferromagnetic structure[J]. Nature Material,2003,2(2):85-87.
[23] CUI W B, TAKAHASHI Y K, HONO K. Nd2Fe14B/FeCo anisotropic nanocomposite films with a large maximum energy product[J]. Adv Mater,2012,24:6530-6535.
[24] 姜寿,李卫. 凝聚态磁性物理[M]. 北京:科学出版社,2003:344.
[25] ARCAS J, HERNANDO A, BARANDIARn J, et al. Soft to hard magnetic anisotropy in nanostructured magnets[J]. Phys Rev,1998,B58(9):5193-5196.
[26] FENG W C, GAO R W, YAN S S, et al. Effects of phase distribution and grain size on the effective anisotropy and coercivity of nanocomposite Nd2Fe14B/α-Fe magnets[J]. J Appl Phys,2005,98(4):044305-5.
[27] HAN G B, GAO R W, FU S, et al. Effective anisotropy between magnetically soft and hard grains in nanocomposite magnets[J]. Appl Phys,2005,A81(3):579-582.
[28] ZHAO G P, MORVAN F, WAN X L. Micromagnetic calculation for exchange-coupled nanocomposite permanent magnets[J]. Rev Nanosci Nanotechnol,2014,3(4):227-258.
[29] ZHAO G P, ZHANG X F, MORVAN F. Theory for the coercivity and its mechanisms in nanostructured permanent magnetic materials[J]. Rev Nanosci Nanotechnol,2015,4:1-25.
[30] JULLIERE M. Tunneling between ferromagnetic films[J]. Phys Lett,1975,A54(3):225-226.
[31] SLONCZEWSKI J C. Conductance and exchange coupling of two ferromagnets separated by a tunneling barrier[J]. Phys Rev,1989,B39(10):6995-7002.
[32] GIEBELER C, ADELERHOF D J, KUIPER A E T, et al. Robust GMR sensors for angle detection and rotation speed sensing[J]. Sensors and Actuators,2001,A91(1):16-20.
[33] DAUGHTON J M. GMR and SDT sensor applications[J]. IEEE Trans Magn,2000,36(5):2773-2778.
[34] CHRISTIDES C, STAVROYIANNIS S, KALLIAS G, et al. Giant magnetoresistance Co/Cu multilayer sensors for use in magnetic field mapping[J]. Sensors and Actuators,1999,A76(1):167-171.
[35] SHENG L, XING D Y, SHENG D N, et al. Theory of colossal magnetoresistance in R1-xAxMnO3[J]. Phys Rev Lett,1997,79(9):1710-1713.
[36] MILLIS A J, LITTLEWOOD P B, SHRAIMAN B I. Double exchange alone does not explain the resistivity of La1-xSrxMnO3[J]. Phys Rev Lett,1995,74(25):5144-5147.
[37] WARREN E P, DAVID J S. Electronic structure and half-metallic transport in the La1-xCaxMnO3system[J]. Phys Rev,1996,B53(3):1146-1160.
[38] LI X W, GUPTA A, XIAO G, et al. Low-field magnetoresistive properties of polycrystalline and epitaxial perovskite manganite films[J]. Appl Phys Lett,1997,71(8):1124-1126.
[39] HWANG H Y, CHEONG S W, ONG N P, et al. Spin-polarized intergrain tunneling in La2/3Sr1/3MnO3[J]. Phys Rev Lett,1996,77(2):2041-2044.
[40] SCHIFFER P, RAMIREZ A P, BAO W, et al. Low temperature magnetoresistance and the magnetic phase diagram of La1-xCaxMnO3[J]. Phys Rev Lett,1995,75(18):3336-3339.
[41] GRIFFITHS M K, BISSHOP J E L, DAVIES H A. Computer simulation of single-phase nanocrystalline permanent magnets[J]. J Magn Magn Mater,1999,183(1):49-67.
[42] 王博文,葛景岩. 巨磁致伸缩材料及其应用[J]. 沈阳工业大学学报(自然科学版),1998,20(3):64-67.
[43] CLARK A E, WUN-FOGLE M, RESTORFF J B, et al. Magnetostriction and magnetomechanical coupling of grain oriented Tb0.6Dy0.4sheet[J]. IEEE Trans Magn,1993,29(6):3511-3513.
[44] DUC N H, MACKAY K, BETZ J, et al. Giant magnetostriction in amorphous (Tb1-xDyx)(Fe0.45Co0.55)yfilms[J]. J Appl Phys,1996,79(2):973-977.
[45] ZHANG J, TAKAHASHI Y K, GOPALAN R, et al. Sm(Co,Cu)5/Fe exchange spring multilayer films with high energy product[J]. Appl Phys Lett,2005,86(12):122509-3.
[46] YUE M, ZHANG J, TIAN M. Microstructure and magnetic properties of Isotropic bulk NdxFe94-xB6(x=6,8,10) nanocomposite magnets prepared by spark plasma sintering[J]. J Appl Phys,2006,99(8):08B502-3.
[47] ZHANG J, LI Y X, WANG F, et al. Coercivity mechanism of nanocomposite Sm-Co/Fe multilayer films[J]. J Appl Phys,2010,107(4):043911.
[48] LIU W Q, ZUO J H, YUE M, et al. Strucure and magnetic properties if bulk anisotropic SmCo5/α-Fe nanocomposite permanent magnets with different α-Fe content[J]. J Appl Phys,2011,109(7):07A741-3.
[49] LEINEWEBER T, KRONMÜLLER H. Magnetization reversal modes in inhomogeneous magnets[J]. Phys Stat Sol,1997,201(1):291-301.
[50] SAWATZKI S, HELLER R, MICKEL C, et al. Largely enhanced energy density in epitaxial SmCo5/Fe/SmCo5exchange spring trilayers[J]. J Appl Phys,2011,109(12):123922-7.
[51] XIA J, ZHAO G P, ZHANG H W, et al. Significant deterioration of energy products in exchange-coupled composite magnets[J]. J Appl Phys,2012,112(1):013918-5.
[52] 夏静,张溪超,赵国平. 易轴取向对Nd2Fe14B/α-Fe双层膜退磁过程影响的微磁学分析[J]. 物理学报,2013,62(22):227502.
[53] 夏静,赵国平,张敏,等. 易轴取向对硬/软磁多层膜磁性能的影响[J]. 中国科学:物理学·力学·天文学,2013,43(1):39-47.
[54] WAN X L, ZHAO G P, ZHANG X F, et al. Hysteresis of misaligned hard-soft grains[J]. J Magn Magn Mater,2016,397:181-187.
[55] GUO Z J, JIANG J S, PEARSON J E, et al. Exchange-coupled Sm-Co/Nd-Co nanomagnets:correlation between soft phase anisotropy and exchange field[J]. Appl Phys Lett,2002,81(11):2029-2031.
[56] ASTI G, CARBUCICCHIO M, RATEO M, et al. Exchange coupling in nanometric Fe/Co multilayers[J]. J Magn Magn Mater,1999,59:196-197.
[57] GHIDINI M, ASTI G, PELLICELLI R, et al. Hard/soft composite magnets[J]. J Magn Magn Mater,2007,316(11):159-165.
[58] ASTI G, CARBUCICCHIO M, GHIDINI M, et al. Microstructural and magnetic properties of exchange-coupled Co/Fe multilayers[J]. J Appl Phys,2000,87(9):6689-6691.
[59] ASTI G, GHIDINI M, NERI F M, et al. Flux reversal in hard-soft composite magnets[J]. J Magn Magn Mater,2004,272(2):650-651.
[60] ASTI G, SOLZI M, GHIDINI M. Reversal modes of the multilayer exchange-spring magnet[J]. J Magn Magn Mater,2001,226/230:1464-1466.
[61] LIU Y G, XU L, WANG Q F, et al. Development of crystal texture in Nd-lean amorphous Nd9Fe85B6under hot deformation[J]. Appl Phys Lett,2009,94(17):172502-3.
[62] CHENG Z H, ZHANG J X, KRONMüLLER H. Magnetically soft phase in magnetization reversal processes of nanocomposite Sm2Fe15Ga2Cx/α-Fe permanent magnetic materials[J]. Phys Rev,2003,B68(14):144417.
[63] LI W, LI L L, NAN Y, et al. Controllable nanocrystallization in amorphous Nd9Fe85B6via combined application of severe plastic deformation and thermal annealing[J]. Appl Phys Lett,200,91(6):062509-3.
[64] GABAY A M, ZHANG Y, HADJIPANAYIS G C. Die-upset hybrid Pr-Fe-B nanocomposite magnets[J]. Appl Phys Lett,2004,85(3):446-448.
[65] LEE D, BAUSER S, HIGGINS A, et al. Bulk anisotropic composite rare earth magnets[J]. J Appl Phys,2006,99(8):08B516-3.
[66] LIU J P, LUO C P, LIU Y, et al. High energy products in rapidly annealed nanoscale Fe/Pt multilayers[J]. Appl Phys Lett,1998,72(4):483-485.
[67] LI B Z, ZHANG M, SHEN B G, et al. Non-uniform magnetization reversal in nanocomposite magnets[J]. Appl Phys Lett,2013,102(10):102405-4.
[68] YAO Q, LIU W, CUI W B, et al. Growth mechanism and magnetic properties for the out-of-plane-oriented Nd-Fe-B films[J]. J Mater Res,2009,24(9):2802-2812.
[69] GOLL D, BREITLING A, GU L, et al. Experimental realization of graded L10-FePt/Fe composite media with perpendicular magnetization[J]. J Appl Phys,2008,104(8):083903-4.
[70] ZHOU T J, LIM B C, LIU B. Anisotropy graded FePt-TiO2nanocomposite thin films with small grain size[J]. Appl Phys Lett,2009,94(5):152505-3.
[71] PANDEY K K M, CHEN J S, CHOW G M, et al. L10CoPt-Ta2O5exchange coupled multilayer media for magnetic recording[J]. Appl Phys Lett,2009,94(23):232502-3.
[72] BELEMUK A M, CHUI S T. Comparative study of finite temperature demagnetization in Nd2Fe14B and SmCo5based hard-soft composites[J]. J Appl Phys,2011,110(7):073918.
[73] BELEMUK A M, CHUI S T. Temperature-dependent demagnetization behaviour in perpendicular exchange-coupled SmCo5/FeCo multilayers[J]. J Phys D:Appl Phys,2012,45(12):125001.
[74] BROWN W F. Theory of the approach to magnetic saturation[J]. Phys Rev,1940,58(8):736-743.
[75] BROWN W F. The effect of dislocation on magnetization near saturation[J]. Phys Rev,1941,60(2):139-147.
[76] ZHAO G P, WANG X L, FENG Y P, et al. Coherent rotation and effective anisotropy[J]. IEEE Trans Magn,2007,43(6):2908-2910.
[77] 李建明,郭乃理,李貌,等. 硬/软磁复合材料的一致转动模型及其磁滞回线[J]. 四川师范大学学报(自然科学版),2013,36(2):263-268.
[78] FISCHER R, KRONMÜLLER H. Importance of ideal grain boundaries of high remanent composite permanent magnets[J]. J Appl Phys,1998,83(6):3271-3275.
[79] KRONMÜLLER H, GOLL D. Magnetic properties of exchange-spring composite films[J]. Solid State Physics,2011,248(10):2361-2367.
[80] LI Y Q, YUE M, ZUO J H, et al. Investigation of magnetic properties of MnBi/α-Fe nanocomposite permanent magnets by micromagnetic simulation[J]. IEEE Trans Magn,2013,49(7):3391-3393.
[81] LI Y Q, YUE M, ZUO J H, et al. Effect of α-Fe content on the magnetic properties of MnBi/α-Fe nanocomposite permanent magnets by micromagnetic calculation[J]. J Magn,2013,18(3):245-249.
[82] YUAN X H, ZHAO G P, YUE M, et al. 3D and 1D calculation of hysteresis loops and energy products for anisotropic nanocomposite films with perpendicular anisotropy[J]. J Magn Magn Mater,2013,343(5):245-250.
[83] ZHANG W, ZHAO G P, YUAN X H, et al. 3D and 1D micromagnetic calculation for hard/soft bilayers with in-plane easy axes[J]. J Magn Magn Mater,2015,324(24):4231-4236.
[84] ZHANG X C, ZHAO G P, XIA J, et al. Micromagnetic simulation of Sm-Co/α-Fe/Sm-Co trilayers with various angles between easy axes and the film plane[J]. Chin Phys,2014,B23(9):097504-7.
[85] SI W J, ZHAO G P, RAN N, et al. Deterioration of the coercivity due to the diffusion induced interface layer in hard/soft multilayers[J]. Scientific Reports,2015,5:16212.
[86] KRONMÜLLER H, GOLL D. Micromagnetic analysis of nucleation-hardened nanocrystalline PrFeB magnets[J]. Scripta Mater,2002,47(8):551-556.
[87] FISCHER R, KRONMüLLER H. Static computational micromagnetism of demagnetization processes in nanoscaled permanent magnets[J]. Phys Rev,1996,B54(10):7284-7294.
[88] ZHAO G P, DENG Y, ZHANG H W, et al. Accurate calculation of the nucleation field and hysteresis loops in hard-soft multilayers[J]. J Appl Phys,2011,109(7):07D340-3.
[89] YUE M, LI Y Q, WU Q, et al. Bulk nanostructural permanent magnetic materials[J]. Rev Nanosci Nanotechnol,2014,3(4):276-288.
[90] LIU W Q, YUE M, CUI B Z, et al. Permanent magnetic nanoparticles and nanoflakes prepared by surfactant-assisted high-energy ball milling[J]. Rev Nanosci Nanotechnol,2014,3(4):259-275.
[91] ZHANG J, YAN A R, LIU J P. Permanent magnetic films[J]. Rev Nanosci Nanotechnol,2014,3(4):289-303.
[92] ZHAO G P, YANG C, XIAN C W, et al. Analytical determination of nucleation field and magnetic reversal modes in exchange-coupled nanolayers[J]. Mod Phys Lett,2009,B23(25):2955-2961.
[93] PELLICELLI R, SOLZI M, NEU V, et al. Characterization and modeling of the demagnetization processes in exchange coupled SmCo5/Fe/SmCo5trilayers[J]. Phys Rev,2010,B81(18):184430.
[94] WILSON M, ZHU M, MYERS R, et al. Interlayer and interfacial exchange coupling in ferromagnetic metal/semiconductor heterostructures[J]. Phys Rev,2010,B81(4):045319.
[95] BROWN W F. Virtues and weaknesses of the domain concept[J]. Rev Mod Phys,1945,17(1):15-19.
[96] AMATO M, PINI M G, RETTORI A. Optimization study of the nanostructure of hard/soft magnetic multilayers[J]. Phys Rev,1999,B60(5):3414-3420.
[97] SKOMSKI R, LIU J P, SELLMYER D J. Quasicoherent nucleation mode in two-phase nanomagnets[J]. Phys Rev,1999,B60(10):7359-7365.
[98] ZZIMMERMANN J R P, BORDIGNON G, BOARDMAN R P, et al. Micromagnetic simulation of the magnetic exchange spring system DyFe2/YFe2[J]. J Appl Phys,2006,99(8):08B904-3.
[99] BOARDMAN R P, ZIMMERMANN J R P, FANGOHR H, et al. Micromagnetic simulation studies of ferromagnetic part-spheres[J]. J Appl Phys,2005,97(10):10E305-3.
[100] BOARDMAN R P, FANGOHR H, COX S J, et al. Micromagnetic simulation of ferromagnetic part-spherical particles[J]. J Appl Phys,2004,95(11):7037-7039.
[101] BOARDMAN R P. Computer simulation studies of magnetic nanostructures[D]. Southampton:University of Southampton,2005.
[102] DONAHUE M J, PORTER D G. OOMMF User’s Guide, Version 1.0[M/OL]. National Institute of Standards and Technology,1999. http://math.nist.gov/oommf/.
[103] FULLERTON E E, JIANG J S, BADER S D. Hard/soft magnetic heterostructures:model exchange-spring magnets[J]. J Magn Magn Mater,1999,200(1):392-404.
[104] CHEN B Z, ZHAO G P, ZHANG H W, et al. 3D calculation of hysteresis loops, magnetic orientations and reversal processes for exchange-spring bilayers with perpendicular anisotropy[J]. Physica,2012,B407:4574-4578.
[105] FULLERTON E E, JIANG J S, GRIMSDITCH M, et al. Exchange-spring behavior in epitaxial hard/soft magnetic bilayers[J]. Phys Rev,1998,B58:12193-12200.
[106] FULLERTON E E, JIANG J S, SOWERS C H. Structure and magnetic properties of exchange-spring Sm-Co/Co superlatices[J]. Appl Phys Lett,1998,72(3):380-382.
[107] JIANG J S, FULLERTON E E, GRIMSDITCH M, et al. Exchange-spring behavior in epitaxial hard/soft magnetic bilayer films[J]. J Appl Phys,1998,83(11):6238-6240.
[108] FULLERTON E E, SOWERS C H, PEARSON J E, et al. A general approach to the epitaxial growth of rare-earth-transition-metal films[J]. Appl Phys Lett,1996,69(16):2438-2440.
[109] ZHAO G P, DENG Y, ZHANG H W, et al. Thickness dependent magnetic reversal process and hysteresis loops in exchange-coupled hard-soft trilayers[J]. J Appl Phys,2010,108(9):093928-8.
[110] LIU Y, GEORGE T A, SKOMSKI R, et al. Aligned and exchange-coupled FePt-based films[J]. Appl Phys Lett,2011,99(17):172504-3.
[111] 彭懿,赵国平,吴绍全,等. 不同易轴取向下对Nd2Fe14B/Fe65Co35磁性双层膜的微磁学模拟[J]. 物理学报,2014,63(16):167505.
[112] LI H L, LOU L, HOU F, et al. Simulataneously increasing the magnetization and coercivity of bulk nanocomposite magnets via severe plastic deformation[J]. Appl Phys Lett,2013,103(14):142406.
(编辑李德华)
Review of Micromagnetic Theory for Hysteresis Loop of Nanocomposite Hard/Soft Permanent Magnets
ZHAO Guoping,WAN Xiulin
(CollegeofPhysicsandElectronicEngineering,SichuanNormalUniversity,Chengdu610066,Sichuan)
Abstract:Exchange-spring nanocomposite hard/soft magnets, as a new type of high-performance permanent magnets, has fundamental researches and applications and attracte much attention. This new kind of magnets with numerous magnetic properties and a giant especial magnetic energy product’has a theoretical upper limit of 1 MJ/m3. Micromagnetics as a bridge between the quantum magnetism and macroscopic magnetism, is an important theory to investigate the properties of magnetic materials and can clearly demonstrate the reversal mechanism of a given material as well as predicting its hysteresis loop and magnetic properties. This paper mainly expounds the hysteresis loops of thin film composite magnets according to three important micromagnetic calculation models: full analytical, quasi-analytical and numerical models. The advantages and weaknesses of each model are discussed. The results obtained from the three different models are compared and the effect of the hard/soft phase thicknesses and easy axis orientation on the macro hysteresis loops and coercivity mechanism are analysed. The gap between the theoretical and the experimental values are disscussed to propose some methods to enhance the magnetic properties of a given material, especially its coercivity and energy product.
Key words:micromagnetic; hysteresis loop; magnetic energy product
doi:10.3969/j.issn.1001-8395.2016.01.024
中图分类号:O482.5
文献标志码:A
文章编号:1001-8395(2016)01-0136-15
作者简介:赵国平(1967—),男,教授,主要从事纳米永磁材料、斯格明子、交换偏置和鸟类磁感应机制的研究,E-mail:zhaogp@uestc.edu.cn
基金项目:国家自然科学基金(10747007和11074179)
收稿日期:2015-11-10
