一类具非线性记忆的非线性阻尼波方程全局吸引子的存在性
2016-05-06蒲志林
李 婧, 蒲志林
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
一类具非线性记忆的非线性阻尼波方程全局吸引子的存在性
李婧,蒲志林*
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
摘要:研究一类具非线性记忆的非线性阻尼波方程全局吸引子的存在性,采用新的先验估计证明解半群S(t)是渐近紧的,从而证明该方程带有Dirichlet边界条件在H=H01(Ω)×L2(Ω)中吸引子是存在的.
关键词:全局吸引子; 非线性阻尼; 非线性记忆; 先验估计; 波方程
1引言与预备知识
设Ω⊂Rn是具有光滑边界Γ的有界区域,γ是正常数.考虑波方程
(1)
g(ut)是方程的非线性阻尼项,M(t-s)是方程的非线性记忆项,并且对任意的s属于R+,M(s)是单调递减的;f(u)是方程的非线性源项,满足次临界指数增长限制条件.
问题(1)描述的是具非线性记忆和非线性内部阻尼的粘弹性问题.研究人员对具线性和非线性记忆项的波方程做了大量研究工作[1-5],考虑非线性内部阻尼的情形.如果阻尼项g是线性的,其全局吸引子的存在性已被证明[6],本文通过对非线性内部阻尼项g的增长限制,证明此类问题是存在全局吸引子的.

(2)
特别地,V0=H,V1=V.当s1>s2时,有D(As1)D(As2)是紧嵌入,并且有[1,7]

(3)
C是仅依赖于n、Ω的常数,λ1是算子A的第一特征值.
假设非线性项f(u)及它的原函数
是满足下列条件的[7]:
(f2) |f′(s)|≤h1(1+|s|α),γ满足:


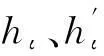
(4)
(5)
对非线性阻尼项g(ut)的假设[8]:
(g1) g∈C1(R),g(0)=0,g是严格递增的;
(g3) b1(|s|ν-b2)≤|g(s)|≤b3(1+|s|p),s∈R.
由(g3)和Young不等式可以得到
(6)
b是依赖于s的常数.
从(g1)和(g2)中可以推出
(7)
对记忆核M满足[1,4]:
(M1)M∈C1(R+)∩L1(R+);
(M2)M(s)≥0,M′(s)≤0,∀s∈R+;
(M4) 存在m1,m2>0,使得m1M≤M′≤m2M.
关于问题(1)的适定性,有如下结果.
定理 1.1[1,7,9]在以上假设条件下,对所有的t∈[0,T],-△u(t)+kg(ut(t))∈L2(Ω).初值
满足u0∈V,u1∈H,u(t)是方程(1)的唯一解,从而在H空间中有连续的半群(t)有:
定义 1.1设X是度量空间,S(t)是X中的半群,B是X的子集,如果X中的任意有界集B0,存在t1对任意的t≥t1(B0),使得S(t)B0⊂B,则B叫做S(t)在X中的吸收集.
定义 1.2[6,10]设X是一个完备的度量空间,A是X的有界子集,在X中非紧集的Kuratowski测度K定义如下:
K(A)=inf{δ|A有限开覆盖的半径≤δ}.
引理 1.1[6,9,10]在完备空间X中的非紧性测度K(A)有如下性质:

3)K(A+B)≤K(A)+K(B),对任意的A,B⊂X.
定理 1.2[6,10-11]设X是一个Banach空间,S(t)t≥0是X上的一个连续的半群,如果满足下列2个条件:
1)S(t)t≥0在X里有有界吸收集;
2) 对X中的任意有界子集有K(S(t)B0)→0,则S(t)在空间X存在全局吸引子.
2有界吸收集的存在性
由非线性记忆项的特点,可以记

(8)
则
(9)
并令
(10)
用v=ut+εu与方程(1)作内积:
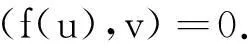
(11)
于是
由(8)~(10)式及以上计算可得
综上计算,(11)式可写作
由(g1)~(g3)可知
则上式可写作
(12)
式子里面的所有系数都为正数,取
记上述式子中对t求导部分为E1,则
故(12)式可写作
由(4)式可计算

故用Gronwall引理对任意的t≥0有
(13)

(14)
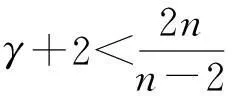
因此有H里的有界集B0,有S(t)B0⊂B,故
记
(15)
定理 2.1在空间H中,以0为中心μ为半径的球B(0,μ)是S(t)在H中半群S(t)的吸收集.对H中的任意有界集B0都存在t0>0,使得当t≥t0时有
t0和μ由(14)、(15)式给出.
3解半群S(t)的渐近紧性
用类似于文献[7-9,12]中对解进行分解的方法,把方程(1)的解u分解成

从而可以得到如下2个方程组:
引理 3.1[1,7]在(1)式的假设下,存在δ>0使得对任意的{u,ut}∈Cb(R+,H)有
更进一步的对任意给出的H中的有界集B,都存在C(B)>0使得如果u0,u1∈B有
证明这个引理的证明与文献[1]有类似的地方,但略有不同.
由(f2)有,n≥4时,f′(u)在L∞(Ω)上对任意的u∈H此结论都显然是成立的.
在n=3时,由Sobolev嵌入定理可以得到
从而进一步可以得到
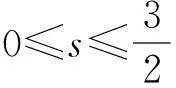
由(f2)可以得到

由Sobolev嵌入定理有
让ν(t)∈V1-δ2,则有
用Hölder不等式

由前面的条件易知C(B)是有界的,则
在V1-δ的对偶空间Vδ-1里,其范数在Vδ-1上也是有界的.所以此引理得证.
n=1,2时,对任意的q<∞有


引理 3.2[8-9]方程以u0,u1∈S(t)B为初值,对任意的ε>0,都存在时间
在前面一节已给出,有
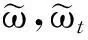
证明证明过程与文献[8-9]类似,再结合引理3.1即可证得.


证明参见文献[8].
定理 3.1[9]在度量空间H中,对任意的ε>0,有t1=t1(ε,B)使得
KH(S(t)B≤Cε
对所有的t≥t1成立.C是依赖于ε和t1的常数.
证明方法与文献[9]类似.
对任意的t1≥T=T(ε,B,t0),t0在前一节已经给出,可以把方程(1)的解分解成如下形式:
于是
由引理3.2可以得到,方程以u0,u1∈S(t1)B为初值,对任意的ε>0,存在时间T(上面已经给出),在t≥T时有
再结合引理1.1,即可得到
C只依赖于时间t0、t1和ε.于是定理得证.
最后由定理2.1和定理3.1即可证方程(1)满足定理1.2,有如下定理.
定理 3.2对满足条件(f1)~(f3),(g1)~(g3)和(M1)~(M4)的方程(1),在
中存在全局吸引子.
参考文献
[1] HAN Y H, YU Z G, JIN Z G. Global attractors for damped wave equation with nonlinear memory [J]. J Math Res Appl,2012,32(2):213-222.
[2] ZHU C S. Existence of global attractors for wave equation of kirchhoff type with nonlinear damping and memory term at boundary[J]. Dynam PDE,2007,4(3):247-262.
[3] PATA V. Attractors for a damped wave equation onR3withlinearmemory[J].MathMethApplSci, 2000,23(7):633-65.
[4] FEI L, GAO H J. Global existence and blow-up of solutions for a nonlinear wave equation with memory[J]. J Inequal Appl,2012,2012(1):1-27.
[5] 罗宏. Chemotaxis-Growth 系统的整体吸引子[J]. 四川师范大学学报(自然科学版),2010,33(5):577-580.
[6] HALE J K. Asymptotic Behavior of Dissipative Systems[M]. Providence:Am Math Soc RJ,1988.
[7] TEMAM R. Infinite-dimensional dynamical systems in mechanics and physics[M]. New York:Springer-Verlag,1988.
[8] FEIREISL E. Global attractors for semilinear damped wave equation with supercritical exponent[J]. J Diff Eqns,1995,116:431-447.
[9] SUN C Y, YANG M H, ZHONG C K. Global attractors for the wave equation with nonlinear damping[J]. J Diff Eqns,2006:427-443.
[10] SELL G R, YOU Y. Dynamics of Evolutionary Equations[M]. New York:Springer,2002.
[11] MA Q F, WANG S H, ZHONG C K. Necessary and sufficient conditions for the existence of global attractors for semigroups and applications[J]. Indiana University Math J,2002,51(6):1541-1559.
[12] 周蜀林. 偏微分方程[M]. 北京:北京大学出版社,2005.
[13] CHUESHOV l, LAIECKA I. Attractors for second-order evolution equations with a nonlinear damping[J]. J Dyn Diff Eqns,2004,16(2):469-511.
[14] 江泽坚,孙善利. 泛函分析[M]. 北京:高等教育出版社,1994.
[15] DAFERMOS M. Asymptotic stabiblity in linear viscoelasticity[M]. Arch Ration Mech Anal,1970,37:297-308.
2010MSC:35B41
(编辑陶志宁)
Existence of Global Attractor for Nonlinear Damped Wave Eequation with Nonlinear Memory
LI Jing,PU Zhilin
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)
Abstract:The paper aims to study the existence of global attractor for nonlinear damped wave equation with nonlinear memory. Based on the new priori estimate that proves semigroup possesses asymptotic compactness, the paper demonstrates that the attractor in such an equation with Dirichlet boundary condition exists in (Ω)× L2(Ω).
Key words:global attractor; nonlinear damped; nonlinear memory; priori estimate; wave equation
doi:10.3969/j.issn.1001-8395.2016.01.004
中图分类号:O213.2; O226
文献标志码:A
文章编号:1001-8395(2016)01-0020-06
*通信作者简介:蒲志林(1963—),男,教授,主要从事偏微分方程的研究,E-mail:puzhilin908@sina.com
基金项目:国家自然科学基金(71171138)和国家自然科学基金青年基金(71301111)
收稿日期:2014-08-30
