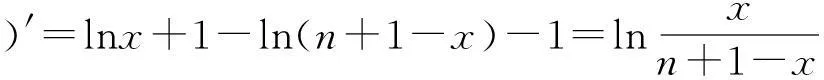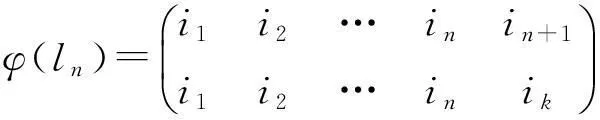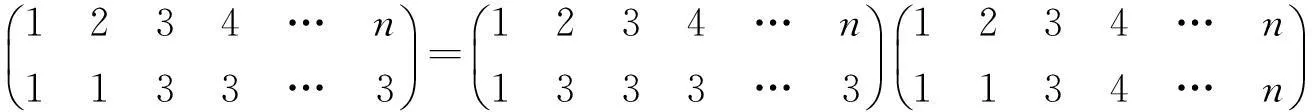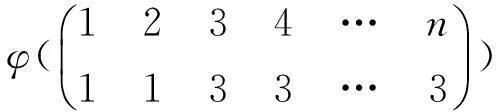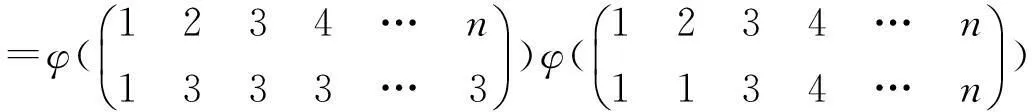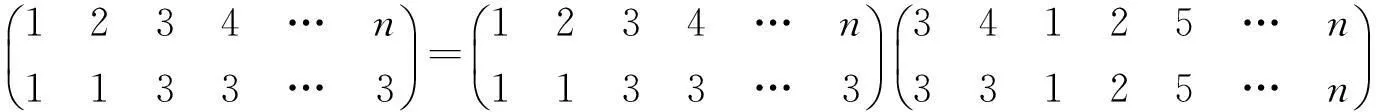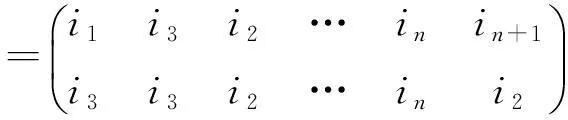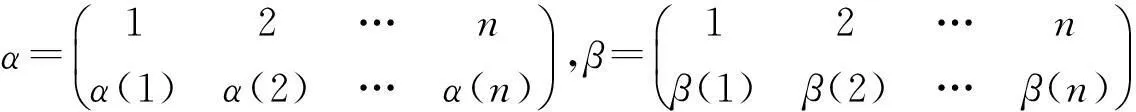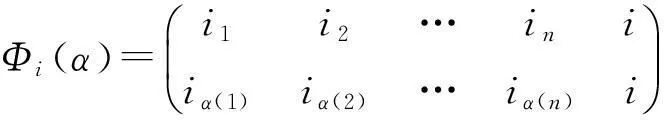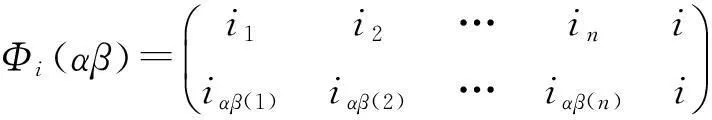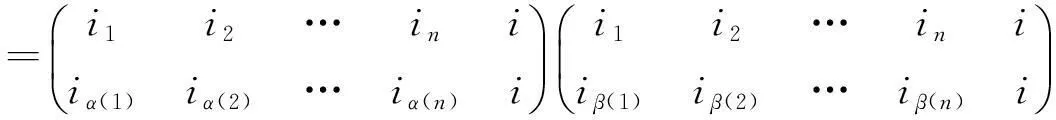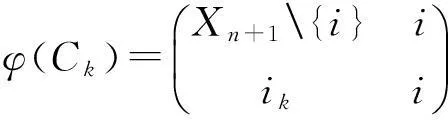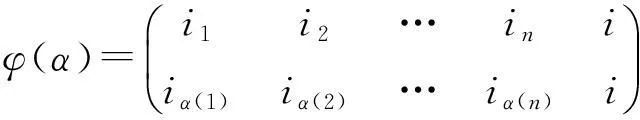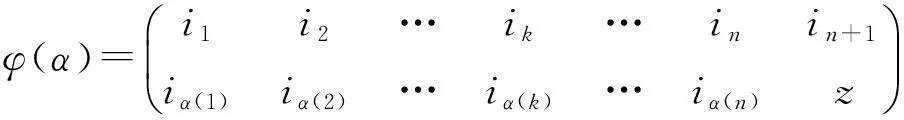两个全变换半群之间的同态II

唐 慧，杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

两个全变换半群之间的同态II

唐 慧，杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

令n为一个大于等于1的正整数,Tn和Tn+1分别是Xn={1,2,…,n}和Xn+1={1,2,…,n+1}上的全变换半群.本文在不考虑n=4的情况下刻画出Tn到Tn+1的所有同态.

全变换半群; 同态; 同余

1 引言和结论

设Tn是Xn上的全变换半群,在1998年Schein.B.M.和Teclezghi.B.[1]刻画出Tn的所有自同态,接下来我们自然去研究两个全变换半群Tn和Tm之间的同态.当n>m时的同态已经研究出来[2].在本文中将刻画出当m=n+1且不考虑n=4时Tn到Tm的所有同态.

(1)令ε为Tn+1中的一个幂等元.定义映射Φε:Tn→Tn+1为:对任意的α∈Tn,Φε(α)=ε.

(2)令ε,δ为Tn+1中两个不同的幂等元,且满足条件εδ=δε=δ.定义映射Ψε,δ:Tn→Tn+1如下:

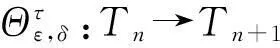
我们的主要结果如下

定理1 (i)取定i∈Xn+1,定义Φi为Tn到Tn+1的一个映射如下:首先规定

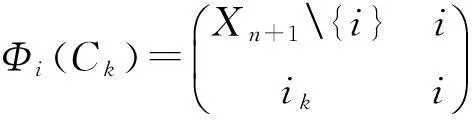
其中k∈Xn,{i1,i2,…,in}=Xn+1{i},然后任取α∈Tn{C1,…,Cn},规定

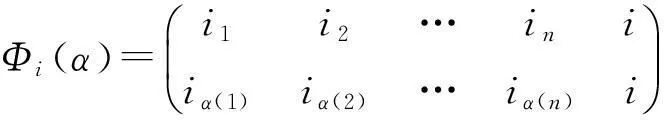
则Φi为Tn到Tn+1的一个单同态.

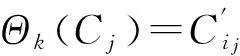
则Θk为Tn到Tn+1的一个单同态.

反之,Tn到Tn+1任一个单同态φ都具有形式(i)或者(ii).显然在除去n=4的情况下此结论也成立.

(iii)当φ为非单且n≠4时,则φ是同态当且仅当φ为如下形式之一:

(1)Φε,其中ε为Tn+1中的一个幂等元;

(2)Ψε,δ,其中ε,δ为Tn+1中两个不同的幂等元,且满足条件εδ=δε=δ;

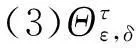
反之,当n≠4时,Tn到Tn+1的每个非单同态都具有形式(iii).

2 结论的证明

为叙述方便,令α∈Tn,记im(α)={α(x)|x∈Xn},rank(α)=|im(α)|,ker(α)={(x,y)∈Tn×Tn|α(x)=α(y)}.于是全变换半群Tn上的Green关系[3-4]如下:任取α,β∈Tn,有

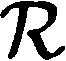
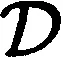
为证明我们的结论,需要引入如下几个引理.

令α,β∈Tn,且α,β有如下形式:

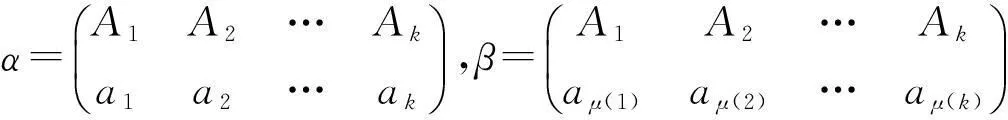
(1)

(1)若rank(α)

(2)若rank(α)>k,则α≡Rβ当且仅当α=β;

(2)令ρ是Tn上的任一个非泛同余,则存在k∈{1,2,…,n}与Sk的一个正规子群R,使得ρ=≡R.

引理2 设φ:Tn→Tn+1为同态,则对Tn中的任两个常值变换Ci和Cj有kerφ(Ci)=kerφ(Cj).

证明 任取(a,b)∈kerφ(Ci),则φ(Ci)(a)=φ(Ci)(b),因为CjCi=Cj,从而由φ为同态知

φ(Cj)(a)=φ(CjCi)(a)=φ(Cj)φ(Ci)(a)=φ(Cj)φ(Ci)(b)=φ(Cj)(b),

因此(a,b)∈kerφ(Cj),进而kerφ(Ci)⊆kerφ(Cj),同理可证得kerφ(Cj)⊆kerφ(Ci),故kerφ(Ci)=kerφ(Cj).

证明 对任意的x∈Ai,任意的α∈Tn,令φ(α)(x)=y,则由φ为同态知

φ(C1)(y)=φ(C1)φ(α)(x)=φ(C1α)(x)=φ(C1)(x),

引理4 设φ:Tn→Tn+1为单同态,若kerφ(C1)不是泛关系,则kerφ(C1)的等价类为{i}和Xn+1{i},其中i∈Xn+1.

证明 令kerφ(C1)的等价类分别为A1,A2,…,Ak,(k≥1),则由引理3知对任意的α∈Tn,任意的t∈{1,2,…,k},有φ(α):At→At.因此φ(Tn)⊆TA1×TA2×…TAK,其中TAj表示Aj上的全变换半群,令A1=x,则1≤x

nn=|φ(Tn)|≤|TA1|·|TA2|…|TAk|≤|TA1|·|TA2∪A3∪…∪Ak|

=xx·(n+1-x)n+1-x,

(2)

注意当x=1时式(2)等号成立.下证式(2)成立当且仅当x=1.

令f(x)=xx·(n+1-x)n+1-x,对此等式取对数得

lnf(x)=xlnx+(n+1-x)ln(n+1-x),

(3)

φ(α)(i1)=iα(1),φ(α)(i2)=iα(2),…,φ(α)(in)=iα(n).

证明 任取Cx∈Tn,x∈Xn,则有αCx=Cα(x),从而由φ为单同态知

因此有φ(α)(ix)=iα(x),x∈Xn,故φ(α)(i1)=iα(1),φ(α)(i2)=iα(2),…,φ(α)(in)=iα(n).

其中k∈{1,2,…,n}.

进而当n≥4时,由

和引理5有

(4)

另一方面,由

和引理5又有

(5)

(4)与(5)矛盾,故y=i1不成立.

(6)

(7)

(6)与(7)矛盾,故y=i3不成立.

综上所述,x≠in+1,从而x=ik,其中k∈{1,2,…,n}.

定理1的证明 易证定理1中(iii)的映射都为Tn到Tn+1的同态.下面验证Φi和Θk都是Tn到Tn+1的单同态.

任取α∈Tn,β∈Tn,且

从而

则由Φi的定义知

其中{i1,i2,…,in}=Xn+1{i},从而

因此Φi(α)Φi(β)=Φi(αβ),所以Φi是Tn到Tn+1的一个同态,又令Φi(α)=Φi(β),从而α(x)=β(x),其中x∈Xn,进而Φi是单的,故Φi是Tn到Tn+1的一个单同态.同理可证Θk是Tn到Tn+1的一个单同态.

现令φ为Tn到Tn+1的任一个同态,由于ker(φ)为Tn上的一个同余,于是据引理1,分两种情况如下:

情况1 ker(φ)是泛同余,则φ把Tn映到Tn+1中的某个幂等元,令这个幂等元为ε,从而φ为常量同态,且φ为定理1中的形式(iii)中的(1);

情况2 ker(φ)是非泛同余,则ker(φ)=≡R,R◁Sk.根据k

情况2.1 若k

因此有φ(α)(i1)=iα(1),φ(α)(i2)=iα(2),…,φ(α)(in)=iα(n),φ(α)(i)=i,进而

其中{i1,i2,…,in}=Xn+1{i},故φ具有形式(i).

情况2.1.2φ:Tn→Tn+1为单同态,kerφ(C1)为泛关系.据引理6有k∈Xn,使得

其中{i1,i2,…,in+1}=Xn+1.于是对任意的α∈Tn,由引理5可设

又αln=α,从而由φ为同态知φ(αln)=φ(α)φ(ln)=φ(α),就推出z=iα(k),故φ具有形式(ii).

[1] SCHEIN B M, TECLEZGHI B. Endomorphisms of Finite Full Transformation Semigroups [J]. Proceedings of The American Mathematical Society, 1998, 126(9):2579-2587.

[2] 唐慧,杨秀良.两个全变换半群之间的同态I[J].杭州师范大学学报(自然科学版),2015,14(5):527-530.

[3] GANYUSHKIN O, Mazorchuk V. Introduction to Classical Finite Transformation Semigroups [M]. London: Springer Verlag,2009.

[4] DOSS C. Certain equivalence relation in transformation semigroups[D]. Nashville: Univ of Tennessee, 1955.

[5] MAL’SEV A. Symmetric groupoids [J]. Mat Sbornik,1952,73(1):136-152.

Homomorphisms of Two Full Transformation Semigroups II

TANG Hui, YANG Xiuliang

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

Letnbe the positive integer which is greater than or equal to 1,TnandTn+1are the full transformation semigroup on finite setXn={1,2,…,n} andXn+1={1,2,…,n+1} respectively. This paper describes all homomorphisms fromTntoTn+1while does not considern=4.

full transformation semigroup; homomorphism; congruences

2015-06-27

杨秀良(1963—)，男，教授，主要从事半群代数研究.E-mail: yxl@hznu.edu.cn

10.3969/j.issn.1674-232X.2016.02.011

O152.7 MSC2010:43A22

A

1674-232X(2016)02-0178-06