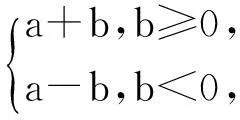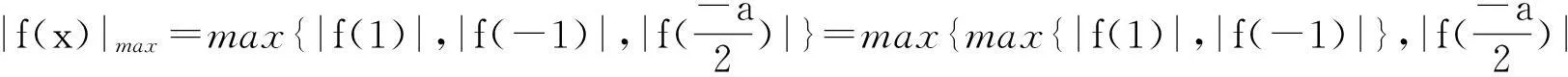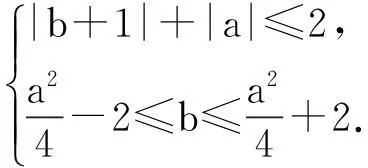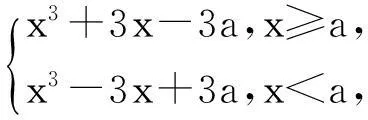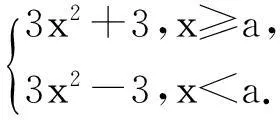双参数恒成立不等式中含参函数的最值问题初探——兼谈“函数最值难确定”时的变通策略



双参数恒成立不等式中含参函数的最值问题初探
——兼谈“函数最值难确定”时的变通策略

浙江省衢州第二中学(324000 )傅建红

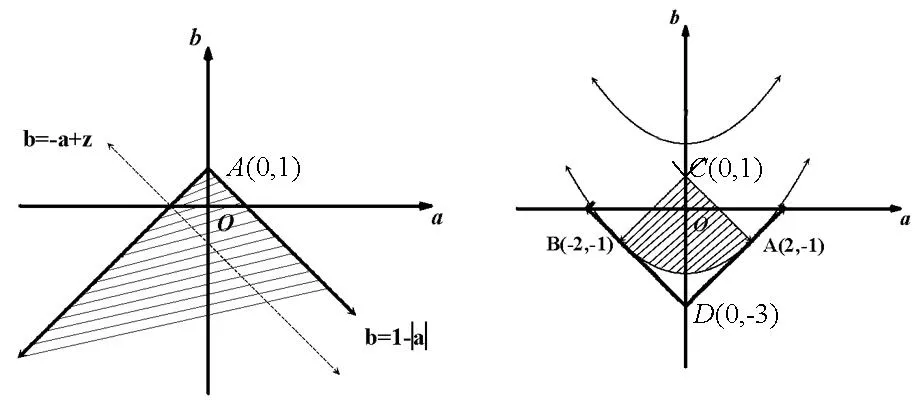
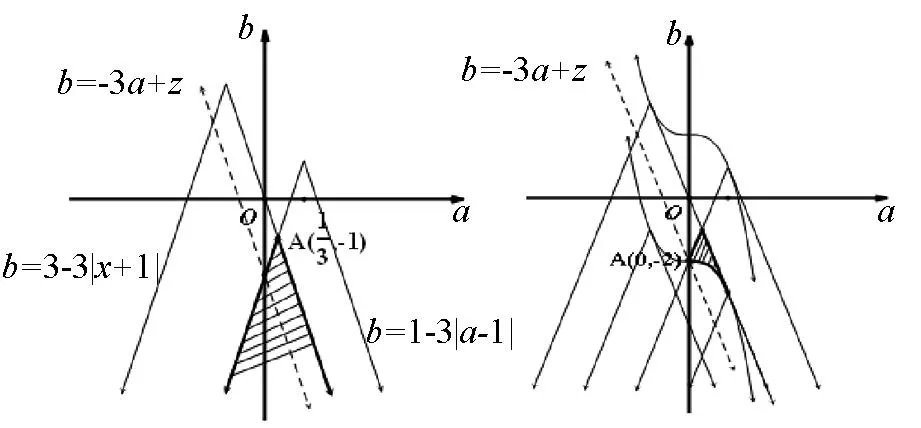
在高三复习中，笔者常常遇到类似如下的两类恒成立不等式问题：(1)“若不等式f(x,a)≤0对一切x∈[m,n](m

一、预备性质

性质1已知a,b∈R，(1)max{a+b,a-b}=a+|b|；(2)min{a+b,a-b}=a-|b|.

证明：(1)因为max{a+b,a-b}=

性质2已知a,b∈R，(1)max{|a+b|,|a-b|}=|a|+|b|；(2)min{|a+b|,|a-b|}=||a|-|b||.

性质3(1)“V型”函数(左减右增)在闭区间内的最大值仅在区间端点处取得；(2)“W型”函数(减增交替2次)在闭区间内的最大值在区间端点或极大值点处取得.

说明：“V型”、“W型”仅示意函数f(x)在其自然定义域D上的大致形状，而函数在其实际定义区间[m,n](n>m)([m,n]⊆D)上的形状可能不再是“V型”、“W型”.事实上，“V型”函数在闭区间[m,n](m

max{max{f(m),f(n)},f(x0)}(其中x0是f(x)的极大值点).换言之，由于在闭区间[m,n](m

性质4已知xi,r∈R(i=1,2,…,n)，(1)max{x1,x2,…,xn}≤r⟺xi≤r(i=1,2,…,n)；(2)min{x1,x2,…,xn}≥r⟺xi≥r(i=1,2,…,n).

说明:性质3、4的正确性都是显而易见的，证明从略.

二、举例说明

例1(2015年·浙江(理)改编) 已知函数f(x)=x2+ax+b(a,b∈R).

(1)若f(x)≤2对x∈[-1,1]恒成立，求a+b的最大值；

(2)若|f(x)|≤2对x∈[-1,1]恒成立，求|a|+|b|的最大值.

解：(1) 由题意，f(x)max≤2(x∈[-1,1]).易知f(x)为“V型”函数，所以f(x)在[-1,1]上的最大值f(x)max=max{f(1),f(-1)}.因为f(1)=(1+b)+a，f(-1)=(1+b)-a，故由性质1得，f(x)max=1+b+|a|，所以题意即为b≤1-|a|.在直角坐标系aOb下，画出不等式b≤1-|a|对应动点(a,b)的可行域(如图1).设z=a+b，它对应的直线为l，易知z的几何意义为l在b轴上的截距.观察图像可知，当l平移至与阴影的右边界重合时(A(0,1)为其中一个最优解)，z取得最大，即zmax=0+1=1.

图1 图2

例2(2014年浙江(理)改编)已知a,b∈R，函数f(x)=x3+3|x-a|.

(1)若f(x)+b≤2对x∈[-1,1]恒成立，求3a+b的最大值；

(2)若|f(x)+b|≤2对x∈[-1,1]恒成立，求3a+b的最小值.

解：(1)由题意f(x)=

图3 图4

(2)易知当a≤-1及a≥1时，|f(x)+b|为“单调型”或“V”函数，而当-1

|f(x)+b|max=max{|f(1)+b|,|f(-1)+b|,|f(a)+b|}.∵|f(1)+b|=|1+3|a-1|+b|，|f(-1)+b|=|-1+3|a+1|+b|，|f(a)|

+b=|a3+b|，故由题意结合性质4得，|1+3|a-1|+b|≤2、|-1+3|a+1|+b|≤2、|a3+b|≤2.在直角坐标系aOb下，分别画出不等式b≥-3|a-1|-3、b≤-3|a-1|+1、b≥-3|a+1|-1、b≤-3|a+1|+3、b≥-a3-2、b≤-a3+2对应动点(a,b)的可行域(如图4).设z=3a+b，它所对应的直线为l，易知z的几何意义为直线l在b轴上的截距，观察图中阴影易知，当l平移至点A(0,-2)时，z取得最小，即zmin=3×0+(-2)=-2.

点评：上述两题的解法如出一辙：(1)首先判断函数在其自然定义域内是“单调型”、“V型”还是“W型”，以便由性质3了解函数在其实际定义区间内的最值可能出现在哪几个之中，然后利用性质4对区间端点和极值点进行“整体控制”；(2)在平面直角坐标系aOb下，画出“整体控制”下所得不等式(显然它们是关于变量a,b的约束条件)中动点(a,b)的可行域，然后利用线性规划，求出目标函数z=h(a,b)的最值(此解法对曲线作图的要求较高).不难看出，利用性质可以回避繁琐、细碎的分类讨论，使问题的解决更直接、更快捷；利用线性规划可使问题自然直观、一目了然，从而体验此类问题中“与众不同”的数形结合.

综上可知，当含参恒成立不等式遭遇“函数最值难确定”的挑战时，我们可以不必正面强求，而是顺其自然、“避实就虚”，通过对“可能最值”的“整体控制”，从而使问题变通解决.但“整体控制”之后仍有很长的路要走，此时“曲线作图”和“线性规划”就犹如一套“组合拳”，它们在通往参数函数最值的途中功不可没.

参考文献

[1]章丽.也谈含参不等式恒成立问题的解法探究[J].中学数学,2014，(2)：83-84.