2015年高考北京卷第19题的本质探究



2015年高考北京卷第19题的本质探究

北京市陈经纶中学(100020)张留杰

题目(2015年高考数学北京卷(理科)19)

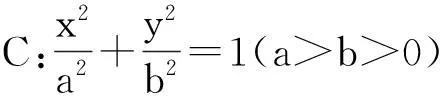
(1)求椭圆C的方程，并求点M的坐标(用m，n表示)；

(2)设O为原点，点B与点A关于x轴对称，直线PB交x轴于点N．问：y轴上是否存在点Q，使得∠OQM=∠ONQ？若存在，求点Q的坐标；若不存在，说明理由．

一、试题的分析与解答

本题从题目本身看属于探究型问题，并且和角度有关，立意新颖．从解决问题的层面来看，虽然考查了直线与椭圆的位置关系，但是打破了“联立—消元—根与系数的关系等”定势思维．突出考查了图形中“位置关系”如何向“数量关系”的转化，考查了椭圆的对称性．

(2)假设存在y轴上点Q(0,t)，使得∠OQM=∠ONQ，如图1．

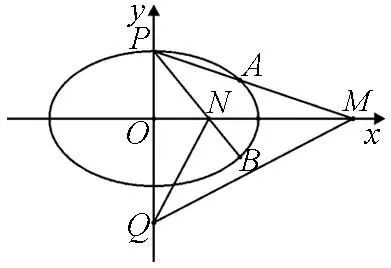
图1

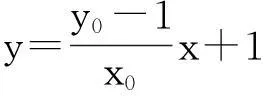
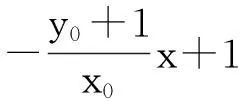
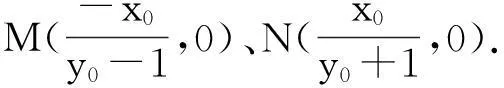
二、试题的本质探究

波利亚的《怎样解题》中提出“回顾与反思”也许会有新的发现和感受．回顾上述解题过程，发现|OM|·|ON|的值恰好为椭圆中的a2，是巧合还是必然？发现点Q满足△QON和△MOQ相似，由于椭圆可以看做由圆压缩变换而来，于是思考：该问题在圆中是否有更本质的几何解释呢？笔者带着这些问题做了如下探究．

探究1如图2，圆O的半径为R，PQ和CD是两条互相垂直的直径，点A在圆O上，且点A关于直径CD的对称点为B，直线PA交直线CD于点M，PB交CD于N，则OM·ON=R2．

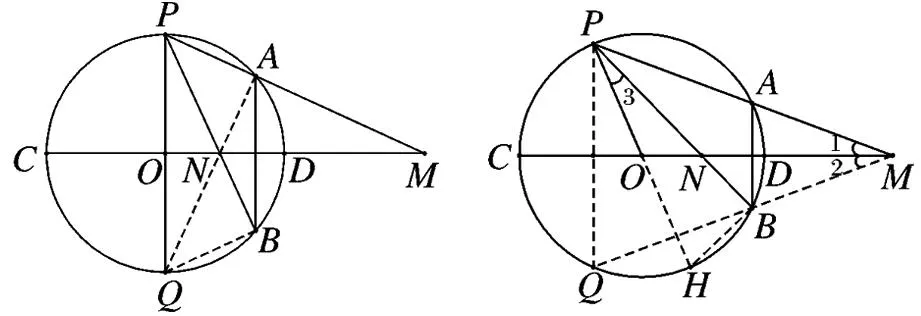
图2 图3

简证：依题意，易得四边形APQB为等腰梯形，PA⊥AQ，AB⊥CD，所以 ∠QPB=∠QAB=∠AMN，即∠OPN=∠OMP，所以Rt△OPN∽Rt△OMP，所以OP2=OM·ON=R2，证毕．

根据圆的对称性及OM·ON的值，发现结论和点P在圆上的位置无关．于是得出:

探究2如图3，圆O的半径为R，CD为一条直径，点P、A在圆O上，点A关于直径CD的对称点为B，直线PA交直线CD于点M，PB交CD于N，则OM·ON=R2．

简证：如图3，作点P关于直径CD的对称点Q，连PO并延长交圆于H，连结BH，根据圆的对称性，易得Q、B、M三点共线，且∠1=∠2．因为∠Q=∠H，∠Q+∠2=90°，∠H+∠3=90°，所以∠3=∠2，所以∠3=∠1，∠PON=∠MOP，所以△PON∽△MOP，所以得OP2=OM·ON=R2，证毕．

三、试题的一般性及推广

根据探究2，大胆猜想在椭圆中结论|OM|·|ON|=a2也与点P的位置无关，于是有如下的一般性结论．

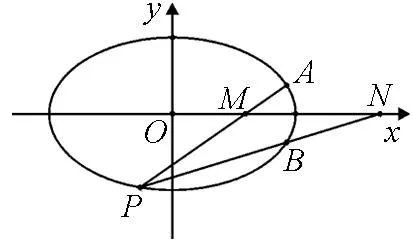
图4

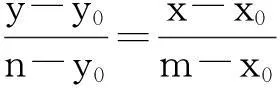
根据椭圆的对称性可知，如果结论1中的点A与点B关于y轴对称，还不难得出：

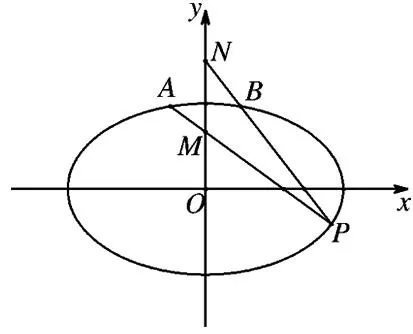
图5

由于双曲线和椭圆都是有心圆锥曲线，能否将这些结论推广到双曲线呢？经过进一步探究得出：

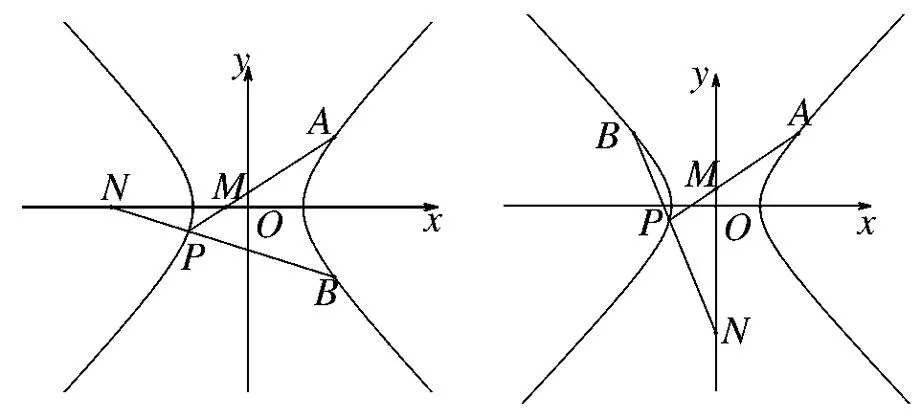
图6

(证明过程可参考结论1，这里从略)

通过探究与推广，得出了这道高考试题背后蕴藏的一般性结论，揭示了该问题所体现的椭圆性质的本质，深感高考试题的内涵丰富！