可渗透岛礁环境下的波浪运动研究

王 科，陈彧超，施鹏飞，边 疆

（大连理工大学 工业装备与结构分析国家重点实验室，工程力学系，辽宁 大连 116024）

可渗透岛礁环境下的波浪运动研究

王 科，陈彧超，施鹏飞，边 疆

（大连理工大学 工业装备与结构分析国家重点实验室，工程力学系，辽宁 大连 116024）

文章应用边界单元法，依据波浪绕射理论研究了潜淹没岛礁上的波浪运动问题。研究中分析了岛礁的渗透性、排布的数量、环礁泻湖的深度等因素对于岛礁消波作用的影响，获得了不同岛礁环境下波浪的透射系数、反射系数。研究发现，可渗透岛礁的消波效果比不可渗透岛礁差，且孔隙率越大，岛礁对于波浪的消波效果越小；单个岛礁对长波有明显的消波作用，而对中短波几乎没有影响；但随着岛礁排布数量的增加，岛礁群对于中波的消波效果增加；环礁的消波效果受到泻湖深度的影响，在一定范围内，泻湖的深度越大，环礁对于中短波的消波效果越好，但当泻湖深度达到一定数值后，继续增大深度，消波效果基本没有提高。

可渗透岛礁；边界单元法；波浪透射及反射系数；泻湖

0 引 言

我国的海域面积超过400万平方公里，南海地区有许多宽度达数公里、且潜深较小的珊瑚礁，这些自然岛礁与潜式防波堤类似，有一定的消波能力。对于这些岛礁，在开发其渔业及旅游价值的同时，还可以充分利用其消波和护岛功能，在周边设置浮式结构物，甚至构建机场、补给基地等大型设施，来辅助矿产开采、渔业生产、科研观测等海洋开发活动[1]。要实现这些构想，对于岛礁环境下的波浪运动研究显得非常重要。

早期主要通过监测及试验手段来研究岛礁环境下的波浪运动问题，Hardy等人[2]在1990年对澳大利亚大堡礁进行可观测试验来研究珊瑚礁与波浪的相互作用，结果表明岛礁的消波作用很大程度上受其礁顶深度的影响。Gourlay（1994）[3]，用模型实验研究了岛礁环境下不同波浪条件和不同水深条件下的波浪透射特性。Lowe等人（2005）[4]在夏威夷卡内奥赫湾的堡礁开展了两星期的实验，布置多个测点来监测波高、波速，研究了岛礁对于波浪的消波作用。

近年来，考虑到岛礁有着与潜式防波堤类似的特点，一些水动力计算方法开始被用于岛礁波浪的相互作用研究。Hearn等人（1999）[5]引入了深度系数，用一维模型研究了岛礁及泻湖的水动力特性，分析了深度系数对岛礁水动力特性的影响，并用澳大利亚宁格罗暗礁（Ningaloo reef）和美国卡内奥赫湾（Kaneohe Bay）的相关数据检验了模型的准确性。丁军等人（2014）[6]，用Morison公式和Green函数法研究了岛礁环境下半潜式平台的运动响应。田超等人（2014）[7-8]通过模型实验，研究了岛礁环境下波浪变形及浮式结构的运动响应，并通过缓坡方程引入了半潜式平台在岛礁环境下的岛礁影响系数，提出了一种岛礁环境下浮式结构运动响应的预报方法。Fang等人（2014）[9]用Boussinesq波浪模型并考虑波浪破碎及底部摩擦因素，对不同波浪条件及岛礁环境下的波浪运动特性进行了数值模拟，结果与监测数据吻合较好。

本文依据波浪绕射理论，发展了能求解任意复杂边界的边界元算法。通过算例验证，证明了本文采用的边界元算法对于潜淹没结构上波浪运动问题的精确性，并对潜淹没岛礁上的波浪运动问题进行了研究。本文计算了不同岛礁环境下波浪的透射系数、反射系数，分析了岛礁的渗透性、排布的数量、环礁泻湖的深度这几个因素对于岛礁消波作用的影响。

1 数学理论及基本计算公式

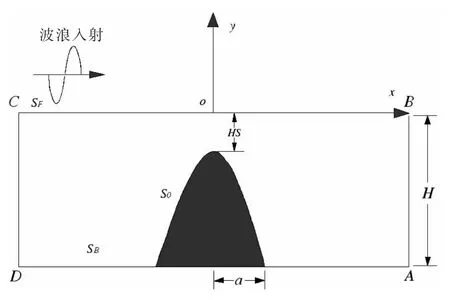
图1 计算示意图Fig.1 Calculation sketch

1.1 边界值问题基本公式

如图1所示，一个抛物线形的岛礁位于水底，水深H，岛礁宽度为B=2a，其顶部距水面距离为HS。建立如图所示的笛卡尔坐标系，取原点o位于水面，波浪沿着x轴正方向入射。考虑不可压缩、无粘性理想流体，则流速可以用速度势函数的梯度表示，流体速度势可以表示为：

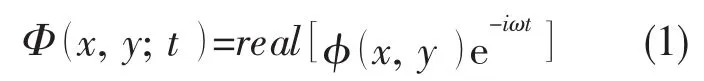
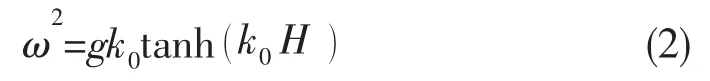
在自由表面SF上，速度势满足线性自由表面条件：

若水底为不可渗透边界，则在水底满足：

若物面S0可渗透，则可将流场分成两个区域：外流域Φ1和可渗透结构内流域Φ2，两个流域的速度势都满足拉普拉斯方程。考虑到相邻流域必须在交界面上满足连续性方程，则速度势函数满足：

其中：ε表示可渗透结构的孔隙率，S为惯性系数，f为线性阻尼系数（Sollitt and Cross,1972），f可以通过下列公式求得[10]：

其中：ν为运动粘度，Cf为湍流阻力系数，KP为渗透介质的固有渗透系数，q表示渗流速度的实部。Cf和KP是渗透介质的本身特性，需要由实验测得，f则需要迭代求解得到。

计算边界离岛礁足够远时（大于5倍水深），可认为反射和透射波浪达到定常状态，速度势满足：

基于线性假设，可以将速度势分解为入射势φI与绕射势φD：

其中：φI为微幅波入射势，可表示为：

其中：A为入射波振幅。

1.2 边界积分方程

对于波浪绕射问题，根据格林定理得到如下边界积分方程：

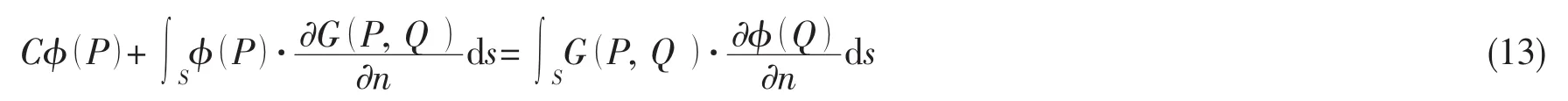
如取格林函数基本解为下式，则可采用镜像方法消除水底边界积分：

当物面边界不可渗透时，将边界条件（4）、（5）、（6）和（10)代入（15）式，得到：

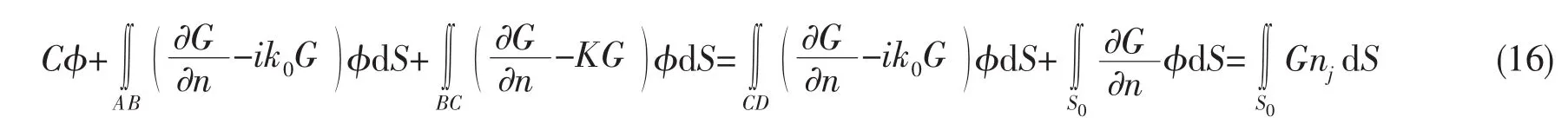
1.3 透射系数与反射系数

透、反射系数可以计算如下，定义：

其中：eHR，eHI分别为eH的实部和虚部，相位α1为：

类似地，定义：

其中：eSR，eSI分别为eS的实部和虚部，相位α2为：

反射系数RF和透射系数RT可表示为：

1.4 可渗透岛礁波浪运动研究

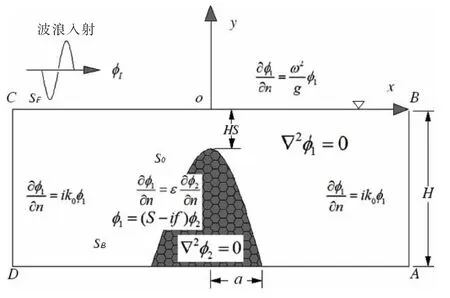
图2 可渗透结构计算示意图Fig.2 Sketch of permeable structure

对于物面边界不可渗透的情况，只存在一个流域，只需对外域的积分方程进行求解，计算速度势。而当物面边界为可渗透边界时，流场分为外部流域和渗透结构的内部流域，见图2，物面边界条件变为内外速度势φ1，φ2及其导数的相互关系，此时需对内外流域进行迭代求解，来计算内外速度势。

一般采用如下迭代步骤：

（5）具体程序执行框图见图3。

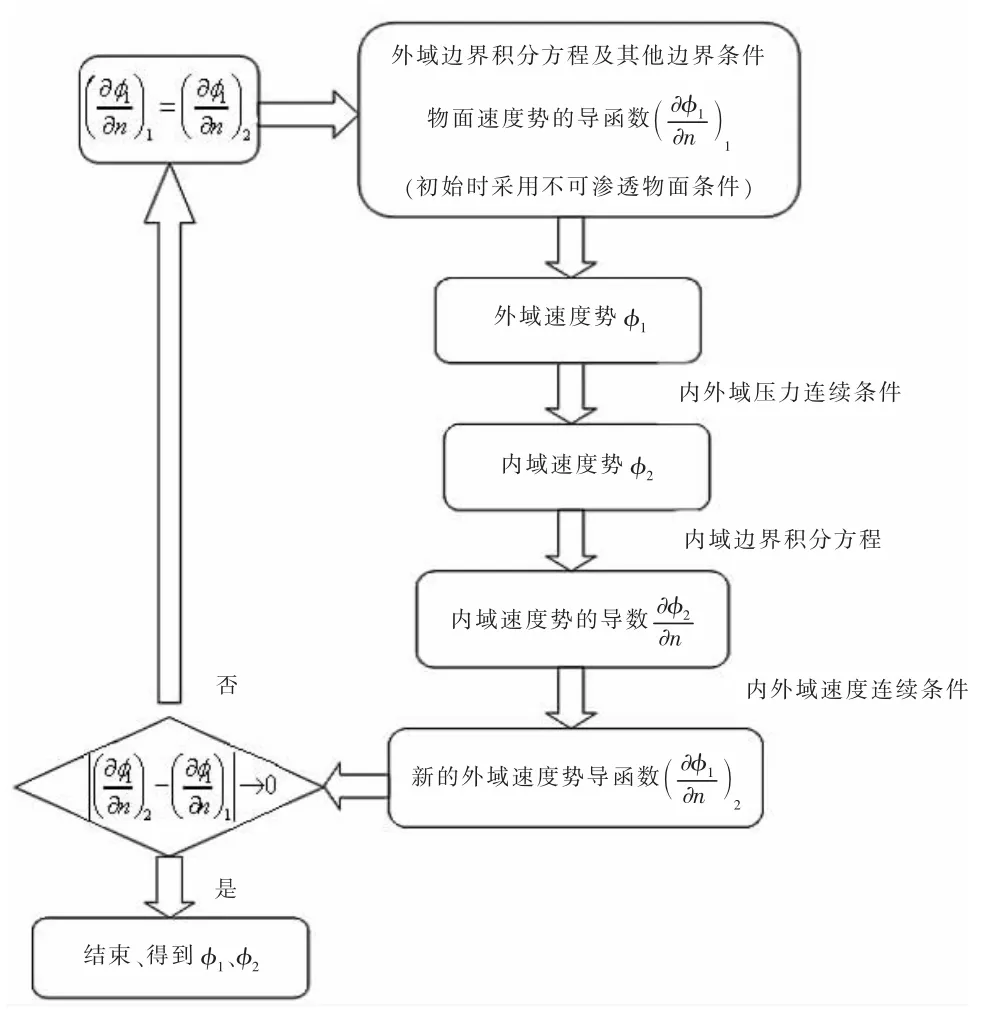
图3 迭代计算示意图Fig.3 Sketch of iterative computation

2 结果与分析

2.1 算例验证

为了验证本文采用边界元算法的精确性，本文对潜淹没矩形防波堤的波浪运动问题进行了研究，计算了其反射系数，并将结果与Cho和Lee（2004）[11]的实验数据进行了比较。如图4所示，考虑一组不可渗透的矩形结构，在水下依次排布，其尺寸为宽度la=高度lb=0.4 m，潜深Hs=0.4 m，矩形结构的间距d为2.0 m，水深H为0.8 m，波高h为0.04 m。

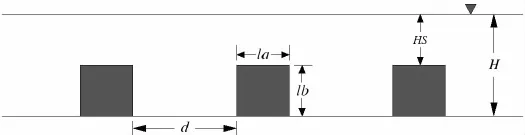
图4 潜没式矩形防波堤的示意图Fig.4 Sketch of submerged rectangular breakwater

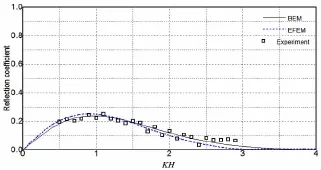
图5 N=1时反射系数计算结果比较Fig.5 Comparison of reflection coefficient when N=1

Cho和Lee（2004）[11]对此问题进行了实验研究，分别测得矩形个数N=1～3情况下的反射系数，并与特征函数展开法的计算结果进行了比较。本文通过边界元方法对此算例进行计算，对于每个潜淹没矩形结构划分180个边界单元，得到反射系数结果如图5～7所示，图中横坐标为无因次化波数KH。可以看到，边界元法的计算结果与Cho和Lee（2004）[11]的实验数据吻合较好，与特征函数展开法的结果接近但也存在一定差异：边界元法的结果曲线在前半段略小于特征函数展开法，而在后半段则略大于特征函数展开法，但是总体上两者的计算结果比较接近。这说明对于波浪与结构物相互作用的问题，边界元方法有较高的计算精度。

2.2 岛礁的渗透性对于波浪运动的影响分析

对于岛礁计算模型，经反复试算，将图2中流域边界沿水平方向划分成840个边界单元，垂直方向划分140个边界单元，将每个岛礁边界划分为180个边界单元进行计算。可渗透岛礁潜没于水面下，物面边界S0为可渗透边界，计算中具体取值如下：单个岛礁宽度B=2a=2.0 m，水深H=4.0 m，潜深HS=0.5 m，取湍流阻力系数Cf=0.295，固有渗透系数KP=1.057 2×10-7m2（Hsu和Wu，1999）[12]，运动粘度ν=1.0126×10-6m2/s[13]。取平均孔隙率ε分别为0.1，0.2，0.3，0.4，0.5。下图中横坐标为无因次化波数Ka，入射波浪振幅均为单位值。

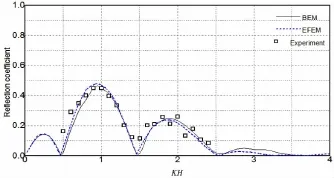
图6 N=2时反射系数计算结果比较Fig.6 Comparison of reflection coefficient when N=2

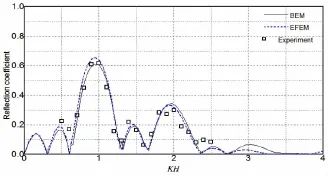
图7 N=3时反射系数计算结果比较Fig.7 Comparison of reflection coefficient when N=3

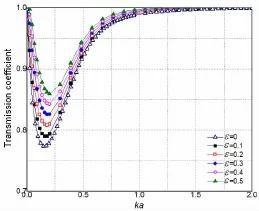
图8 可渗透岛礁的透射系数Fig.8 Transmission coefficient of a permeable reef with different porosity

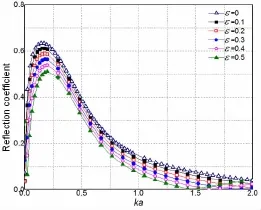
图9 可渗透岛礁的反射系数Fig.9 Reflection coefficient of a permeable reef with different porosity

图8～9中ε=0的透、反射系数曲线为不可渗透岛礁的计算结果。可以看到，渗透性并不影响曲线随着相对波数Ka的增减变化趋势，以及峰值出现的相应位置；但随着平均孔隙率ε的增大，反射系数逐渐减小，透射系数逐渐增大。当岛礁不可渗透时，反射系数在Ka=0.17处达到最大值，此时反射系数为0.63；而当孔隙率ε达到0.5时，反射系数的最大值仅为0.50。

根据王新志等人（2008）[14]的实验结果，我国南沙群岛的礁灰岩孔隙率为45%～55%；本文的计算结果显示，ε=0.5时的反射系数峰值约为不可渗透情况下80% ，可见，礁灰岩岛礁的防浪作用要明显差于不可渗透岛礁。

2.3 岛礁排布数量对于波浪运动的影响

考虑一组不可渗透的岛礁，在水下连续排布，单个岛礁宽度仍然取为B=2a=2.0 m，水深为H=4.0 m，潜深HS=1.0 m，取岛礁间距d=B=2.0 m，计算岛礁排布数量N分别为1，2，3时的相关参数，图10为多岛礁的计算示意图，计算结果如图11～12所示。

单个岛礁的透、反射系数曲线呈抛物线状，反射曲线的最大值约为0.45，透射曲线的最小值约为0.9；当N=2时，透、反射系数曲线出现两处峰值：在Ka=0.05处，反射系数约为0.45，透射系数为0.89，在Ka=0.45处，反射系数达到0.5，透射系数减小到0.86；当N=3时，结果曲线的变化更为剧烈，有3处比较明显的波峰：在Ka=0.02和Ka=0.2处，透射、反射系数达到峰值，反射系数为0.45，透射系数为0.9，在Ka=0.55处，反射系数达到最大值，约为0.62，透射系数则减小为0.78。

随着岛礁排布数量N的增大，透射、反射系数曲线的变化愈发剧烈。以反射系数为例，随着N的增大，出现了更多的波峰。双岛礁情况下产生的第一个波峰，和三个岛礁情况下产生的前两个波峰，其峰值和单个岛礁情况下的最大值基本相同，约为0.45，且都出现在0＜Ka＜0.3的长波范围内，这表明岛礁数量的增加不影响岛礁对于长波的作用，其对于长波的消波效果和单个岛礁基本相同；而在0.3＜Ka＜0.8的中波范围内产生的波峰，其峰值明显大于其他波峰，且随着岛礁数量的增加而增大：N=2时反射系数为0.5，N=3时，反射系数达到0.62，这表明岛礁数量的增加能加强岛礁对中波的消波作用。当Ka＞0.8时，不同岛礁对波浪的反射系数在0.2以下。

图10 多岛礁的计算示意图Fig.10 Sketch of multiple reefs

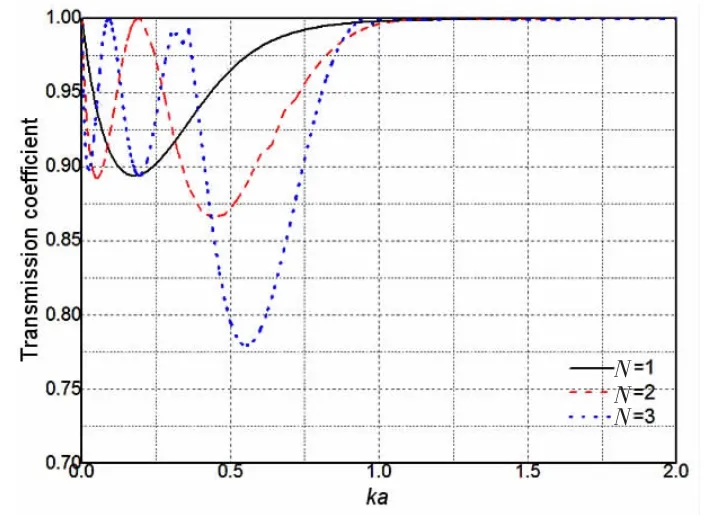
图11 不同数量岛礁的透射系数Fig.11 Wave transmission coefficients of multiple reefs

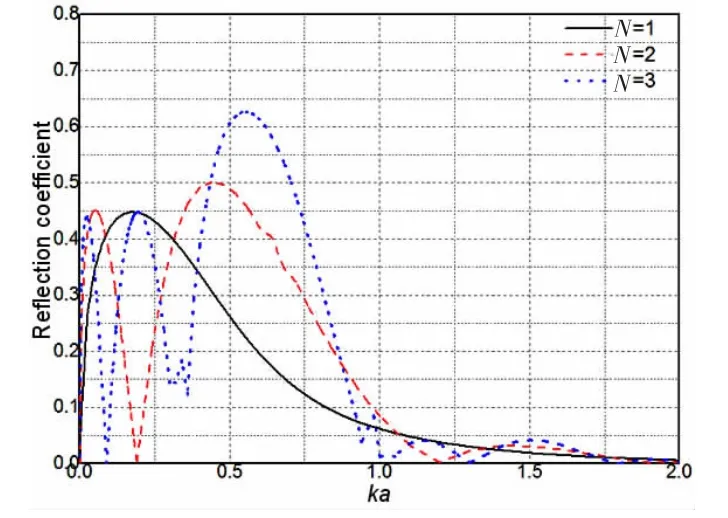
图12 不同数量岛礁的反射系数Fig.12 Wave reflection coefficients of multiple reefs

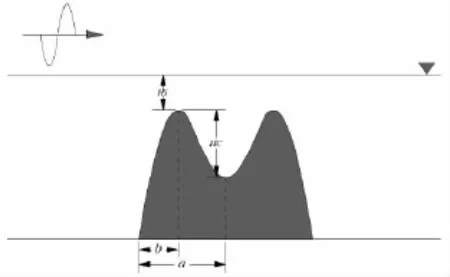
图13 环礁的计算示意图Fig.13 Schematic sketch of lagoon reef

综上所述，当潜深较大时，单个岛礁仅对长波有一定的消波作用，但是对中短波几乎没有效果；岛礁排布数量的增加，并不会改善岛礁对于长波的效果，但能够显著增强对于中波的阻碍作用。

2.4 环礁的波浪运动分析

我国南海的地区有许多环礁，例如华光礁、美济礁、仙娥礁等。珊瑚虫围绕岛屿繁殖形成环状珊瑚，当发生地质变化，岛屿下沉至海面以下，就形成了环礁及围绕其中的泻湖。

环礁的计算模型如图13所示，环礁潜淹没于水面以下，水深H=4.0 m，岛礁宽度B=2a=4.0 m，泻湖宽度为b=2.0 m，礁顶潜深HS=0.5 m，分别取泻湖相对礁顶的深度HC为0.5 m，1.0 m，1.5 m，2.0 m，2.5 m和3.0 m，计算其透射系数和反射系数。

从图14～15可以看到和双岛礁排布的情况类似，环礁的透射系数和反射系数随着相对宽度Ka的变化出现两个明显的波峰：第一个波峰出现在Ka=0.1处，第二个波峰出现在Ka=1.2处。以反射系数为例，泻湖相对礁顶的深度HC变化对第一个波峰的峰值影响很小，随着HC增大，第一个波峰的峰值几乎不变，约为0.65。HC由0.5增大到1.5的过程中，第二个波峰的峰值开始增大：HC=0.5时，为0.47，HC=1.0时为0.51，HC=1.5时，为0.52，而当HC达到1.5后，泻湖深度继续增大对反射系数的影响很小，这时环礁的消波作用不再随深度变大而增强。

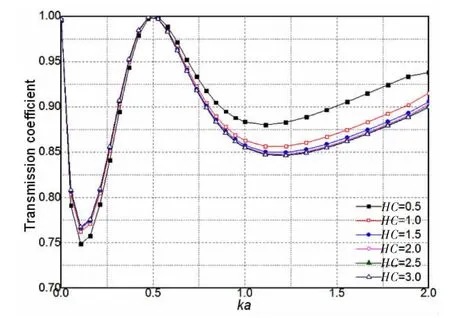
图14 泻湖深度不同时环礁的透射系数Fig.14 Transmission coefficient of lagoon reef with different lagoon depth

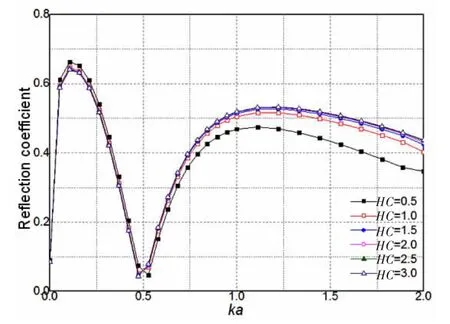
图15 泻湖深度不同时环礁的反射系数Fig.15 Reflection coefficient of lagoon reef with different lagoon depth

3 结 论

本文根据波浪绕射理论，应用边界元方法，对于岛礁环境下的波浪运动进行了计算，分析了岛礁渗透性，排布数量，环礁泻湖的潜深等因素对于波浪运动的影响，得到以下结果：

（1）可渗透岛礁的消波效果差于不可渗透岛礁，且孔隙率越大，岛礁对于波浪的阻碍越小。

（2）单个岛礁的消波作用集中在长波，而对中短波几乎没有效果；岛礁排布数量的增加，会增强岛礁对于中波的阻碍作用。

（3）环礁的消波效果受到其泻湖深度的影响，在一定范围内，泻湖深度越大，环礁对于中短波的消波效果越好；但当深度达到一定程度后，继续增大，则基本不影响其消波效果。

[1]吴有生,田 超,宗 智,等.波浪环境下超大型浮式结构物的水弹性响应研究[C].第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集（上册）,2013.

[2]Hardy T A,Young I R,Nelson R C,et al.Wave attenuation on an offshore coral reef[J].Coastal Engineering Proceedings, 1990,1(22):330-344.

[3]Gourlay M R.Wave transformation on a coral reef[J].Coastal Engineering,1994,23(1):17-42.

[4]Fernandes L,Day J O N,Lewis A,et al.Establishing representative no-take areas in the great barrier reef:Large-scale implementation of theory on marine protected areas[J].Conservation Biology,2005,19(6):1733-1744.

[5]Hearn C J.Wave-breaking hydrodynamics within coral reef systems and the effect of changing relative sea level[J].Journal of Geophysical Research:Oceans,1999,104(C12):30007-30019.

[6]丁 军,田 超,张 凯,等.近岛礁半潜式平台的运动及载荷响应研究[C].第十三届全国水动力学学术会议暨第二十六届全国水动力学研讨会论文集—F船舶与海洋工程流体力学,2014.

[7]田 超,丁 军,吴有生.近岛礁浮式平台水动力模型试验研究[C].第十三届全国水动力学学术会议暨第二十六届全国水动力学研讨会论文集—D水动力学实验和测试技术,2014.

[8]田 超,丁 军,杨 鹏.岛礁波浪环境下浮式结构物的动响应预报[J].船舶力学,2014,18(11):1284-1291. Tian Chao,Ding Jun,Yang Peng.Prediction of dynamic responses of floating structures under wave environment near islands and reefs[J].Journal of Ship Mechanics,2014,18(11):1284-1291.

[9]Fang K,Yin J,Liu Z,et al.Revisiting study on Boussinesq modeling of wave transformation over various reef profiles[J]. Water Science and Engineering,2014,7(3):306-318.

[10]Sollitt C K,Cross R H.Wave transmission through permeable breakwaters[J].Coastal Engineering Proceedings,1972,1(13): 1827-1846.

[11]Cho Y,Lee J,Kim Y.Experimental study of strong reflection of regular water waves over submerged breakwaters in tandem [J].Ocean Engineering,2004,31(10):1325-1335.

[12]Hsu H,Wu Y.Scattering of water wave by a submerged horizontal plate and a submerged permeable breakwater[J].Ocean Engineering,1998,26(4):325-341.

[13]Wu Y T,Hsiao S C.Propagation of solitary waves over a submerged permeable breakwater[J].Coastal Engineering,2013, 81:1-18.

[14]王新志,汪 稔,孟庆山,等.南沙群岛珊瑚礁礁灰岩力学特性研究[J].岩石力学与工程学报,2008,27(11):2221-2226. Wang Xinzhi,Wang Ren,Meng Qingshan,et al.Research on characteristics of coral reef calcareous rock in Nansha islands [J].Chinese Journal of Rock Mechanics and Engineering,2008,27(11):2221-2226.

Study on wave motion over submerged reefs

WANG Ke,CHEN Yu-chao,SHI Peng-fei,BIAN Jiang
(State Key Laboratory of Structural Analysis for Industrial Equipment,Department of Engineering Mechanics, Dalian University of Technology,Dalian 116024,China)

Based on wave diffraction theory,boundary element method is applied to study wave motion over submerged reefs.The transmission coefficient,reflection coefficient under different conditions such as permeability,number of arrays and the lagoon’s depth are obtained.It is found that,porous reefs have less wave elimination effect than impermeable reefs.When the porosity of reefs is bigger,their wave elimination ability will become worse.A single reef is only efficient on the wave elimination of long waves,while an array of reefs have an efficient wave elimination effect on medium waves.Lagoon reef’s wave elimination ability is determined by lagoon’s depth.The wave elimination effect of lagoon reef on medium and short waves will get better when lagoon’s depth increases.But the elimination effect will show little change when lagoon’s depth reaches a certain value.

permeable reefs;boundary element method;wave transmission and reflection coefficient; lagoon

U661.1

A

10.3969/j.issn.1007-7294.2016.08.005

1007-7294（2016）08-0964-09

2016-05-09

国家重点基础研究发展计划（2013CB036101）；国家自然科学基金（51379037）

王 科（1970-），男，副教授，E-mail:kwang@dlut.edu.cn；陈彧超（1990-），男，硕士研究生。