不等间距分舱结构声辐射特性研究

刘文玺，周其斗

（海军工程大学 舰船工程系，武汉430033）

不等间距分舱结构声辐射特性研究

刘文玺，周其斗

（海军工程大学 舰船工程系，武汉430033）

研究舱段结构振动、声辐射特性随分舱形式改变的变化规律，对潜艇结构声学优化设计具有十分重要的意义。从结构声学设计的角度出发，在保持相邻两个舱段总长度不变的情况下，调整两个舱段的长度，采用结构有限元法、结构有限元耦合流体边界元方法，以辐射声功率、湿表面均方法向速度和辐射效率作为衡量结构噪声辐射能力的主要衡量指标，系统地研究整个结构振动和声辐射特性。在流体部分的计算中，采用网格重叠算法，以提高计算效率。通过调整分舱形式，在一定频段，改变了整个舱段结构振动声学传递函数的谱峰频率，降低了谱峰幅值，因此，可以通过改变分舱形式以改变舱段结构声学特性，使设备激振力的谱峰频率与结构振动声学传递函数的谱峰频率错开，实现对辐射噪声的控制。

结构声学；优化设计；振动和声辐射；谱峰频率；声学传递函数

0 引 言

舱段结构水下的振动与声辐射是潜艇结构—流体耦合振动系统的一个组成部分，舱段结构振动、声辐射特性的优劣直接影响了整个潜艇结构振动和声辐射特性的优劣，因此，研究舱段的振动、声辐射特性随结构参数的变化规律，对潜艇结构降噪设计和结构声学优化具有十分重要的意义。

迄今为止，对圆柱壳体结构振动和声辐射问题已经进行了大量的研究，计算方法主要有解析法和数值算法。对于简单的圆柱壳结构在理想流场中的声辐射问题，采用解析法能够比较快速、准确地分析结构的声辐射机理和特性[1-3]，并且可以用来验证数值方法的有效性[4-6]。刘涛等[7]用解析法研究了弹性圆柱壳在内壁简谐法向线力激励下的声辐射特性，分析了水中结构的声辐射机理，同时验证了水下结构共振声辐射理论；对于较复杂的圆柱壳结构，通常采用数值计算法。陈美霞[8]和商德江[9]用有限元结合边界元法研究了在不同激振力以及敷设阻尼材料的情况下，双层加肋圆柱壳在流场中的振动和声辐射性能。采用有限元法、边界元法和统计能量分析法可以比较方便地研究纵向加肋圆柱壳的模态密度、声辐射效率[10]、深水中复合材料圆柱壳的声辐射[11]、圆柱壳体在流场中受激振动及声辐射效率[12]。吴培荣[13]研究了双层壳间环形实肋板之间的耦合作用，以及壳间水层、实肋板与内外壳体的耦合作用，建立了有限长双层加肋圆柱壳体的振动声辐射模型，数值分析了激励力作用位置、肋板数目等对声辐射性能的影响。彭旭等[14]从Flügge薄壳理论和Helmholtz波动方程出发，根据模态叠加原理推导了有限长加筋圆柱壳受机械力和内部声源简谐激励下的“内部声腔—加筋柱壳—外部声场”耦合方程，比较了点力和点声源作用时圆柱壳的声辐射特性以及传递损失。

对结构的振动和声辐射的研究，最终归结到结构的减振降噪，近些年，许多学者在这方面进行了积极、有效的研究。在圆柱壳体合适的部位添加阻振质量，能够改变结构的模态，从而降低了壳体结构声辐射功率[15]。Johnson等[16]对复合材料圆柱壳结构内部铺层角度进行优化，使内部平均噪声水平降低了2 dB。Denli等[14-15]研究了外部声源激励下夹心圆柱壳声传输和声辐射优化问题。改变圆柱壳板的厚度和分布，能够改变圆柱壳结构的整体刚度，从而改变结构的振动和声辐射特性，通过壳板厚度的优化分布，可以有效地降低圆柱壳体的声辐射功率[19]。Bojczuk等[20]运用动力响应灵敏度信息进行了肋骨的分布优化研究，并在此基础上对肋骨的外形进行了优化。陈炉云等[21]以有限元法和边界元法为基础，对肋骨的分布和尺寸参数进行优化分析，得到了声辐射较小的加肋板结构，取得了较好的结论。

上述研究主要集中在：（1）圆柱壳体结构的振动、声辐射的计算方法；（2）阻尼材料对圆柱壳体振动、声辐射的影响；（3）肋骨等局部结构的改变对圆柱壳体振动、声辐射的影响。

在仔细学习前人研究成果的基础上，本文从以下方面对舱段结构的振动、声辐射问题做了深入的研究：从结构声学设计的角度出发，以控制噪声辐射为基本任务，以改变整个舱段结构分舱形式为方法，系统地研究结构整体的振动、声辐射特性，目的是改变舱段结构整体振动声学传递函数的谱峰频率，降低谱峰幅值。通过改变舱段结构的的声学特性，使设备激振力的谱峰频率与结构振动声学传递函数的谱峰频率错开，从而实现对辐射噪声的控制。为提高流体部分的计算效率，将网格重叠算法用于结构流固耦合的计算中。

1 基本方程

1.1 计算模型

要研究的实际舱段结构模型如图1所示。

中间的舱壁将整个结构分成两个舱段。结构的几何参数：整个舱段结构沿轴向总长度是L，柱壳直径是D，柱壳上肋骨间距是L1，肋骨腹板、面板的板厚和高度分别是t1、t2、h1、h2，柱壳板厚是t3，其中，D/L=0.487，L1/L=0.038 5，h1/D=0.029 7，h2/D=0.015 8，t1/h1=0.070 8，t2/h2=0.200，t3/D=0.003 68，两端舱壁设计成轻舱壁结构，中间舱壁设计成强舱壁结构。

1.2 结构—流体耦合方程

水下结构振动与辐射噪声问题是一个流体-结构相互作用的流固耦合问题。考虑如图2所示的结构-流体相互作用的系统：S0表示弹性薄壳结构，Ωo表示流体外域，流体外域充满密度为ρo的声介质，其声速为co。若系统进入稳态，角频率为ω，则波数ko=ω2/co。

对结构域采用有限元离散，对外域流体采用边界元法以获得附加质量和阻尼系数，将附加质量和附加阻尼叠加到结构有限元质量矩阵和阻尼矩阵上，建立了考虑流体耦合作用的有限元结构动力响应方程，如（1）式所示，从而实现流固耦合计算，进而使用边界元方法计算结构的辐射声场。

图2 流体—结构相互作用系统Fig.2 Fluid-structure interaction system

式中：KS为结构刚度矩阵；MS为结构质量矩阵；CS为结构阻尼矩阵为节点位移向量为直接作用在结构上的节点力；矩阵即为外域流体对结构作用所产生的附加质量和附加阻尼矩阵。

一旦得到结构位移，可提取结构-外域流体交接面上的节点位移，从而得到物面法向位移向量，进一步计算声场声压。上述公式的具体推导过程参见文献[22]。

为提高流体部分的计算效率，将网格重叠算法用于结构流固耦合的计算中。网格重叠算法是在流固耦合的边界上不再使用有限元网格作为边界元网格，而是重新定义一套比有限元网络要粗得多的边界元网格，即在有限元网格上重叠了一套粗的边界元网格。在本文的计算频段内，由于声波波长远大于结构弯曲波振动的波长，因此，采用网格重叠算法是合适的。

1.3 振动与声学传递函数

舱段结构与流体耦合振动所组成的是一个线性系统，对舱段结构声学特性的研究可以归结为传递函数特性的研究，为了衡量舱段结构的噪声辐射能力，采用辐射声功率，湿表面均方法向速度和辐射效率三个指标作为主要衡量指标。

辐射声功率是声源机械效率中的有效部分，壳体表面的辐射声功率大小反映了壳体表面辐射声波的本领高低；壳体表面的均方法向速度反映了壳体在流场中的结构响应，同时也表征了声源振动的平均速度；辐射效率表示壳体表面辐射声能的效率。它们分别定义如下：

辐射声功率：

均方法向速度：

辐射效率：

相应地可以定义声功率级、均方法向速度级和辐射效率级：

2 简化模型分析

在用有限元法对整个结构进行分析之前，先对模型进行简化，初步估计结构固有频率变化规律。

2.1 整体结构固有频率估算

要研究的实际结构模型如图1所示，中间的舱壁将整个结构分成两个舱段，一般地，舱壁刚性远大于舱段结构的其他部分，质量又比较大，因此，整个结构看做是两端简支的等截面梁，中间的舱壁简化为质量点，可向两端移动，这里暂时不考虑梁的质量，整个系统简化成如图3所示的单自由度系统，该单自由度系统弯曲振动刚度系数如下式所示，

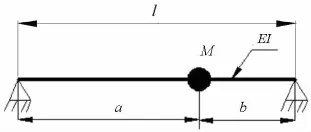
图3 简化模型Fig.3 Simplified model

图4 固有频率变化曲线图Fig.4 Curve of natural frequency changing with a

固有频率是

由（7）式和（8）式可知，固有频率随着质量点向梁的端点移动而增大，而且增大的速度在增加。固有频率随a的变化曲线如图4所示。

2.2 舱段的固有频率估算

将左端（或右端）舱段简化为两端简支的均匀直杆，其弯曲自由振动一阶固有频率由（9）式得到，振型如图5所示。

图5 均匀直杆一阶振型Fig.5 First mode shape of straight rod

式中：m表示直杆单位长度的质量，I表示直杆剖面惯性矩，l表示直杆的长度。

令左右舱段的长度分别为a和l-a，弯曲自由振动一阶固有频率分别是γ1和γ2，则固有频率比是

由（11）式和（12）式可知，随着a的增大，左右两舱段固有频率相差越来越大，而且频率差增大的速度在增加，其结果是两段结构不会同时发生共振，而且当外界激振力频率与其中一个舱段结构固有频率接近时，另一端舱段结构可以起到抑制它的振动的作用。固有频率比随a的变化曲线如图6所示。

根据上述分析，可以推断，整个结构的二阶弯曲振动（近似呈一个弯曲波形）应该以长的那段舱段振动为主，因此振动固有频率也应该与长的那段舱段振动固有频率接近，根据公式（9），整个结构的二阶弯曲振动固有频率随着中间舱壁向一端移动而减小。

图6 固有频率比变化曲线图Fig.6 Curve of natural frequency ratio changing with a

3 不等间距分舱结构在真空中的振动响应分析

图7 激振力在长舱段一端的均方法向速度Fig.7 Mean square normal velocities under force on the end of longer cabin

根据公式（6）和公式（10），可以推断，采取不等间距分舱的方法能够改变图1所示整个结构的振动固有频率，也能够调开相邻舱段的共振频率。结构声学设计的另一个重要目的是减小振动，因此，还要通过具体的计算，考察结构的振动传递函数的变化规律，即壳体湿表面均方法向速度峰值的变化规律。

3.1 结构模型

结构模型如图1所示，两个舱段总长保持不变，是L，两舱之间的舱壁由整个结构的正中间开始，以L1为步长，向一端移动，直至移动总长6L1，计算每次移动时，整个结构的振动情况，并进行比较。

3.2 结构在真空中的振动响应

当大小为1N的垂向激振力分别作用在长舱段一端舱壁上（图1左端）和短舱段一端舱壁上（图1右端）时，结构湿表面振动均方法向速度响应分别如图7和图8所示，从图中可以看出，两种情况曲线的变化规律是相似的。

根据图7和图8的曲线变化规律情况，可以看出，计算结果有如下的三个特点：（1）第一谱峰频率点随着偏移量的增加向高频移动；（2）第二谱峰频率点随着偏移量的增加向低频移动；（3）第二谱峰值随偏移量的增加而减小。下面对上述三个特点出现的原因进行逐个解释。

首先解释第一谱峰频率点随着偏移量的增大向高频移动的原因。

以激振力作用在长舱段一侧为例，将不同偏移量的结构整体弯曲振动第一阶固有频率和整体振动第一谱峰频率列出，如表1所示，将不同偏移量的结构整体弯曲振动第一阶固有频率振型云图列出，如图9-12所示，由于云图形状是类似的，限于篇幅，只列出其中的4个。

由表1和图9-12可知，第一谱峰频率出现在结构整体弯曲振动第一阶固有频率处，振型是半个弯曲波形，低频振动表现的是梁式振动。根据2.1节简化模型的固有频率随质量点向一端移动的变化情况可知，随着舱壁向一端移动，结构整体弯曲振动的第一阶固有频率增大，因此，第一谱峰频率随着偏移量的增大而向高频移动是正确的。在这个算例中变化不是很明显，主要因为中间舱壁质量相对于圆柱壳结构还是较小的，另外，外壳的刚度还不够大，因此，在后续的研究中，可通过调整圆柱壳结构和舱壁的质量比、尽量增加外壳的刚度，使固有频率向高频移动的效果更明显一些。

图8 激振力在短舱段一端的均方法向速度Fig.8 Mean square normal velocities under force on the end of shorter cabin

表1 结构整体弯曲振动第一阶固有频率和整体振动第一谱峰频率比较Tab.1 Comparison between first order natural frequency and first peak value frequency

图9 中间舱壁偏移0的整体弯曲振动第一阶固有频率振型图Fig.9 First order natural frequency vibration model of whole structure for 0 offset of middle bulkhead

图10 中间舱壁偏移2L1的整体弯曲振动第一阶固有频率振型图Fig.10 First order natural frequency vibration model of whole structure for 2L1offset of middle bulkhead

根据表1和图9-12可知，第一谱峰频率出现在结构整体弯曲振动第一阶固有频率附近，整体振动引起谱峰。换句话说，只有调整整体的结构阻抗，才最有可能改变结构低阶振动性能。

在上面的算例中，中间的舱壁是强舱壁，为了使上述的结构更具一般性，将上述强舱壁改成轻舱壁，进行同样的计算，结论和上述结论是相似的，限于篇幅的原因，这里就不列出。

下面解释第二谱峰频率点随着偏移量的增加向低频移动的原因。

以激振力作用在长舱段一侧为例，将不同偏移量的结构整体弯曲振动第二阶固有频率和整体振动第二谱峰频率列出，如表2所示，将不同偏移量的结构整体弯曲振动第二阶固有频率振型云图列出，如图13-16所示，由于云图形状是类似的，限于篇幅，只列出其中的4个。

图11 中间舱壁偏移4L1的整体弯曲振动第一阶固有频率振型图Fig.11 First order natural frequency vibration model of whole structure for 4L1offset of middle bulkhead

图12 中间舱壁偏移6L1的整体弯曲振动第一阶固有频率振型图Fig.12 First order natural frequency vibration model of whole structure for 6L1offset of middle bulkhead

表2 结构整体弯曲振动第二阶固有频率和整体振动第二谱峰频率比较Tab.2 Comparison between second order natural frequency and second peak value frequency of vibration response

图13 中间舱壁偏移0的整体弯曲振动第二阶固有频率振型图Fig.13 Second order natural frequency vibration model of whole structure for 0 offset of middle bulkhead

图14 中间舱壁偏移2L1的整体弯曲振动第二阶固有频率振型图Fig.14 Second order natural frequency vibration model of whole structure for 2L1offset of middle bulkhead

图15 中间舱壁偏移4L1的整体弯曲振动第二阶固有频率振型图Fig.15 Second order natural frequency vibration model of whole structure for 4L1offset of middle bulkhead

图16 中间舱壁偏移6L1的整体弯曲振动第二阶固有频率振型图Fig.16 Second order natural frequency vibration model of whole structure for 6L1offset of middle bulkhead

由表2和图13-16可知，第二谱峰频率出现在结构整体弯曲振动第二阶固有频率附近，振型是一个弯曲波形，低频振动表现的是梁式振动。根据2.2节的阐述，整个结构的二阶弯曲振动应该以长的舱段振动为主，因此振动固有频率也应该与长的舱段振动固有频率接近，根据公式（9），整个结构的二阶弯曲振动固有频率随着中间舱壁向一端移动而减小。

下面解释第二谱峰值随偏移量的增加而减小的原因。

与等间距分舱结构（中间舱壁偏移量等于0）振动响应相比，采取不等间距分舱结构形式，振动响应第二谱峰值普遍减小，而且，第二谱峰值随偏移量的增加而减小的趋势明显，主要由于以下原因：当相邻两个舱段长度相差越大，固有频率相差就越大，如果把两个舱段看作两个大的振动源，那么它们是不相干的，两端结构互相抑制彼此振动，起到了控制整个结构的谱峰幅值的作用。

4 不等间距分舱结构在水中的声辐射分析

图17 加肋圆柱钢壳主尺度和试验测试布置形式Fig.17 Dimension of a ribbed cylindrical shell and experimental installation

4.1 计算正确性和收敛性检验

通过对具有肋骨的柱体模型的计算，来进行计算正确性和收敛性检验。

本文对如图17所示的具有肋骨的柱体进行了实例计算，并与实验结果进行了比较，图中激励力4.448 2 N。具有肋骨的圆柱钢壳模型试验安装如图17所示。表3为圆柱壳的结构参数，计算时取水中声速c0=1 460 m/s。

将网格重叠算法应用于计算中，边界元网格数量由少到多，取不同数量，进行收敛性分析。

钢质柱壳被划分为6 754个有限单元，其中湿表面由5 924个三角形单元组成，边界元网格数量分别是368、612、1 184、5 924，即边界元网格数量分别是湿表面有限单元数的 1/20、1/ 10、2/10、1/1，计算结果如图18所示，图中的粗细单元数比表示边界元网格数与湿表面有限单元数比，图中粗虚线表示试验值，其余曲线表示计算值。可以看出，边界元网格数取不同值时，计算结果相差不大，收敛性较好。除个别点外，数值解与试验结果的误差除最小值以外都在5%以内，在最小值处，计算结果小于试验结果，其误差是由于环境噪声较大，信噪比不够所造成的。

表3 单层圆柱壳结构参数Tab.3 Structure parameters of single shell cylinder

图18 计算值与试验值的比较Fig.18 Comparison between numerical SPL and experimental data

4.2 水中结构声辐射的计算

采用辐射声功率，湿表面均方法向速度和辐射效率三个指标作为衡量结构的噪声辐射能力的主要衡量指标。研究随着中间舱壁向一端移动，这三个量的峰值、峰值频率变化规律，并且考察这三个量的变化规律存在哪些联系，也就是说，振动与噪声之间的关系，以期望为低辐射噪声结构的设计提供理论指导。

另外，比较真空中和水中的振动均方法向速度曲线，看是否存在联系，如峰值出现的频率点，振动减弱区域等，以期望能通过结构在真空中的振动变化规律，推算在水中的变化情况以及辐射噪声的变化情况，以便为结构的初步设计提供理论指导。

4.2.1 结构湿表面均方法向速度变化规律

结构湿表面均方法向速度响应曲线如图19和图20所示，图19和图20分别表示大小为1 N的激振力作用在长舱段一端和短舱段一端的计算结果。计算的频率范围是10～250 Hz，在35 Hz之前，7条曲线基本是重合在一起的，在80 Hz之后，7条曲线杂糅在一起，没有明显的规律，因此取35～80 Hz一段进行研究。

两图曲线的变化规律是相似的，以图19为例进行说明：（1）总体看，随着偏移量的增加，第一谱峰频率向高频移动，第二谱峰频率向低频移动；（2）第一谱峰频率在42 Hz附近，第二谱峰频率在60 Hz附近。

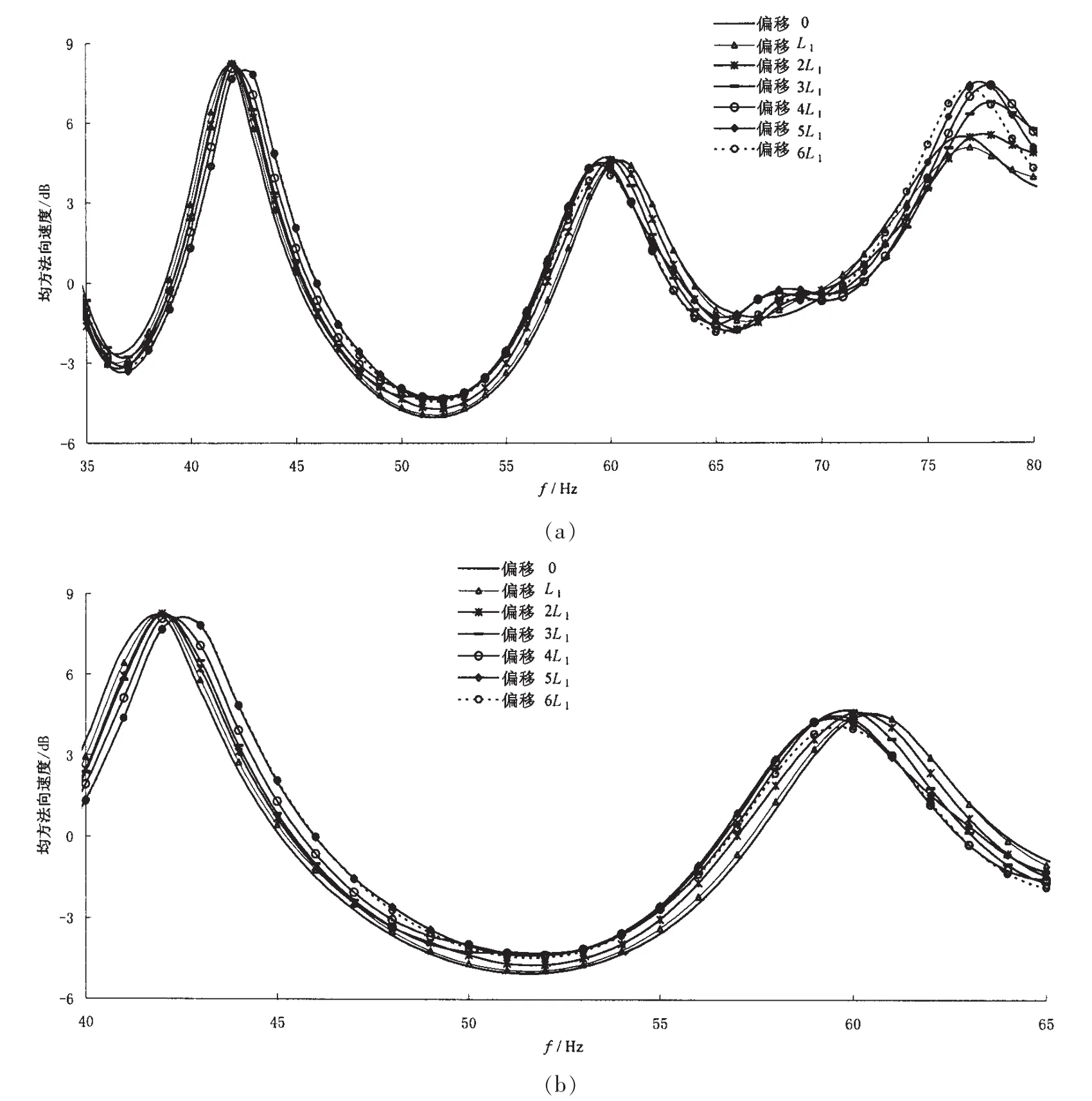
图19 激振力在长舱段一端的均方法向速度Fig.19 Mean square normal velocities under force on the end of longer cabin

由于谱峰频率的错开，使得整个曲线的变化规律可划分为如下几个区域：42 Hz以前，不等间距振动小于等间距振动；42～60 Hz之间，不等间距振动大于等间距振动；60～65 Hz之间，不等间距振动小于等距振动；70～80 Hz之间，不等间距振动远大于等间距振动。

图20 激振力在短舱段一端的均方法向速度Fig.20 Mean square normal velocities under force on the end of shorter cabin

4.2.2 水中结构辐射声功率变化规律

结构辐射声功率响应曲线如图21和图22所示，图21和图22分别表示激振力作用在长舱段一端和短舱段一端的结果。计算的频率范围是10～250 Hz，在30 Hz之前，7条曲线基本是重合在一起的，在80 Hz之后，7条曲线杂糅在一起，没有明显的规律，因此取30～80 Hz一段进行研究。

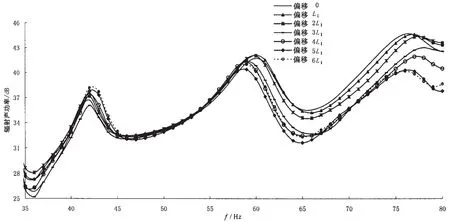
图21 激振力在长舱段一端的辐射声功率Fig.21 Acoustic radiation power under force on the end of longer cabin

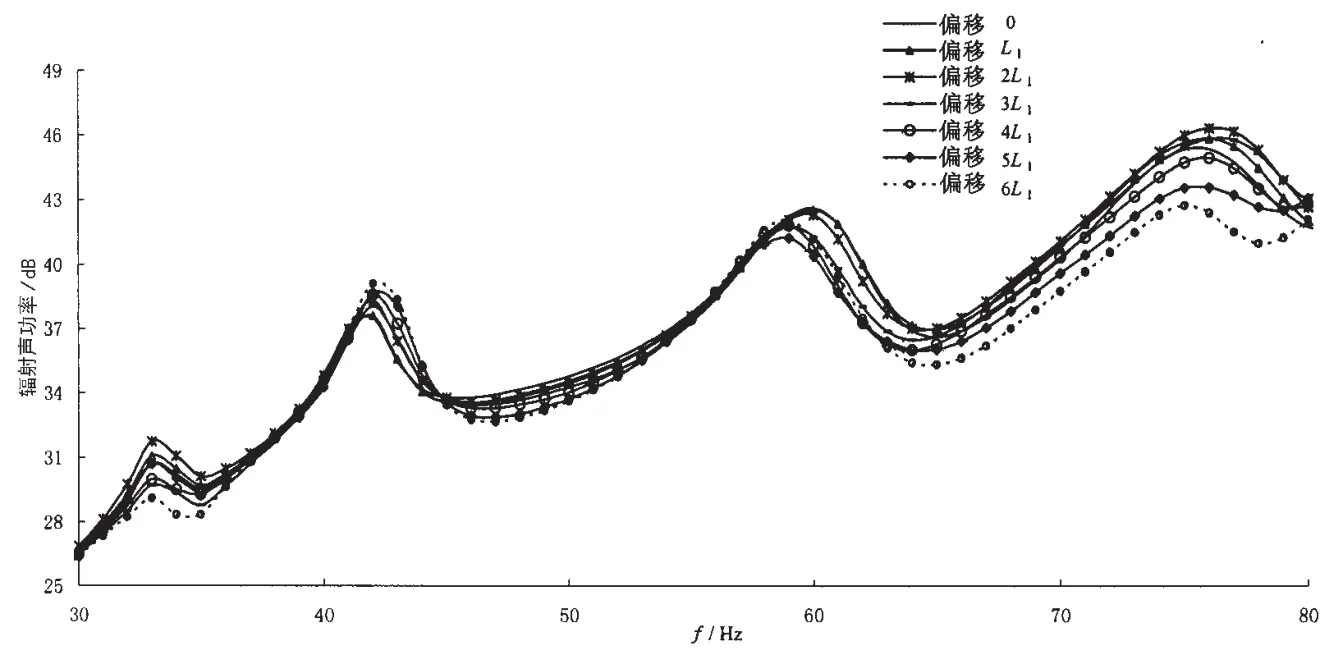
图22 激振力在短舱段一端的辐射声功率Fig.22 Acoustic radiation power under force on the end of shorter cabin

两图曲线的变化规律是相似的，以图21为例进行说明：（1）总体看，随着偏移量的增加，第一谱峰频率向高频移动，第二谱峰频率向低频移动。（2）第一谱峰频率在42 Hz附近，第二谱峰频率在60 Hz附近。

由于谱峰频率的错开，使得整个曲线的变化规律可划分为如下几个区域：60 Hz以前，不等间距辐射声功率和等间距辐射声功率相差不大；60～80 Hz之间，不等间距辐射声功率远小于等间距辐射声功率。

根据计算结果，可以看出，在振动出现峰值的频率点，结构辐射声功率也会出现峰值点，也就是说，结构振动大时，辐射噪声的能力也强。

另外，注意到，真空中与水下振动均方法向速度第一谱峰频率分别在60 Hz和42 Hz附近，第二谱峰频率分别在100 Hz和60 Hz附近，在水的作用下，结构整体振动谱峰频率向低频移动。

4.2.3 水中结构辐射效率变化规律

根据4.2.1节和4.2.2节所得到的均方法向速度和辐射声功率，计算不等间距分舱结构在水中的辐射效率，结果如图23和图24所示，图23和图24分别表示激振力作用在长舱段一端和短舱段一端的结果。

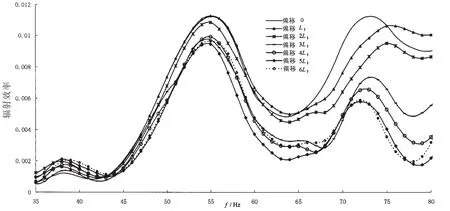
图23 激振力在长舱段一端的辐射效率Fig.23 Acoustic radiation efficiency under force on the end of longer cabin

图24 激振力在短舱段一端的辐射效率Fig.24 Acoustic radiation efficiency under force on the end of shorter cabin

5 结 论

采用不等间距分舱形式，以达到阻抗失配的目的，根据结构振动、声辐射的计算结果，得到以下结论：

（1）在真空中，通过调整分舱形式，可以改变结构整体弯曲振动响应的谱峰频率和谱峰幅值，尤其是低频响应的谱峰频率和谱峰幅值；

（2）在水中，通过调整分舱形式，同样可以改变振动响应、辐射声功率的谱峰频率和谱峰幅值。在结构振动出现峰值的频率点，辐射声功率也会出现峰值点，也就是说，结构振动大时，辐射声能的能力也强；

（3）在设计的时候，要根据实际的应用要求来调整结构形式，达到设计者的目的。

（4）本文的研究方法，可以推广到肋骨不等间距排列对结构振动、声辐射影响的研究中。

[1]汤渭霖,何兵蓉.水中有限民加肋圆柱壳体振动和声辐射近似解析解[J].声学学报,2001,26(1):1-5. Tang Weilin,He Bingrong.Approximate analytic solution of vibration and sound radiation from stiffened finite cylindrical shells in water[J].Acta Acustica,2001,26(1):1-5.

[2]陈美霞,骆东平.双层柱壳在流场中辐射声场压力的解析解[J].应用数学和力学,2002,23(4):415-421. Chen Meixia,Luo Dongping.Analytical solution of radiation sound pressure of double cylindrical shells in fluid medium [J].Applied Mathematics and Mechanics,2002,23(4):415-421.

[3]Guan Shanshan,Deng Haihua.Sound radiation characteristics of a submerged stiffened cylindrical shells subjected to internal acoustic excitations[J].Journal of Ship Mechanics,2014,18(3):328-343.

[4]Berot F,Peseux B.Vibra-acoustic behavior of submerged cylindrical shells:Analytical formulation and numerical model [J].Journal of Fluids and Structures,1998,12(8):959-1003.

[5]夏齐强,楼伟锋.双层圆柱壳结构减振设计及模型试验研究[J].船舶力学,2016,20(1-2):148-158. Xia Qiqiang,Lou Weifeng.Study on vibration reduction design for double cylindrical shell and model testing[J].Journal of Ship Mechanics,2016,20(1-2):148-158.

[6]杨晓刚,林 立.径向激励作用下有限长双层圆柱壳声振传递特性研究[J].船舶力学,2016,19(5):600-608. Yang Xiaogang,Lin Li.Sound and vibration transmission characteristic of finite length double cylindrical shells under radial excitation[J].Journal of Ship Mechanics,2015,19(5):600-608.

[7]刘 涛,范 军,汤渭霖.水中弹性圆柱壳的共振声辐射[J].声学学报,2002,27(1):62-66. Liu Tao,Fan Jun,Tang Weilin.Resonance radiation theory of a submerged elastic cylindrical shells[J].Acta Acustica, 2002,27(1):62-66.

[8]陈美霞,骆东平.激励力对双层圆柱壳声辐射性能的影响[J].船舶力学,2005,9(2):124-130. Chen Meixia,Luo Dongping.Effect of driving forces property on characteristics of sound radiation from finite double cylindrical shell[J].Journal of Ship Mechanics,2005,9(2):124-130.

[9]商德江,何祚镛.加肋双层圆柱壳振动声辐射数值计算分析[J].声学学报,2001,26(3):193-201. Shang Dejiang,He Zuoyong.The numerical analysis of sound and vibration from a ring-stiffened cylindrical double-shell by FEM and BEM[J].Acta Acustica,2001,26(3):193-201.

[10]Ramachandran P,Narayanan S.Evaluation of modal density,radiation efficiency and acoustic response of longitudinally stiffened cylindrical shell[J].Journal of Sound and Vibration,2007,304(1-2):151-174.

[11]倪 樵,艾国庆.深水复合材料圆柱壳声辐射的数值分析[J].华中科技大学学报,2006,34(12):77-79. Ni Qiao,Ai Guoqing.Numerical analysis of acoustic radiation by composite elliptic cylindrical shell submerged in deep water[J].J Huazhong Univ.of Sci.&Tech.(Nature Science Edition),2006,34(12):77-79.

[12]贺 晨,盛美萍.圆柱壳体振动声辐射效率数值计算分析[J].噪声与振动控制,2006,26(4):51-54. He Chen,Sheng Meiping.The numerical analysis of vibration and sound radiation efficiency from a cylindrical shell[J]. Noise and Vibration Control,2006,26(4):51-54.

[13]吴培荣,范 军.有限长双层加肋圆柱壳体的声辐射特性[J].船舶工程,2009,31(4):13-15. Wu Peirong,Fan Jun.Sound radiation characteristics of finite double-layer annular-plate stiffened cylindrical shells[J]. Ship Engineering,2009,31(4):13-15.

[14]彭 旭,关姗姗.内部声激励下加筋圆柱壳的声辐射特性分析[J].固体力学学报,2007,28(4):355-361.Peng Xu,Guan Shanshan.Sound radiation analysis of stiffened cylindrical shells excited by interior sound excitation[J]. Acta Mechanica Solida Sinica,2007,28(4):355-361.

[15]Constans E W,Belegundu A D,Koopmann G H.Design approach for minimizing sound power from vibrating shell structure[J].AIAA.Journal,1998,36(2):134-139.

[16]Johnson W M,Cunefare K A.Structural acoustic optimization of a composite cylindrical shell using FEM/BEM[J].Journal of Vibration and Acoustics,2002,124:(7):410-413.

[17]Denli H,Sun J Q.Structural-acoustic optimization of sandwich structures with cellular cores for minimum sound radiation[J].Journal of Sound and Vibration,2007,301(1-2):93-105.

[18]Denli H,Sun J Q.Structural-acoustic optimization of cylindrical shells for minimum interior sound transmission[J].Journal of Sound and Vibration,2008,316(1-5):32-49.

[19]刘宝山,赵国忠,王 剑.基于设计灵敏度分析的圆柱壳声辐射优化[J].大连理工大学学报,2011,51(3):313-319. Liu Baoshan,Zhao Guozhong,Wang Jian.Acoustic radiation optimization of cylinder shell based on design sensitivity analysis[J].Journal of Dalian University of Technology,2011,51(3):313-319.

[20]Bojczuk D,Szteleblak W.Optimization of layout and shape of stiffeners in 2D structures[J].Comput.Struct,2008,86(13): 1436-1446.

[21]陈炉云,张裕芳,李英辉.肋骨分布对肋板声辐射影响及分布优化分析[J].武汉理工大学学报（交通科学与工程版）, 2011,35(1):24-28. Chen Luyun,Zhang Yufang,Li Yinghui.Acoustic radiation influence of stiffeners layout and layout optimization analysis [J].Journal of Wuhan University of Technolog(Transporta-ti on Science&Engineering),2011,35(1):24-28.

[22]Zhou Qidou,Joseph P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration,2005,283:853-873.

Study on characteristics of acoustic radiation from the cabin structure with nonuniform subdivision

LIU Wen-xi,ZHOU Qi-dou
(Department of Naval Architecture Engineering,Naval University of Engineering,Wuhan 430033,China)

Study on the relation between the vibration and acoustic radiation from the cabin structures and the method of cabin division is very important for the structure-acoustic optimization design of the submarine.From the angle of the structure-acoustic design,in the condition of keeping the total length of two cabins,adjusting the length of the two cabins respectively,and the structural finite element method,and the structural finite element coupled fluid boundary element method are adopted for the numerical calculation,and the acoustic radiation power,mean square normal velocities of the wet surface and the acoustic radiation efficiency are adopted as the main indexes to estimate the acoustic radiation ability from the subroutine structures and the characteristics of the vibration and acoustic radiation from the whole structure systemically.In the calculation about the fluid,the‘mesh superposition method’is used to improve the calculating efficiency.By adjusting the cabin division method,in some frequency band,the peak value frequencies of the transfer functions of the vibration and acoustic radiation are changed,and the peak value is reduced.The results show that the acoustic characteristics of the cabin structure can be changed by adjusting the above method,so that the exciting force of the machines and the spectral peak frequencies of the transfer functions are separated,as a result,the noise and vibration are controlled.

acoustic-structure;optimization design;vibration and acoustic radiation; spectral peak frequency;acoustic transfer function

O422.6

A

10.3969/j.issn.1007-7294.2016.08.014

1007-7294（2016）08-1045-14

2015-12-02

*****演示验证项目（*2011001/101）

刘文玺（1977-），男，博士后，E-mail:wxliu777@163.com；周其斗（1962-），男，教授，博士生导师。