弹性边界约束的正交加肋圆柱壳振动特性分析
2016-05-04曹登庆孙述鹏
刘 伦,曹登庆,孙述鹏,龙 钢
(1.哈尔滨工业大学 航天学院,哈尔滨 150001;2.西安现代控制技术研究所,西安710065)
弹性边界约束的正交加肋圆柱壳振动特性分析
刘 伦1,曹登庆1,孙述鹏1,龙 钢2
(1.哈尔滨工业大学 航天学院,哈尔滨 150001;2.西安现代控制技术研究所,西安710065)
使用Gram-Schmidt正交化构造了满足圆柱壳自由边界条件的一组正交多项式,并以此为基函数构造圆柱壳的振动位移表达式;在此基础上,基于Sanders壳体理论,利用Rayleigh-Ritz法,提出了一种用于分析弹性边界约束的正交加肋圆柱壳振动特性的方法。利用该方法,求解了两端简支的正交加肋圆柱壳的自由振动固有频率,将其与文献结果对比,验证了文中方法的正确性;该文还分析了边界各方向约束刚度对正交加肋圆柱壳振动特性的影响。研究表明,本文的方法收敛性好,计算效率高,且可用于分析受经典边界约束的加肋壳振动特性,具有很强的通用性。
正交加肋圆柱壳;弹性边界;正交多项式;振动特性;Rayleigh-Ritz法
0 引 言
正交加肋圆柱壳被广泛应用于工程结构中,比如潜艇、压力容器、航空发动机和航天器外壳等。这些壳体结构所受的动力学荷载复杂多变,其振动特性对此类结构的优化设计十分重要,因此对正交加肋圆柱壳的振动特性研究具有重要的理论意义和应用价值。
根据对肋条处理方式的不同,目前的研究方法可以分为两类。一类是将肋条的刚度和质量分布到整个壳体上,得到一个等效的正交异性圆柱壳,即所谓“Smearing-out”技术或者平均法[1-2],这类方法适用于处理加密肋圆柱壳(肋间距较小)的振动问题,但由于所用的等效方法依赖于圆柱壳振动的环向波数和肋条间距,因此,当肋条间距相对较大(加稀肋)或者振动波长小于肋条间距时,该类方法不再适用。另一类是将各肋条看作壳体上的离散单元,这类方法适用于研究加密肋和加稀肋的圆柱壳振动问题,适应性很好,因此得到了很大的发展。孟宪举等[3]根据圆柱壳的Hamilton正则方程及其半解析解法,提出了一种对圆柱壳厚度和肋条高度没有限制的有限元模型。Forsberg[4]将加环肋圆柱壳分割成壳节段和肋节段,使用传递矩阵法对加环肋圆柱壳振动特性进行了研究;Huang[5]使用导纳法对两端简支的高速旋转加环肋圆柱壳进行了研究;此外,波传播法也被用于加肋圆柱壳的振动特性分析,代表性的工作有Zhang等[6]、Gan等[7]和Liu[8]等。Sun等[9]使用傅里叶级数展开,提出了一种能求解多种边界条件下旋转薄壁圆柱壳振动响应的方法;还有学者使用能量法研究加肋圆柱壳的振动问题,如Wang和Lin[10]、李学斌[11];此外,Rayleigh-Ritz法也被广泛用于研究加肋圆柱壳振动特性,例如:Jafari和Bagheri[12]研究了不均匀加肋圆柱壳的振动问题,李正良等[13]求得了正交加肋圆柱壳—球壳组合结构在固定—自由及简支—自由边界条件下的自由振动频率。第二类方法适用性好,无论加密肋还是稀肋都能得出准确的结果,但由于要分别处理多个肋条与圆柱壳之间的变形相容条件,因此这类方法往往都随着肋条数量增加而变得异常复杂。
以上文献的分析方法大都只能用于分析受经典边界条件约束(如固支、简支)的圆柱壳振动特性,鲜有针对弹性边界约束的圆柱壳振动分析方法。虽然当下的有限元软件,如ANSYS,可以用于处理弹性约束的加肋圆柱壳振动问题,但不利于对结构进行优化设计。另外,实际工程中壳体所受的复杂边界条件不能简单地考虑为经典边界条件,但可以等效为弹性支承。因此,基于以上几点,有必要提出针对弹性边界约束下的加肋圆柱壳振动分析方法。
Sun等[14]使用弹簧模任意边界,研究了转动圆柱壳的自由振动特性。在此基础上,本文将肋条看作是离散的单元作用在圆柱壳上,用Rayleigh-Ritz法推导了弹性约束下正交加肋壳的频率方程。基本步骤为:(1)基于Sanders壳体理论,写出圆柱壳、肋条的动能和应变能,以及弹性边界的应变能;(2)使用Gram-Schmidt正交化构造满足圆柱壳自由边界条件的一组正交多项式,将其作为基函数,构造柱壳中曲面振动位移函数;(3)用振动位移函数对加肋壳结构(包括弹性边界)能量进行离散,使用Rayleigh-Ritz法推导出弹性边界约束的正交加肋壳频率方程。该分析方法可以用于分析受弹性边界约束的加肋圆柱壳振动特性,在使用与经典边界条件相对应的边界约束刚度时,此方法还可用于分析受经典边界约束的加肋圆柱壳振动问题。
1 正交加肋圆柱壳振动理论分析

图1 两端弹性约束的正交加肋圆柱壳模型Fig.1 Model of orthogonal stiffened cylindrical shells constrained by elastic boundary at two ends
考虑如图1所示的长L、厚H、半径为R的薄壁正交加肋圆柱壳,环肋数量Nr,纵肋数量Ns,第i条环肋的宽度和高度分别为bri和dri,第i条纵肋的宽度和高度分别为bsi和dsi,各环肋(纵肋)尺寸一致,且均匀布置;壳两端各受一圈弹性支承约束,单位长度上的径向、切向、法向和转动方向的约束刚度分别为ku、kv、kw和kϑ。壳体材料密度为ρ,杨氏弹性模量为E,剪切模量泊松比为μ;第i条环肋的密度为ρri,杨氏弹性模量为Eri,剪切模量为Gri;第i条纵肋的密度为ρsi,杨氏弹性模量为Esi,剪切模量为Gsi。下标ri代表第i条环肋,si代表第i条纵肋。
1.1 正交加肋圆柱壳的动能和势能
设ξ=x/L,由于所考虑的圆柱壳为薄壁,故可忽略转动惯量的影响,因而圆柱壳的动能可表示为:

利用Sanders壳体理论,圆柱壳的应变能可以写成:

考虑环肋偏心和绕x、z轴的转动惯性的影响,其动能可表示为:

考虑纵肋偏心的影响,其动能可表示为:
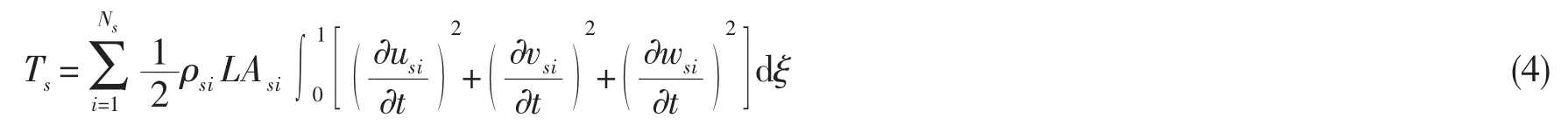
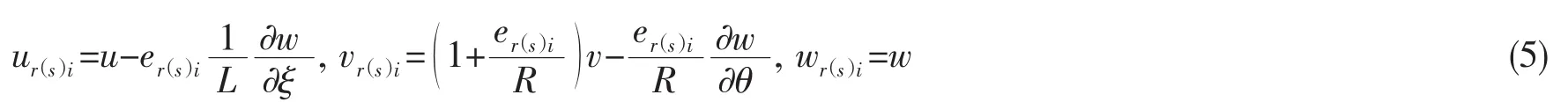
环肋的应变能为:

纵肋的应变能为:
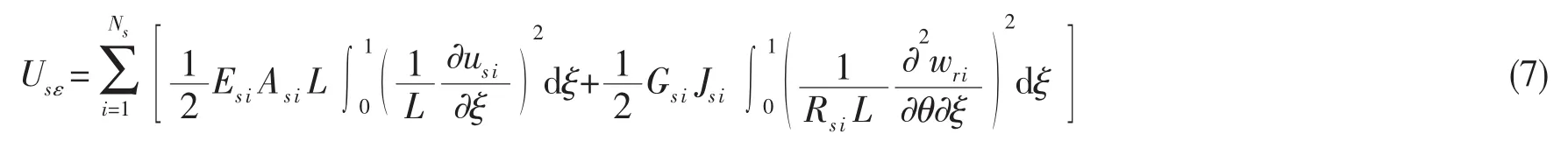

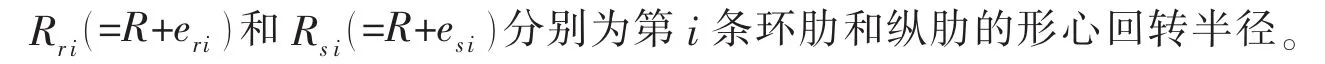
正交加肋圆柱壳两端弹性约束的势能可以写为:

其中:下标0和l分别代表圆柱壳的两端x=0和x=l。
1.2 利用Rayleigh-Ritz法推导正交加肋圆柱壳频率方程
Bhat[15]在研究矩形板的振动时首先使用正交多项式构造振型函数,Lim和Liew[16]使用正交多项式构建了圆柱壳的轴向振型函数。对于两端自由的圆柱壳,其满足几何边界条件的正交多项式组可用Gram-Schimidt正交化构造,其首项表达式如下:

根据Bhat[15]的推导,可以得到一组正交多项式:


使用由(10)、(11)式所得到的正交多项式组作为基函数,可设两端自由的圆柱壳环向波数为n时中曲面的振动位移函数表达式为:

式中:ω是正交加肋圆柱壳的固有圆频率,Nt是圆柱壳的振动位移基函数的项数,ajn、bjn和cjn是待定常数。
忽略阻尼,由能量守恒有:

将(13)式代入(14)式,由Rayleigh-Ritz法,得瑞利商:

其中:

ω*2对ajn、bjn和cjn取极小值,即:

可得到弹性边界约束下正交加肋圆柱壳的频率方程:
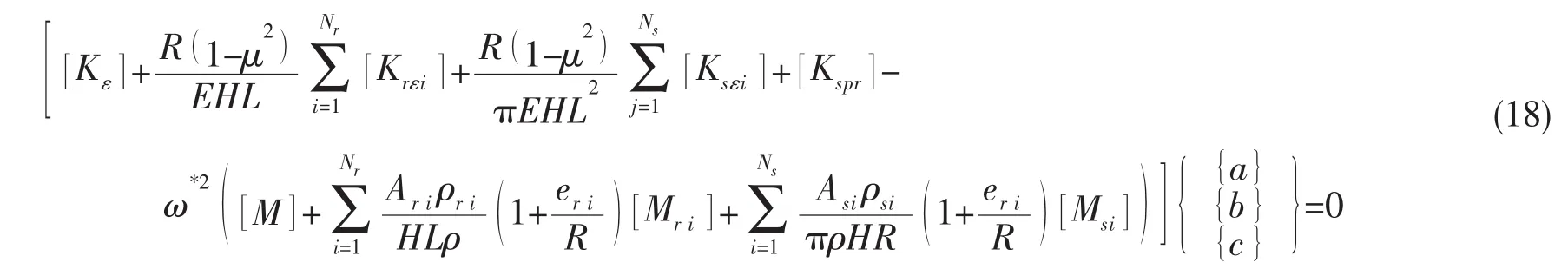

2 结果与讨论
2.1 有效性及收敛性分析
为了便于陈述,针对表1给出的具有不同材料常数、几何参数和加肋形式的正交加肋圆柱壳,分别用模型M1和M2表示。为验证本文方法的正确性,计算了模型M1的固有频率,并与已有文献结果进行了对比。模型M1两端简支,纵肋和环肋等间距布置,且偏心距一致。简支边界对应的几何边界条件为:壳两端环向和径向位移为零,也即这两个方向上的约束刚度无穷大,从(19)式可知,环向和径向无量纲约束刚度比有量纲刚度小109量级(有量纲刚度值kv、kw与E(109量级)相除),因此,取无量纲刚度时,环向和径向约束刚度为1011量级,可近似地描述无穷大的约束刚度;轴向和转动方向自由,则相应的约束刚度为零,由(19)式得在表2中列出了利用(18)式计算的轴向振型阶数m=1、环向波数n=1~5模态下模型M1的固有频率以及与现有文献结果的比较,rt表示本文Nt=13的结果与相应文献结果的相对差异。从中可以看出,由于本文和文献[17]都考虑了环肋和纵肋偏心的影响,因此本文的计算结果与文献[17]的结果最接近,相对差异不超过3%,这也说明通过使用合适的弹性边界约束刚度可以模拟简支边界,也即本文分析弹性边界下正交加肋壳的方法可用于分析受经典边界约束的加肋壳振动特性,这表明该方法具有很强的通用性。本文在表达环肋动能时还计入了转动惯性的影响,因此结果比文献[17]的更接近真实值。文献[1]、[18]和[19]运用了Love壳体理论,都未考虑肋条偏心的影响,且文献[19]用梁函数近似圆柱壳轴向振型函数,因此这三篇文献的结果与本文的存在一定差异。从表2可以看出,使用本文所提出的方法计算正交加肋圆柱壳固有频率时,振动位移基函数仅需截取Nt=7项就可得到m=1、n=1~5模态下固有频率的收敛值。

表1 模型M1/M2材料和几何参数Tab.1 Material and geometric parameters for Model 1 and Model 2
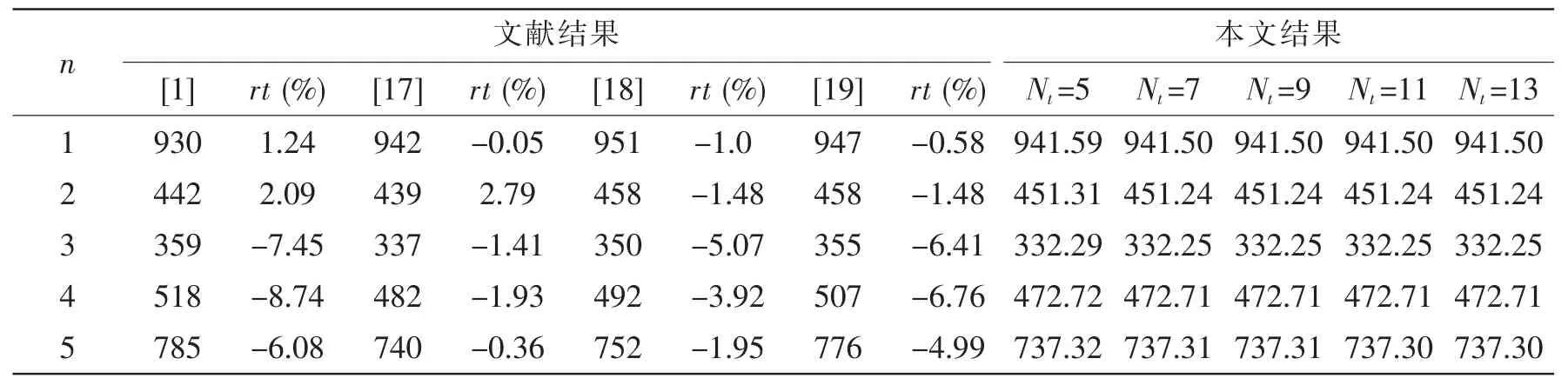
表2 模型M1频率及与文献结果的比较f(Hz)(m=1)Tab.2 Comparisons of natural frequencies with results from literature for Model 1 f(Hz)(m=1)
在计算正交加肋圆柱壳的固有频率时,截取的振动位移基函数项数越多,即Nt取得越大,计算结果就越接近精确值。因此,可以根据实际工程的需要而取适当的Nt以获得足够精确的结果。
为进一步分析本文方法的收敛性,检验其计算效率,针对某一模态,定义截取Nt项振动位移基函数时所求得的固有频率fNt的相对误差RtNt为:

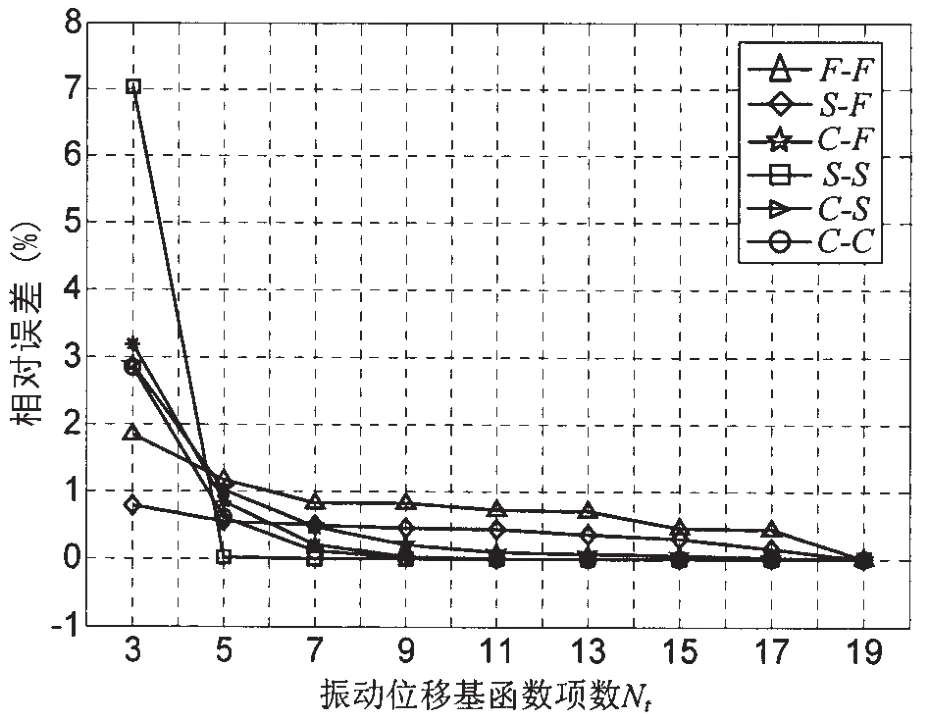
图2 模型M2固有频率在六种经典边界下的收敛性(m=1,n=2)Fig.2 Convergence of natural frequencies for Model 2 with six classical boundary conditions(m=1,n=2)
其中: fref是该模态下正交加肋圆柱壳的具有足够精度的固有频率。从表2可以看出,在m=1,n= 1~4的模态下,Nt=7、9、13时柱壳的固有频率基本保持不变,仅m=1,n=5模态下的频率发生了细微变化。因此,为了使收敛性分析更精确,本文用Nt=19时所得固有频率作为fref,即fref=f19。本文用F、S和C分别代表自由、简支和固支边界约束,借鉴对简支边界的分析,各边界条件所对应的无量纲约束刚度分别为利用(18)式计算了表1所示模型M2在六种经典边界条件下各振动位移基函数截取项(Nt=3~19)所对应的固有频率及其相对误差,如图2所示,圆柱壳模态为m=1,n=2。从图2可以看出,在各边界条件下,针对所取的模态,随着截取的振动位移基函数项数Nt逐渐增大,对应的固有频率相对于精确值的误差逐渐降低,最终有收敛于零的趋势。当Nt=7时,各边界条件所对应的固有频率的相对误差已在1%以内,而表2中针对模型M1的计算结果也是在Nt=7时就已收敛。对比图2中各条收敛曲线可以发现,就模型M2而言,在所取的模态下,简支-简支(S-S)、固支-简支(C-S)和固支-固支(C-C)所对应的固有频率收敛速度要比其他边界条件下的更快。
2.2 边界刚度对正交加肋圆柱壳固有频率的影响

图3 弹性约束和固支-简支约束下加肋壳和不加肋壳固有频率随n变化曲线(m=1)Fig.3 Variation of natural frequencies for stiffened and unstiffened shells with respect to the circumferential wavenumber n for elastic boundary and C-S boundary condition (m=1)
图3 表示了肋条和边界刚度对正交加肋圆柱壳固有频率的影响。所用壳和肋的材料及几何参数见表1模型M2,边界条件分别为固支-简支(C-S)和弹性支承,其中弹性支承所用的边界各方向无量纲约束刚度值分别为从图3可以看出,在环向波数n较小时,边界条件对加肋壳固有频率的影响很大,肋条的影响则很小,固支-简支(C-S)边界约束下的不加肋圆柱壳的固有频率甚至高于弹性支承下正交加肋圆柱壳的固有频率。随着环向波数n的增大,对不加环肋圆柱壳而言,边界条件的影响逐渐降低,n足够大时,弹性支承下的壳体固有频率与固支-简支(C-S)边界下的壳体固有频率几乎一致;对正交加肋圆柱壳而言,边界条件的影响仍然很大,弹性支承下(边界约束较弱)的正交加肋圆柱壳固有频率始终小于固支-简支(C-S)边界下加肋壳的频率;此外n较大时加肋壳的频率始终高于光壳的频率,肋条的影响逐渐增大。
假定正交加肋圆柱壳两端受相同的弹性边界约束,可得图4与图5所示的在m=1、n=2和m=2、n=5两种模态下边界各方向上的约束刚度对壳体固有频率的影响。所用模型参数见表1模型M2。综合分析图4与图5可以看出,图5(a)和(b)中壳体固有频率变化幅度要远小于图4(a)和(b)中的频率变化幅度,这表明对于高阶频率(较大的m和n,这里是m=2、n=5),边界约束刚度的影响要小很多,这一点也在图3中反映出来;另外,对不同的模态,边界各方向上的约束刚度对正交加肋圆柱壳固有频率的影响趋势一致,为简便起见,本文只具体分析图4。在图4(a)中,转动方向和轴向的无量纲约束刚度保持为0,环向和径向无量纲约束刚度从0逐渐增大到100,也即正交加肋圆柱壳的边界约束由自由-自由(F-F)逐渐发展到简支-简支(S-S)。在此过程中,环向约束刚度与径向约束刚度对壳体固有频率有着相似的影响趋势,均使得壳体固有频率逐渐增大,增大的速率先快后慢,最终趋于零。从图4(a)中可以看出,当足够大时,壳体固有频率收敛于一个值,这便是简支-简支(SS)边界下正交加肋圆柱壳的固有频率。在图4(b)中,环向和径向的无量纲约束刚度均保持在100,轴向和转动方向上的无量纲约束刚度从0逐渐增大到100,也即正交加肋圆柱壳的边界约束由简支-简支(S-S)逐渐发展到固支-固支(C-C)。在此过程中,转动方向上的约束刚度对壳体固有频率几乎没有影响,相比之下,轴向约束刚度的增加则使壳体固有频率显著增大,增大速率由慢到快再变慢。从图4(b)中可以看出,当足够大时,壳体固有频率收敛于一个值,这便是固支-固支(C-C)边界下加环肋圆柱壳的固有频率。

图4 正交加肋圆柱壳固有频率与边界约束刚度关系曲面(m=1,n=2):(a)=0,(b)=100Fig.4 Variation of natural frequencies for orthogonal stiffened cylindrical shells with respect to restraint stiffness(m=1,n=2):(a)=0,(b)=100

图5 正交加肋圆柱壳固有频率与边界约束刚度关系曲面(m=2,n=5):(a)=0,(b)=100Fig.5 Variation of natural frequencies for orthogonal stiffened cylindrical shells with respect to restraint stiffness(m=2,n=5):(a)=0,(b)=100
3 结 论
本文将肋条看作是作用在壳体上的离散单元,使用Rayleigh-Ritz法,提出了一种用于分析两端弹性约束的正交加肋圆柱壳振动特性的方法。该方法采用了Sanders壳体理论,在假设圆柱壳中曲面振动位移时,使用了一组由Gram-Schmidt正交化得到的满足圆柱壳自由边界条件的正交多项式作为基函数。验证了该方法的正确性,分析了其收敛性,并基于此方法分析了边界约束刚度对壳体固有频率的影响。研究表明:
(1)本文提出的分析方法收敛性好,计算效率高,能方便地用于加肋壳优化设计。该方法虽是针对受弹性约束的正交加肋壳提出的,但也可用于受经典边界约束的加肋壳振动特性分析,具有很强的通用性;与边界识别相结合时,该方法能用于受任意边界约束的加肋圆柱壳振动特性分析。
(2)环向波数n较小时,边界约束刚度对正交加肋圆柱壳的振动特性影响大于肋条的影响,但当n增大时,边界约束刚度的影响逐渐降低,肋条的影响增大,也即边界条件对高频影响不大。
(3)对于某一方向上的边界约束刚度,在不同模态下,对正交加肋圆柱壳固有频率有着相似的影响。环向和径向约束刚度增加,均使得壳体频率增大,增大速率逐渐降低,最终趋于零,且环向约束刚度能更有效地增大壳体频率;转动方向上的约束刚度变化对壳体频率几乎没有影响,但轴向约束刚度增加,能显著增大壳体频率,增大速率先升后降。
[1]Zhao X,Liew K M,Ng T Y.Vibrations of rotating cross-ply laminated circular cylindrical shells with stringer and ring stiffeners[J].International Journal of Solids and Structures,2002,39:529-545.
[2]Xiao H L,Liu T G,Zhang T,et al.Vibration analysis of composite cylindrical shells with stringer and ring stiffeners[J]. Journal of Ship Mechanics,2007,11(3):470-478.
[3]孟宪举,张 策,卿光辉.加筋圆柱壳的振动特性分析[J].振动工程学报,2005,18(1):36-40. Meng Xianju,Zhang Ce,Qing Guanghui.Vibration characteristics analysis of stiffened cylindrical shell[J].Journal of Vibration Engineering,2005,18(1):36-40.
[4]Forsberg K.Exact solution for natural frequencies of a ring-stiffened cylinder[C].AIAA/ASME 10th Structures,Structural Dynamics and Materials Conference,ASME Volume on Structure and Materials,1969:18-30.
[5]Huang S C,Hsu B S.Vibration of spinning ring-stiffened thin cylindrical shells[J].AIAA Journal,1992,30(9):2291-2298.
[6]Zhang X M,Liu G R,Lam K Y.Vibration analysis of thin cylindrical shells using wave propagation approach[J].Journal of Sound and Vibration,2001,239(3):397-403.
[7]Gan L,Li X B,Zhang Z.Free vibration analysis of ring-stiffened cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration,2009,326:633-646.
[8]Liu X,Liang B,Li R,et al.Effect of stiffening parameters on vibration characteristics of fluid-filled cylindrical shells with ring-stiffener[J].Journal of Ship Mechanics,2015,19(3):294-302.
[9]Sun S,Chu S,Cao D.Vibration characteristics of thin rotating cylindrical shells with various boundary conditions[J].Journal of Sound and Vibration,2012,331:4170-4186.
[10]Wang R T,Lin Z X.Vibration analysis of ring-stiffened cross-ply laminated cylindrical shells[J].Journal of Sound and Vibration,2006,295:964-987.
[11]李学斌.环肋圆柱壳自由振动分析的能量法[J].船舶力学,2001,5(2):73-81. Li Xuebin.Energy method for free vibration analysis of ring-stiffened cylindrical shells[J].Journal of Ship Mechanics, 2001,5(2):73-81.
[12]Jafari A A,Bagheri M.Free vibration of non-uniformly ring-stiffened cylindrical shells using analytical,experimental and numerical methods[J].Thin-Walled Structures,2006,44:82-90.
[13]李正良,胡 浩,于 伟.正交加筋圆柱壳—球壳组合结构自由振动分析[J].振动与冲击,2015,34(22):129-137. Li Zhengliang,Hu Hao,Yu Wei.Free vibration of joined and orthogonally stiffened cylindrical-spherical shells[J].Journal of Vibration and Shock,2015,34(22):129-137.
[14]Sun S,Cao D,Han Q.Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the Rayleigh-Ritz method[J].International Journal of Mechanical Sciences,2013,68:180-189.
[15]Bhat R B.Natural frequencies of rectangular plates using characteristic orthogonal polynomials in Rayleigh-Ritz method [J].Journal of Sound and Vibration,1985,102:493-499.
[16]Liew K M,Lim C W.Vibratory characteristics of cantilevered rectangular shallow shells of variable thickness[J].AIAA Journal,1994,32(2):387-396.
[17]Mustafa B A J,Ali R.An energy method for free vibration analysis of stiffened circular cylindrical shells[J].Computer and Structures,1989,32(2):335-363.
[18]Lee Y S,Kim Y W.Vibration analysis of rotating composite cylindrical shells with orthogonal stiffeners[J].Computers and Structures,1998,69:271-281.
[19]Lee Y S,Kim Y W.Effect of boundary conditions on natural frequencies for rotating composite cylindrical shells with orthogonal stiffeners[J].Advances in Engineering Software,1999,30:649-655.
附录
Vibration analysis of orthogonal stiffened cylindrical shells constrained by elastic boundary
LIU Lun1,CAO Deng-Qing1,SUN Shu-peng1,LONG Gang2
(1.School of Astronautics,Harbin Institute of Technology,Harbin 150001,China; 2.Xi’an Modern Control Technology Research Institute,Xi’an 710065,China)
A set of characteristic orthogonal polynomials satisfying free-free boundary condition is constructed directly by employing Gram-Schmidt procedure,and then is employed to represent the general formulations for the displacements in any axial mode of free vibrations for shells.Based on Sanders’shell theory,a method using to analyze vibration characteristics for orthogonal stiffened cylindrical shells constrained by elastic boundary is proposed by employing Rayleigh-Ritz method.Comparing with the available analytical results for a simply supported orthogonal stiffened cylindrical shell,the method proposed in this paper is verified and it is proved that this method can also be used to analyze vibration characteristics of shells with classical boundaries.Strong convergence is observed from convergence study.Further,the effects of the restraint stiffness for elastic boundary in axial,circumferential,radial and rotational directions, on the natural frequencies are studied.
orthogonal stiffened cylindrical shells;elastic boundary;characteristic orthogonal polynomials; vibration characteristics;Rayleigh-Ritz method


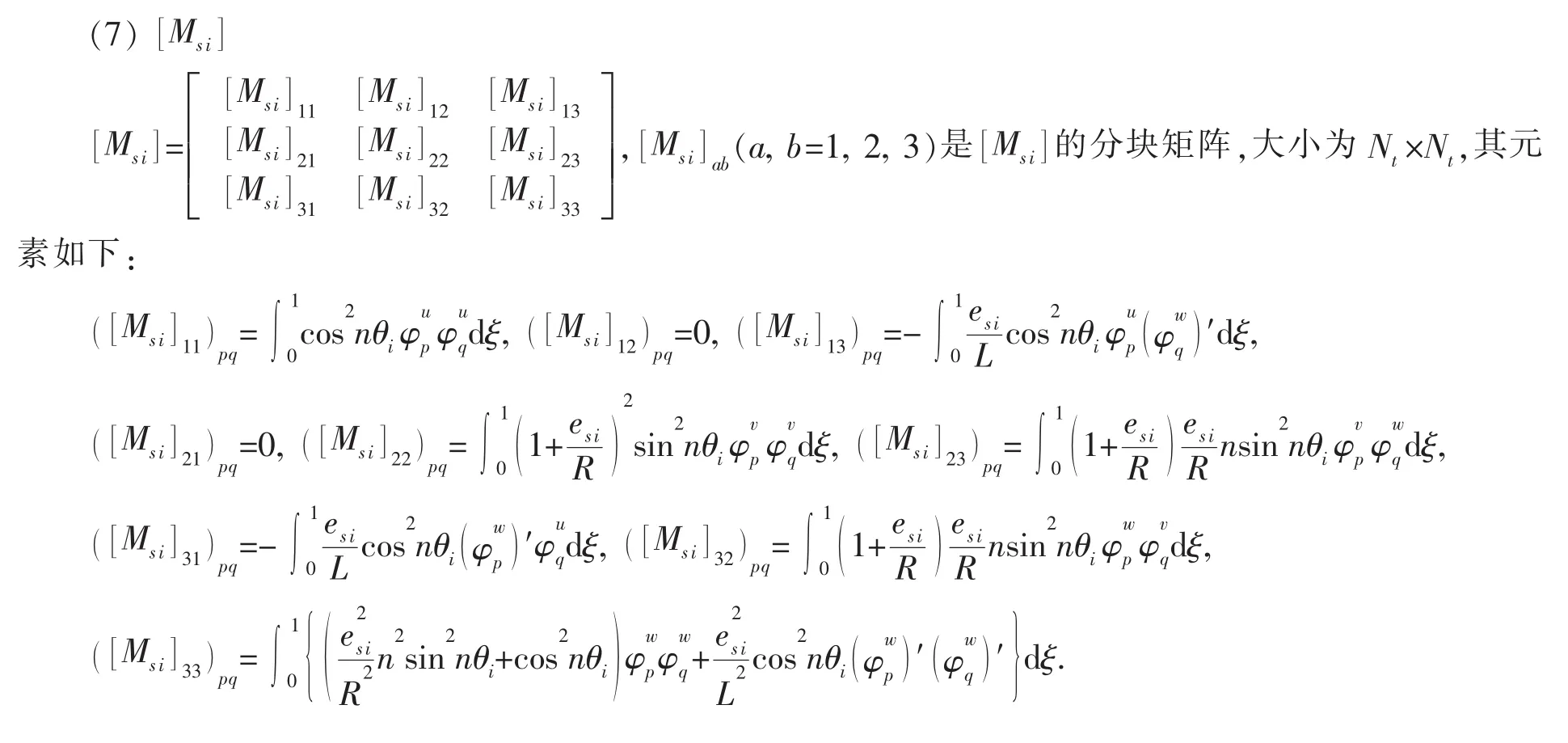
O326
A
10.3969/j.issn.1007-7294.2016.08.011
1007-7294(2016)08-1016-12
2016-02-25
国家自然科学基金项目(90816002)
刘 伦(1990-),男,硕士研究生,E-mail:lnhgdht@sina.com;曹登庆(1958-),男,教授,博士生导师,E-mail:dqcao@hit.edu.cn。
