例析两角和差及倍角公式的应用



例析两角和差及倍角公式的应用

◇山东王秀永

两角和差及倍角公式是解决三角函数化简求值问题的重要公式,也是其他三角公式的推导基础,所以在三角函数的学习过程中,必须充分重视．应用其解题时要掌握角的变化以及三角函数名称的变化技巧,把握化简的标准:一次、一角、一函数．同时在求值时,要注意角的范围影响着三角函数值的符号,这也是解题过程中的易错点．

三角函数的化简是三角变换的基础,即通过一系列的变换,化异为同,达到简化运算的目的,其基本原则是: 1)三角函数的名称及角的种类要尽量的少; 2)三角函数的次数要尽量的低; 3)分母中尽量不含三角函数; 4)能求值的要求出具体值．

常见题型有如下3类．

1等式证明

tan(α-β)+4tanβ=0.

证明由5sinα=3sin(α-2β)可以得到

5sin [(α-β)+β]=3sin [(α-β)-β],

即

5sin(α-β)cosβ+5cos(α-β)sinβ=

3sin(α-β)cosβ-3cos(α-β)sinβ.

得2sin(α-β)cosβ+8cos(α-β)sinβ=0.

①

根据题意得α≠kπ+π/2且

α-β≠kπ+π/2,k∈Z.

式①两边都除以2cosβcos(α-β)得

tan(α-β)+4tanβ=0.

2化简求值

sin(-50°)/(sin50°cos60°)=-2.

解法2原式可化为

2sin(-50°)/sin50°=-2.

sin 2θ-2cos2θ=2sinθcosθ-2cos2θ=

解法2sin 2θ-2cos2θ=sin 2θ-cos 2θ-1=

-cos (2θ+π/2)-sin(2θ+π/2)-1=

3恒等变换

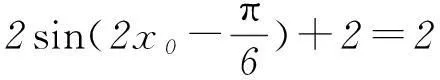
总之,三角函数化简和求值的难点在于多个三角公式的灵活运用,需要认真分析式子的整体结构及角的关系,才能准确找到解题的思维起点．

(作者单位：山东省寿光现代中学)