浅谈高中数学例题解析



浅谈高中数学例题解析

◇甘肃刘克庭

当前,我国正在推广新课程的改革,不但包含了改革课程的内容设立,还包括了改革教师的教学观念、教学方式,只有这样才有助于完成我国的教育体度改革的最终目的．教学中例题教学方式的选择在提升高中数学课堂教学质量、完成教学目的方面发挥了关键的作用．鉴于此,本文拟对高中数学例题解析进行分析与探究．

1例题解析存在的问题

高中数学课程在内容设立层面是相对落后,同时在例题的选取上相对单一，例题的数量比重较大,导致课堂教学目的不容易完成．因为高中数学公式、定理的应用方法通常有很多种,若逐一讲解,就会滞后课程的进程,进而无法实现预期目的．

教师讲解例题时耗费的时间太多,同时讲解得过分详细了,阻碍了学生自主学习与自主探究能力的提升．在整个教学过程中教师忽视了学生的主体位置,只是自己在一味地解说,学生没有考虑与综合的机会,这样会显著地降低高中数学课堂的教学效率,阻碍完成教学改革的目的．在这类情况之下,学生的积极性会被慢慢地打消,长期下去学生就会失去自主学习与单独思考的能力,在自己单独解决题目的时候效率就会显著下降．

2例题解析的注重点

2.1教学方式灵活变通培育学生的思维习惯

著名数学家费赖登塔尔曾经说过：“学习数学唯一科学的方式就是‘再创造’，也就是通过学生本人将要学的东西去发现与创造出来,而教师的重要任务是去指引与协助学生去完成这个再创造性工作，而不是将现有的知识传输给学生．”所以教师在讲解例题时，不要局限于某一类的教学方式与解题思维，更不必把思考经过直接告诉学生,而是要从不同角度去思索例题的解法,从而开阔学生的解题思路．这就需要教师在讲解例题的时候,正确应用小组协作、自探互教等教学方法鼓舞学生自主地去找到新思路、找到新解法，进而培育学生正确的思维方式．另外还需要培育学生反思例题的习惯，利用在例题的思考中完成反思识别解题思路是否严谨、解题方法的多样性,并且尝试总结处理这类问题的普遍规律．

2.2重视思维指引，正确讲解例题

在课堂教学中，应利用教师与学生、学生与学生的互动与协作，按照教学规律正确地把例题探究的思考经过说明白、讲彻底，让学生知道数学思维形成的经过．高效率的数学学习不但需要借助效仿跟记忆,还要指引学生自觉参加到观察、思索、推断、验证与沟通等思维行为中，帮助学生构成自己对数学知识的认知与了解.教师的首要工作就是教会学生去探究、处理问题的想法与方式．

2.3深层探究教材，开发例题的潜在意义

我国著名教育学家叶圣陶先生曾说过：“教材只能作为教课的依据.要使学生真正受到实益主要依据老师在课堂上的运用能力．”教师要深层次地探究所教的知识与所选用例题相互的关联并设定相应的情境，挖掘例题潜在的德育价值，使得学生能够进入到良好的数学情感与人文关怀之中.这不仅能够培育学生对数学学科的感情，还可以潜移默化地改变学生的价值观念．

2.4注重学生能力的扩展

数学例题教学不仅需要学生了解数学的基本知识与技能，其更多的是需要利用例题教学扩展学生的能力.一题多变可以激起学生浓厚的求知渴望，增加学生对课堂所学内容的深刻认识.

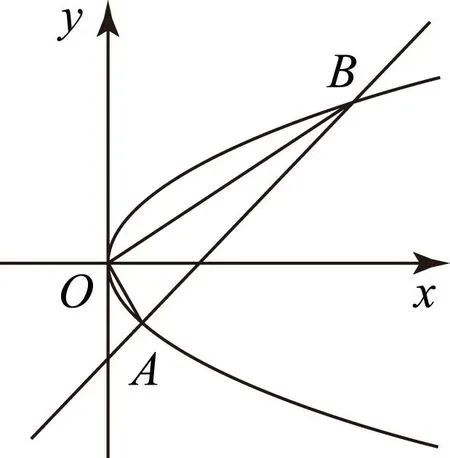
图1

在此题基础上可引导学生进行如下探究:

1) 逆向探究:设点A和B为抛物线y2=2x上原点以外的2个动点,已知OA⊥OB,则直线AB恒过定点Q(2,0).

2) 推广一般:直线AB过Q(2p,0),交抛物线y2=2px(p>0)于A、B,O是坐标原点,则OA⊥OB.

3) 逆向推广:设点A和B为抛物线y2=2px(p>0)上原点以外的2个动点,已知OA⊥OB,则直线AB恒过Q(2p,0).

3例题解析的实例探讨

通过老师的正确指引后，学生自己思考,给出了如下多种变式.

变式1:A={x|x<1},B={x|x≤m},A⊆B,求m的取值范围．

变式2:A={x|x<1},B={x|x>m},A⊆RB,求m的取值范围．

变式3:A={x|-1

变式4:A={x|-1

变式5:A={x|-1

其中变式1与2本质是一样的．变式3与前2题相比，难度增加了.变式4与变式3不同之处是这里的B可以为∅,而在变式5里,能够判断出B不可能是∅．通过这5道变式的训练，不仅可以让学生加强了解集合的包含关联,还可以加深解题的想法.通过分析子集是空集的状况,培育了学生思考的严谨性.

在教师的指引下，学生通过自己思考,给出了多种解法:

思考1如果将x+y看成是一个变量,问题就变成想办法去掉xy项．

思考2利用构建方程来进行处理.

解法2令t=x+y>0,所以y=t-x,代入条件可得x2-tx+2-t=0.由Δ=t2-4(2-t)≥0,解得

思考3条件等式能够完成因式分解,应用积为定值,和有最小值来求解．

解法3由x+y+xy=2可知

(x+1)(y+1)=3,

总之，例题教学是一项较为系统的工作,不能一蹴而就,需要从多方面完善,灵活变通教学方法，进而培育学生的思维方式．

(作者单位：甘肃省景泰县第五中学)