一解多题，培养学生思维品质



一解多题，培养学生思维品质

■常小平1贺永宏2

培养学生数学思维能力的方法有很多，心理学家认为，培养学生的数学思维品质是培养和发展数学思维能力的突破口，数学思维品质包含思维的广阔性、深刻性、独立性、批判性、逻辑性、创造性、灵活性、敏捷性、收敛性及发散性。培养学生思维品质的途径也很多，通过一题多解能培养学生思维的广阔性、深刻性、灵活性，也可通过一解多题培养学生思维的深刻性、创造性、收敛性，增进学生思维的逻辑性，使学生觉得在解数学题时有规律可循，也能提高学生学习数学的信心。下面笔者通过两个看似不同的2015年高考数学题及变形，寻找其本质的共同点，用同一种方法进行解答。

陕西师范大学《中学数学教学参考》(下)2014年第3期上发表了《圆锥曲线的“伴随”点与2013年陕西高考数学题》(作者常小平,下称文1)，文章中记录了作者在解决直线与圆锥曲线问题时发现的一个美妙性质：点与点如影随形地相伴着，故命名为“伴随”点，同时给出了“伴随”点的几个性质，并用这些性质非常简单地解决了2013年陕西高考数学第20题第(Ⅱ)问。为了让读者容易理解本文，特将文1中的结论稍加改进，择录如下：

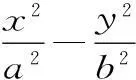
“伴随点”有如下的性质：

(1)互为“伴随点”,即若P′是P的伴随点，则P也是P′的伴随点。

(2)在命题的已知条件下，P′是P的伴随点，当A、B在x轴(或y轴)异侧时，∠AP′B被x轴(或y轴)平分；当A、B在x轴(或y轴)同侧时，∠AP′B的邻补角被x轴(或y轴)平分。

(3)在命题的已知条件下，P′是x轴(或y轴)上的一点，当A、B在x轴(或y轴)异侧，且∠AP′B恒被x轴(y轴)平分(或当A、B在x轴(或y轴)同侧时，∠AP′B的邻补角恒被x轴(或y轴)平分)，则P′是P的伴随点。

2015年高考全国理科卷第20题第(2)问和2015年四川高考理科卷第20题的第(2)问都是“伴随点”的两个变形题，现将它们的解答实录在此，作为一解多题的一个案例。

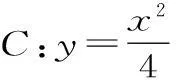
(1)当k=0时，分别求曲线C在点M和N处的切线方程；

(2)在y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由。

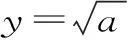
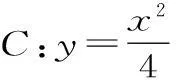
如图1，这样的点存在，为P(0,-a)。

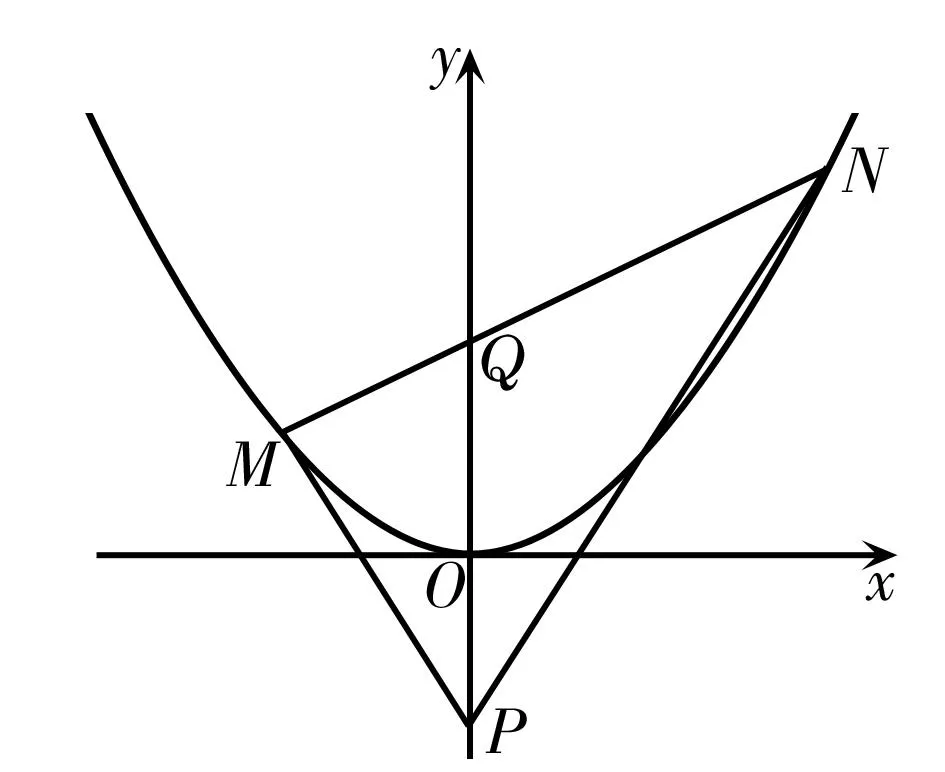
图1

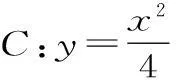
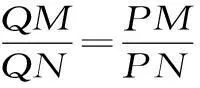
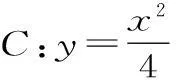
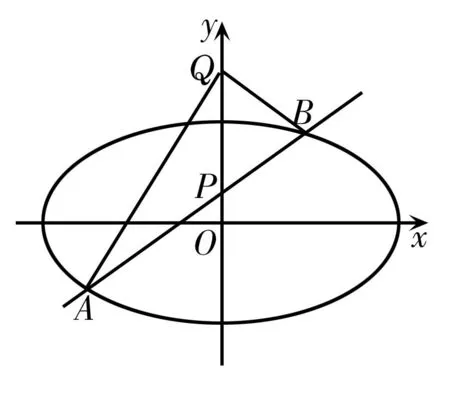
图2

(1)求椭圆E的方程。

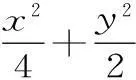
当然我们也可利用QP平分∠AQB，得到直线QA和直线QB的斜率相等，设Q(0,y0)，从而求得y0=2。

变式:在平面直角坐标系xOy中，是否存在与点P不同的点Q，使得∠AQP=∠BQP恒成立？若存在，求出点Q的坐标；若不存在，说明理由。

这两个高考试题的第2问及变式都有一个本质的共同点，就是圆锥曲线的“伴随”点，让学生透过不同的表面现象，抓住问题的本质属性，既培养了学生的思维品质，又使学生学会了分析和研究问题。

参考文献：

1.常小平.圆锥曲线的“伴随点”与2013年陕西高考数学题[J].中学数学教学参考(下)，2014(3).

作者单位：1.陕西省榆林市教研室

2.陕西省榆林市第三中学