如何解决空间几何体表面上的最值问题
2016-04-27张永丰
中学生数理化(高中版.高二数学) 2016年3期
如何解决空间几何体表面上的最值问题
■张永丰
所谓空间几何体表面上的最值问题,是指空间几何体表面上的两点之间的最小距离或某些点到某一个定点的距离之和的最值问题。将空间几何体表面进行展开是化解该难点的主要方法,对于多面体可以把各个面按照一定的顺序展开到一个平面上,将旋转体(主要是圆柱、圆锥、圆台)按照某条母线进行侧面展开,这样就把本来不在一个平面上的问题转化为同一个平面上的问题,结合问题的具体情况在平面上求解最值即可。
例题在长方体ABCD-A1B1C1D1中,AB=3,BC=4,CC1=5,则沿着长方体表面从A到C1的最短路线长为____。
点拨:求几何体表面上两点间的最短距离,可以将几何体的侧面展开,利用平面内两点之间线段最短来解答。
解析:在长方体的表面上从A到C1有三种不同的展开图。
(1)将平面ADD1A1绕着A1D1折起,得到的平面图形如图1所示。
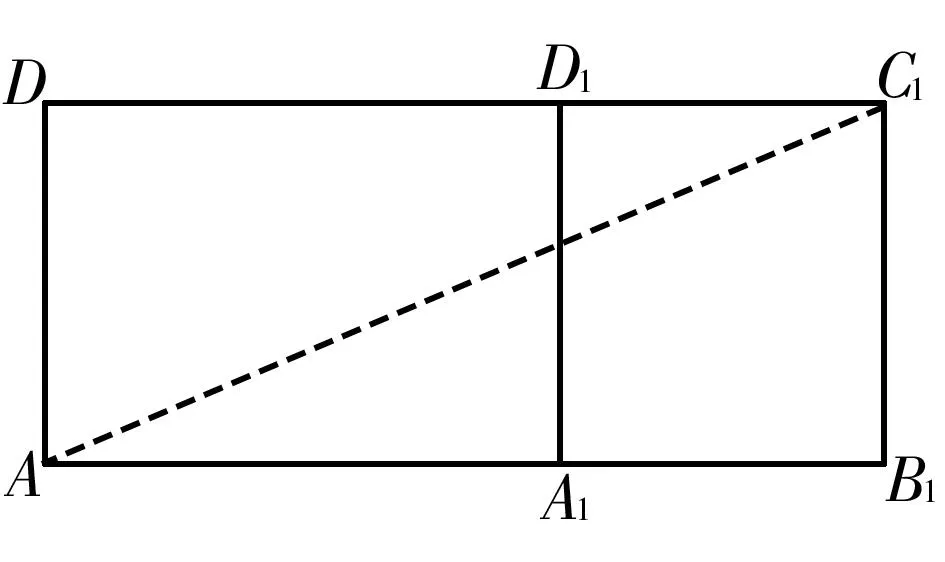
图1
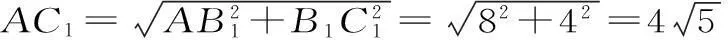
(2)将平面ABB1A1绕着A1B1折起,得到的平面图形如图2所示。
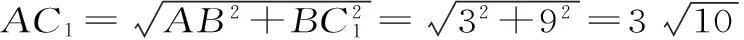
(3)将平面ADD1A1绕着DD1折起,得到的平面图形如图3所示。
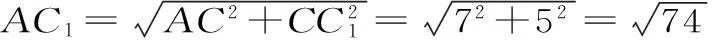
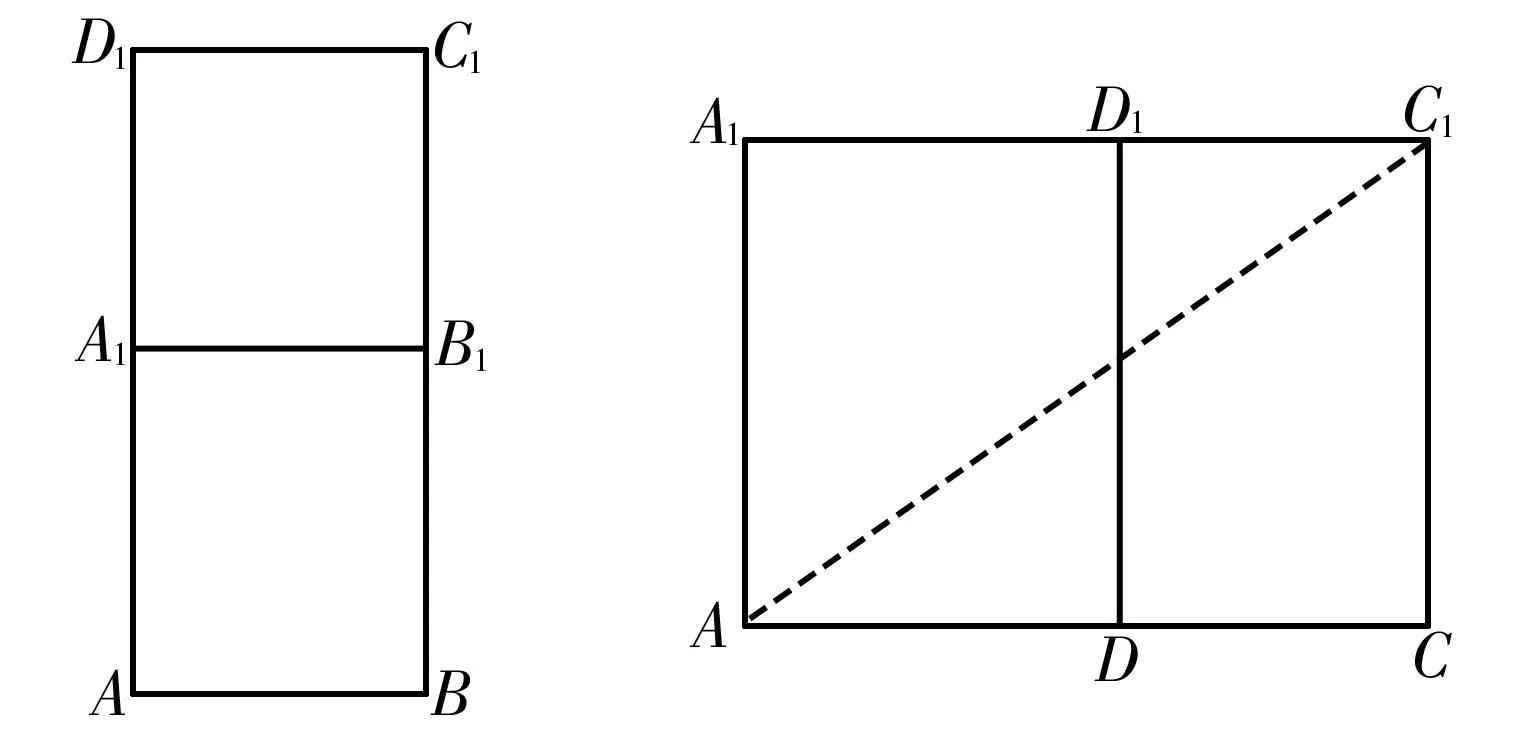
图2 图3
点评:本题的难点在于如何将长方体的表面展开,将其表面上的最短距离转化为平面内两点间的距离来解决。因为长方体的表面展开图形状比较多,其表面展开图因展开的方式不同,会得到不同的结果,应将这些结果再进行比较才能确定最值。本题易出现的问题是只利用一种表面展开图得出数据就误以为是最小值。
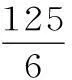
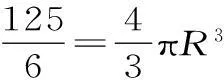
总结:要解决好这类问题,我们同学需要对“空间几何体的结构特征”、“空间几何体的三视图”、“空间几何体的直观图”等知识点非常的熟悉。
作者单位:江苏省泰兴市第一高级中学
