平面近场声全息信噪比估计方法研究

万海波， 朱石坚， 楼京俊， 丁少春

(海军工程大学 动力工程学院，武汉　430033)



平面近场声全息信噪比估计方法研究

万海波， 朱石坚， 楼京俊， 丁少春

(海军工程大学 动力工程学院，武汉430033)

摘要：针对全息面复声压信噪比对声场重构结果影响较大、往往不能直接测量问题，采用二维小波分析方法进行全息面信噪比参数估计，分析小波函数、分解层级对信噪比估计准确性影响，明确二维小波分析的参数选取，并以受简谐激励作用的四周无限大障板简支钢板为对象进行辐射声场全息重构仿真分析。结果表明，信噪比参数对实现准确声场全息重构十分重要，用二维小波分析方法进行全息面信噪比参数估计有效且可行。

关键词：近场声全息；信噪比估计；小波分析；滤波窗

近场声全息[1-2]测试过程中全息面复声压不可避免会引入背景噪声干扰。由于背景噪声分布在整个波数域范围内，逆向重建过程中位于高波数域的背景噪声将会与声源辐射倏逝波成份一起被指数级放大，导致全息重构结果出现较大误差。因此须对全息面复声压进行波数域滤波[3]，其中全息面信噪比作为滤波窗函数重要参数可决定滤波截止波数的选定，严重影响波数域滤波及声场全息重构效果。

而全息面复声压信噪比往往不能直接测得，常用经验判断方法选取，但准确度无法保证。Williams[4]以不发生混迭的最大波数为半径构建辐射圆，取辐射圆外波数域成份近似为全息面复声压噪声信号，计算全息面信噪比，但由于噪声处理区域较实际噪声区域小，估计的信噪比参数往往偏大。在此基础上，辛雨等[5-6]提出以辐射圆外的波数域成份数据均方根值近似代替全息面的噪声信号均方根值，采用能量法及幅值法分别进行信噪比估计，但信噪比估计的准确性严重依赖全息面数据量。

小波分析理论的长足发展为全息面信噪比估计提供了方法，其具有去相关性特点，使噪声信号通过变换后对应大量小的小波系数，而有效信号则往往对应少量较大的小波系数，从而较易区分有效信号与噪声信号，获得全息面复声压信噪比。

因此，本文提出采用二维小波分析方法进行全息面信噪比参数估计。介绍其基本原理，分析小波函数、分解层级对信噪比估计准确性影响，明确二维小波分析的参数选取；并以受简谐激励作用的四周无限大障板的简支钢板为对象，通过仿真分析验证方法的准确性及有效性。

1基本原理

傅里叶分析即将信号分解成不同频率正弦信号的叠加，而小波分析则将信号分解成一系列小波函数的叠加，并由一个母小波函数ψ(x)通过平移及尺度伸缩获得，即

(1)

式中：a为伸缩因子；b为尺度因子；a,b⊂R,且a>0。

对任意f(x)⊂L2(R)，其连续小波变换定义为该函数与小波函数的内积，即

(2)

令a=2-j,b=2-jk，则离散化小波函数为

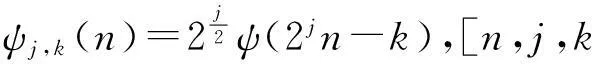
(3)

对离散信号f(n)，其离散小波变换为

(4)

由于全息面复声压P(x,y)本身为二维离散信号，需将一维小波变换扩展到二维，即将二维尺度函数表示成两个一维尺度函数的乘积[7]，即

φ(x,y)=φ(x)φ(y)

(5)

令ψ(x),ψ(y)分别为φ(x),φ(y)对应的一维小波函数，则二维小波函数可表示为3个可分离的正交基函数，即

(6)

二维离散小波变换表示为

(7)

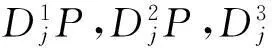
每次分解均使全息面复声压的分辨率变为原来的1/2。全息面复声压二级小波分解过程见图1。

图1　全息面复声压二级小波分解过程Fig.1 The process of the two-level wavelet analysis for the complex pressure

全息面复声压信号经二维小波变换后能使有效信号在小波域集中于少量大的小波系数中，即大尺度低分辨率部分，而噪声分布在整个小波域对应大量小的小波系数，即各尺度高分辨率部分。保留大尺度低分辨率的全部系数，对各尺度高分辨率的小波系数通过设定阈值，幅值低于该阈值的小波系数全部置零，高的或完整保留或收缩处理，并将所得小波系数利用小波逆变换进行重构，恢复有效的全息面声压信号，从而获得全息面声压信号信噪比。此即为二维小波分析实现全息面复声压信噪比估计原理，基本步骤见图2。

图2　全息面信噪比估计流程Fig.2 The flowchart of the estimation for the SNR

2二维小波分析参数选取

用二维小波分析对全息面原始声压信号进行分解与有效声压信号重构过程中，考虑硬阈值易产生边缘吉布斯现象，往往采用软阈值函数处理；阈值设定选取规则选Birge-Massart策略的二维小波阈值[8]。此时小波函数、分解层级选择十分重要，直接决定信噪比估计的准确度。选Birge-Massart策略进行二维小波软阈值处理基础上，通过数值仿真分析小波函数及分解层级对信噪比估计准确性影响。其中全息面复声压信号通过点源平面辐射声场获得，全息面复声压中噪声信号选高斯白噪声。

分解层为2级时采用biro4.4、db8、coif5及sym3小波函数对信噪比估计影响见图3。由对比看出，信噪比在10～30 dB范围内，小波函数对50～1 000 Hz内全息面复声压信号信噪比估计均较准确，误差在4 dB以内，且基本不受分析频率影响；信噪比在40 dB时随分析频率增加，用小波函数进行信噪比估计误差有所增加，其中db8小波函数所致误差最小。因此，采用二维小波分析进行全息面信噪比估计过程中建议选db8小波函数。

选db8小波函数，采用1、2、3、4级分解对信噪比估计影响见图4。由对比看出，信噪比在10～ 40 dB范围内，1级分解对50～1 000 Hz内全息面复声压信号信噪比估计最准确，虽分解层级较低，可能出现全息面噪声信号无法完全有效滤除，导致信噪比估计略高，但该误差在2 dB以内，且基本不受分析频率影响；随分解层级提高全息面声压信号中有效声压信号会被过度提取滤除，导致信噪比估计偏低，出现较大误差，且误差随分析频率及信噪比增加而变大。因此采用二维小波分析进行全息面信噪比估计时建议选1级分解。

图3　不同小波函数对信噪比估计影响(N=2)Fig.3 The effects of the wavelet function on the estimation for the complex pressure signal to noise ratio (N=2)

图4　不同分解级数对信噪比估计影响(db8)Fig.4 The effects of the decompose level on the estimation for the complex pressure signal to noise ratio (db8)

3仿真分析

为验证全息面信噪比参数的重要性及二维小波分析进行信噪比估计的准确性，以受简谐激励作用的四周无限大障板的简支钢板为对象进行辐射声场全息重构仿真分析。令简支板中心为原点建立坐标系，简支板长、宽均为0.5 m，厚0.005 m，杨氏模量2×1011Pa，泊松比0.28，密度7.8×103kg/m3；激励力作用点在(0.2 m，0.2 m)处，幅值1 N，频率858 Hz。此时简支板主要以第(3,3)阶模态振动为主(模态频率857 Hz)。辐射声场空间媒质为空气，取声速343 m/s。

声场计算中全息面大小尺寸为1 m×1 m，测量点数50×50，全息测量面距简支板表面0.05 m，重建面为平板表面。全息面及重建面复声压理论值据瑞利积分获得[9]，其中全息面复声压在理论计算基础上添加高斯白噪声，信噪比30 dB。全息重构过程中滤波窗选带约束的最小二乘滤波窗[10]。

不同信噪比参数下重构结果对比见图5。由图5看出，滤波窗信噪比参数输入20 dB时高波数域内噪声信号及简支板辐射声场有效声压信号均得到衰减，使重构面声压全息计算幅值较理论幅值降低约25%；滤波窗信噪比参数输入40 dB时高波数域内噪声信号未得到充分滤除，使重构面声压全息计算幅值大于理论幅值，且重构面边缘出现一定程度的吉布斯效应；采用二维小波分析全息面信噪比估计后所得滤波窗信噪比参数为32 dB，且重构面声压全息计算幅值与理论幅值误差最小，声场重构效果最好。因此，信噪比参数对实现准确声场全息重构至关重要，而采用二维小波分析方法进行全息面信噪比参数估计行之有效。

图5　不同信噪比参数下重构结果对比Fig.5 The comparison of the sound field reconstruction results in different complex pressure signal to noise ratio

4结论

(1)采用二维小波分析方法进行全息面信噪比参数估计，分析小波函数、分解层级对信噪比估计准确性的影响，明确二维小波分析参数选取。

(2)通过算例进行辐射声场全息重构的仿真分析表明，信噪比参数对实现准确声场全息重构十分重要，采用二维小波分析方法进行全息面信噪比参数估计有效可行。

参 考 文 献

[1] 王冉,陈进,董广明．基于改进HELS方法的局部近场声全息技术研究[J]．振动与冲击,2014,33(10): 157-161．

WANG Ran，CHEN Jin，DONG Guang-ming． Patch near-field acoustic holography based on modified Helmholtz equation least square method[J]．Journal of Vibration and Shock,2014,33(10):157-161．

[2] 张海滨,蒋伟康,万泉．压缩机噪声的跟踪采样近场声全息实验研究[J]．振动与冲击,2010,29(11)：51-54．

ZHANG Hai-bin，JIANG Wei-kang，WAN Quan. Acoustic field test of a rolling-piston compressor using nearfield acoustic holography combined with track-sampling[J]．Journal of Vibration and Shock,2010,29(11): 51-54．

[3] Nam K U, Kim Y H．Errors due to sensor and position mismatch in planar acoustic holography [J]. Journal of the Acoustical Society of America,1999,106(4): 1655-1665．

[4] Williams E G．Regularization methods for near-field acoustical holography [J]. Journal of the Acoustical Society of America,2001,110(4):1976-1988．

[5] 辛雨,张永斌,毕传兴,等．基于空间傅里叶变换的平面近场声全息中信噪比估计方法研究[J]．计量学报，2010,31(6):537-542．

XIN Yu，ZHANG Yong-bin，BI Chuan-xing，et al. Analysis and characterization of line edge roughness of nanostructures[J]．ACTA Metrologica Sinica,2010,31(6)：537-542．

[6] 陈心昭,毕传兴．近场声全息技术及其应用[M]．北京：科学出版社,2013．

[7] 程正兴．小波分析与应用实例[M]．西安:西安交通大学出版社,2006．

[8] 张德丰．Matlab小波分析[M]．北京:机械工业出版社，2009．

[9] Williams E G, Maynard J D．Numerical evaluation of the rayleigh integral for planar radiators using the FFT [J]. Journal of the Acoustical Society of America,1982,72(6): 2020-2030．

[10] 张德俊．近场声全息对振动体及其辐射场的成像[J]．物理学进展,1996,16(3/4):614-623.

ZHANG De-jun．Imaging for vibration mode and radiation field of vibrating object using NAH [J]. Progress in Physics,1996, 16(3/4):614-623.

Estimation of the signal to noise ratio in planar acoustical holography

WANHai-bo,ZHUShi-jian,LOUJing-jun,DINGShao-chun

(College of Power Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract:The complex signal to noise ratio of pressure on an acoustic holography surface has a great influence on the precision of reconstruction results, however it cannot be measured directly. To solve this problem, the method of two-dimension wavelet analysis was proposed, and the effects of wavelet function and decomposition level were analyzed, which will help the decision making for parameters selection in the two-dimension wavelet analysis. The proposed method was validated by suing the synthetic sound field created by a point-driven, simply supported plate. The result show that the two-dimension wavelet analysis used to estimate the complex signal to noise ratio of pressure is feasible.

Key words:acoustic holography; signal to noise ratio estimation; wavelet analysis; filter window

中图分类号:O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.017

通信作者朱石坚 男，教授，博士生导师，1955年生

收稿日期：2015-01-06修改稿收到日期：2015-03-12

基金项目：高等学校全国优秀博士学位论文作者专项资金(201057)

第一作者 万海波 男，博士生，1987年生