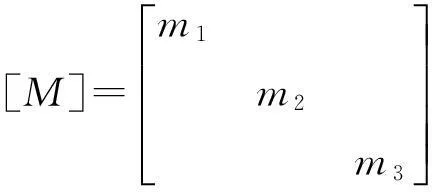改进的受力状态映射法在结合部动力学参数辨识中应用

李金峰， 王立平

(清华大学 机械工程系，北京　100084)



改进的受力状态映射法在结合部动力学参数辨识中应用

李金峰， 王立平

(清华大学 机械工程系，北京100084)

摘要：针对受力状态映射法作为辨识非线性结合部参数重要方法具有物理意义明确、辨识准确等特点，而实际辨识试验时结构某些参数难以测定、致辨识过程困难等问题，提出结合子结构模态综合法的受力状态映射法，可有效解决该问题。参数辨识过程中对模型易出现的缺失项及冗余项，利用基于TSVD(Truncated Singular Value Decomposition)正则化方法的模型迭代修正法。仿真模型表明，修正模型较精确模型误差小、辨识精度高。通过对导轨结合部进行参数辨识实验研究，证明辨识方法的有效性及准确性。

关键词：非线性结合部；参数辨识；受力状态映射法；TSVD正则化

结合部动态特性对机床影响较大，欲准确分析整机动态特性，不仅获取零件、部件及组件的动力学参数，且需获取其结合部的动力学参数方能建立整体动力学模型进行分析。而单纯靠试验或有限元法不可能精确获得结合部动力学参数，须通过一定辨识方法对参数进行辨识。结合部动力学参数通常包括动刚度、阻尼等，且常表现出非线性。因而寻找精确、合适的结合部非线性参数辨识方法获取准确动力学参数、构建整机动力学模型为整机动力学、动态特性分析及结构优化设计的先决条件。受力状态映射法由Crawley等[1]提出，即将结合部间的力视为外力，并与状态之间建立映射关系。该法物理意义直观，表达方式明确，且较频响函数法等传统辨识方法可辨识出结合部间除刚度、阻尼外的其它非线性联接关系。

鉴于结合部非线性参数难以识别特点，对该方法已进行一系列改进。Kim等[2]在频域利用受力状态映射法对非线性结合部参数辨识表明，辨识精度较高。其虽对所建模型与假设模型相同情况进行分析，但未对假设模型为其它情况时如何辨识进行深入研究。Shin等[3]提出由延拓算法与力映射法构成的伪力状态映射法。针对受力状态映射到响应信号相位滞后问题，Meskell等[4]提出评估敏感性参数估计方法。Wang等[5]证明不确定结合部模型下在频域仅靠离散数据不能获得完备的受力状态。蔡力钢等[6]在受力状态映射法基础上用Tikhonov 正则化与迭代算法结合对结合部等效力矢量模型进行更新，辨识出结合部等效动力学参数。Jalali等[7]将受力状态映射法用于单个螺栓结合部参数辨识，获得立方刚度及黏性阻尼。Dhupia等[8-9]提出通过非线性恢复力计算滚动导轨结合部阻尼方法，非线性恢复力具体形式用二维切比雪夫多项式表述。通过对试验结果最小二乘估计获得该非线性恢复力表达式系数，进而求出结合部阻尼。

实际辨识试验中由于某些结合部整体结构难以拆分，且结合部处形状不规则，导致子结构频响函数难以测定；某些结合部变形极小，甚至在微米级以下，导致测量困难。对此，本文提出结合子结构模态综合法的受力状态映射法，经改进后能有效解决此问题。即在参数辨识中用基于TSVD正则化方法的模型迭代修正法，通过仿真证明该方法能有效发现模型中缺失项及冗余项，辨识精度较高，并用该方法对导轨结合部动力学参数进行辨识。

1受力状态映射法

用受力状态映射法进行参数辨识前，需对各子结构及结合部进行假设，即①各子结构为线性，结合部为非线性，整个结构可划分为若干线性子结构及非线性结合部；②各子结构频响函数矩阵可通过仿真或实验获得。

1.1动力学方程建立

线性子结构1、2通过m个非线性结合部连接，见图1。忽略结合部质量时其特性可由一系列非线性弹簧及阻尼表示。图2中整个结构由结合部处分离，通过结合部传递力视为子结构1、2所受外力。子结构1中区域a代表结合部区域，p代表除结合部区域外的其余区域，同理子结构2中区域b代表结合部区域，q代表除结合部区域外的其余区域。

图1　一般非线性结合部模型Fig.1 General nonlinear joint model

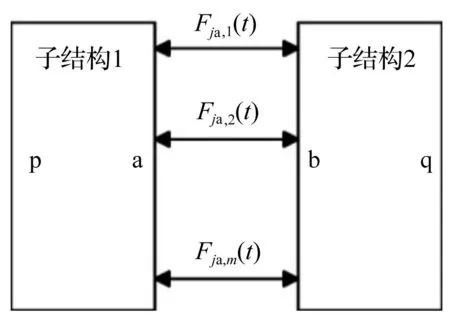
图2　非线性结合部等效模型Fig.2 Nonlinear joint equivalent model

由于子结构1、2所受结合部力大小相等、方向相反，因此只需分析其中之一即可。线性子结构1的动力学方程为

[K1]{x1(t)}={f1(t)}+{fj(t)}1

(1)

式中：[M1]，[C1]，[K1]为子结构1的质量、阻尼及刚度矩阵；{x1(t)}为位移矢量；{f1(t)}为作用于1的外力矢量；{fj(t)}1为作用于1的结合部力矢量。

将子结构1按结合部及非结合部区域分解，并将1的动力学方程变到频域，则式(1)可写为

取式(2)第二行，得

[Haa]{Fja(ω)}={X1a(ω)}-

[Hap]{F1p(ω)}-[Haa]{F1a(ω)}

(3)

式中：[Haa]，[Hap]为子结构1在 a区域频响函数； {F1p(ω)}，{F1a(ω)}为作用于区域p及a的激振力；{X1a(ω)}为区域a处位移矢量；{Fja(ω)}为区域a处结合部力矢量。

频响函数[Haa]，[Hap]可通过实验或有限元法测定。整个结构受任意点外部简谐激振力时结合部位移响应{X1a(ω)}、激振力矢量{F1p(ω)}及{F1a(ω)}可测定；可由式(3)辨识获得结合部力矢量{Fja(ω)}。

1.2结合部力模型

结合部力模型由结合部受力状态决定。设受力模型为关于结合部相对位移、速度的多项式函数。结合部力模型未知时其力矢量{fja(t)}中第i个结合部力可据受力状态表示为

(4)

结合部力矢量{fja(t)}共(nsi+1)×(nri+1)-1个等效分力，则式(4)可写为

(5)

结合部有m个结合部力时进行傅里叶变换，得

{Fjp(ω)}=

至此，结合部力模型已建立完成，结合部受力状态可映射到表征结合部力模型的动力学参数。若结合部受力状态已知，便可辨识出其动力学参数。

2改进的受力状态映射法

2.1子结构模态综合法

子结构法作为动力分析、动态响应计算不可或缺的分析工具，能充分利用各子系统动态特性，通过便捷计算或实验获取子结构模态特性，进而获得可靠的整体系统动力学特性参数或动态响应。

在子结构模态综合法中所用子结构主要有模态子结构与连接子结构两类。前者指进行模态分析并保留若干低阶主模态参与系统近似坐标变换，进行子结构模态分析时为独立子系统；后者则为特殊子结构，其自由度与相邻模态子结构共有，对其不进行主模态分析、不建立单独模态变换。利用该特性可将子结构模态综合法用于非线性动力学系统参数辨识。

与线性系统类似，对非线性系统实施模态综合法，包括①分解：即将整体结构解体为一系列独立子结构；②分析：各子结构均为线性子系统，可由有限元法或试验获得其自由界面主模态且保留低阶模态；③总装：经模态分析获得各子结构模态信息后各子结构运动可用一组缩减的低阶主模态代表，集合各子结构运动方程即可获得系统运动方程，子结构间连接通过非线性力实现。

2.2辨识方程建立

设结合部连接为弱连接，忽略子结构剩余附着模态对计算精度影响，则子结构1的保留主模态为

[Φ1]=[φ1,1,φ1,2,…,φ1,x1]

(7)

[Λi]=diag[Λi,1,Λi,2,…,Λi,xi]

(8)

式中：[Φ1]，[Λ1]为子结构1的模态及特征值矩阵。

子结构坐标变换的近似关系为

{x1}=[Φ1]{η1}

(9)

经坐标变换，得

[K1][Φ1]{η1(t)}={F1(t)}+{fj}

(10)

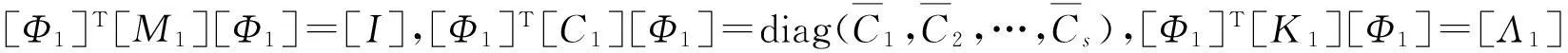
式(10)可表示为

[Φ1]T{F1(t)}+[Φ1]T{fj(t)}1

(11)

装配所有子结构方程，得整个系统方程为

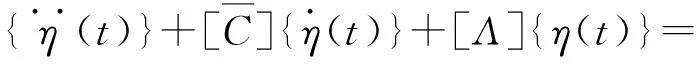
[Φ]T{F(t)}+[Φ]T{fj(t)}1

(12)

系统模态主坐标向量及模态矩阵为

{η(t)}=col[η1(t),η2(t),…,ηs(t)]

[Φ]=diag(Φ1,Φ2,…,Φs)

特征值及块对角阻尼矩阵为

[Λ]=diag(Λ1,Λ2,…,Λs)

令{Q(t)}=[Φ]T{F(t)}称为模态激振力，将阻尼力并入非线性力，式(12)可转化为

由傅里叶变换，得

[Φ]T{fj(ω)}1=[Λ]{η(ω)}+

(13)

3参数辨识

对式(13)展开辨识，其中模态矩阵[Φ]可写为

(14)

将{fj(ω)}1简写为{F(ω)}，将式(6)、(14)代入式(13)，并令方程右边为{μ(ω)}，则有

[Φ]{F(ω)}={μ(ω)}

(15)

[HG(ω)]{λ}={μ(ω)}

(16)

式中：

{HG(ω)}=

当N个不同激振频率的激振力分别作用于系统时，式(16)可表示为

(17)

式(17)可简写为

(18)

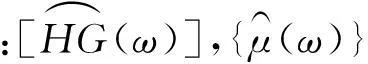
将式(18)分解为实部与虚部，即

(19)

式(19)可简写为

[A]{λ}={B}

(20)

矩阵[A]的行数不小于列数时矢量{λ}可通过最小二乘法求得，即

{λ}=[A]+{B}

(21)

式中：[A]+=([A]T[A])-1[A]T为[A]的广义逆矩阵。

不考虑外部噪声干扰时，可设所建结合部力矢量模型与实际模型一致，只需获取矩阵[A]及矢量{B}中必要参数，即可通过最小二乘法辨识出矢量{λ}。

而实际辨识中结合部等效力矢量未知。若假设模型不含所有精确项而多了不应存在的冗余项，加之外部噪声干扰，则通过最小二乘法求解误差较大，其解会出现病态性。因此本文用基于TSVD正则化模型修正迭代法，对此类情况进行研究。

3.1TSVD正则化方法

TSVD正则化方法又称截断奇异值分解正则化方法。据奇异值分解定理，矩阵[A]的SVD分解表示为

(22)

式中：[U]=(u1,u2,…,um),[V]=(v1,v2,…,vn)为正交矩阵;

设式(20)中矩阵[A]及矢量{B}均受噪声影响，引入扰动矩阵为

([A]+[δA]){λ}=({B}+{δB})

(23)

简写为

[An]{λ}={Bn}

(24)

因此，式(21)可表示为

{λ}=[An]+{Bn}=([An]T[An])-1[An]T{Bn}=

(([U][S][V]T)T([U][S][V]T))-1×

([U][S][V]T)T{Bn}=

(25)

若δi接近0，则{Bn}的误差会被放大。而TSVD正则化方法可较好解决此问题。在TSVD正则化方法中式(25)右端被截断,即前k阶较大奇异值被保留，剩余(r-k)阶较小奇异值被舍弃，因而可避免误差放大，增加解算的稳定性。优化参数k可据奇异值大小确定。

设[Dk]=diag(δ1,δ2,…δk)且k

(26)

因此，式(25)可写为

(27)

3.2模型迭代修正法

考虑噪声影响时结合部动力学参数由式(24)辨识获得，矩阵[An]行数不小于列数时受噪声影响，等式不成立，可通过模型修正迭代法使等式两边误差减至最小。若设结合部力矢量模型不含所有精确项，则误差不可控，迭代会发散；而假设结合部力矢量模型含所有精确项，误差会显著减小。因此，为检验假设模型是否含所有精确项，定义收敛标准为

(28)

式中：{λn}为通过TSVD正则化方法辨识参数；ξ为残差率，越趋近于0说明收敛效果越好，模型中含精确项越多辨识精度越高。

TSVD正则化方法可有效减小外部噪声的影响，模型可据收敛标准进行修正，因此将两者结合，获得模型迭代修正法，有效修正假设模型，并使其不断包含实际模型中精确项，排除所有冗余项干扰。具体流程为：

(1)根据式(4)建立结合部假设模型，任意设定相对速度及位移幂次；

(2)通过TSVD正则化法辨识模型动力学参数；

(3)由式(28)计算残差率，若结果足够好则可认为假设模型已含所有精确项，若结果不好则表明精确项缺失，需增大相对速度及位移幂次，重复步骤(2)，直到残差率在接受范围内；

(4)假设模型中含所有精确项后检查是否含冗余项。计算结合部力中每项分力的比重，即

(r=0…nri,s=0…nsi)

(29)

(5)通过TSVD正则化方法辨识模型动力学参数；

(6)通过式(28)计算残差率，若结果仍足够好，则可认为上一步中剔除的为冗余项，重复步骤(4)；若残差率变大，说明上步中剔除的为精确项，需保留之前的那一项，剔除此项之外比重最小项。重复步骤(5)；

(7)剩余的每项均不会使残差率变低时迭代停止，此时认为每项均为实际模型中的精确项。

4数值仿真

为验证辨识方法的有效性、准确性，用三自由度非线性受迫振动系统对非线性结合部动力学参数进行辨识。如图3所示，设质量块m2与m3间为非线性连接，其余均线性连接，除非线性连接外的系统参数见表1。

图3　三自由度系统Fig.3 A three DOF system

m1/kgm2/kgm3/kgk1/(N·m-1)k2/(N·m-1)c1/(N·s·m-1)c2/(N·s·m-1)1119×1069×10666

设整个系统模态、特征值矩阵可通过计算或试验获得，整个结构受某一固定激振频率的外部激振时，系统稳态响应可通过MATLAB计算求得，常微分方程求解可用MATLAB的求解器“ode23t”求解。便可通过式(13)辨识获得结合部力矢量。

由于假设模型与精确模型相同、无噪声影响时，辨识的参数会非常精确，此处不赘述。为说明本文所用辨识方法，分两种情况进行研究。

4.1情况1

设所建模型含所有精确项，并含冗余项。已知的非线性结合部精确模型可表示为

(30)

式中：λ10=9×107；λ01=4；λ20=3×105。

据给出的精确受力模型可求得整个结构固有频率。建立系统线性齐次无阻尼方程为

(31)

式中：

求解系统固有频率及特征值矩阵。系统三阶固有频率分别为222.5 Hz、714.9 Hz、2 164 Hz。将激振频率选在第二阶固有频率附近进行计算，即711 Hz, 712 Hz,…,720 Hz；外界激振力记为f2(t)=1 000sin(2πft)；结合部位移矢量由常微分方程求出时域曲线，通过傅里叶变换到频域；采样频率为最高激振频率的2倍以上。仿真时分别添加5%、10%的随机噪声。

由于结合部力模型未知，据式(4)，令r=2,s=1，则假设的力模型可表示为

(32)

对fja(t)进行傅里叶变换，用参数辨识方法进行辨识，结果见表2。由表2看出，辨识精度较高，分力比重较大项的相对误差较小，分力比重较小项受误差影响较大。在迭代过程中冗余项不断被剔除，直至模型含所有精确项。

表2　结合部参数辨识结果

4.2情况2

设所建模型未含所有精确项，并含冗余项。假设已知非线性结合部的精确模型及激振频率、激振力同情况1，结合部参数辨识结果见表3。力模型可表示为

表3　结合部参数辨识结果

由表3看出，辨识精度仍较精确，证明在模型迭代更新过程中所有精确项已在模型中，再按情况1步骤剔除冗余项即可。由此该辨识方法对含精确项及冗余项模型亦适用。

5导轨结合部参数辨识实验研究

以真实实验系统为研究对象，利用本文辨识方法进行滚动导轨结合部的动力学参数辨识。搭建可用于多种导轨结合部参数辨识实验台，通过力传感器及加速度传感器实现激振力、加速度高频采集功能，并通过工控机、数据采集软件实时获得激振力及加速度时域曲线。实验台主要由机械结构部分、激振器系统及数据采集系统组成，见图4、图5。

机械结构主要包括导轨、导轨基座、滑座及小型折叠式液压吊车等。激振器系统包括激振器、信号发生器、功率放大器、激振杆及冷风机等。数据采集采用北京东方振动与噪声研究所的DASP V10系统，包括工控机、力传感器、加速度传感器、电荷放大器等，可实现24通道同步采集，每通道最大采样频率102.4 kHz，完全满足实验要求。

图4 数据采集系统图5 机械结构和激振器Fig.4DataacquisitionsystemFig.5Mechanicalstructureandvibrationexciter

5.1参数辨识实验

以THK SHS55导轨为研究对象，实验流程如下：

(1)测定滑块与滑座固定后固有频率。滑座作为滑块与激振杆间连接部件起降低滑块固有频率作用，将滑块、滑座视为整体考虑。对滑块进行模态实验，测得该状态下垂直振动频率，以此频率作为激振频率带中心值。

(2)激振实验。将加速度传感器用磁铁吸附于滑座表面中心，力传感器一端与激振杆相连，另端通过螺钉与滑座固定。调节激振器高度，保持激振杆垂直滑座表面，未发生任何弯曲变形。将传感器与采集仪连接，即可获取激振力及加速度实时信号。

实验以低、中两组不同预压导轨作为对比，每组导轨进行多组激振力实验，激振力大小设定线性增长。激振频率选在垂直振动频率附近；低预压下测定垂直振动频率为1 130 Hz，激振频率带定为(1 126 Hz,1 127 Hz,…, 1 130 Hz, …,1 135 Hz)；中预压下测定垂直固有频率为1 270 Hz，激振频率带定为(1 266 Hz,1 267 Hz,…, 1 270 Hz, …,1 275 Hz)。以中预压导轨加15 N激振力为例，保持激振力幅值在所有激振频率下不变，设采样频率为51.2 kHz，采样时间0.02 s，用信号发生器控制激振频率逐级变化，也可设置逐频扫描。所得该实验不同频率加速度响应曲线，见图6。

图6　加速度时域曲线(1 270 Hz)Fig.6 Acceleration curve in time domain(1 270 Hz)

(3)数据后处理。实际中位移、速度信号不易直接获取，需通过加速度信号积分得到(图6)，若加速度信号起始相位非零点或极点，直接对加速度信号积分所得位移、速度信号会相位失真。动态参数中阻尼系数对积分信号相位失真较敏感，小程度相位失真亦会导致辨识中阻尼系数误差放大。

在单频率谐波激励下，结构响应也是谐波，即使结构存在一定非线性，也能获得高次谐波，便可消除数值积分中位移或速度任何相位失真。因此激振频率等于ω时，加速度信号可利用傅里叶级数展开式表示，即

(34)

将实验获得加速度信号拟合成式(34)形式可获得未知系数An，Bn，进而通过积分获得速度、位移信号表达式，即

Bncos(nωt)]+C1

(35)

Bncos(nωt)]+C1t+C2

(36)

由于速度、加速度信号均值为0，因此C1=C2=0。以加速度信号为例，用MATLAB拟合工具箱进行拟合，所得位移、速度曲线见图7、8。由两图看出，位移数量级在微米以下，若直接测定结合部变形非常困难。

图7　位移时域曲线(1 270 Hz)Fig.7 Displacement curve in time domain (1 270 Hz)

图8　速度时域曲线(1 270 Hz)Fig.8 Velocity curve in time domain (1 270 Hz)

5.2结合部参数辨识计算

导轨结合部力假设模型为多项式形式，其中分项须有物理意义，因此假设

(37)

式中：λ10为线性刚度，λ01为线性阻尼，此两项为线性连接；λ02为平方阻尼，λ30为立方刚度，此两项为非线性连接。

据式(13)，单自由度情况可简化，并变换到频域

(38)

将式(37)变换到频域并代入式(38)，可得最终辨识式，进而获得导轨结合部在中预压、激振力为15 N时结合部力的表达式，即

(39)

由式(39)所得结合部力模型共三项，按各项在总力中比重依次为线性刚度项、线性阻尼项及平方阻尼项。依次进行不同预压、激振力的动态参数辨识，可得导轨结合部在不同工况的动力学参数。

6结论

(1)本文提出的结合子结构模态综合法受力状态映射法，通过将测定频响函数过程改进为测定结构模态参数过程，不仅保留原方法优点，且使实验过程简化易行。

(2)用基于TSVD正则化方法的模型迭代修正法进行辨识模型修正。数值仿真中考虑的含所有精确项与冗余项及未含所有精确项模型，辨识参数与设定参数误差均较小，辨识精度较高。

(3)用改进的受力状态映射法对导轨结合部动力学参数辨识实验，获得非线性力模型。而物理因素及外界条件对结合部动力学参数影响规律及单一或多个影响因素变化的连续辨识方法尚需进一步研究。

参 考 文 献

[1] Crawley E F, O’donnell K J. Force-state mapping identification of nonlinear joints[J].AIAA Journal,1987,25(7):1003-1010.

[2] Kim W J, Park Y S. Nonlinear joint parameter-identification by applying the force-state mapping technique in the frequency-domain[J]. Mechanical Systems and Signal Processing, 1994, 8(5):519-529.

[3] Shin K, Hammond J K. Pseudo force-state mapping method:incorporation of the embedding and force-state mapping methods[J]. Journal of Sound and Vibration, 1998, 211(5): 918-922.

[4] Meskell C, Fitzpatrick J A. Errors in parameter estimates from the force state mapping technique for free response due to phase distortion[J]. Journal of Sound and Vibration, 2002, 252(5): 967-974.

[5] Wang J H, Huang H Y. Problem of uniqueness of non-linear joint parameter identification by force-state mapping without knowing the joint model[C]//ASME International Design Engineering Technical Conference Computers & Information in Engineering Conference.Long Beach, CA, United states, 2005.

[6] 蔡力钢,李玲,郭铁能,等. 基于力状态映射法辨识非线性结合部动态参数 [J]. 机械工程学报, 2011, 47(7): 65-72.

CAI Li-gang, LI Ling, GUO Tie-neng, et al. Identification of nonlinear joint parameters with force-state mapping method[J]. Journal of Mechanical Engineering, 2011, 47(7): 65-72.

[7] Jalali H, Ahmadian H, Mottershead J E. Identification of nonlinear bolted lap-joint parameters by force-state mapping [J]. International Journal of Solids and Structures,2007,44(25/26): 8087-8105.

[8] Dhupia J S, Ulsoy A G, Katz R, et al. Experimental identification of the nonlinear parameters of an industrial translational guide for machine performance evaluation [J]. Journal of Vibration and Control, 2008, 14(5): 645-668.

[9] Dhupia J S, Powalka B, Ulsoy A G, et al. Experimental identification of the nonlinear parameters of an industrial translational guide[C]//Proceeding of 2006 AMSE International Mechanical Engineering Congross & Exposition. Chicago,IL:IMECE,:1089-1097.

Application of an improved force-state mapping method in dynamic parameter identification of joints

LIJin-feng,WANGLi-ping

(Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China)

Abstract:Force-state mapping method is an important method for the parameter identification of nonlinear joints. The method is of attractive features of clear physical meaning and high identification accuracy. However, certain parameters are difficult to measure during actual identification experiments. Aiming at such problem, a force-state mapping method based on substructure modal synthesis method was proposed. Furthermore, an iterative correction method based on the truncated singular value decomposition (TSVD) regularization was proposed to overcome difficulties associated with term-deficiency and term-redundancy, which may occur during the parameter identification process. The simulation results show the high identification accuracy, demonstrated by the small error between corrected and precise models. Finally, the parameter identification of the joints of a rolling guide was carried out experimentally. The experiments verify the effectiveness and correctness of the identification method.

Key words:nonlinear joint; parameter identification; force-state mapping method; TSVD regularization

中图分类号:TH113

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.003

通信作者王立平 男，博士，教授，1966年5月生

收稿日期：2015-02-09修改稿收到日期：2015-03-26

基金项目：国家杰出青年科学基金(51225503)

第一作者 李金峰 男，博士生，1987年2月生

E-mail：lpwang@mail.tsinghua.edu.cn