机电集成压电谐波电机传动系统非线性自由振动分析

李　冲， 许立忠， 高立超

(燕山大学 机械工程学院，河北 秦皇岛　066004)



机电集成压电谐波电机传动系统非线性自由振动分析

李冲， 许立忠， 高立超

(燕山大学 机械工程学院，河北 秦皇岛066004)

摘要：设计集压电驱动、谐波传动及活齿传动为一体的机电集成压电谐波电机，并分析其工作机理。借鉴行星齿轮传动理论，建立传动系统动力学模型。利用Linz Ted-Poincaré法推导传动系统非线性频率特性方程及位移响应方程，分析传动系统的非线性频率变化规律及时域响应特点；通过ANSYS有限元软件对频率进行验证。结果表明，传动系统非线性由啮合齿数变化引起，啮合齿数越少系统非线性越显著；系统位移响应受非线性影响最明显、微弱的分别为波发生器x及u向；利用有限元仿真验证动力学模型的正确性。

关键词：压电谐波电机；传动系统；非线性；自由振动；Linz Ted-Poincaré法

近年来，以形状记忆合金、电致伸缩材料、磁致伸缩材料及压电材料主导的智能材料获得迅速发展，而其中的压电材料成为研究焦点[1]。适应各场合各类微型压电驱动装置层出不穷，Toyama[2]将设计的球形压电超声电机作为相机作动器用于管状探测机器人；Jeong等[3]设计、制造出用于微型移动设备的三足式薄状旋转压电超声电机；赵淳生[4]研发的压电超声电机首次用于“嫦娥三号”探测器，实现月球完美着陆。

传统压电电机主要靠定转子间摩擦传递转矩，存在接触面磨损严重、寿命短等缺点[5]。非接触式压电电机虽避免摩擦，但承载能力较低[6]。压电谐波电机能克服此缺陷，Oliver[7]设计出利用谐波齿轮及压电堆传动、堵转转矩为0.75 Nm的谐波压电电机；辛洪兵等[8]利用位移放大机构设计出压电谐波电机。以上电机均采用谐波齿轮传动方式，因而对柔轮材料的抗疲劳强度、加工等要求较高，且该齿轮存在传动比下限值较高等缺陷[9]。基于此，本文提出既能降低摩擦损耗、增加电机寿命、又能增大电机输出力矩的机电集成压电谐波电机[10]。该电机集压电驱动、活齿传动及谐波传动于一体，通过活齿啮合取代定、转子间摩擦力驱动转子。

活齿传动系统非线性动力学对电机工作性能产生重要影响，目前对活齿系统动力学研究主要集中于摆动活齿建模、固有频率分析及参数振动分析等[11-13]，而对活齿系统非线性振动研究较少。本文对机电集成压电谐波电机传动系统进行非线性动力学建模，对非线性与线性频率关系及位移响应方程进行推导。

1机电集成压电谐波电机工作原理

机电集成压电谐波电机见图1，电机由驱动、传动系统构成，其中驱动系统包括2个压电堆1、2个弹性体2及摆动体3等，传动系统包括波发生器7、中心轮5、活齿架6、30个活齿4等。电机利用位置互成90°方向的两压电堆作驱动源。给两方向压电堆分别接入峰峰值为150 V相位差π/2且带正偏置的余弦信号后，两压电堆产生具有相位差的往复伸缩变形，通过弹性体及摆动体位移的放大作用，波发生器7边缘处形成连续谐波，并产生径向推力推动活齿沿中心轮齿廓滑动，带动活齿架转动，进而使与活齿架固连转轴旋转，输出转矩。

1.压电堆　2. 弹性体　3. 摆动体　4. 活齿　5. 中心轮　6. 活齿架　7. 波发生器　8. 弹簧图1　机电集成压电谐波电机图Fig.1 An electromechanical integrated harmonic piezo-motor

2传动系统动力学模型

传动系统动力学模型见图2，其中图2(a)为活齿与各构件相对位移，图2(b)为系统各构件受力。OXY为定坐标系，oxy为活齿架坐标系，oixiyi为各活齿坐标系(i=1,2,…,Z)，角标s,c,r,p分别代表波发生器、中心轮、活齿架及活齿。xj,yj,uj分别为x,y向线位移及圆周向线位移(j=s,c,r,p1,…,pZ)。

图2　传动系统动力学模型Fig.2 Dynamic model of drive system

由图2(a)知，系统各主构件(波发生器、中心轮、活齿架)相对活齿位移沿啮合线方向投影为

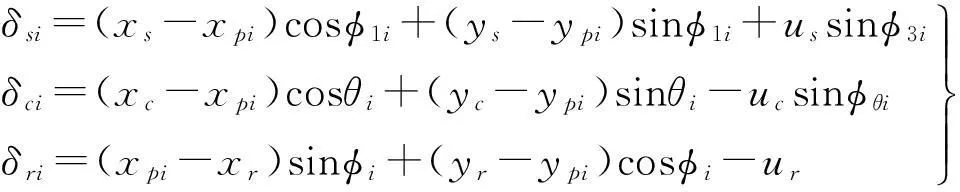
式中：φ1i=φi+φ3i，φθi=φi-θi；θi为各构件因系统振动产生的角位移；φi为第i个活齿中心及活齿架中心连线与固定坐标系X正向夹角；φ3i为波发生器中心与第i个活齿中心连线与第i活齿中心与活齿架中心连线夹角。

活齿系统动力学方程为

(2)

式中：mj，Ij为各构件质量及等效质量，kg；kj，kjz，kjt分别为活齿与各构件啮合刚度、波发生器径向支撑刚度及切向扭转刚度，N/m；rj为各构件理论半径，m；Ts为波发生器转矩，N·m。

3传动系统非线性动力学方程

机电集成压电谐波电机系统输出转矩T随活齿架转角θ变化见图3。每经过π/435则T出现一次突变。图3(b)为一个周期τ=π/435内T随θ变化值，由于T的表达式较复杂且为分段形式，故用多项式拟合，即

T1=τ1θ2+τ2θ+τ3, (0≤θ<π/435)

(3)

式中：τ1～τ3为多项式拟合系数。

为将全部周期转矩T表达成一个方程，对式(3)进行傅里叶展开为

(4)

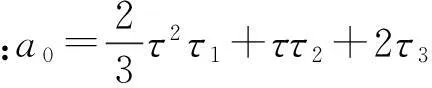
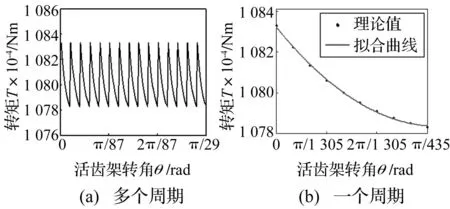
图3　输出转矩T随活齿架转角θ变化Fig.3 Output torque T changes with corner of teeth carrier θ

设活齿架间相对旋转角度为δθ，输出转矩增量为δTr，则转矩Tr在θ=θ0处展开成θ的泰勒级数为

Tr=Tr0+δTr=T(θ0)+T′(θ0)δθ+

(5)

活齿架输出转矩增量为

(6)

活齿与活齿架间啮合力Frj及啮合力Frj与输出转矩T的关系为

(7)

式中：Sj为固定齿理论齿形向径。

活齿与活齿架间非线性啮合刚度为

(8)

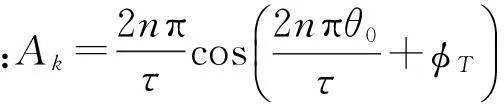
(9)

将式(8)、(9)代入式(2)，得矩阵形式的传动系统非线性动力学方程为

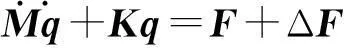
(10)

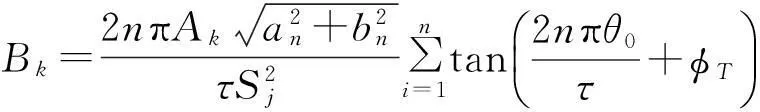
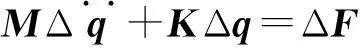
(11)

将式(11)正则化，得非线性自由振动正则方程为

(12)

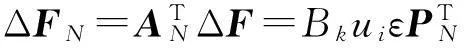
利用Linz Ted-Poincaré法求解式(12)，设

ΔqN=qN0+εqN1+ε2qN2+…

(13)

(14)

u=u0+εu1+ε2u2+…

(15)

将式(13)、(14)代入式(12)，令ε同次幂项相等，得近似微分方程为

(16)

初始条件为

(17)

解零次方程，得满足初始条件的解为

(18)

系统正则振型矩阵为AN，由Δq= ANΔqN可得原始坐标的ui为

(19)

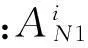
将式(19)代入式(16)可得一次近似方程组为

(20)

将式(18)代入式(20)，为消除久期项，令cos(ωit)的系数为0，则有

(21)

将式(21)代入式(20)，得一次近似方程的解为

(22)

将式(19)代入式(16)，得二次近似方程组为

(23)

将式(18)、(21)、 (22)代入式(23)，消除久期项得

(24)

将式(24)代入式(23)，得二次非线性近似解为

(25)

将式(18)、(22)、(25)代入式(13)可得正则坐标系下活齿系统时域位移响应，代入q=ANqN可得常坐标下位移响应。将式(21)、(24)、(25)代入式(14)可得系统非线性自由振动频率与派生系统固有频率关系。

4结果分析

4.1频率特性分析

取活齿数30，中心轮波齿数29，得系统传动比为30。将表1的传动系统参数代入非线性与线性频率关系式得传动系统非线性频率见表2，编号按软件计算结果顺序而非从小到大排列。表2中ω0i及ωi分别为线性与非线性固有频率；Δωi为非线性与线性频率差的绝对值；(Δωi/ω0i×100)为频率变化率。由于传动中活齿由15齿、16齿交替啮合，故表2为啮合齿数不同时的频率值。改变小参数ε、波发生器偏移量a、活齿半径rp及波发生器半径rs，得前两阶非线性与线性固有频率变化量随参数变化曲线，见图4。由表2、图4可知，①非线性存在使软件计算顺序所得到一、二阶非线性固有频率大于线性系统固有频率，三阶非线性固有频率小于线性系统固有频率；随阶次增加非线性与线性频率间差值增大，非线性现象增强。16齿啮合时非线性频率与线性频率间差值大于15齿的频率差值，即啮合齿数越少系统存在的非线性越强。②随ε增加一、二阶非线性与线性频率变化量增大，系统非线性现象增强。③随波发生器偏移量a增大非线性与线性频率变化量增大，系统非线性增强。因a增加使活齿与各构件间啮合力变大， 啮合刚度增大， 使系统非线性增强。④各阶非线性与线性频率变化量随rp及rs变化规律相同。增加rp或rs，非线性与线性频率变化量减小。可见一、二阶非线性强弱与rp或rs变化成正比，此因活齿与各构件间啮合刚度随rp或rs增加而减小。

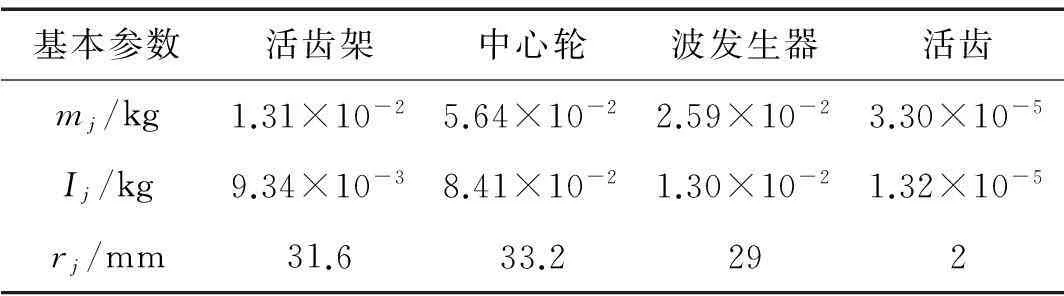
表1　传动系统参数

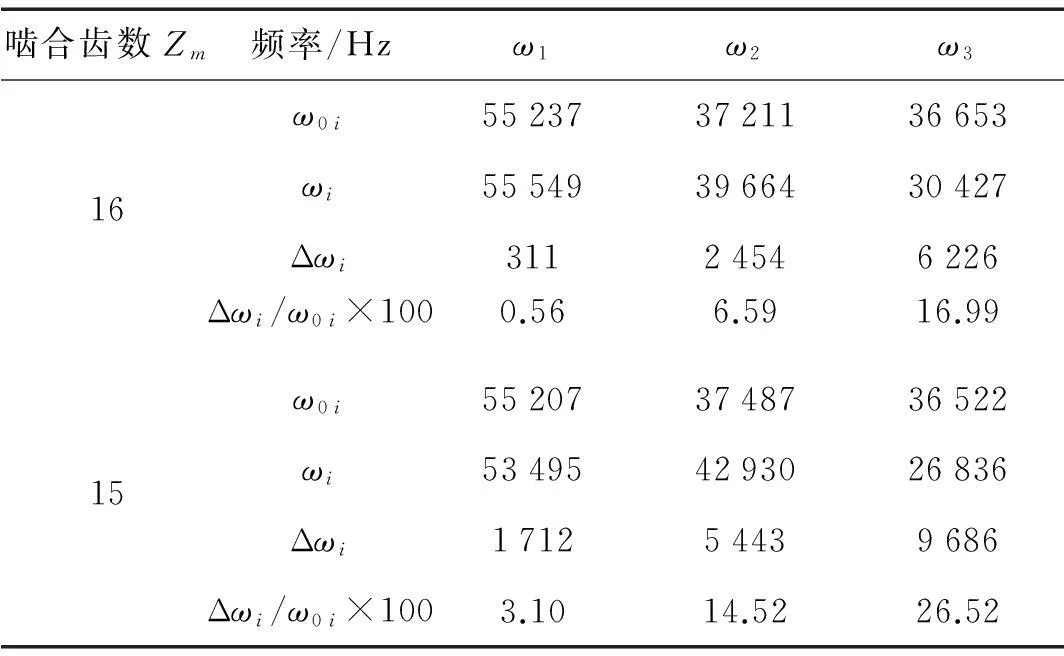
表2　传动系统非线性频率

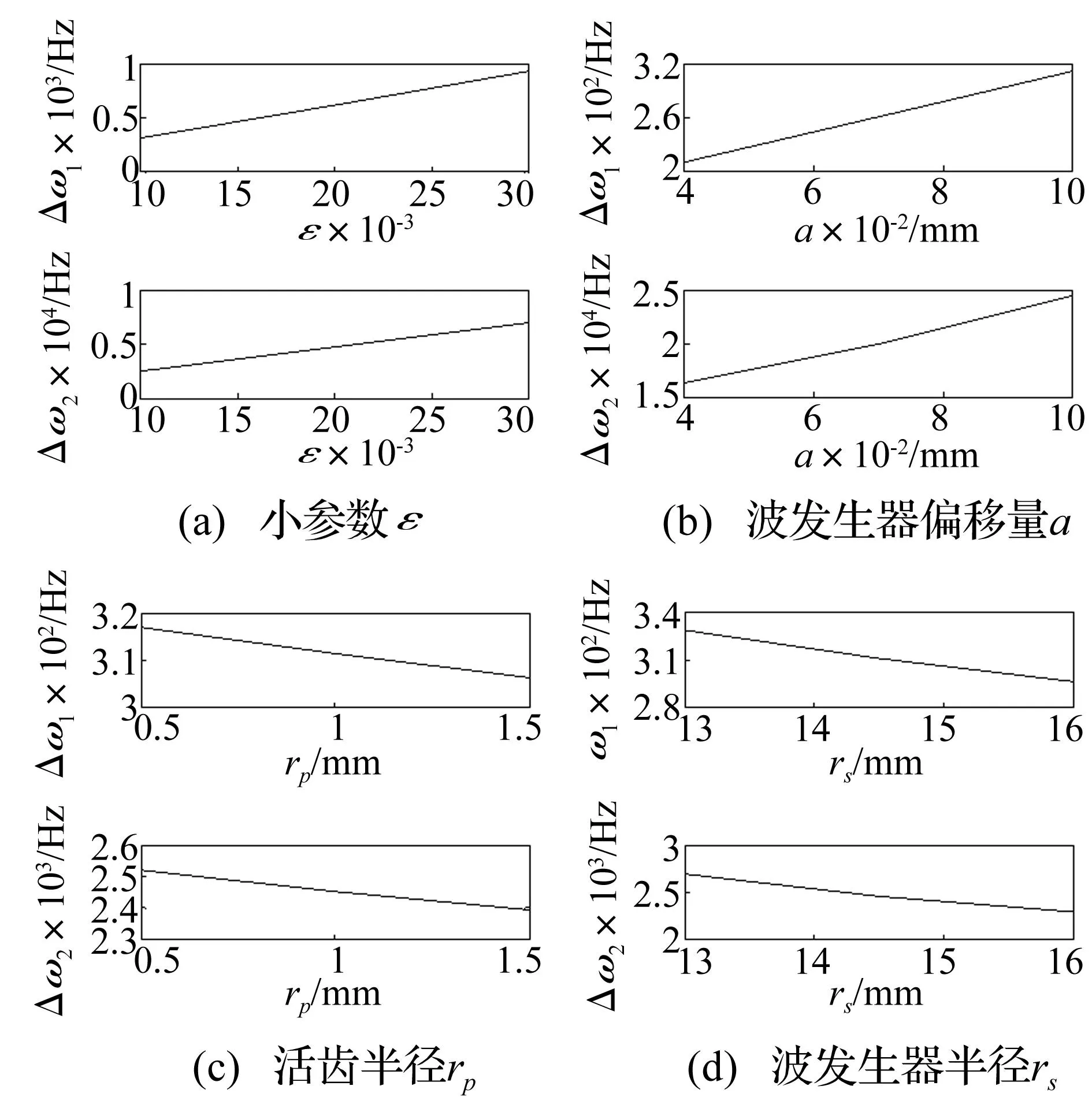
图4　非线性频率变化量随参数变化Fig.4 Nonlinear frequency variation changes with parameters

4.2位移响应分析

将传动系统参数代入q=ANqN所得非线性自由振动位移响应变化量，见图5。图5中选一个啮合活齿进行分析，而动力学建模时仅考虑活齿平面运动忽略转动，只求得Δxp1及Δyp1的响应；位移响应变化量指总响应减去零次响应所得。由图5看出，①波发生器非线性自由振动位移响应变化量表现为Δxs及Δys值较大，转动位移变化量Δus较小；中心轮三方向位移变化量Δxc、Δyc、Δuc均较小；活齿架Δur大于Δxr及Δyr；所选1号啮合活齿Δxp1及Δyp1均较大，且Δyp1>Δxp1。②各位移变化量中波发生器及活齿架位移变化量随时间变化较稳定，振幅变化周期性较强；中心轮、活齿位移变化量随时间变化周期性较紊乱，振幅变化规律性不强，易使传动系统出现随机振动，致传动系统运行不稳定。③系统位移变化量最大幅值出现在Δxs中，最小幅值出现在Δus中。原因为波发生器为活齿传动系统动力输入构件，且动力来自波发生器在两相互垂直方向摆动形成的谐波，非波发生器转动形成的谐波，故x,y方向力较大，u方向转矩较小。

图5　非线性自由振动位移响应变化量Fig.5 The displacement variation of nonlinear free vibration

5频率仿真验证

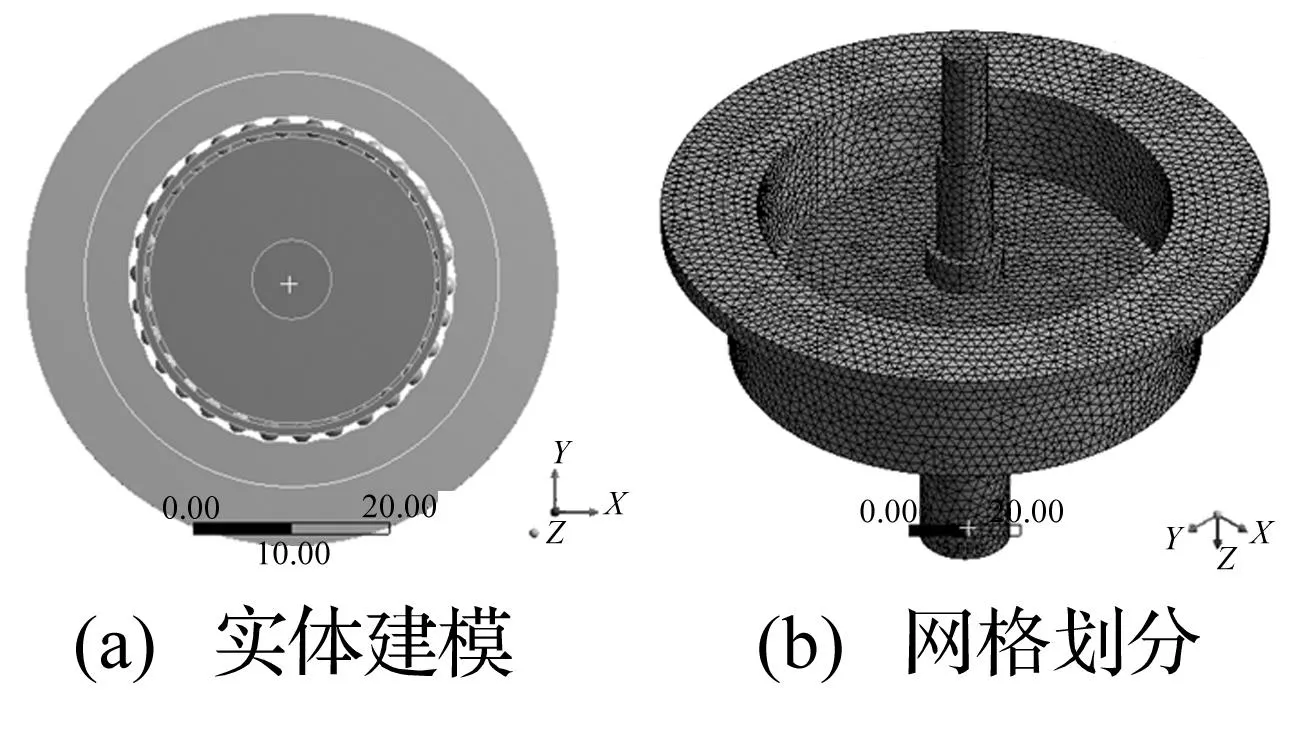
图6　传动系统有限元模型(mm)Fig.6 FEM model of drive system(mm)

用ANSYS有限元软件对活齿传动系统固有频率进行仿真计算。系统有限元模型见图6。建模时使活齿参与啮合个数调整为16齿，网格尺寸1 mm，对中心轮施加固定约束。参与啮合齿数不同时各构件所受啮合力会变化，活齿系统始终在15、16齿间等时交替变化，固有频率也会等时交替变化。本文选16齿啮合瞬时求解与分析。将部分模态计算结果与表2中16齿时非线性频率值对比，所得理论频率与仿真频率对比值见表3，有限元振型见图7。由表3、图7看出，表2中16齿啮合的理论计算频率在有限元仿真结果中均能找到对应值，且3阶频率中理论值与仿真值间最大误差为3.92%，从而验证本文动力学模型及动力学方程求解的正确性。由图7知，固有频率为57 724 Hz时对应的主振型为中心轮径向瘪曲振动；频率为40 463 Hz时主振型为波发生器与活齿架弯曲振动；频率为30 274 Hz时主振型为波发生器扭转振动。

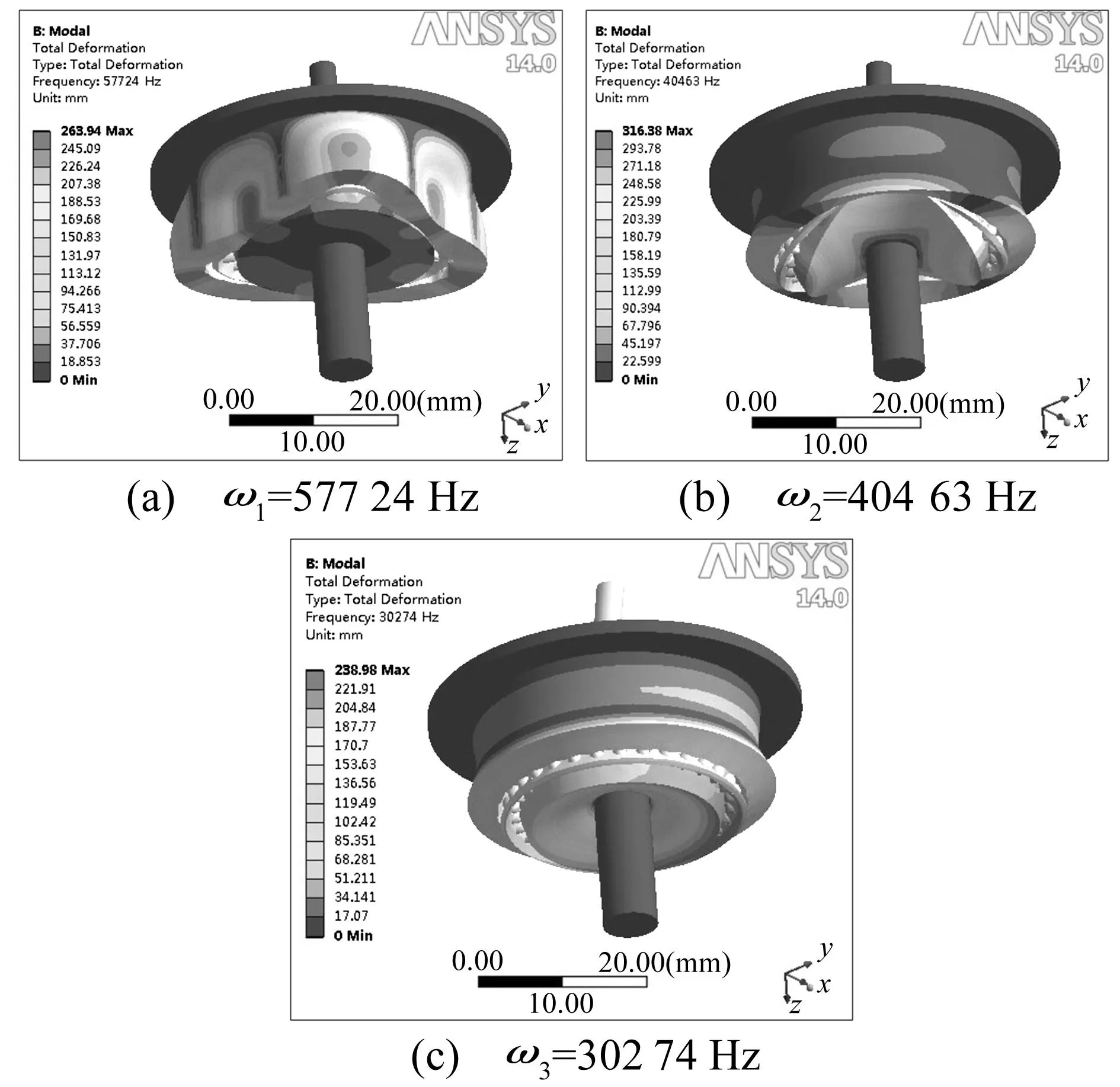
图7　有限元仿真振型图(mm)Fig.7 FEM vibration mode(mm)

ω1ω2ω3理论值/Hz555493966430427仿真值/Hz577244046330274误差/%3.922.010.50

6结论

通过所建机电集成压电谐波电机传动系统动力学模型及系统非线性动力学方程，采用Linz Ted-Poincaré法对非线性自由振动固有频率、位移响应进行求解，结论如下：

(1) 传动系统非线性根源由啮合齿数变化引起，啮合齿数越少系统非线性越显著；小参数ε及波发生器偏移量a对系统非线性频率影响较大；系统位移响应受非线性影响最明显、最微弱的分别为波发生器Δxs及Δus向。

(2) 由ANSYS有限元仿真验证本文固有频率求解的正确性。研究结果可为机电集成压电谐波电机参数设计及提高性能奠定理论基础。

参 考 文 献

[1] Liu Xiu-juan, Zhou Ke-chao, Zhang Xiao-yong, et al. Development, modeling and application of piezoelectric fiber composites[J]. Transactions of Nonferrous Metals Society of China (English Edition), 2013, 23(1): 98-107.

[2] Shigeki T. Spherical ultrasonic motor for pipe inspection robot[J]. Applied Mechanics and Materials, 2012, 186: 3-11.

[3] Jeong S, Cheon S, Park J, et al. Design and fabrication of three touch point thin ultrasonic rotary motor[J]. Ferroelectrics, 2014, 459(1): 143-152.

[4] 赵淳生. 南航助“嫦娥”完美登月[N]. 中国教育报, 2013-12-18(8).

[5] 邢继春,许立忠,梁永丽. 旋转式惯性压电电机的振子模型研究[J]. 振动与冲击，2010, 29(11): 105-109.

XING Ji-chun, XU Li-zhong, LIANG Yong-li. A vibrator model for a piezoelectric motor with rotary inertia[J]. Journal of Vibration and Shock, 2010, 29(11): 105-109.

[6] 季叶,赵淳生. 一种具有高转速的新型非接触式超声电机[J]. 压电与声光, 2006, 28(5): 527-529.

JI Ye, ZHAO Chun-sheng. A new type non-contact ultrasonic motor with higher revolution speed[J]. Piezoelectrics & Acoustooptics, 2006, 28(5): 527-529.

[7] Oliver B. Harmonic piezodrive-miniaturized servo motor[J]. Mechatronics, 2000, 10(4): 545-554.

[8] 辛洪兵,郑伟智. 压电谐波电机的研究[J]. 压电与声光, 2004, 26(2): 122-125.

XIN Hong-bing, ZHENG Wei-zhi. Study on harmonic piezomotor[J].Piezoelectrics & Acoustooptics,2004,26(2):122-125.

[9] 王长明,阳培,张立勇. 谐波齿轮传动概述[J]. 机械传动, 2006, 30(4): 86-88.

WANG Chang-ming, YANG Pei, ZHANG Li-yong.Summary of status on the harmonic gear driving technology[J]. Journal of Mechanical Transmission, 2006, 30(4): 86-88.

[10] Li Chong, Xing Ji-chun, Xu Li-zhong. Coupled vibration of driving sections for an electromechanical integrated harmonic piezodrive system[J]. AIP Advances,2014,4(3):031320.

[11] 梁尚明,张均富,徐礼钜,等. 摆动活齿传动系统振动的动力学模型[J]. 振动工程学报, 2003, 16(3): 285-289.

LIANG Shang-ming, ZHANG Jun-fu, XU Li-ju, et al. Dynamic model of swing movable teeth transmission system vibration[J]. Journal of Vibration Engineering,2003,16(3): 285-289.

[12] 张鹏,安子军. 摆线钢球行星传动动力学建模与固有特性分析[J]. 中国机械工程, 2014, 25(2): 157-162.

ZHANG Peng, AN Zi-jun. Dynamics model and natural characteristics of cyloid ball planetary transmission[J]. China Mechanical Engineering, 2014, 25(2): 157-162.

[13] 安子军,张鹏,杨作梅. 摆线钢球行星传动系统参数振动特性研究[J]. 工程力学, 2012, 29(3): 244-251.

AN Zi-jun, ZHANG Peng, YANG Zuo-mei. Research on properties for parametric vibration of cycloid ball planetary transmission system[J].Engineering Mechanics,2012,29(3):244-251.

Nonlinear free vibration of driving system of an electromechanical integrated harmonic piezoelectric motor

LIChong,XULi-zhong,GAOLi-chao

(School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)

Abstract:An electromechanical integrated harmonic piezoelectric motor which integrates piezoelectric driving, harmonic driving and movable tooth driving was designed and the working principle of the motor was discussed. Referencing the theory of planetary gear transmission, a dynamic model for the driving system was set up. Utilizing Linz Ted-Poincaré method, the equations of frequency characteristic and displacement response were deduced. The frequency variation and the characteristic of time response were analyzed. The ANSYS finite element software was applied to verify the frequencies provided. The results show, the nonlinearity of the driving system is caused by the changing of meshing teeth number during running conditions, and the fewer the meshing teeth number, the more obvious the nonlinear phenomenon of the driving system. The displacement response in the x direction of harmonic generator is the most affected by nonlinear phenomenon and that in the u direction is the least affected. A finite element simulation verifies the correctness of the dynamic model.

Key words:harmonic piezoelectric motor; driving system; nonlinear; free vibration; Linz Ted-Poincaré method

中图分类号:TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.002

通信作者许立忠 男，博士，教授，博士生导师，1962年1月生

收稿日期：2015-01-23修改稿收到日期：2015-05-22

基金项目：国家自然科学基金项目(51275441);河北省研究生创新资助项目(00302-6370001)

第一作者 李冲 男，博士生，1988年6月生