扁拱的面内非线性稳定与突变分析

朱晓蕾， 孙敦本

(南京林业大学 土木工程学院，南京　210037)



扁拱的面内非线性稳定与突变分析

朱晓蕾， 孙敦本

(南京林业大学 土木工程学院，南京210037)

摘要：通过位移、应变能突变分析扁拱结构受简谐荷载作用特性。采用谐波平衡法由扁拱非线性振动方程获得位移、频率关系尖点突变模型，据位移突变判别式分析扁拱非线性响应；用系统能量原理及有限元软件，借助突变理论导出结构失稳的应变能突变准则，并比较位移与应变能突变判别方式差异。结果表明，扁拱受简谐荷载作用的位移或应变能会发生突变，跨度、矢高及荷载对突变均有影响；用位移、应变能突变判别式计算结果基本一致，且各有优势及不足。

关键词：扁拱；突变理论；稳定；位移突变；应变能突变

扁拱作为特殊形式拱结构多用于厂房、体育馆、车站等。扁拱的动力响应与普通拱存在差异，因此研究扁拱结构的非线性稳定特性具有重要意义。早期计算拱结构所得为线性稳定解[1]，而对非线性动力行为研究[2-7]逐渐增多，但关于扁拱突跳失稳尤其用突变理论及能量判断扁拱结构突变研究较少[8-9]。

分析扁拱动力响应时仅考虑非线性因素无法阐明失稳的物理意义，微分方程建立的物理规律中不允许有突变及发散，因此可结合突变理论解决非线性问题。突变是系统对外部条件光滑变化的突然响应，突变理论为研究跃迁、不连续及突然质变的普遍适用方法[10]。由动荷载引起的扁拱非线性振动较复杂，类似“渐硬”弹簧振动。本文将位移、总应变能作为参考量判断结构是否发生突变，并通过有限元模拟验证其可行性。

1位移突变

1.1扁拱非线性振动方程及突变模型

扁拱指矢高较小的拱，其轴线长度较跨度不长多少，据文献[11]，若矢跨比满足式(1)可视为扁拱，即

(1)

式中：h为矢高；l为跨度；A为横截面积；E为弹性模量；H0为拱名义轴向力(四分点处轴力)，按经典理论计算即略去挠度对轴力影响，但需考虑拱的轴向压缩。

图1　扁拱结构示意图Fig.1 Structure diagram of shallow arch

设图1铰支扁拱满足假设，即平面弯曲，平截面假定，材料为线弹性，扁拱全长轴压力为常量且等于水平推力(矢跨比满足式(1)时，假设成立)。微段隔离体见图2。

图2　拱轴微段隔离体Fig.2 Micro section isolation body of arch axis

设扁拱作用荷载为

(2)

式中：F为荷载幅值；ω为荷载频率；t为时间。

扁拱偏微分运动方程为

(3)

式中：I为惯性矩；c为阻尼；ρ为密度；y0=y0(x)为初始拱轴线坐标；y=y(x,t)为变形后拱轴线坐标；w=w(x,t)=y(x,t)-y0(x)为位移方程。

设初始拱轴线y0(x)=hsin(πx/l)，双铰拱边界条件为

(4)

式中：“′”为对位移x求导。

基于Galerkin原理，满足式(4)的拱在任意时刻位移模式为

(5)

将式(5)代入式(3)并整理得(“·”表示对时间t求导)

βT3(t)=fcos(ωt)

(6)

式中：

(7)

(8)

(9)

(10)

(11)

扁拱的非线性振动可视为“渐硬”弹簧特性系统振动，方程中三次非线性项在响应中起主要作用[12]，可忽略二次非线性项影响，因此式(6)变为

(12)

式中：ω0为结构广义自振频率。

式(12)即为正弦型扁拱的非线性振动方程，也称为Duffing方程。

作用荷载、拱轴线及位移模式均设为正弦形式sin(πx/l)，目的为推导非线性振动方程过程中消去常数项便于理论计算及尽量减小公式误差。由于讨论的扁拱矢跨比较小，不同类型拱轴线形状无明显差别，荷载、拱轴线及位移模式形式对结果影响较小，故该假设合理。

由于外荷载fcos(ωt)按简谐运动规律变化，故式(12)的解可假设为

T(t)=Dcos(ωt+φ)

(13)

并略去三次谐波项可得

2ηωDsin(ωt+φ)=fcos(ωt)

(14)

(Acosφ-Bsinφ)cos(ωt)-

(Asinφ+Bcosφ)sin(ωt)=fcos(ωt)

(15)

使式(14)成立，则需满足

(16)

将式(16)等式两边分别平方相加得

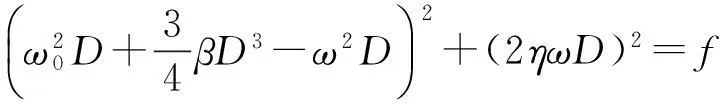
(17)

(18)

将式(17)等效为尖点突变模型平衡曲面标准形式z3+az+b=0，z含B2项且与α/β有关，推算可知各变量表达式为

(19)

(20)

(21)

平衡曲面反应位移最大值D与荷载频率ω的关系，故扁拱突变位移判别式为ΔD=4a3+27b2，ΔD>0结构稳定，ΔD<0结构失稳，ΔD=0为突变临界状态。

1.2位移突变分析

设跨度30 m、矢高0.5 m的正弦形铰支扁拱，拱轴材料为Q235的H型钢(H800×300×14×26)，横截面积0.026 74 m2，惯性矩0.002 92 m4，弹性模量206×109N/m2，密度7 850 kg/m3。施加形如式(2)且幅值为3 kN/m的简谐荷载，据式(19)～式(21)，只要已知阻尼比及荷载频率，即可通过ΔD判断结构的稳定性。由式(8)可知广义自振频率ω0=27.17 s-1，计算该频率附近的控制变量及位移判别式大小，结果见表1。由表1看出，ω=29 s-1时ΔD<0，说明扁拱在该频率简谐荷载作用下会失稳；ω小于或大于该频率时ΔD<0，扁拱稳定；结构突变临界点处于(28 s-1,29 s-1)及(29 s-1,30 s-1)两区域。

表1　位移判别式判断结果

分析ω在区间[20 s-1,36 s-1]时扁拱的突变情况与非线性响应特性。据式(19)～式(21)所得ω-D曲线见图3，可见频率与位移关系呈非线性，频率逐渐增大时位移达到最大值时减小，直接从a点突跳至b点，a→b之间的曲线段实际上是不可达状态；反之，若频率逐渐减小，位移会发生由小到大突变，即c→d，a，c分别为扁拱两失稳临界点。

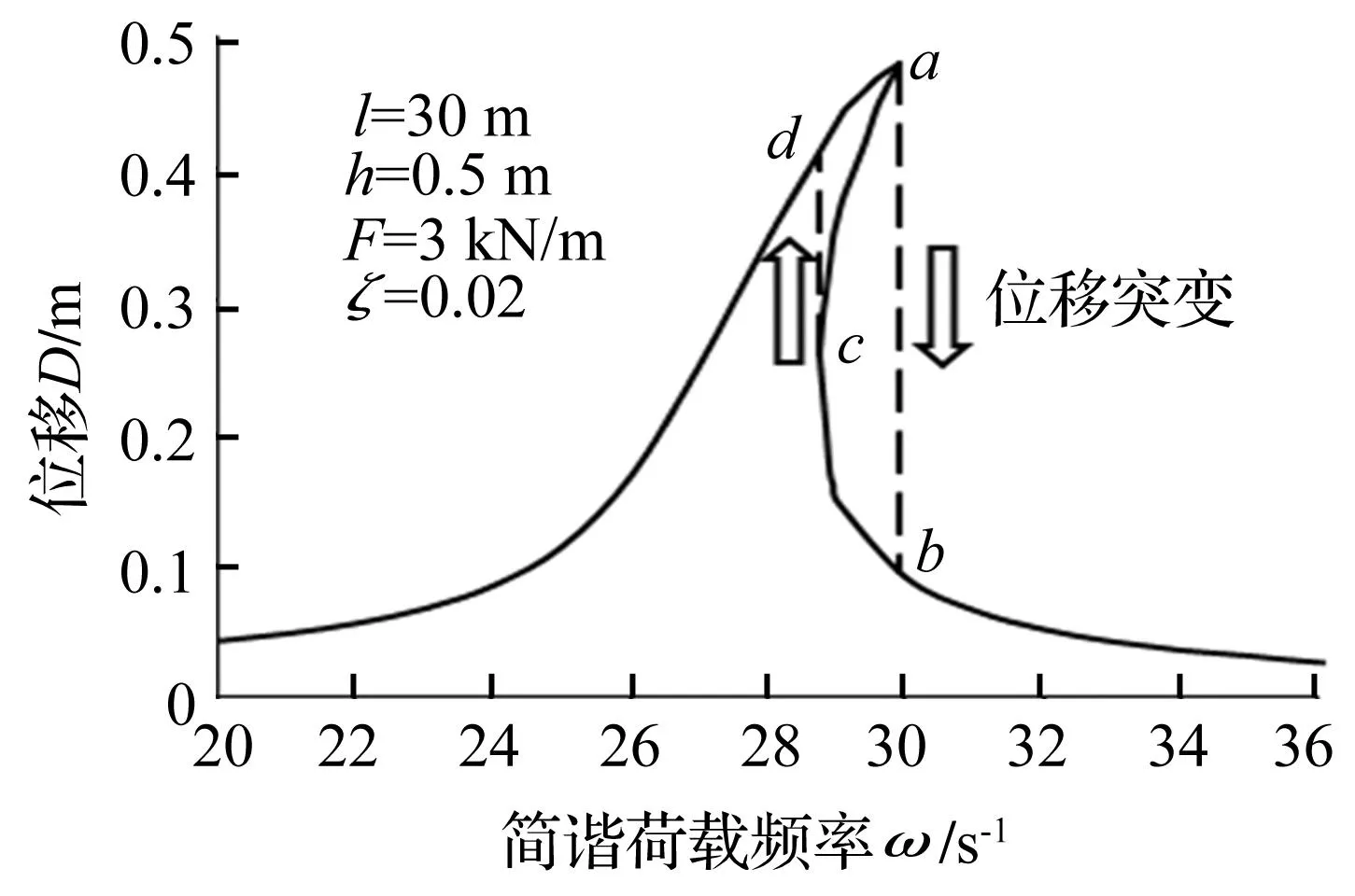
图3　ω-D曲线Fig.3 ω-D curve

由于钢结构的阻尼比为0.02，故在阻尼比不变条件下采用控制变量法改变扁拱跨度、矢高及荷载，该参数变化会引起ω0、β、f等改变从而导致判别式参数、大小改变，影响扁拱突变，见图4～图6。由3图看出，扁拱的非线性响应随跨度、荷载增大而增强，随矢高增大而减弱，矢跨比越小在简谐荷载作用下非线性特征越明显，越易发生突变致结构失稳。

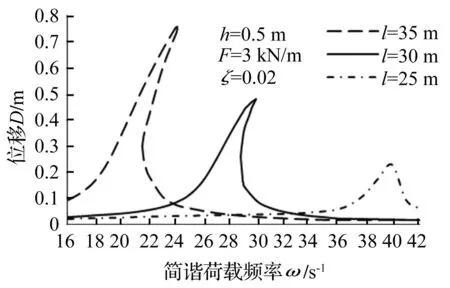
图4　跨度对突变影响Fig.4 The influence of span to catastrophe

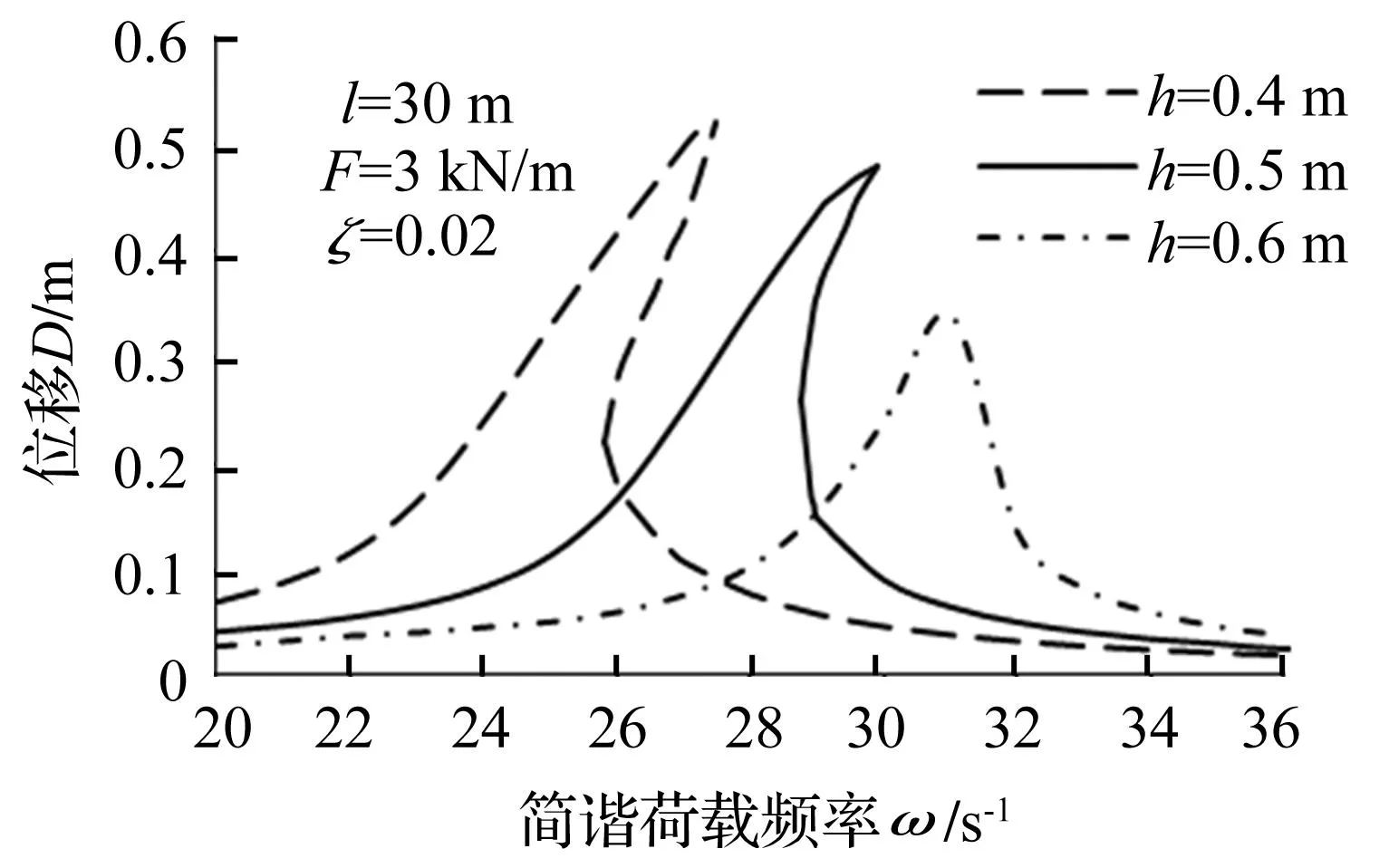
图5　矢高对突变影响Fig.5 The influence of rise to catastrophe

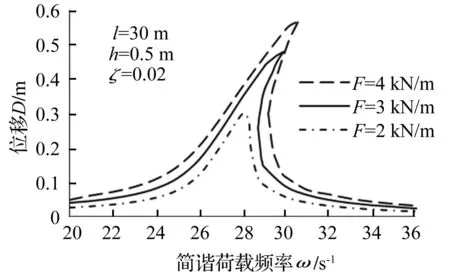
图6　荷载对突变影响Fig.6 The influence of load to catastrophe

2应变能突变

2.1应变能判别式建立

结构位移突变时其能量必会发生突变。若将扁拱视为系统，可据其应变能变化考察扁拱的稳定性。

若直接建立应变能Es与频率参数υ关系的4次拟合多项式Es=a3υ4/4+a2υ3/3+a1υ2/2+a0υ(a3、a2、a1、a0为多项式系数)，再正则化为尖点突变模型势函数形式Es=x4/4+ax2/2+bx+c(x为υ的函数，为状态变量，a、b、c为随υ变化的控制变量)，则x即频率参数的突变才会导致应变能突变。而计算过程中频率参数连续变化，表示系统势函数大小的应变能不可能发生突变。突变模型的物理含义为控制变量连续变化时引起状态变量突变，以应变能作为系统势函数与实际物理含义相悖[13]，故应将频率参数作为控制变量，应变能作为状态变量，如位移突变判断中，以连续变化频率ω的函数a、b作为控制变量，以会发生突变的位移D的函数z作为状态变量。

因此，考虑采用3次多项式拟合系统的平衡曲面，进行移项积分获得系统的势函数，进而对其正则化，再据突变特征值判定系统的稳定性。通过Abaqus进行数值模拟获得系统在不同频率下的应变能Es，通过最小二乘法准则进行拟合，使其化为3次多项式形式，以应变能为自变量、频率参数为因变量(设频率参数为υ，且υ=ω-20)。设该拟合多项式为

υ=a3Es3+a2Es2+a1Es+a0

(22)

式中：ai为多项式拟合系数。

移项并积分得

(23)

式中：C为常数项。

取系统势函数为

(24)

4次多项式(24)正则化为尖点突变模型的标准形式过程[14]。令Es=p-q，其中q=a2/3a3，代入式(24)得

V(Es)=b4p4+b2p2+b1p+b0

(25)

b1=-a3q3+a2q2-a1q+(a0-υ)

考虑b4>0情况，令

(26)

将式(26)代入式(25)，化为尖点突变模型势函数的正则形式为

(27)

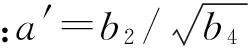
将式(27)对z′求导并令导数等于零，得平衡曲面方程z′3+a′z′+b′=0，且应变能突变判别式为ΔE=4a′3+27b′2，判别方式同位移判别式。

2.2应变能突变分析

以上节算例为例分析、比较两种判别方式差别。由有限元软件Abaqus计算可知该扁拱的一阶自振频率ω1=26.98 s-1，与式(8)所得广义自振频率相差不大。使简谐荷载频率ω从21 s-1开始递增，即频率参数υ从1开始递增，通过数值模拟可得不同υ对应的应变能。若是线性振动则υ=υ1≈7(ω=ω1≈27 s-1)系统发生共振时应变能最大，但非线性振动共振会发生偏移，由于扁拱呈“渐硬”弹簧特性，失稳处在υ>υ1位置的应变能会突然增大。υ-Es曲线关系见图7。由图7看出，从第7组数据开始进行3次多项式拟合。

图7　应变能的变化趋势Fig.7 The change trend of strain energy

前8及13组数据拟合曲线见图8。可见对拟合曲线进行积分获得以4次多项式表达的势函数，再正则化为式(27)形式，由判别式判断结构是否失稳。结果见表2。由表2看出，突变位置在频率为29 s-1附近区域，即频率逐渐增大或减小、判别式ΔE由正到负穿越分叉集时能量突变。因尖点突变控制变量满足条件，从而导致整个系统产生突变，即状态变量(应变能)发生突跳，扁拱从失稳前某平衡位置跳跃到失稳后另一平衡位置。

图8　前8及13组数据3次拟合曲线Fig.8 Three fitting curves of the first 8 and 13 dates

ωa'b'ΔE状态2610.584.600>0稳定279.1583.478>0稳定289.454-5.747>0稳定29-6.154-5.051<0失稳30-6.317-16.65>0稳定

3两种判别方式比较及可行性

比较表1、表2结果知，扁拱失稳的简谐荷载频率均为29 s-1，即采用位移、应变能判别式判断结果几乎相同。应变能大小可由有限元分析获得，因此以应变能为判据无需获知扁拱结构的非线性振动方程，但拟合多项式及正则化过程较繁琐，若只需确定结构在某频率下是否突变，用应变能突变判断方式较简便；若了解结构非线性振动特性及突变范围，可据位移与频率的突变关系。

图9　理论计算与数值模拟的ω-D曲线Fig.9 ω-D curves of theoretical calculation and numerical simulation

由Abaqus计算[20 s-1,36 s-1]区间内各频率位移值，所得ω-D曲线见图9。由图9看出，有限元数值模拟虽无法获得位移突变结论，但频率在29 s-1附近时位移有显著增大或减小，与理论分析结果整体趋势一致。位移在荷载频率大于一阶固有频率(广义自振频率)时达最大值，说明位移突变的判断方式具有可行性；应变能及位移突变的判断结果相似，亦具有可行性。数值模拟可用于分析一般形式荷载、拱轴线及位移模式的扁拱。

4结论

(1)利用突变理论分析扁拱受简谐荷载作用的非线性稳定与突变，分别由位移、应变能与荷载频率尖点突变模型分析比较。在某些条件下荷载频率大于(广义)自振频率时扁拱会发生突变。

(2)扁拱的动力响应为非线性的，且程度随跨度、荷载增大及矢高减小而加强。非线性程度较明显、简谐荷载频率达到一定值时位移或应变能突变，会对结构稳定产生较大影响，可能因突跳发生破坏。

(3)可利用突变理论分析扁拱的非线性响应，解释面内失稳的突变现象。位移、应变能突变均可判断扁拱是否失稳，两种方法各有优势及不足，但均具有可行性，可为实际工程提供理论参考。

参 考 文 献

[1] Austin W J, Asce F. In-plane bending and buckling of acrhes[J]. Journal of the Structural Division, 1971, 97(5): 1575-1592.

[2] Tien W M, Namachchivaya N, Malhotra N. Non-linear dynamics of a shallow arch under periodic excitation.Ⅱ:1:1 internal responce[J]. International Journal of Non-linear Mechanics, 1994, 29(3): 367-386.

[3] Bi Q, Dai H H. Analysis of non-linear dynamics and bifurcations of a shallow arch subjected to periodic excitation with internal resonance[J]. Journal of Sound and Vibration, 2000, 233(4): 553-567.

[4] Mallon N J, Fey R H B, Nijmeijer H, et al. Dynamic buckling of a shallow arch under shock loading considering the effects of the arch shape[J]. International Journal of Non-linear Mechanics, 2006(41): 1065-1075.

[5] 易状鹏,张勇,王连华. 弹性约束浅拱的非线性动力响应与分岔分析[J]. 应用数学和力学,2013,34(11):1182-1196.

YI Zhuang-peng, ZHANG Yong, WANG Lian-hua. Nonlinear dynamic response and bifurcation analysis of the elastically constrained shallow arch[J]. Applied Mathematics and Mechanics, 2013,34(11):1182-1196.

[6] 郭俊材,于兰峰,朱小龙,等. 基于有限元法的抛物线拱稳定性及动力学分析[J]. 机械设计与制造,2013,6:72-74.

GUO Jun-cai, YU Lan-feng, ZHU Xiao-long, et al. Stability and dynamic analysis of parabolic arch structure based on finite element method[J]. Machinery Design and Manufacture, 2013, 6:72-74.

[7] 黄繁,戴绍斌,黄俊. 正弦型黏弹性拱的非线性动力学行为研究[J]. 振动与冲击,2015,34(7):174-177.

HUANG Fan, DAI Shao-bin, HUANG Jun. Nonlinear dynamic behaviors of sine type viscoelastic arch[J].Jornal of Vibration and Shock,2015,34(7): 174-177.

[8] 陈浩军,杨润生. 扁拱平面内失稳的突变模型分析[J]. 长沙交通学院学报,1991,7(4): 83-88.

CHEN Hao-jun, YANG Run-sheng. The analysis of catastrophe model of flat-arch unstability in load plane[J]. Journal of Changsha Communications Institute,1991,7(4): 83-88.

[9] Breslavsky I, Avramov K V, Mikhlin Y, et al. Nonlinear modes of snap-through motions of a shallow arch[J]. Journal of Sound and Vibration, 2008, 311(1/2): 297-313.

[10] Saunders P T,著.凌复华,译.突变理论入门[M]. 上海：上海科技学术文献出版社,1983.

[11] 项海帆,刘光栋. 拱结构的稳定与振动[M]. 北京：人民交通出版社,1991.

[12] 陈树辉. 强非线性振动系统的定量分析方法[M]. 北京：科学出版社,2007.

[13] 潘岳,李爱武. 关于“基于突变理论的高拱坝失稳判据研究”的讨论[J]. 岩土工程学报,2012,34(5):965-967.

PAN Yue, LI Ai-wu. Discussion on “instability criteria for high arch dams using catastrophe theory”[J].Chinese Journal of Geotechnical Engineering,2012,34(5):965-967.

[14] 郑东健,雷霆. 基于突变理论的高拱坝失稳判据研究[J]. 岩土工程学报,2011,33(1): 23-27.

ZHENG Dong-jian, LEI Ting. Instability criteria for high arch dams using catastrophe theory[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 23-27.

Nonlinear in-plane stability and catastrophe analysis of shallow arches

ZHUXiao-lei,SUNDun-ben

(School of Civil Engineering, Nanjing Forestry University, Nanjing 210037, China)

Abstract:The catastrophe properties of shallow arches under harmonic load were analyzed by adopting the catastrophe criteria of displacement and strain energy respectively. A cusp catastrophe model that expresses the relationship between displacement and frequency was obtained from the nonlinear vibration equation by the harmonic balance method and the nonlinear responses of shallow arches were analyzed according to the criterion of displacement catastrophe. The strain energy catastrophe guideline of instability was obtained according to catastrophe theory by using the system energy principle and finite element software. The differences between the results by the two catastrophe criteria were discussed. The results show that the displacement or strain energy of shallow arches both can have a sudden change. Span, rise and load have impact on catastrophe. The results are almost the same, calculated according to either of the two catastrophe criteria, each has advantages and disadvantages.

Key words:shallow arch; catastrophe theory; stability; displacement catastrophe; strain energy catastrophe

中图分类号:O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.008

通信作者孙敦本 男，高级工程师，1964年9月生

收稿日期：2014-10-28修改稿收到日期：2015-04-03

基金项目：江苏高校优势学科建设工程资助项目

第一作者 朱晓蕾 女，硕士生，1990年8月生