基于全局灵敏度分析的某自动装填机构轻量化设计

蒋清山， 钱林方， 陈光宋

(南京理工大学 机械工程学院，南京　210094)



基于全局灵敏度分析的某自动装填机构轻量化设计

蒋清山， 钱林方， 陈光宋

(南京理工大学 机械工程学院，南京210094)

摘要：针对某自动装填机构轻量化设计中出现参数多、模型计算量大等问题，提出将全局灵敏度分析与代理模型技术相结合的优化策略。通过基于Morris轨迹的全局灵敏度分析从32个系统参数中确定14个关键参数，基于拉丁超立方采样技术及径向基函数神经网络技术(Radial Basis Function Neural Networks, RBFNN)建立系统响应关于关键参数的代理模型，用多岛遗传算法对系统参数进行优化求解，致机构重量下降21.8%。数值检验结果表明仅含关键参数的代理模型预测精度较高，证明该方法在多参数复杂系统结构轻量化设计中的有效性。

关键词：自动装填；全局灵敏度分析；轻量化设计；参数优化

自动装填系统虽能大幅提高大口径自行火炮射速、有效降低乘员工作强度，但较大程度上会影响全炮的重量指标。装填系统机构复杂，涉及构件参数较多，设计时难免偏于保守。而对装填系统进行轻量化设计，可保证装填系统使用性能前提下提升全炮有效作战载荷比。葛建立等[1-4]对自行火炮的炮塔、负重轮轮毂及上架等常规组件进行结构轻量化改进取得显著效果，而关于自动装填系统轻量化设计研究较少见。

对复杂多参数系统优化过程中通常采用代理模型技术以提高求解效率，但参数过多时建立代理模型难度较大。实际设计、分析中发现，复杂系统往往只有部分参数对系统某些特性起主导作用，且参数间可能存在一定耦合关系，而其它参数对系统特性影响较小甚至可忽略[5]。后者不仅增加代理模型构建难度且数据中所含噪声会使代理模型出现过拟合而降低求解精度。结合灵敏度分析法在关键参数提取、模型缩减的准确性及代理模型技术求解的高效性会使复杂系统优化求解问题更高效、准确。

本文采用基于Morris轨迹的全局灵敏度分析方法对某自动装填机构进行关键参数提取及规模缩减，用径向基神经网络(RBF NN)技术构建关键参数代理模型，在保证架体支撑刚度不下降前提下通过优化各部位壁厚参数及不同材料组合进行轻量化设计。

1装填机构轻量化建模

1.1装填机构有限元建模

自动装填机构由两组平行六杆机构与弹射输弹机组成，见图1。弹射输弹机安装于六杆机构末端并可绕点O旋转，调整其与水平面夹角θ可满足不同射角装填要求。在输弹力F作用下，弹丸在短时间内获得较大速度并依其惯性进入身管，以约3 m/s速度完成卡膛[6]。弹丸加速过程中会对输弹机产生较大反作用力F′作用于架体O点。架体通过油缸两腔闭锁以其自身刚性对输弹机起一定支撑作用，保持输弹通道通畅及弹丸姿态稳定。

据实际结构尺寸进行简化处理后建立的有限元模型见图2。

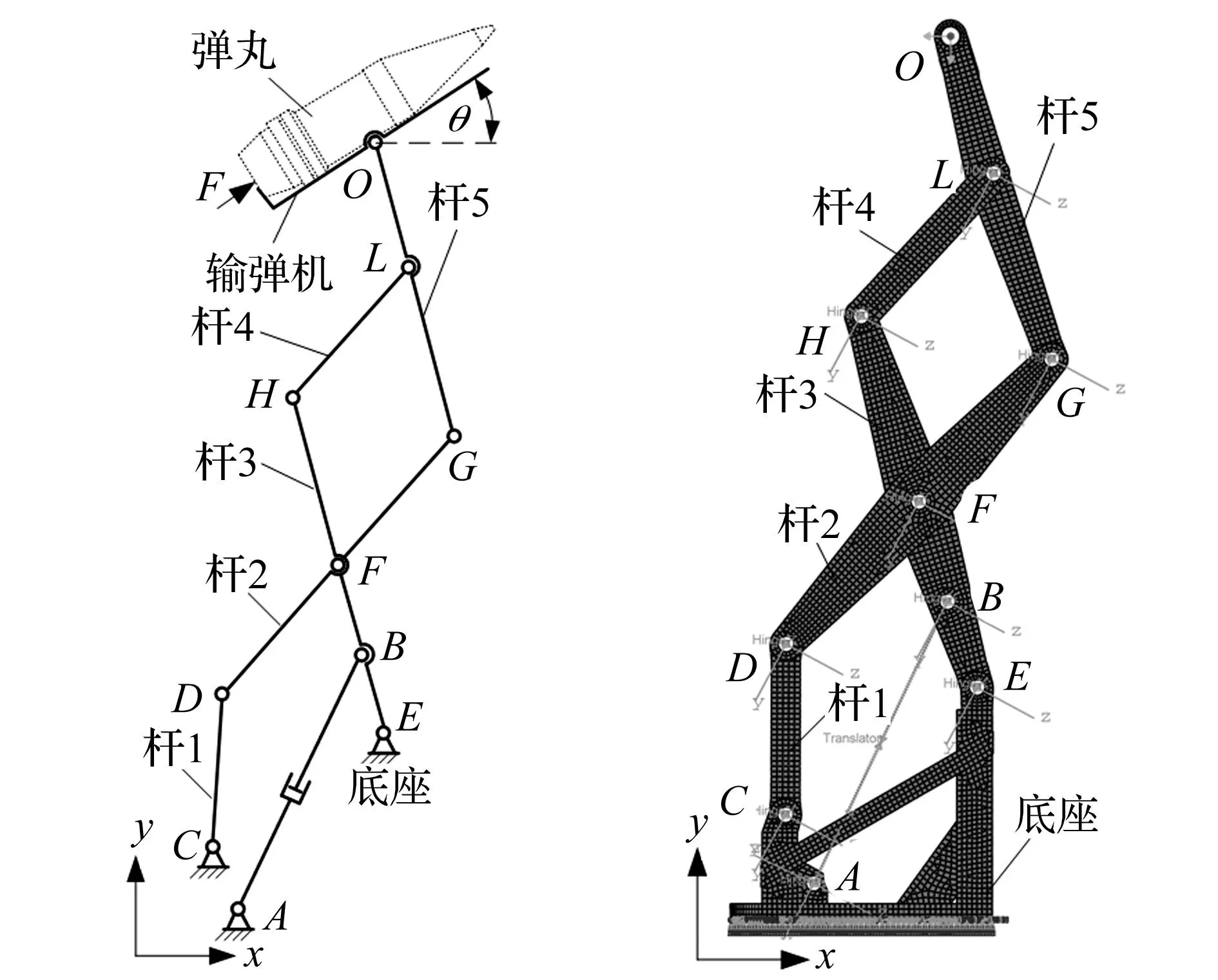
图1 装填机构简图Fig.1Sketchofloadingmechanism图2 有限元模型Fig.2FEMmodel

由试验知，输弹过程中架体略有变形，但各射角下弹丸运行均较平稳，整体满足装填性能要求。组件基座与杆3的结构组成见图3，可见装填机构组件大多由板件拼焊而成以减小机构质量。为满足系统重量指标要求，需在保证系统结构刚度不下降前提下进一步减小机构质量，通过更换轻质材料、优化板件厚度参数等并结合有限元刚强度分析对装填机构进行轻量化设计。

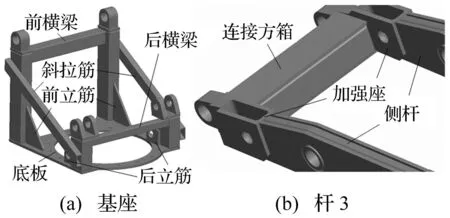
图3　基座与杆3组成Fig.3 Components of base and link 3

有限元建模中对板件进行抽中面处理，用壳单元划分以减小网格数量、提高计算效率及方便参数化设计。据有限元模型(图2)添加边界条件及载荷。①构件连接。因实际各构件间通过销轴连接，模型用abaqus机构仿真的Hinge连接；②约束。据实际装置的铰接关系及底座固定安装，基座底面采用全约束；③载荷。在O点添加作用力F′。据动力学仿真[7]知，不同角度的最大输弹载荷基本相同，考虑推头与弹丸初始时刻未完全贴合，会存在一定冲击，故F′的取值为

F′=Fcnv/ir

(1)

式中：Fc为输弹油缸载荷；ir为输弹油缸活塞杆到推头传速比；nv为考虑冲击的动载系数。

由于架体理论上不受侧向载荷，故以O点最大位移U及角位移Ur作为支撑刚度评价标准。

1.2轻量化设计

装填机构轻量化设计可描述为

(1) 设计变量

以各组件中板件厚度及材料参数x=(x1,x2,…,xi1,xi1+1,…xi1+i2,…,xi1+i2…+i6,xM1,xM2,…,xM6)为设计变量，其中前i1项表示第一类组件结构参数，i2项表示第二个组件结构参数，以此类推，xM1,…,xM6分别为六种组件的材料参数。

(2)目标函数

(2)

式中：mj为第j类组件质量之和。

(3)约束条件

(3)

式中：σj为杆j最大应力，σ6为基座最大应力，均可通过编程读取结果文件对各组件节点应力进行排序获得；[σ]j为组件j所用材料许用应力；U0，Ur0分别为原系统参数下点O最大位移及角位移，可直接从结果文件中读取；tmin，tmax分别为适合焊接工艺的最小、最大尺寸。

由于装填机构轻量化设计所含设计变量较多，直接对模型优化不具可行性。因此需通过灵敏度分析技术对模型规模进行缩减，并结合代理模型技术提高其求解效率。

2基于灵敏度分析的装填机构轻量化设计

2.1径向基函数神经网络技术

图4　径向基神经网络拓扑结构Fig.4 Topology of RBF NN

系统输入通过高斯函数实现向隐层空间非线性映射，使网络输出直接通过隐层中心响应的线性叠加，表示为

(4)

式中：(i=1, 2…,h)为隐层中心编号；(j=1, 2…,m)为网络输出编号；(k=1, 2…,n)为样本输入节点编号；σ为扩展参数，用于控制基函数宽度，以高斯函数作为径向基函数时σ的启发式关系设置[8]为

(5)

式中：dmax为所选中心间最大欧式距离。

径向基神经网络为局部逼近网络，每次学习时只需对少量权值进行修正，泛化能力及学习收敛性良好。理论上已证明该网络能在有限范围内以任意精度逼近任意有界的连续函数。

2.2基于Morris轨迹的全局灵敏度分析

全局灵敏度分析在所有参数同时变化下分析其对系统输出影响程度及参数间相互作用[9]，分为定性、定量全局灵敏度分析两种。

2.2.1基本因素法

基本因素法基于OAT(One-at-a-Time)进行，即假定系统含k个输入参数x=(x1,x2, …,xk)T∈Rk，系统输出为y(x1,x2, …,xk)，若仅让第i个参数增加或减少一固定小量Δ，则输出变为y(x1, …xi,xi+1, …,xk)。参数xi关于Δ的基本因素定义为

(6)

由式(6)看出，基本因素法为局部灵敏度分析法，为进行全局灵敏度分析，需结合高效采样技术在全变量域进行EEi计算。

2.2.2Morris轨迹法

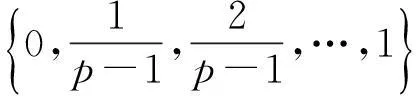
通过设计空间内随机生成m条Morris轨迹并计算各参数的基本因素，可得均值μi及均方差σi，即

(7)

(8)

为避免EEi非单调性造成的相互抵消，文献[10]将μi的定义修改为

(9)

通过灵敏度因子可对该参数重要程度进行判定：①若μ*i很小，则该输入参数不重要，可忽略；②若μ*i较大、σi较小，则该参数与系统输出具有较强的线性相关性，且与其它参数相互作用较弱；③若μ*i、σi均较大，则该参数与系统输出具有较强的非线性相关性，且/或与其它参数存在较强相互作用。

基于Morris轨迹法的全局灵敏度分析法不能对系统参数的重要程度进行定量分析，但通过有限数量样本计算可较快识别出灵敏度较大系统参数。据该全局灵敏度分析法求解流程知，参数越重要越易在灵敏度分析中获得响应，因此只要取得合理阈值则不会遗漏系统的重要参数。

为综合考虑μ*i及σi影响，在平面直角坐标系内记点(μ*i,βσi)的矢径为SRi作为第i维参数灵敏度评价系数，即

(10)

式中：β为σ相对μ*的权重系数。本文视σ与μ*为等权重取β=1。通过计算SRi可方便快捷为参数的重要程度提供较直观的判断参考，因此解决工程实际问题中具有较好的适用性。

2.3基于灵敏度分析及代理模型的轻量化设计

完成装填机构建模后通过变更各组件材料参数、各拼焊板件厚度分析计算，即可获得不同参数及材料分布的机构响应。由于系统参数较多，需通过基于Morris轨迹的全局灵敏度分析法对影响装填机构支撑刚度的结构、材料参数等进行提取。利用拉丁超立方采样技术在关键参数设计空间内随机生成足够样本点并计算O点位移响应，用所得数据作为径向基神经网络训练样本建立O点位移关于关键参数的代理模型并满足一定精度要求。通过优化算法对代理模型中关键参数优化计算获得满足支撑刚度要求的最小质量。基于灵敏度分析及代理模型技术的装填机构轻量化设计流程见图5。

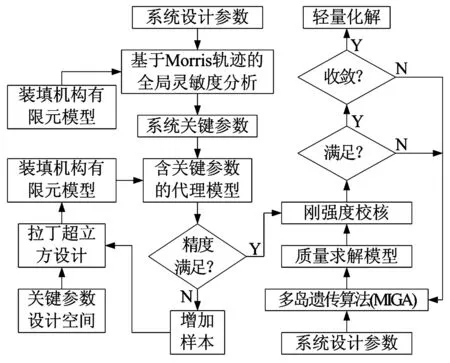
图5　装填系统轻量化设计流程图Fig.5 Flowchart of lightweight design for loading system

3算例分析

3.1轻量化设计实例

以本文装填机构为例，6类组件共含结构参数26个，材料参数6个。选钢与铝合金两种材料进行组合，参考输弹动力学仿真中推头与弹丸碰撞力规律，取动载系数nv=1.5，F′=4 800 N，tmin=3 mm，tmax=18 mm， [σ]=160 MPa。据初始参数计算得输弹载荷作用下装填机构位移、应力分布见图6，其中U0=2.51 mm，Ur0=0.259°，最大应力95.9 MPa。

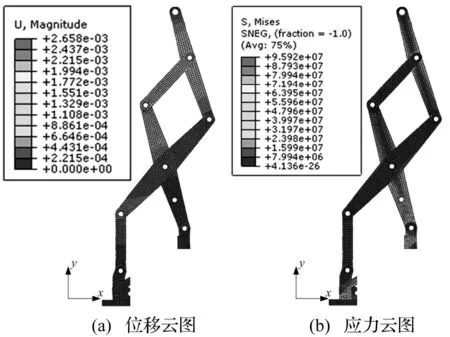
图6　装填机构位移及应力云图Fig.6 Contour banded plot of displacement and stress

据式(10)进行灵敏度分析并以灵敏度最高参数即G3_Material为参照对所有参数相对灵敏度进行排序，见表1。其中前缀Gi_*为组件杆i的参数；Base_*为组件基座参数；*_Material为组件所用材料。其中加粗字体表示相对灵敏度大于3%、并设为关键参数，计14个。在描述μ*i及σi的直角坐标系第一象限中，18个非关键参数灵敏度评价系数小于最大值的3%，即坐标点落在小于0.1%区域内，而其余14个坐标点则覆盖99.9%区域，因此可忽略18个非关键参数影响。由表1看出，装填机构关键参数主要分布在杆2、杆3、杆5及基座中。按图5流程生成400个采样点进行有限元计算，将所得数据作为径向基神经网络训练样本构建O点位移关于14个关键参数的代理模型。同理可提取影响各组件最大应力的关键参数，并构建代理模型进行约束条件校核。对等效为二力杆构件可直接由理论公式校核计算。

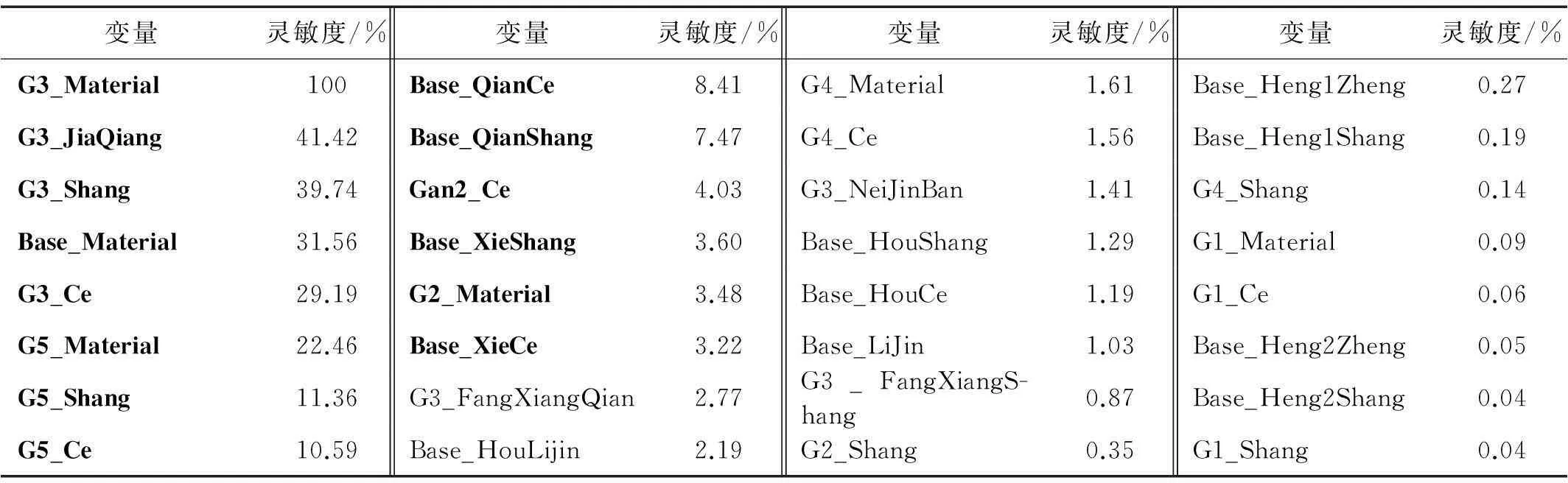
表1　设计变量相对灵敏度

基于代理模型优化前后各参数取值见表2。在最优解条件下代理模型的O点位移预测结果为：U=2.27 mm，Ur=0.251°，最大应力出现于杆3为94.5 MPa，能满足位移及许用应力条件。此时装填机构质量为88.01 kg，较原112.63 kg下降21.8%，减重效果十分显著。

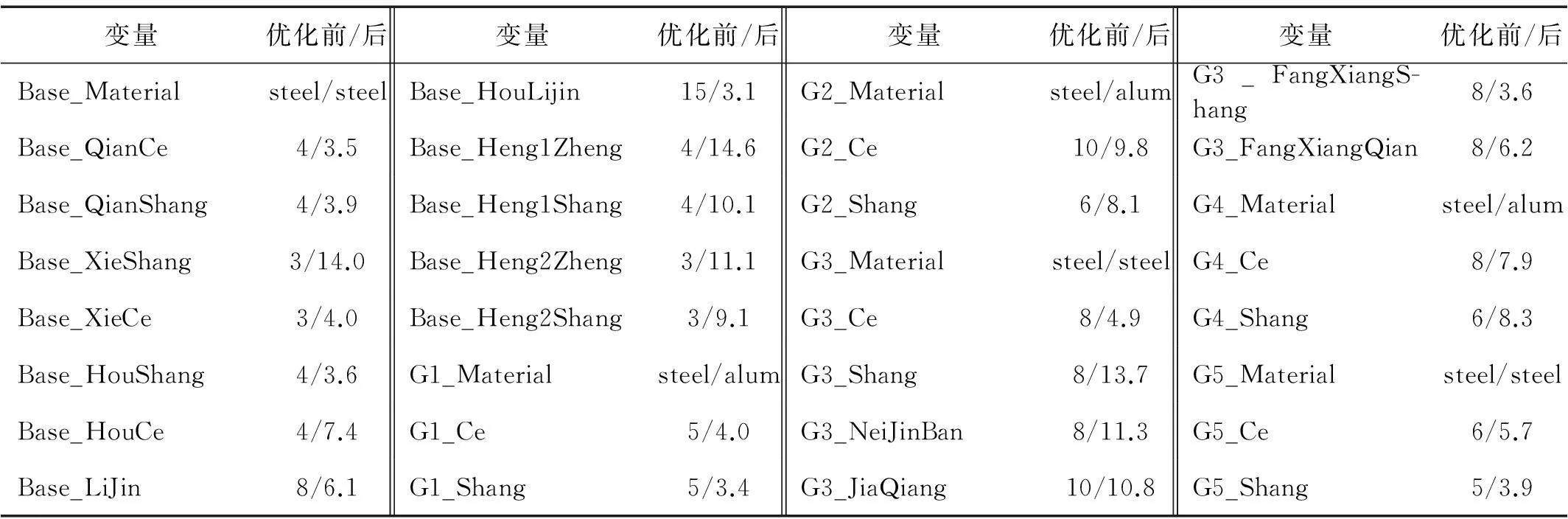
表2　优化前后参数对比

3.2数值验证与分析

为进一步验证代理模型的预测精度，将优化解代入有限元模型，所得装填机构位移、应力分布见图7，与代理模型预测结果对比见表3，杆3应力分布见图8。可见模型缩减建立的代理模型预测与有限元模型计算的位移误差不超过8%，杆3应力预测误差为12.5%，其它应力预测误差不超过3%。杆3最大应力处出现应力集中现象，使代理模型预测难度大大增加，致预测精度下降，但代理模型整体仍能满足工程实际应用的精度要求。

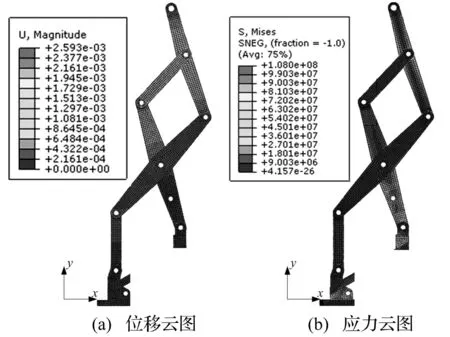
图7　优化后位移、应力云图Fig.7 Contour banded plot of displacement and stress after optimization

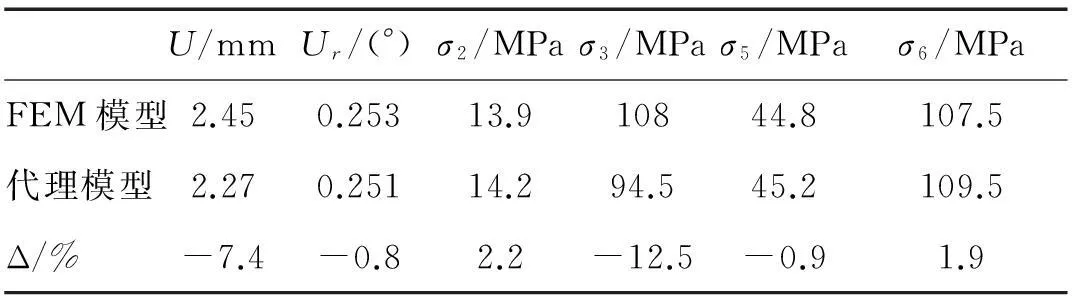
U/mmUr/(°)σ2/MPaσ3/MPaσ5/MPaσ6/MPaFEM模型2.450.25313.910844.8107.5代理模型2.270.25114.294.545.2109.5Δ/% -7.4-0.82.2-12.5-0.91.9

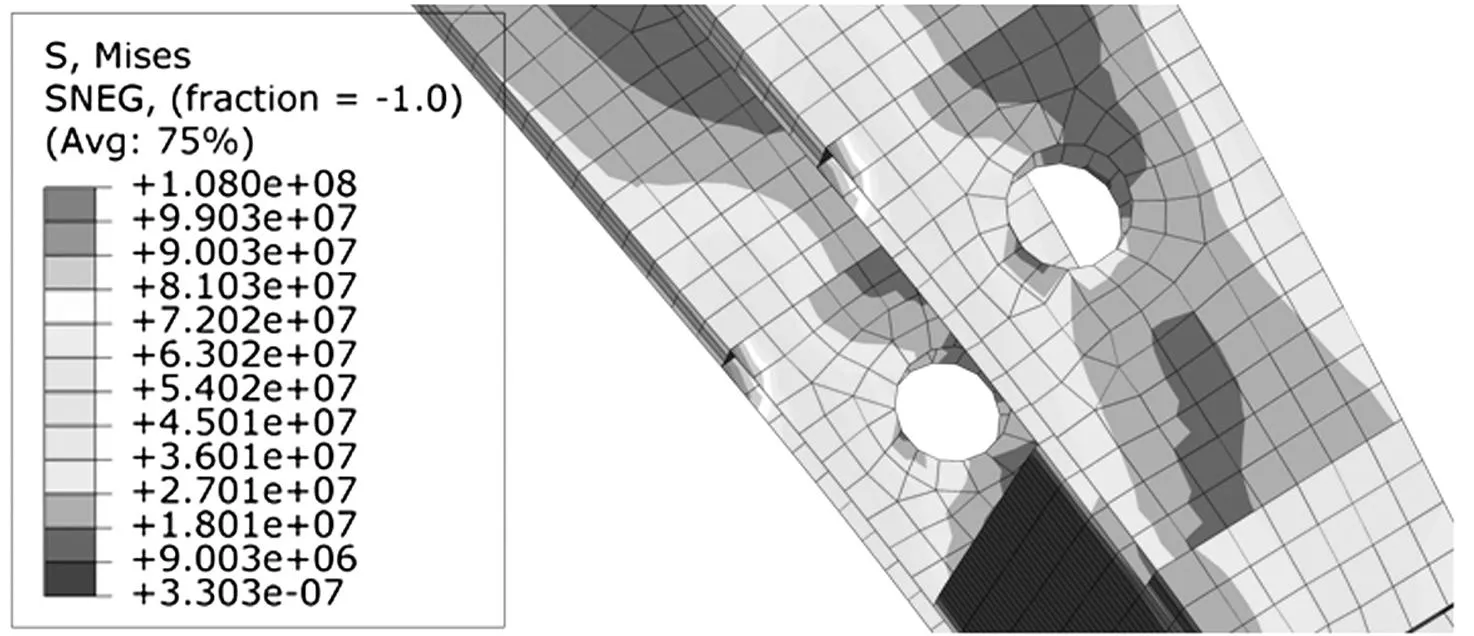
图8　杆3的应力分布Fig.8 Contour banded plot of link 3

4结论

基于Morris轨迹的全局灵敏度分析方法及代理模型技术的优化策略，结合算例仿真，结论如下：

(1)由灵敏度分析将参数从32个缩减到14个，代理模型在数值检验中的位移预测误差小于8%，应力误差不超12.5%，表明仅含关键参数的代理模型仍具有较高的预测精度。

(2)通过结构参数优化及材料组合实现机构重量下降21.8%，减重效果明显，且可进行多种材料组合优化，实现材料最优分布。

(3)优化策略对装填系统轻量化设计具有较好的指导意义，且可为其它复杂系统规模缩减及优化提供参考。

参 考 文 献

[1] 葛建立,过斌,杨国来,等. 基于参数优化的炮塔轻量化设计[J]. 火炮发射与控制学报, 2001(2): 82-85.

GE Jian-li, GUO Bin, YANG Guo-lai, et al. Lightweight design of the gun turret based on parameter optimization [J]. Journal of Gun Launch & Control, 2001(2): 82-85.

[2] 潘玉田,马新谋,马昀. 履带式自行火炮负重轮轮毂轻量化技术研究[J]. 火炮发射与控制学报, 2009(2): 41-44.

PAN Yu-tian, MA Xin-mou, MA Yun. Lightweight technology study of tracked self-propelled gun bogie wheel hub[J]. Journal of Gun Launch & Control, 2009(2): 41-44.

[3] 张海航,于存贵,唐明晶. 某火炮上架结构拓扑优化设计[J]. 弹道学报,2009, 21(2): 83-85.

ZHANG Hai-hang, YU Cun-gui, TANG Ming-jing. Topological optimization design for the upper carriage of a gun [J]. Journal of Ballistics, 2009, 21(2): 83-85.

[4] 孙全兆,杨国来,葛建立. 某火炮上架结构改进设计[J]. 兵工学报,2012,33(11): 1281-1285.

SUN Quan-zhao, YANG Guo-lai,GE Jian-li. Improved design for top carriage of a gun[J].Acta Armamentarii,2012,33(11):1281-1285.

[5] 郑玲,唐重才,韩志明,等. 车身结构阻尼材料减振降噪优化设计[J]. 振动与冲击, 2015, 34(9): 42-47.

ZHENG Ling, TANG Zhong-cai, HAN Zhi-ming, et al. Optimal design of damping material to suppress interior noise in vehicle[J].Journal of Vibration and Shock,2015,34(9):42-47.

[6] 石海军,钱林方,徐亚栋,等.火炮卡膛一致性问题研究[J]. 弹道学报, 2012, 24(4): 77-81.

SHI Hai-jun, QIAN Lin-fang, XU Ya-dong, et al. Research on consistency of bayonet-chamber of gun[J]. Journal of Ballistics, 2012, 24(4): 77-81.

[7] 蒋清山,钱林方,邹权. 液压弹射输弹过程分析与参数优化[J]. 振动与冲击, 2015, 34(15): 98-102.

JIANG Qing-shan, QIAN Lin-fang, ZOU Quan. Analysis of hydraulic ejection ramming and parameter optimization[J]. Journal of Vibration and Shock, 2015, 34(15): 98-102.

[8] Ham F M,Kostanic I. Principles of neurocomputing for science and engineering [M]. NewYork: McGraw-Hill, 2001.

[9] 余衍然,李成,姚林泉,等. 基于傅里叶幅值检验扩展法的轨道车辆垂向模型全局灵敏度分析[J]. 振动与冲击, 2014, 33(6): 77-81.

YU Yan-ran, LI Cheng, YAO Lin-quan, et al. Global sensitivity analysis on vertical model of railway vehicle based on extended Fourier amplitude sensitivity test [J]. Journal of Vibration and Shock, 2014, 33(6): 77-81.

Lightweight design of an auto loading mechanism based on global sensitivity analysis

JIANGQing-shan,QIANLin-fang,CHENGuang-song

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:An optimization strategy composed of a global sensitive analysis method and the surrogate model technology was proposed for the case of large scale parameters and expensive computing cost in the lightweight design of an auto loading system. A global sensitive analysis based on Morris trajectory was carried out to determine the 14 important parameters from 32 ones. Simulations were performed on the Latin Hypercube Sampling points of important parameters, and the surrogate model of the responses about the important parameters was established based on RBF NN (radial basis function neural networks). The optimal lightweight solution was obtained by using the Multi-island Genetic Algorithm, with which the weight of the loading mechanism was reduced by 21.8%. A numerical example shows that the surrogate model including only the important parameters can achieve more accurate prediction results. The optimization strategy was proved to be efficient in the lightweight design of complex systems.

Key words:auto loading; global sensitivity analysis; lightweight design; parameter optimization

中图分类号:TJ301

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.06.007

通信作者钱林方 男，教授，博士生导师，1961年12月生

收稿日期：2015-06-10修改稿收到日期：2015-10-12

基金项目：国防基础科研(2620133003)

第一作者 蒋清山 男，博士生，1986年10月生