深入探究反思，提升数学思维品质

杨宪立,李冬辉

(河南教育学院 数学与统计学院,河南 郑州 450046)



深入探究反思，提升数学思维品质

杨宪立,李冬辉

(河南教育学院 数学与统计学院,河南 郑州 450046)

摘要：通过延长与截取的不同形式给出了一道联赛题的10种证明方法，探究变形与推广，改编了8个新的命题，并通过反思探究，从几何的角度得出了12个三角函数关系式.

关键词：探索性学习；数学思维；反思

探究性学习是新课标提倡的一种新型的学习方式.而适时地进行反思回顾则是有效提高数学解题能力、减轻学生作业负担的重要方法与手段.因此在数学教学过程中，要有目的地指导学生开展以“自主、合作、探究反思”为特征的学习方式，要让学生感受、理解知识产生的发展过程，实现“三位一体”的教学目标，有效培养学生的创造性思维，提升数学品质.

1深入探究问题的多种证法，培养思维的灵活性

对于一个题目，寻求多种证法，既能广开思路，培养学生数学思维的灵活性，又能帮助学生加深对问题的认识.因为不同的证法，往往是从不同的侧面反映出条件与结论之间的联系.

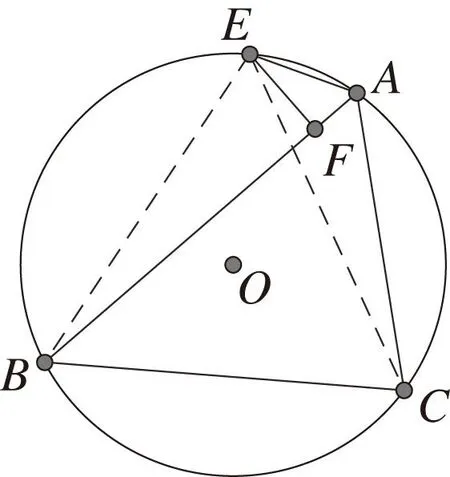
图1　例1图Fig.1　Example 1

例1如图1，在△ABC中，已知AB>AC,∠A的外角平分线交△ABC的外接圆于E，过E作EF⊥AB于F,求证：2AF=AB-AC(1989年全国联赛第二试第1题)[1].

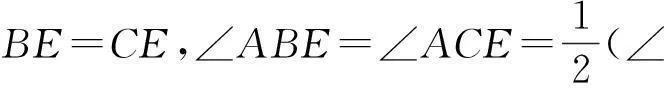
其次，观察问题的结论有哪些变式：

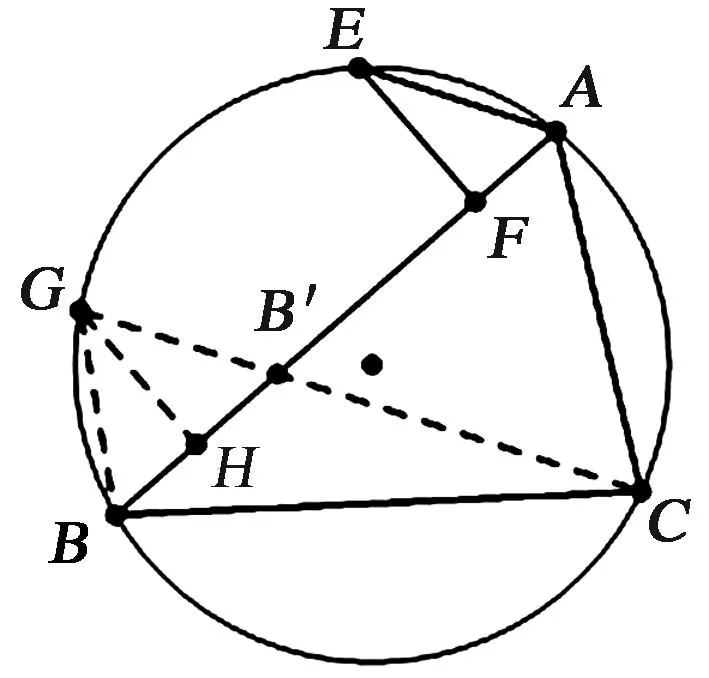
图2　证明1图Fig.2　Proof 1

①2AF=AB-AC⟺②AC=AB-2AF⟺③AB=AC+2AF⟺④AC+AF=AB-AF⟺⑤BF=AC+AF⟺⑥BF-AF=AC.

再次，反思回顾问题证明的基本思路.证明线段的和差相等的基本思路是：

(1)截取或延长；(2)直接运用相应的定理、例题；(3)计算.

证明1作差AB-AC.在AB上截取AB′=AC,则只需证明BB′=2AF，为此联结CB′并延长交外接圆于G,再作GH⊥AB于H,如图2.则有∠GBB′=∠GCA=∠AB′C=∠GB′B⟹BB′=2BH.

又，∠BCG=∠BCB′=∠AB′C-∠B=∠ACB′-∠B=∠C-∠BCB′-∠B.

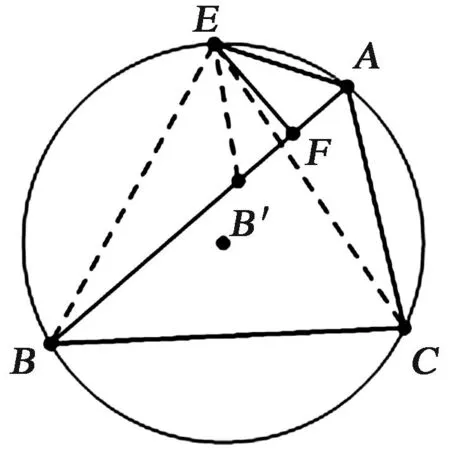
图3　证明2图Fig.3　Proof 2

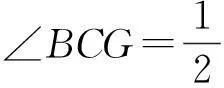
所以，RtΔGBH≅RtΔEAF，所以，BH=AF⟹BB′=2AF.

反思 可以在AB上作差，也可以在BA上作差，由此得证明2.

证明2作差BA-AC.在BA上截取BB′=AC,联结B′E,BE,CE，如图3，则有BE=CE,∠EBB′=∠ECA,BB′=CA，所以，ΔEBB′≅ΔECA⟹EB′=EA.又，EF⊥AB′，所以，AB′=2AF.

图4　证明3图Fig.4　Proof 3

考察第②个等价结论及基本思路，又有如下证明.

证明3作差AB-2AF.在AB上截取AA′=2AF,联结EA′,BE,CE,如图4，则有AA′=2AF,∠EA′A=∠EAA′,BE=CE.

∠EBA′=∠ECA,∠BA′E=π-∠EA′A=π-∠EAA′=∠CAE,所以，ΔBEA′≅ΔCEA，所以，BA′=CA.

考察第③个等价式子及基本思路——延长，可得如下3种证法.

证明4作和AC+2AF.延长AC至C′，使得AC′=AB，联结C′B交外接圆于G,联结GC,过G作GH⊥CC′于H，如图5，则有∠C′=∠ABC′=∠GCC′，所以，CC′=2CH.

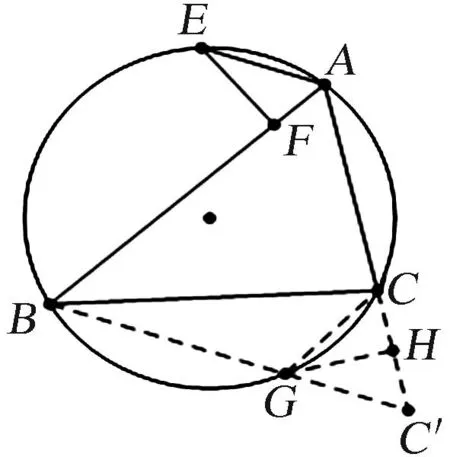
图5　证明4图Fig.5　Proof 4

又∠B+∠CBG=∠C′=∠C-∠CBG.

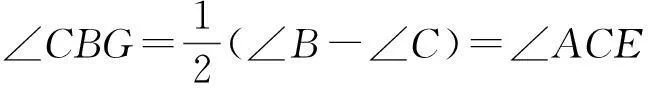
反思延长有两个方向，不同的方法，从而还有如下两种证法.

图6　证明5、6图Fig.6　Proofs 5、6

证明5作和CA+2AF.延长CA至A′使得CA′=BA，联结EA′,BE,CE，过E作EH⊥AA′于H,如图6，则有BE=CE,∠EBA=∠ECA′，所以，ΔABE≅ΔA′CE,所以，EA′=EA，∠EA′H=∠EAF，所以，RtΔEA′H≅RtΔEAF，所以，A′H=AH,AA′=2AF.

证明6作和CA+2AF.延长CA至A′，使得AA′=2AF，设H为AA′的中点，联结EH,EA′,BE,CE,如图6，则有AH=AF,∠EAF=∠EAH,EA=EA，所以，ΔEAF≅ΔEAH,所以，EH⊥AA′⟹ΔEAA′为等腰.又BE=CE,∠EBA=∠ECA′，∠EAB=∠EAA′=∠EA′C，所以，ΔEBA≅ΔECA′，所以，A′C=AB.

考察第④个等价式子,又有如下类似证法.

证明7作AC+AF.延长CA至D，使得CD=BF,联结BE,CE,DE,如图7，则有BE=CE,∠EBF=∠ECD,所以，ΔEBF≅ΔECD,所以，ED=EF,∠EDC=∠EFB=90°且EA=EA，所以，RtΔEAF≅RtΔEAD,所以，AD=AF.

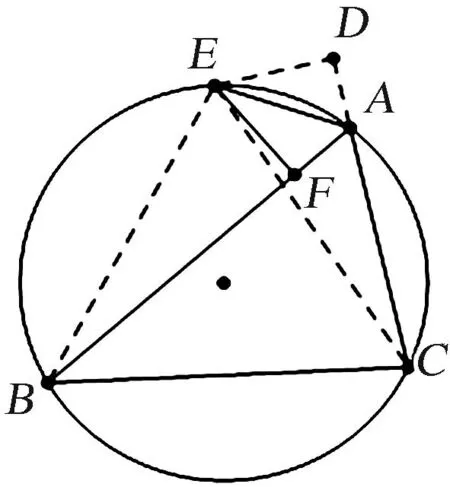
图7　证明7图Fig.7　Proof 7

注：也可延长CA至D，使得AD=AF.先证ΔEAD≅ΔEAF，再证RtΔEBF≅RtΔECD即可.

证明8作和FA+AC.延长FA至D使得AD=AC,联结BE,CE,DE,如图8，则有∠DAE=π-∠EAB=∠EAC,且EA=EA，所以，ΔEAD≅ΔEAC，所以，ED=EC=EB，且EF⊥BD.

所以，BF=FD.

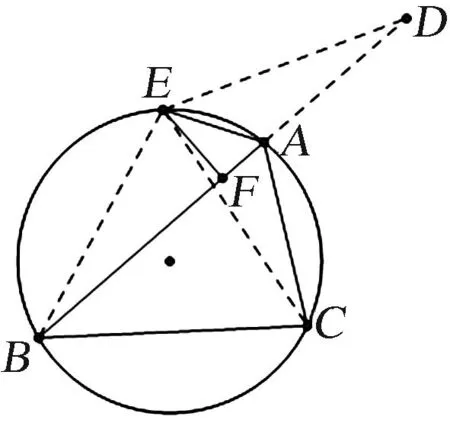
图8　证明8图Fig.8　Proof 8

注：也可延长FA至D使得FD=BF,而后证明AD=AC.

证明9作差BF-AF.在BF上截取BH=AF,过H作HG⊥BF交外接圆于G,联结BG,EG,BE,CE,如图9，则有BE=CE,EG//=FH,BG=AE,∠BEG=∠EBA=∠ACE,∠BGE=π-∠EAB=∠EAC.

所以，ΔBGE≅ΔEAC,所以，AC=GE=HF.

当难于找到几何证法时，不妨考虑运用正余弦定理进行计算.

证明10利用计算,如图10.令∠EAB=∠ECB=α,∠ACE=∠ABE=β，则由正弦定理得，AE=2Rsinβ,BE=2Rsinα,AC=2Rsin(α-β).

图9　证明9图Fig.9　Proof 9

所以，BF=BEcosβ=2Rsinαcosβ，AF=AEcosα=2Rsinβcosα.

所以，AC+AF=2Rsin(α-β)+2Rsinβcosα=2Rsinαcosβ=BF.

2探究问题的变形推广，培养思维的深刻性

任何一个命题都有逆命题，但一个命题的逆命题却不一定是真命题.这就启发我们把一些命题作为原命题，然后去探究它的逆命题，如果逆命题成立，那么就得到一个新的命题.

由于本命题的条件与结论都是唯一的，所以逆命题是成立的，由此得逆命题：

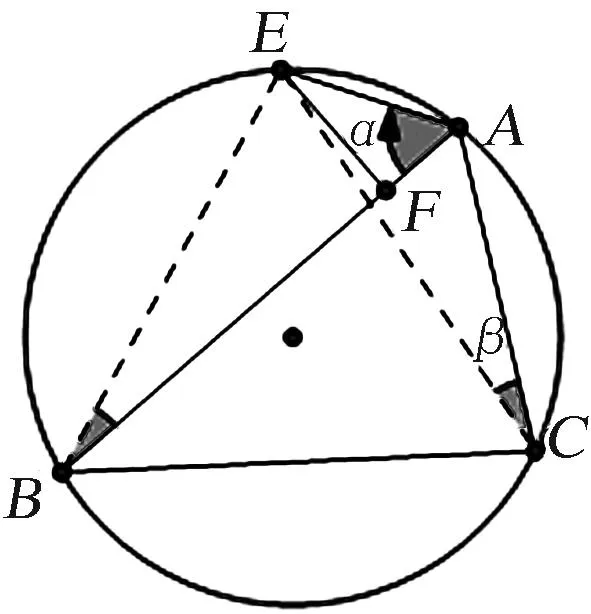
图10　证明10图Fig.10　Proof 10

命题1已知在△ABC中，AB>AC,∠A的外角平分线交△ABC的外接圆于E，F为AB上一点,且BF=AC+AF,求证：EF⊥AB.

命题2已知在△ABC中，AB>AC,F为AB上一点，且BF=AC+AF,过F作FE⊥AB交△ABC的外接圆于E，求证：AE为∠A的外角平分线或点E为BAC弧的中点.

2.2探究命题结论的多样性

如果根据题设条件，可以得到几个不同的结论，那么，每个结论都是一个新的命题.

由AB-AC=2AF,得AB-AF=AC+AF,或BF=AC+AF,把∠A的外角平分线与△ABC的外接圆交于E修改为E为BAC弧的中点，则得著名的折弦(阿基米德)定理：

命题3[2]如果AB和AC组成一条圆O的折弦(AB>AC),E为BAC弧的中点，过E作EF⊥AB于F，则BF=AC+AF.

从广州出发飞 行了16个小时，再坐上2小时的大巴，穿越一片片平坦开阔的葡萄园、橄榄园，路过一栋栋白色或浅黄色的石屋，终于抵达普利亚产区的中心城市：曼杜里亚。此时接近正午，阳光正好，清劲的海风扑面而来，一下子驱散了长途旅行的不适。空气中弥漫着橄榄香、泥土香，暖暖的，非常惬意。放眼望去，都是狭窄的石头街道、古老的石头房子和教堂，街上行人寥寥。

又由于BF-AF=AC,BF+AF=AB，所以，BF2-AF2=AB·AC,而BF2=BE2-EF2,AF2=AE2-EF2，所以，BE2-AE2=AB·AC，故有以下命题4：

命题4已知在△ABC中，AB>AC,∠A的外角平分线交△ABC的外接圆于E，求证：BE2-AE2=AB·AC.

2.3探究改变命题

对一些数学命题，认真分析其条件与结论中的本质特征，然后以命题条件或结论中的本质特征为龙头，对原命题中的一些非本质的条件进行修正、移植，也可得到一些有益的命题.

E是∠A的外角平分线与△ABC的外接圆的交点，实质就是EB=EC，或△EBC为等腰三角形，为此可改编为

命题5已知等腰△EBC，EB=EC，A为△EBC外接圆CE弧上任意一点，EF⊥AB于F，则AB-AC=2AF.

由EB=EC，可知E在BC的中垂线上，为此又可改编为

命题6已知在△ABC中，AB>AC,BC的中垂线交△ABC的外接圆于E，过E作EF⊥AB于F,求证：2AF=AB-AC.

结合命题4，又有

命题7[3]已知在△ABC中，AB>AC,BC的中垂线交△ABC的外接圆于E，求证：BE2-AE2=AB·AC.

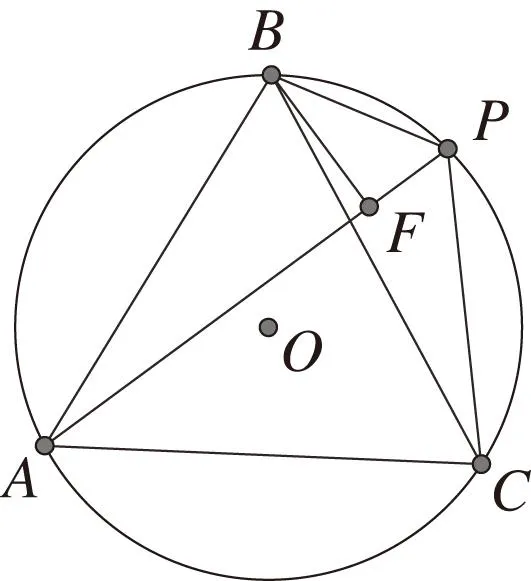
图11　命题8图Fig.11　Proposition 8

2.4探究命题的特殊情形

对某些数学命题，可观察其极端情形、特殊情形而构造新的命题.

在命题的条件下，将等腰△EBC特殊化为正三角形，则有∠EAB=∠ECB=60°，所以AE=2AF,AC+AE=AB,从而得命题：

命题8[4]如图11，已知P为正△ABC的外接圆BC弧上一点， 求证：①PA=PB+PC；②PA2+PB2+PC2=2BC2.

由此可见，在数学教学中，适时地指导学生对一些命题进行探究改编，对提高学生学习数学的兴趣，培养学生数学思维的深刻性具有重要的意义.

3反思回顾，培养思维的创造性

反思第10种计算方法，能从证明中得到什么呢？若已证明BF=AC+AF，则有AC=BF-AF,即

2Rsin(α-β)=2Rsinαcosβ-2Rcosαsinβ，

或

sin(α-β)=sinαcosβ-cosαsinβ.

(1)

这是两角差的正弦三角函数公式——由一个几何问题推出来了.由图中的几何线段相等，还能推出其他公式吗？为了方便，且不失一般性，设圆O的直径为1，即2R=1，则根据正弦定理与锐角三角函数定义，有

反思1由AF+BF=AB，BF=sinαcosβ，AF=sinβcosα，AB=sin(α+β)，得

sin(α+β)=sinαcosβ+cosαsinβ.

(2)

反思2图12，设BC的中点为G，则有BC=2BG，BG=BEcosα=sinαcosα，BC=sin∠BEC=sin(π-2α)=sin 2α，所以

sin 2α=2 sinαcosα.

(3)

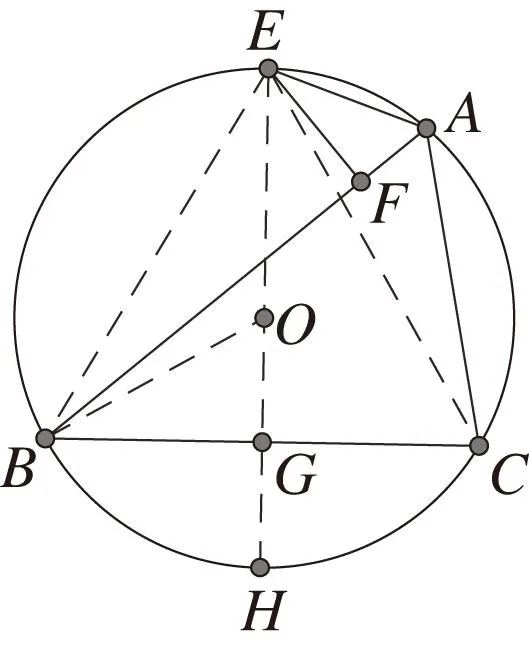
图12　反思2、3图Fig.12　Reflections 2、3

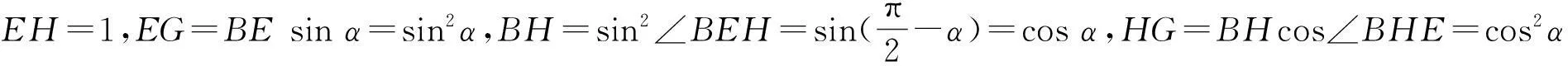
sin2α+cos2α=1.

(4)

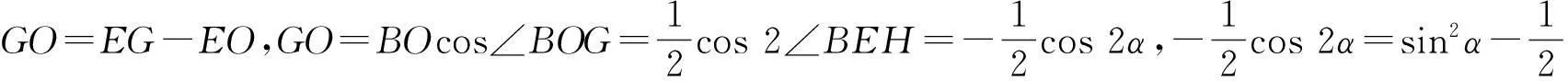
cos 2α=1-2sin2α.

(5)

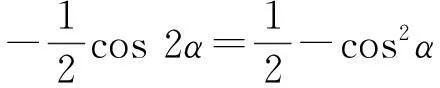
cos 2α=2cos2α-1.

(6)

反思6由AB-AC=2AF，得2cosαsinβ=sin(α+β)-sin(α-β)，即

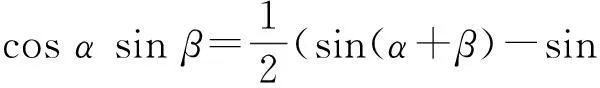
(7)

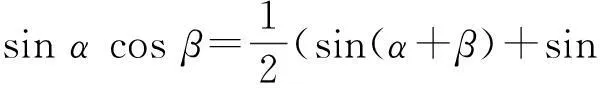
(8)

至此，已得到8个三角函数公式，继续观察图形，进行深入反思探究，延长EF交外接圆于K,如图13，则有EK=EF+FK,为此有

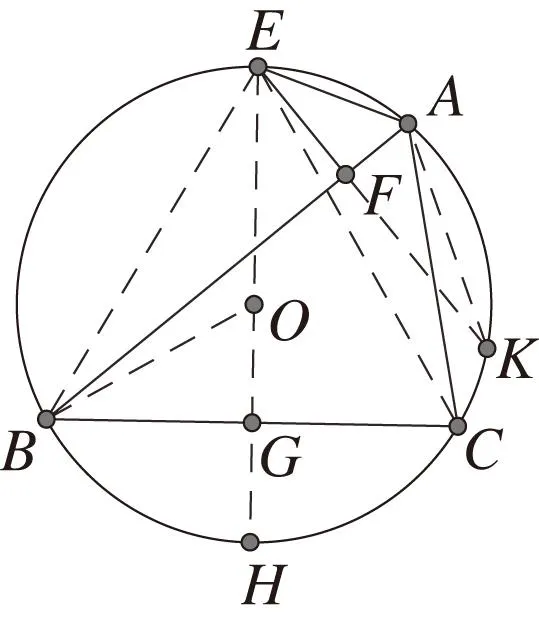
图13　反思8图Fig.13　Reflection 8

反思8由于∠ECK=∠ECA+∠ACK=β+∠AEK=β+90°-α，所以EK=sin(90°+β-α)=cos(α-β)，EF=AEsinα=sinαsinβ，AK=sin∠ACK=sin∠AEK=sin(90°-α)=cosα.

所以FK=AKcos∠AKF=cosαcosβ,再由EK=EF+FK，得

cos(α-β)=cosαcosβ+sinαsinβ.

(9)

对于常用的三角函数基本公式，只剩下了两角和的余弦公式，为了求cos(α+β)，继续深入反思：由于我们已知cos(α+β)=cosαcosβ-sinαsinβ及EF=sinαsinβ，FK=cosαcosβ,为此作E关于AB的对称点E′，如图14，则只需验证E′K=FK-EF=cos(α+β)即可.

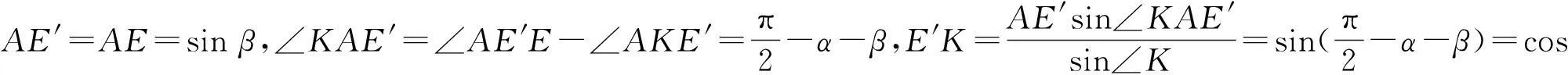
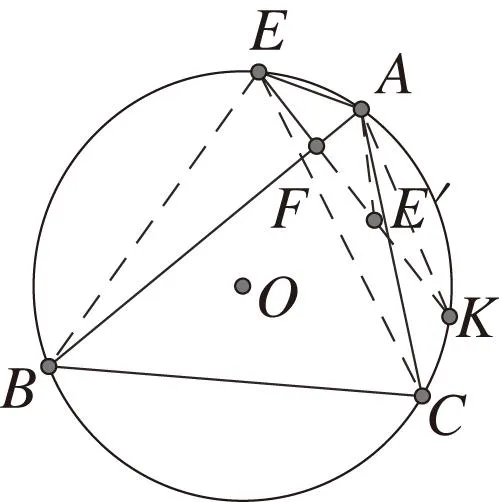
图14　反思9图Fig.14　Reflection 9

由E′K=FK-FE′，得

cos(α+β)=cosαcosβ-sinαsinβ.

(10)

由EK-E′K=EE′=2EF，得

cos(α-β)-cos(α+β)=2 sinαsinβ.

(11)

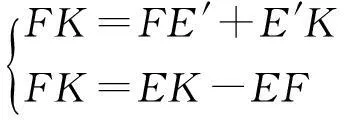
2 cosαcosβ=cos(α-β)+cos(α+β).

(12)

至此，推出了12个三角函数公式.这使我们深深体会到，反思便于拓宽解题思路，反思使学生对知识会有更深刻的理解；只要深入反思探究,或多或少都会得到一些意外的收获，尝到发现公式(新知识)的乐趣，而且对自己的发现终身难忘，或许由此便喜欢上了数学[2].

参考文献

[1]李长明，周焕山.初等数学研究[M].北京：高等教育出版社，2005：391.

[2]杨宪立，杨之. 折弦定理——研究性学习的一个好课题[J].数学通报，2011(4)：19-20.

[3]闫照林，韩友信，闫雪.阿基米德折弦定理及其应用[J].中学数学月刊，1997(6)：33-35.

[4]朱德祥.初等几何研究[M].北京：高等教育出版社，1994:37.

Further Explore and Reflect, Improve the Quality of Mathematics Thinking

YANG Xianli, LI Donghui

(SchoolofMathematicsandStatistics,HenanInstituteofEducation,Zhengzhou450046,China)

Abstract:Puts forward ten kinds of proof method of a contest problem by different forms of extending and interception, makes an inquiry into the deformation and generalization, and adapts eight new propositions. With reflection and exploration, twelve kinds of trigonometric function relationship are proposed, which are based on the perspective of geometry.

Key words:exploring study; mathematics thinking; reflection

中图分类号：G642.0

文献标志码：A

文章编号：1007-0834(2016)01-0053-05

doi：10.3969/j.issn.1007-0834.2016.01.012

作者简介：杨宪立(1961—)，男，河南林州人，河南教育学院数学与统计学院副教授，主要研究方向：数学教育.

基金项目：河南省教育厅教师教育课程改革研究项目(2015-JSJYYB-120)

收稿日期：2015-11-05