对称性方法在谐振子模型教学中的应用

夏丽莉

(河南教育学院 物理与电子工程学院，河南 郑州 450046 )



对称性方法在谐振子模型教学中的应用

夏丽莉

(河南教育学院 物理与电子工程学院，河南 郑州 450046 )

摘要：利用对称性方法探索非线性谐振子的物理特性.给出一种简洁实用的探究系统守恒律的现代数学方法.有利于学生更深入地了解机械振动模型的规律，丰富了教材内容.

关键词：谐振子模型；对称性方法；守恒律

0引言

谐振子模型是讲述机械振动内容时引入的一种典型的非线性动力学模型.这个模型设计简单，能比较完整地体现简谐振动的物理特征，被国内大多数物理学教材广泛采用. 在教师的教授和学生的学习过程中，谐振子模型的引入使“教”与“学”都取得了较好的效果. 谐振子模型的重要性不仅体现在理论层面上，自然界中的简谐运动等物理现象都可以看成谐振子模型.非线性谐振子是经典力学、量子力学、相对论力学中备受关注的问题，研究非线性谐振子模型的性质具有重要的理论意义.通过对谐振子运动的研究，不仅能了解周期性物理现象的本质，更能发现与周期性相关及影响周期性运动的物理现象，如能量守恒原理、孤立系统、耗散系统以及混沌等现代物理概念.这也是很多教师在教材内容和教学方法上同时注重研究谐振子模型的原因[1-2]. 对于非线性谐振子的研究内容，很多教材中都是通过将非线性因素简化为线性项，再由给定的初始条件，求得线性系统的解析解，利用解析结果分析非线性谐振子的性质.教材[3]从系统机械能守恒出发，给出了关于角坐标和角速度的一阶微分方程，将初始能量取值分为3种情况，得出相应的角坐标和周期的近似解析表达式.本文立足于用新的解题技巧处理更一般化的物理问题，对大家熟知的谐振子模型，用对称性方法探索其物理性质，丰富了教学内容，开阔了学生视野，使学生对物理学中具有重要地位的对称性概念和作用有更深刻和直观的认识.

1非线性谐振子方程

在讲述简谐振动的动力学特征时，通常引入单摆的模型作为简谐振动的例子，用不可伸长的细线悬挂一个小球，将小球视为质点，它受重力和悬线拉力的合力作用，质点在竖直面内沿圆弧摆动，摆动中相对于悬线竖直位置夹角为θ. 非线性谐振子微分方程可表示为

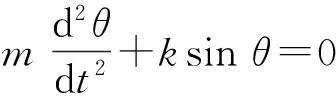
(1)

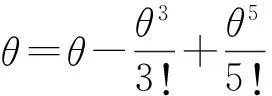
假设方程(1)有能量积分

(2)

有解

(3)

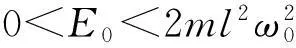
(4)

由于这些近似解析解中存在第一类椭圆积分，所以用其解来分析系统的物理特性有一定的难度. 可以构造系统的拉格朗日函数，从拉格朗日方程出发，根据诺特定理，得到系统的积分，进而体现非线性谐振子的物理特征.

2系统的守恒定律

非线性谐振子的典型物理特征就是具有能量守恒的结论. 如果探索更加复杂的非线性模型的物理属性，结论不会这样显而易见. 利用近似解析解来达到目的显然是不合适的. 对于非线性物理模型，利用诺特对称性理论求得系统相应的积分成为人们近年来探求守恒律的主要途径. 对谐振子的对称性理论，国内外学者做了一定的研究工作[5-6]. 诺特对称性是基于哈密顿作用量在无限小群变换下的不变性，所以先将系统方程表示为欧拉-拉格朗日方程的形式. 引入时间和广义坐标的无限小变换，利用诺特对称性定理，可以得到系统的守恒律表达式. 下面给出保守力学系统的诺特定理.

首先引入广义坐标的概念，在研究过程中，凡是能够确定系统位置的、适当选取的独立变量即称为广义坐标. 广义坐标可以是距离、角度、面积等物理量,所以相对于直角坐标意义更加广泛. 对于非线性谐振子系统的直角坐标中的角度和时间量，可以用广义坐标qs和时间t表示. 根据达朗贝尔-拉格朗日原理、虚位移定义和两个经典的拉格朗日关系，在保守系统中，可以得到其欧拉-拉格朗日方程，即对于质点系, 质点的质量为mi(i=1,…,N), 系统的位形由n个广义坐标qs(s=1,2，…,n)确定.系统的运动微分方程可以表示为Routh形式[7]

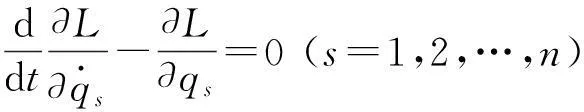
(5)

其中L=T-V为系统的拉格朗日函数.

引入时间和广义坐标的无限小变换

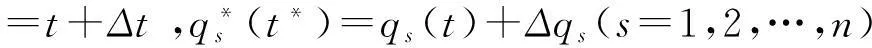
(6)

其中为ε无限小参数,τ,ξs为无限小生成元.

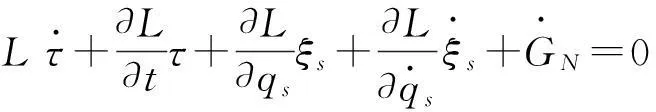
(7)

则相应对称性为完整力学系统的诺特对称性.

保守力学系统的诺特对称性可得到诺特守恒量.

定理1对于保守力学系统,诺特对称性可导致诺特守恒量

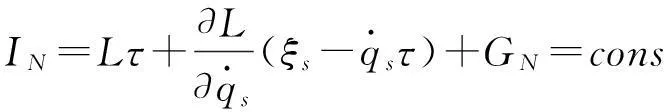
(8)

证明等式(8)式对时间求一阶导

(9)

由(7)式可得

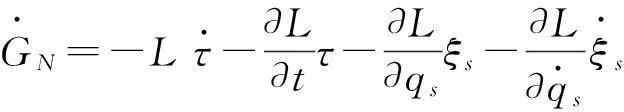
(10)

基于诺特定理，可以研究非线性谐振子系统的相关性质. 非线性谐振子的运动方程可表示为

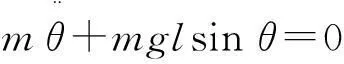
(11)

非线性谐振子拉格朗日函数为

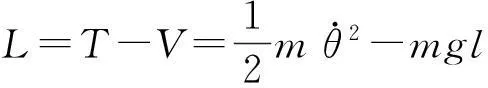
(12)

这里T为系统的动能，V为系统的势能. 诺特等式(7)给出

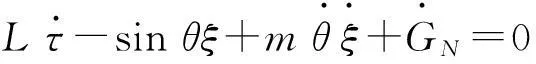
(13)

方程(8)的解为τ=1，ξ=0，GN=0. 由诺特定理，得守恒量

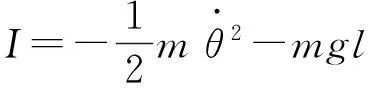
(14)

系统的能量守恒，也就是说，若拉格朗日函数不显含时间，且仅作时间平移变换，可以得到广义能量积分. 守恒律(14)式是通过诺特定理得到的，这和教材中给出的结论是一致的. 这种方法在处理类似的非线性问题时简洁而有效，教学过程中，需要向学生引入广义坐标的概念和拉格朗日函数的物理意义. 这是顺利引入对称性方法的前提.

3总结

在简谐振动的教学中，学生对线性谐振子模型比较熟悉，也容易掌握其运动规律. 但是对于更一般的非线性谐振子模型，不能顺利得到谐振子方程的解，通过引入广义坐标和拉格朗日函数的知识点，由系统的对称性和守恒量理论同样可以求得系统的能量守恒律. 这种方法没有直接给出系统微分方程的解，却可以得到系统的守恒律. 在教学过程中，当有类似的非线性方程出现时，可以用对称性理论处理. 对称性理论的引入，一方面，对教材建设而言，体现了对称性理论在物理教学中的重要性，丰富了教材内容；另一方面，对学生的发展而言，扩展了学生的知识面，使学生对简谐振动的内容有了更加深入的认识.

参考文献

[1]漆安慎，杜婵英. 力学[M]. 北京：高等教育出版社，2005:285.

[2]舒幼生. 力学[M]. 北京：北京大学出版社，2005:240.

[3]梁昆淼. 力学[M]. 北京：高等教育出版社，2004:74.

[4]梅凤祥，尚枚. 理论力学：II[M]. 北京：高等教育出版社，2012:58.

[5]CALOGERO F. On the quatization of yet another two nonlinear harmonic oscillators[J]. Journal of Nonlinear Mathmatical Physics, 2004, 11(1): 1-6.

[6]楼智美, 梅凤翔. 二维各向异性谐振子的第三个独立守恒量及其对称性[J]. 物理学报, 2012, 61(11): 110201.

[7]梅凤翔, 尚枚. 理论力学：I[M]. 北京：高等教育出版社, 2012:458.

Applications of Symmetry Method in Teaching of Harmonic Oscillator Model

XIA Lili

(InstituteofPhysicsandElectronicEngineering，HenanInstituteofEducation，Zhengzhou450046，China)

Abstract:The physical properties of the harmonic oscillator are obtained by the symmetry method. The modern mathematical methods of exploring the conserved quantities are proposed. This will help the students to understand the laws of the harmonic oscillator model, and enrich the teaching materials.

Key words:harmonic oscillator model; symmetry method; conserved quantities

中图分类号：G642.0

文献标志码：A

文章编号：1007-0834(2016)01-0070-03

doi：10.3969/j.issn.1007-0834.2016.01.016

作者简介：夏丽莉(1980—)女，江苏徐州人，河南教育学院物理与电子工程学院讲师，博士，主要研究方向：动力学系统的可积性理论、物理学教育教学.

基金项目：国家自然科学基金青年科学基金(11502071)

收稿日期：2015-11-08