利用四则运算法则求极限易错题分析

景慧丽

(火箭军工程大学 理学院，陕西 西安 710025)



利用四则运算法则求极限易错题分析

景慧丽

(火箭军工程大学 理学院，陕西 西安 710025)

摘要：利用极限的四则运算法则求极限是一种最基本的方法.把解题过程中经常出现的错误进行总结，发现常见的错误类型有3种：一是忽视极限存在这个前提，二是忽视有限项这个前提，三是忽视分母的极限不能为零这个前提.就每种错误给出了相应的例题，对错解进行分析，最后给出了正确解法.

关键词：极限；四则运算法则；易错题；分析

极限思想是微积分学中最重要的思想之一，在微积分学中求极限的方法有很多，如利用极限的四则运算法则、利用等价无穷小代换、利用两个重要极限、利用洛比达法则等，每种方法也都有自己的使用条件和适用范围.极限的四则运算法则是最基本的也是最常用的求极限的方法，很多求极限题目最终的一个步骤运用的都是极限的四则运算法则，因此极限的四则运算法则是非常重要的.但笔者在教学中发现，学员在使用四则运算法则求极限时经常出错，而且不管是否满足四则运算法则的使用条件就直接利用该法则.

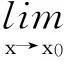
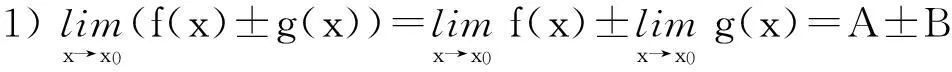
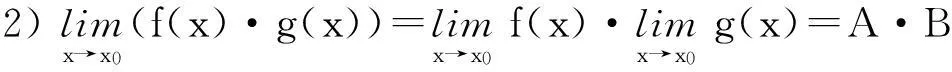
极限四则运算法则的结论1)和2)可以推广到任意有限项，这里不再赘述.极限四则运算法则理解起来并不难，而且使用起来很方便，但是学员在使用时经常出错，其常见错误类型主要有以下3种.

1忽视“极限存在”这个前提

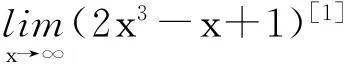
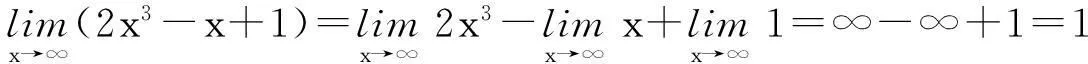
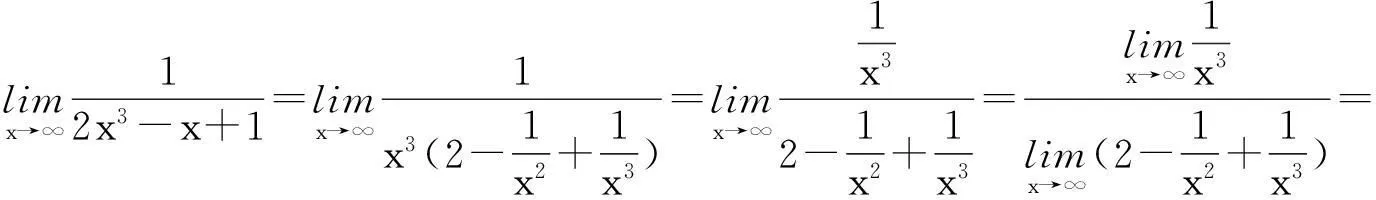
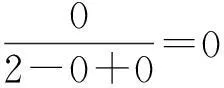
当然，如果两个函数(或数列)只有一个存在极限，另一个极限不存在，也是不能应用极限的四则运算法则的.

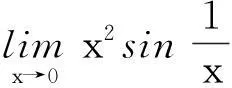
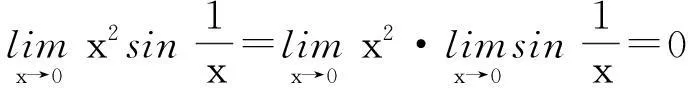
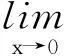
因此，在利用极限的四则运算法则求极限时，一定要满足其使用的前提条件，千万不能不管条件，随心所欲，否则就容易出错[2].

2忽视“有限项”这个前提

极限四则运算法则成立的另外一个重要前提是有限项，即有限个函数(或数列)相加减或相乘求极限时，才能应用极限的和、差或乘积来求极限，但大部分同学也往往忽略了“有限项”这个前提条件.

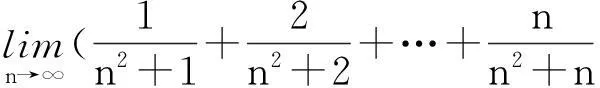
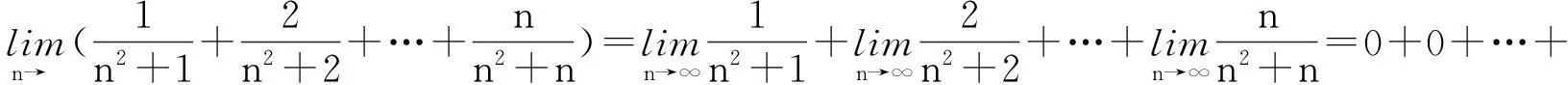
0=0.

分析上述解法错在

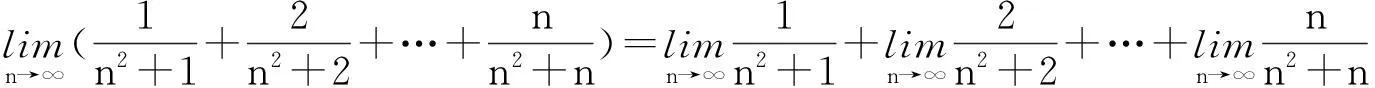
正解利用夹逼准则，即由于

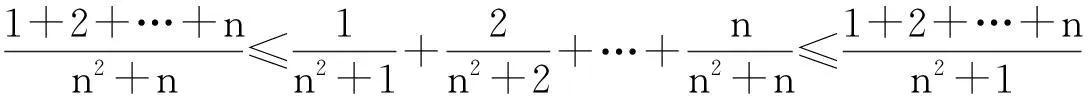
且

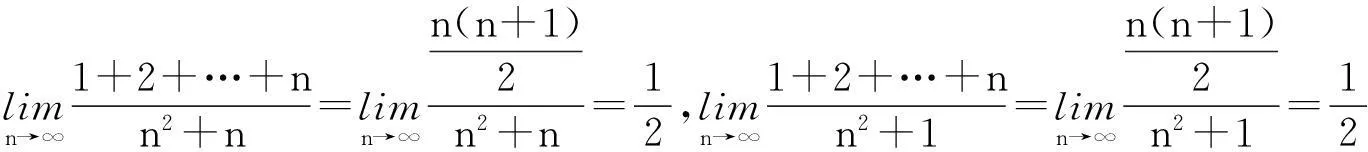
所以由夹逼准则得，

3忽视“分母的极限不能为零”这个前提

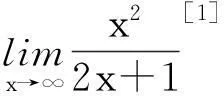
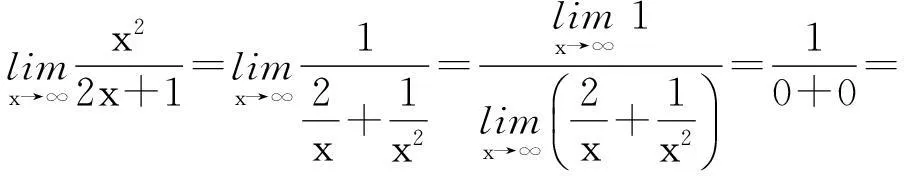
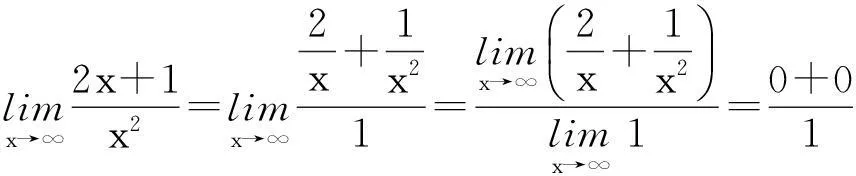
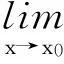
以上就是在利用极限的四则运算法则求极限时经常出现的错误，其实只要真正理解了极限的四则运算法则，上述错误是完全可以避免的.当然，也应正确看待这些“错题”资源，心理学家盖耶说过：“谁不考虑尝试错误，不允许学生犯错误，就将错过最富成效的学习时刻.”[3]在教学中要主动挖掘“错题”中的“闪光点”，及时进行探究、分析和讲评，培养学员的问题意识及发现问题、解决问题的能力[4].

参考文献

[1]同济大学应用数学系.高等数学：上[M].7版.北京：高等教育出版社,2014：39-45.

[2]景慧丽.极限求解方法研究[J].哈尔滨师范大学学报,2015(5)：16-17.

[3]钱怡杰.基于错题的高三基础会计教学探究[J].经营管理者,2015(2)：372-373.

[4]景慧丽.第二类曲面积分易错题分析研究[J].商丘职业技术学院学报,2015(5)：4-8.

Analysis on Easily Wrong Topic of Calculating Limits by Limit Laws

JING Huili

(SchoolofScience,RocketForceUniversityofEngineering,Xi’an710025,China)

Abstract:Using the limit laws to calculate limits is the basic method. The errors in the process of problem solving are concluded. There are three kinds of common errors: ignoring the existence of the limits, ignoring the finite terms and ignoring the denominator of the limit is not zero. Furthermore, some corresponding examples are given for each type of error, the wrong and correct solutions are analyzed.

Key words:limit laws； easily wrong topic； analysis

中图分类号：O172

文献标识码：A

文章编号：1007-0834(2016)01-0062-03

doi：10.3969/j.issn.1007-0834.2016.01.014

作者简介：景慧丽(1983—)，女，河南平顶山人，火箭军工程大学理学院讲师.

基金项目：火箭军工程大学教育教学立项课题(EPGC2015008)

收稿日期：2015-11-27