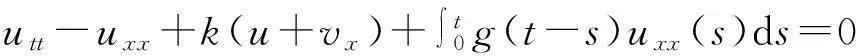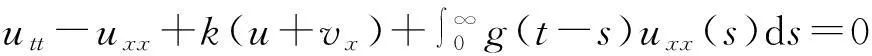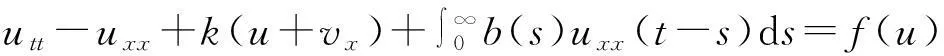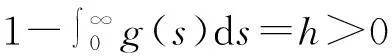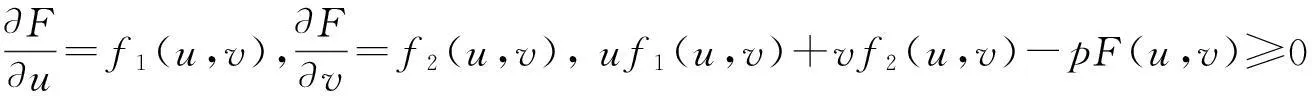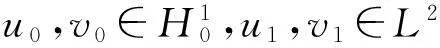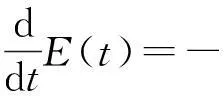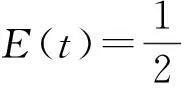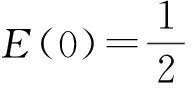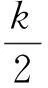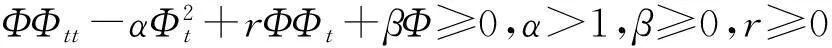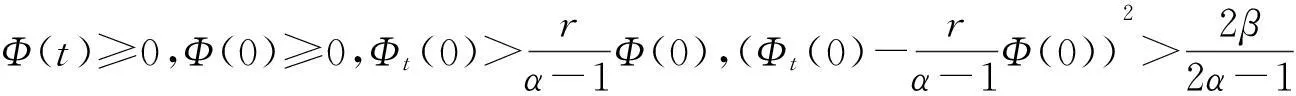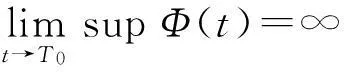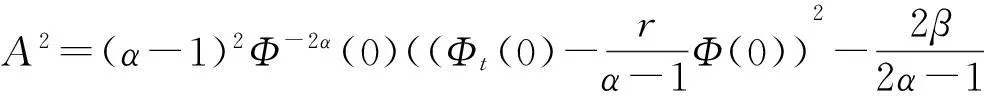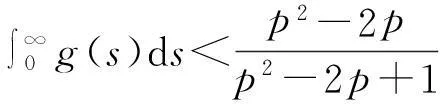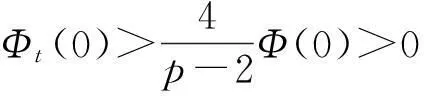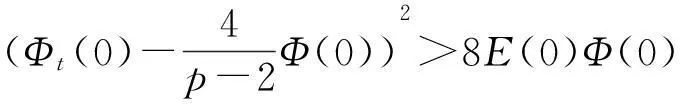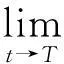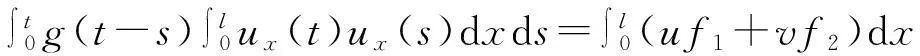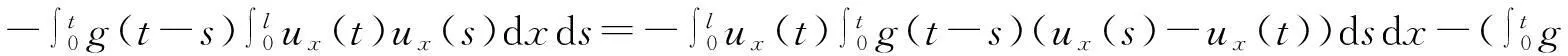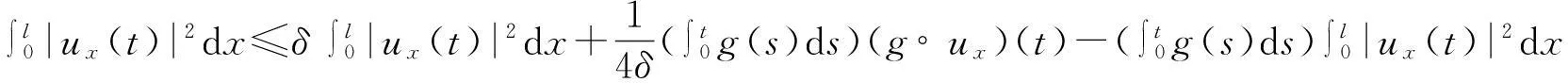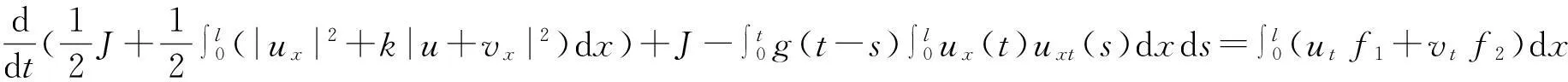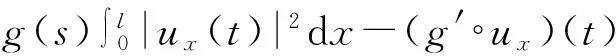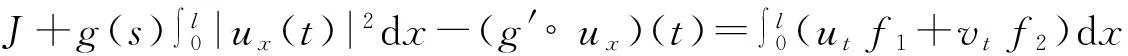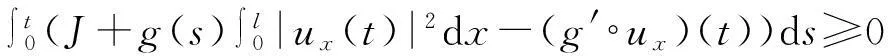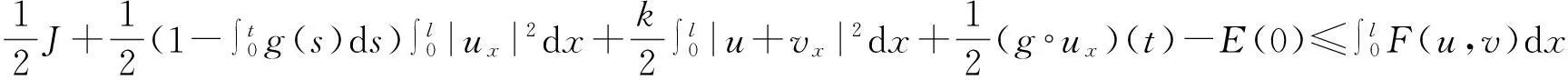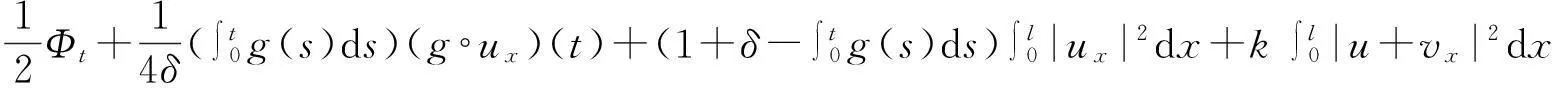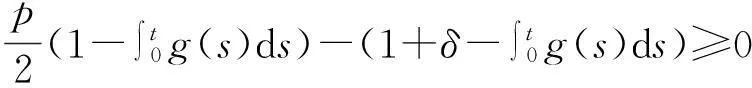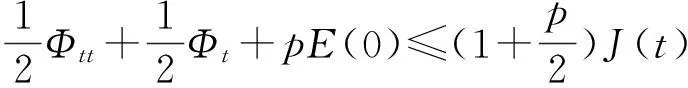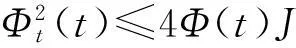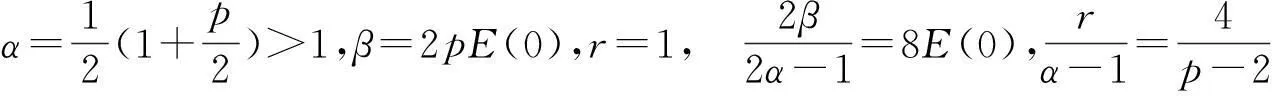具任意正初始能量的记忆Mindlin-Timoshenko梁方程解的爆破

闫德明， 张桂霞

(1.河南教育学院 数学与统计学院，河南 郑州 450046；2.三门峡市湖滨区中等职业教育学校，河南 三门峡 472002)



具任意正初始能量的记忆Mindlin-Timoshenko梁方程解的爆破

闫德明1， 张桂霞2

(1.河南教育学院 数学与统计学院，河南 郑州 450046；2.三门峡市湖滨区中等职业教育学校，河南 三门峡 472002)

摘要：研究了具记忆项的Mindlin-Timoshenko梁方程初边值问题解的爆破性．利用改进的凸性方法给出了具任意正初始能量和适当的初始条件下，Mindlin-Timoshenko梁方程初边值问题解的爆破性条件．

关键词：Mindlin-Timoshenko梁方程；初边值问题；记忆项；改进的凸性方法；爆破性

0引言

本文研究如下一类具记忆项的Mindlin-Timoshenko梁方程初边值问题解的爆破性，

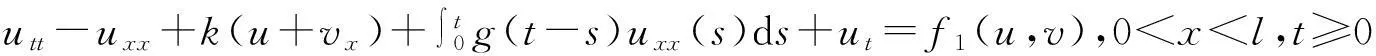
(1)

vtt-k(u+vx)x+vt=f2(u,v),0

(2)

u(0,t)=v(0,t)=u(l,t)=v(l,t)=0,t>0,

(3)

u(x,0)=u0(x),ut(x,0)=u1(x),0

(4)

v(x,0)=v0(x),vt(x,0)=v1(x),0

(5)

其中k>0为正常数，g是非负非增的记忆函数，u0,u1,v0,v1是给定的初始值，f1(u,v)，f2(u,v)是给定的非线性函数．当记忆函数g=0和无阻尼项且非线性函数f1(u,v)=f2(u,v)=0时，方程(1)、(2)就是著名的Mindlin-Timoshenko梁方程[1](或Timoshenko梁方程)，

utt-uxx+k(u+vx)=0，

(6)

vtt-k(u+vx)x=0,

(7)

其中t表示时间变量，x表示位置变量，v表示梁的横向位移,u是旋转角．由于它的广泛应用，在过去的几十年中，Timoshenko梁方程引起了人们的极大兴趣．方程(6)、(7)在各种边界条件下已经被许多数学家研究过,关于其解存在性和能量衰减性也已经有许多结果,这里不再列举．RAPOSO等[2]利用半群理论研究了齐次Dirichlet边界和两个线性摩擦阻尼的方程(6)、(7),即

utt-uxx+k(u+vx)+ut=0，

vtt-k(u+vx)x+vt=0,

得到了其能量指数衰减性. SOUFYANE和WEHBE[3]则利用局部分布反馈研究了下述问题，

utt-uxx+k(u+vx)+b(x)ut=0，

vtt-k(u+vx)x=0,

其中b(x)是正且有非零下界的连续函数,文献[3]给出了其一致稳定的充要条件. XU和YUNG[4]则对点点反馈利用特征值和特征函数得到了稳定性.AMMAR-KHODJA等[5]则考虑了具记忆项的Timoshenko系统

vtt-k(u+vx)x=0，

他们在齐次边界和g一致衰减情况下利用乘子技术得到了内一致稳定性. GUESMIA 和 MESSAOUDI[6]讨论了类似的情况. SANTOS[7]则讨论了类似的边界记忆反馈的稳定性. 最近, MESSAOUDI 和MUSTAFA[8]则对更一般的松弛函数改进了文献[5]和文献[6]的结果.此外,文献[9]和文献[10]还研究了具记忆历史的问题

vtt-k(u+vx)x=0.

对于半线性Timoshenko系统，PARENTE等[11]在f(u),g(v)满足局部Lipschitz连续条件下得到问题

utt-uxx+k(u+vx)+f(u)=0,

(8)

vtt-k(u+vx)x+g(v)=0,

(9)

解得存在唯一性．ARARUNA 等[12]研究了问题(8)，(9)还有边界阻尼时，利用Fadeo-Galerkin方法证明了问题强解和弱解的存在唯一性以及弱解的指数衰减估计．在多维情况下, CHUSEHOV和LASIECKA[13]研究了二维情况下f(u)，g(v)局部Lipschitz连续时，问题的紧整体吸引子的存在性．GORGI 和VEGNI[14]提出了如下Dirichlet 边界和记忆项时Timoshenko系统,

vtt-k(u+vx)x=g(v),

他们得到了解得衰减估计和吸收集的估计.

然而，据笔者所知，很少有人研究该类带有源项的Timoshenko系统解的不存在性．最近，PEI 等人[15]利用位势井理论研究了Reissner Mindlin-Timoshenko板系统解的整体适定性和长时间行为，他们主要聚焦于非线性阻尼项和源项的相互作用问题．

本文将研究带有记忆项和源项的Mindlin-Timoshenko系统整体解的不存在性．我们将利用源于LEVINE[16]的修正的凸性方法,该方法由KORPUSOV[17]提出并用于证明Klein-Gordon方程解的不存在性．本文将其用于带有记忆项和源项的Mindlin-Timoshenko系统．这时出现的困难是对记忆项的要求以及出现的范数‖u+vx‖如何处理，为此给出了g满足的一个不等式和一个等价不等式，从而证明了任意初始能量解的爆破问题．

1准备知识

本文对记忆函数g和非线性函数f1(u,v)，f2(u,v)假设如下:

H2)存在连续函数F(u,v)≥0以及常数p>2,使得对任意u,v∈R,有

H3) 存在常数d>2,使得对任意u,v∈R,有

|f1(u,v)|≤d(|u|m+|v|m),|f2(u,v)|≤d(|u|m+|v|m).

显然满足假设的函数g和非线性函数f1(u,v)，f2(u,v)是存在的.

其中

以及

最后，给出证明主要结论需要的引理．

引理1[17]假设Φ(t)∈C2([0,T))并满足如下不等式

(10)

(11)

2解的爆破

主要结论如下.

定理1设u是问题(1)～(5)的局部解, 假设H1)～H3)成立，

(12)

E(0)>0,

证明 记J(t)=‖ut‖2+‖vt‖2.方程(1)两边同乘u,方程(2)两边同乘v,二者相加后在[0,l]上积分,并利用分部积分得

(13)

注意到

其中δ>0，则(13)变为

(14)

类似地，方程(1)两边同乘ut,方程(2)两边同乘vt,二者相加后在[0,l]上积分,并利用分部积分得

(15)

注意到

则(15)变为

(16)

得

(17)

(14)结合(17)得

(18)

于是由(18)得不等式

(19)

又根据Cauchy-Schwartz不等式,

(20)

这时,时间T满足T≤Φ(2-p)/4(0)A-1且

(21)

其中

Φ(0)=‖u0‖2+‖v0‖2,Φt(0)=2(u0,u1)+2(v0,v1),

(22)

注:使得(21)和(22)成立的条件是能够保证的.

参考文献

[1]TIMOSHENKO S. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. Philosophical Magazine, 1921，41：744 - 746.

[2]RAPOSO C A, FERREIRA J, SANTOS M L, et al. Exponential stability for the Timoshenko system with two weak dampings[J]. Appl Math Lett, 2005，18: 535-541.

[3]SOUFYANE A, WEHBE A. Uniform stabilization for the Timoshenko beam by a locally distributed damping[J]. Electron J Differential Equations, 2003, 29: 1-14.

[4]XU G Q, YUNG S P. Stabilization of Timoshenko beam by means of pointwise controls[J]. ESAIM Control Optim Calc Var, 2003,9:579-600.

[5]AMMAR-KHODJA F, BENABDALLAH A, MUNOZ R J E, et al. Energy decay for Timoshenko systems of memory type[J]. J Differential Equations，2003 ,194(1): 82-115.

[6]GUESMIA A, MESSAOUDI S A. On the control of a viscoelastic damped Timoshenko-type system[J]. Appl Math Comput, 2008, 26(2):589-597.

[7]SANTOS M. Decay rates for solutions of a Timoshenko system with a memory condition at the boundary[J]. Abstr Appl Anal, 2002, 7 (10):531-546.

[8]MESSAOUDI S A, MUSTAFA M A. A stability result in a memory-type Timoshenko system[J]. Dynamic Systems Appl, 2009,18(3-4):457-468.

[9]MESSAOUDI S A, SAID-HOUARI B. Uniform decay in a Timoshenko-type system with past history[J]. J Math Anal Appl, 2009,360(2):459-475.

[10]RIVERA J E M, FERNANDEZ SARE H D. Stability of Timoshenko systems with past history[J]. J Math Anal Appl, 2008, 339(1):482-502.

[11] PARENTE A, MIRANDA M M, JUTUC L P S G. On local solution for a nonlinear Timoshenko system[C]//Proccedings of the 55° SBA. Uberlandia-MG: Federal University of Uberlandia, 2002:167-179.

[12] ARARUNA F D, BORGES J E S. Existence and boundary stabilization of the semilinear Mindlin-Timoshenko system[J]. Electron J Qual Theory Differ Equa, 2008,34:1-27.

[13] CHUESHOV I, LASIECKA I. Global attractors for Mindlin-Timoshenko plates and for their Kirchhoff limits[J]. Milan J Math, 2006,74:117-138.

[14] GORGI C, VEGNI F M. Uniform energy estimates for a semilinear evolution equation of the Mindlin-Timoshenko beam with memory[J]. Mathematical and Computer Modelling, 2004,39: 1005-1021.

[15] PEI P, RAMMAHA M A, TOUNDYKOV D. Global well-posedness and stability of semilinear Mindlin-Timoshenko systems[J]. J Math Anal Appl, 2014,418:535 - 568.

[16] LEVINE H A. Instability and nonexistence of global solutions to nonlinear wave equations of the formPutt=-Au+F(u)[J]. Trans Amer Math Soc, 1974,192:1-21.

[17] KORPUSOV O M. Blowup of solutions of strongly dissipative generalized Klein-Gordon equation[J]. Izvestiya Mathematics, 2013,77(2):325 - 353.

[18] WLOKA J. Partial Differential Equation[M]. London： Cambridge University Press, 1987:1-10.

Blow up for Mindlin-Timoshenko Beam Equation with Memory and Arbitrary Positive Initial Energy

YAN Deming1, ZHANG Guixia2

(1.SchoolofMathematicsandStatistics,HenanInstituteofEducation,Zhengzhou450046,China; 2.SanmenxiaHubinSecondaryVocationalSchool,Sanmenxia472002,China)

Abstract:Concerning one-dimensional Mindlin-Timoshenko model for beam with linear damping and memory terms. By the modified convexity method, a blow-up result for the solution to the Mindlin-Timoshenko system is obtained under arbitrary positive initial energy and appropriate initial datum.

Key words:Mindlin-Timoshenko beam equation; initial boundary value problem; memory；improved convexity method; blow up

中图分类号：O172.27

文献标志码：A

文章编号：1007-0834(2016)01-0001-05

doi：10.3969/j.issn.1007-0834.2016.01.001

作者简介：闫德明(1972—)，男，河南西华人，河南教育学院数学与统计学院副教授，博士，主要研究方向: 微分方程.

基金项目：河南省基础与前沿研究项目(1323004100360)

收稿日期：2015-11-09