关于拟严格伪压缩映像族的收缩投影方法

顾银鲁 , 马艳利

(银川能源学院 基础部,宁夏 银川 750105)



关于拟严格伪压缩映像族的收缩投影方法

顾银鲁 , 马艳利

(银川能源学院 基础部,宁夏 银川 750105)

摘要：在Hilbert空间中，引入和研究一种新的收缩投影方法，用逼近一族闭的拟严格伪压缩映像的公共不动点，并利用所提出的迭代方法证明了拟严格伪压缩映像族的不动公共点强收敛定理.

关键词：拟严格伪压缩映像族；不动点；收缩投影方法；闭映像

0引言

对于非扩张映像的不动点的迭代构造问题，数学家经过长期不断的努力和艰苦的深入研究以及探索，创造出了许多优秀成果[1-11]．本文将Hilbert空间中闭的拟严格伪压缩映像的收缩投影方法拓展到映像族上，给出一组新的迭代方法，然后对新的迭代方法对于强收敛于一点再加以证明.

1预备知识

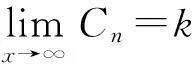
定义2[11]凸集：设z1,z2∈C，若tz1+(1-t)z2∈C,t∈(0,1),称C为凸集.

定义3[3]设H为Hilbert空间的内积，且C为H上的一个非空闭凸子集，设T:C→C的自映像，用F(T)表示T的不动点集.

定义4[2]映像T:C→C为拟严格伪压缩映像，当F(T)≠∅时，存在常数k∈[0,1)，对∀x∈C,y∈F(t)满足‖Tx-p‖2≤‖x-p‖2+k‖x-Tx‖2.

定义5[8]映像T:C→C为严格伪压缩映像，如果存在常数k∈[0,1)，对∀x,y∈C满足‖Tx-Ty‖2≤‖x-y‖2+k‖(I-T)x-(I-T)y‖2,也称T为k-严格伪压缩.

定义6[5]称映像T:C→C是非扩张映像，如果

‖Tx-Ty‖≤‖x-y‖,∀x,y∈C.

注1严格伪压缩映像包括非扩张映像，也就是说，T是非扩张映像，当且仅当T是0-严格伪压缩映像.

注2当F(T)≠∅时，所有的严格伪压缩映像都是拟严格伪压缩映像，然而其逆不真.

定义7[7]称映像f:C→C是压缩映像，如果存在常数k∈(0,1)，使得

‖fx-fy‖≤k‖x-y‖,∀x,y∈C.

范数具有下列性质[5]：

1)‖x‖≥0, 且‖x‖=0等价于x=0；

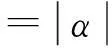
3)‖x+y‖≤‖x‖+‖y‖(范数不等式).

定义 8[10]设C为实Hilbert空间H中的非空闭凸子集，任意点x∈H，存在C中的一个点的邻域，记作PCx. 使得‖x-PCx‖≤‖x-y‖,对∀y∈C，称PCx为H到C的度量投影.

引理1[1]设C是实的Hilbert空间H中的一个非空闭凸子集，给定x∈H和z∈C,有z=PCx，当且仅当∀y∈C有〈x-z,y-z〉≤0 .

引理2[9]设C是Hilbert空间上的一个非空闭凸子集，映像PC:H→C，称为从H到C上的距离投影算子.

则有下面的式子成立，

‖y-PCx‖2+‖x-PCx‖2≤‖x-y‖2,∀x∈H,∀y∈C.

引理3[6]设H是一个Hilbert空间，有下列定义

1)‖x±y‖2=‖x‖2±2〈x,y〉+‖y‖2,∀x,y∈H;

2)‖tx+(1-t)y‖2=t‖x‖2+(1-t)‖y‖2-t(1-t)‖x-y‖2，其中t∈[0,1),∀x,y∈H.

显然由‖·‖的定义得

‖x-y‖2=‖x-z‖2+‖z-y‖2+2〈x-z,z-y〉，∀x,y,z∈H.

2主要结果

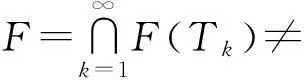
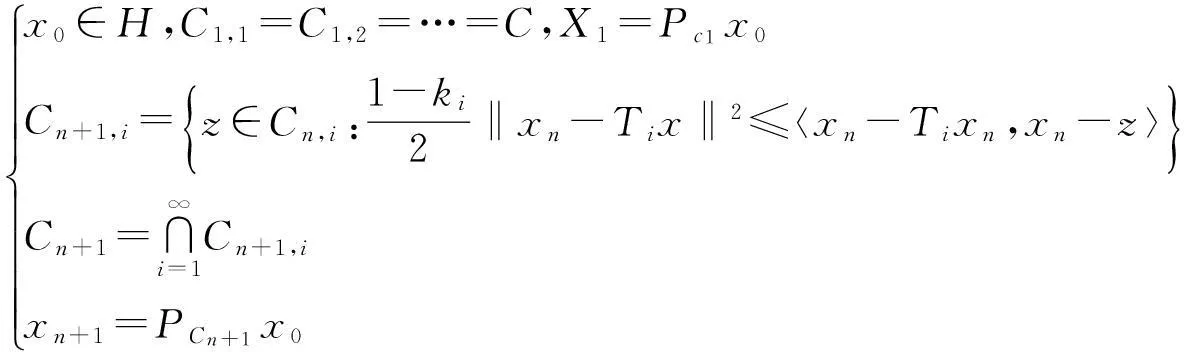
则数列{xn}强收敛于P0=PFx0.

证明以下分6步进行证明.

第1步：证明F是C的非空闭凸子集.

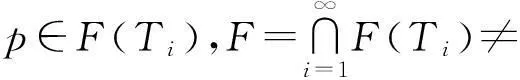
2)再证F是凸集. 先证对∀i∈N，F(Ti)是凸集.∀p1,p2∈F(Ti),t∈(0,1)，设pt=tp1+(1-t)p2，此时需要证明Tipt=pt. 因为 ‖p1-pt‖=(1-t)‖p1-p2‖

以及‖p2-pt‖=(1-t)‖p1-p2‖，由引理3的2)，有

‖pt-Tkpt‖2=‖t(p1-Tipt)+(1-t)(p2-Tipt)‖2=

t‖p1-Tipt‖2+(1-t)‖p2-Tipt‖2-t(1-t)‖p1-p2‖2≤

t(‖p1-pt‖2+ki‖pt-Tipt‖2)+(1-t)(‖p2-p1‖2+ki‖pt-Tipt‖2)-t(1-t)‖p1-p2‖2=

(t(1-t)2+(1-t)t2-t(1-t))‖p1-p2‖2+ki‖pt-Tipt‖2.

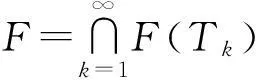
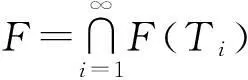
第2步：证明当n≥1时，Cn是一个闭凸集.

1)先证Cn,i是一个闭凸集.

①当n=1时，C1,1=C1,2=…=C是闭凸集.

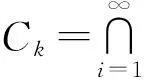
(i)首先证明Ck+1,i为闭集.

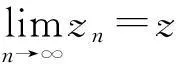
所以z∈Ck+1,i. 由闭集的定义可知Ck+1,i是闭集.

(ii)再证Ck+1,i是凸集.

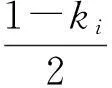
综上所述Ck+1,i是闭凸集，即所有的当n≥1时，都有Cn,i是闭凸集.

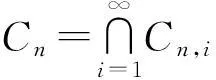
第3步：证明∀n≥1，有F⊂Cn.

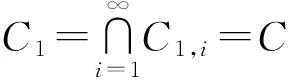
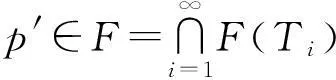
‖Tixk-p′‖2≤‖xk-p′‖2+k‖xk-Tixk‖2，

‖Tixk-xk‖2+‖xk-p′‖2+2〈Tixk-xk,xk-p′〉≤‖xk-p′‖2+k‖xk-Tixk‖2.

‖xn-x0‖2≤‖w-x0‖2-‖w-xn‖2≤‖w-x0‖2.

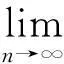
第5步：证明当n→∞,xn→p0. 由Cn的构造知，当m>n时，Cm⊂Cn和xm=PCmx0∈Cn,由引理2得

‖xm-xn‖2=‖xm-PCnx0‖2≤‖xm-x0‖2-‖PCnx0-x0‖2= ‖xm-x0‖2-‖xm-x0‖2.

两边同时取极限，当m,n→∞时，‖xm-xn‖→0，因此，序列{xn}是一个柯西列，所以当n→∞时，有xn→p0∈C.

第6步：证明p0=PFx0.

1)首先证明p0=TFx0. 由上一步已经得知，当n→∞时，x→p0(p0∈C)，因此，当n→∞时，‖xn+1-xn‖→0. 当xn+1∈Cn+1时，有

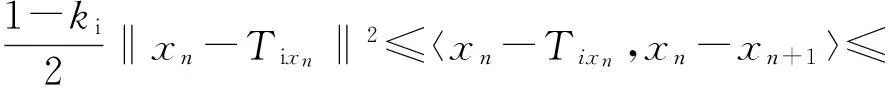
这就表明,n→∞时，有‖xn-Tixn‖→0，因此，当n→∞时，有xnc-p0∈C，从而有当n→∞时，Tkxn→p0∈C. 由Ti是闭集，则p0=pip0.

2)再证明p0=PFx0.由xn=PCnx0，可以得到，对任意y∈Cn，〈y-xn,x0-xn〉≤0，当F⊂Cn对任意n≥1，得到∀w∈F,有〈w-xn,x0-xn〉≤0，取极限，即当n→∞时，有〈w-p0,x0-p0〉≤0(∀w∈F)，从而由引理1可得p0=PFx0. 因此，定理1得证.

参考文献

[1]高兴慧，周海云. 拟φ-渐近非扩展映像族的公共不动点的迭代算法[J]. 系统科学与数学，2010，30(4): 486-492.

[2]高兴慧，马乐荣，周海云. Banach空间中拟φ-渐近非扩展映像不动点的迭代算法[J]. 数学的实践与认识，2009，39(9): 220-224.

[3]高兴慧，马乐荣，周海云. Hilbert空间中非扩张映像族公共不动点的存在性[J]. 云南大学学报(自然科学版)，2010，32(3): 249-253.

[4]高兴慧，马乐荣，周海云. 非扩张映像和非扩展映像公共不动点的强收敛定理[J]. 西南师范大学学报(自然科学版)，2010，35(3): 29-32.

[5]ZHOU HAIYUN，GAO XINGHUI. An iterative method of fixed points for closed and quasi-strict pseudo-contractions in Banach spaces[J]. Journal of Applied Mathematics and Computing, 2010, 33: 227-237.

[6]高兴慧，周海云. Strong convergence theorems for a family of quasi-φ-asympt-otically nonexpansive mappings [J]. 数学研究与评论，2011，31(2): 303-314.

[7]马乐荣，高兴慧，周海云. Banach空间中增生算子的粘滞逼近问题[J]. 西南师范大学学报(自然科学版)，2010，35(3): 33-36.

[8]马乐荣，高兴慧. K-严格伪压缩映像不动点的粘滞算法[J]. 延安大学学报(自然科学版)，2010，29(3): 21-23.

[9]周海云，马炳坤．Banach空间中可数-φ-非扩张映像族的公共不动点的收敛定理[J]．数学年刊，2010，31A(5):565-570．

[10]ROCKAFELLAR R T．On the maximal monotonicity of subdifferential mapping[J]．Pacific J Math，1970，33:209-216．

[11]呈其襄，张奠宙，魏国强，等.实变函数与泛函分析基础[M]. 北京：高等教育出版社，2003：77-123.

A Shrinking Projection Method on Common Fixed Point for a Family of Quasi-strict Pseudo-contraction Mapping

GU Yinlu, MA Yanli

(DepartmentofBasics,YinchuanEnergyCollege,Yinchuan750105,China)

Abstract:Propose a kind of new shrinking projection method for a family of quasi-strict pseudo-contraction mapping and prove a strong convergence theorem for closed and quasi-strict pseudo-contractions in a Hilbert space.The result improves and extends some recent relative results.

Key words:a family of quasi-strict pseudo-contraction mapping； fixed point； shrinking projection methods； closed mapping

中图分类号：O177.91

文献标志码：A

文章编号：1007-0834(2016)01-0006-04

doi：10.3969/j.issn.1007-0834.2016.01.002

作者简介：顾银鲁(1981—)，女，山东邹城人，银川能源学院基础部讲师.

基金项目：银川能源学院科研基金项目(2015-KY-Y-29)

收稿日期：2015-10-13